广东省中山市11-12学年高二上学期期末试题数学文
文档属性
| 名称 | 广东省中山市11-12学年高二上学期期末试题数学文 |  | |
| 格式 | zip | ||
| 文件大小 | 200.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-18 14:14:24 | ||
图片预览



文档简介
中山市高二级2011—2012学年度第一学期期末统一考试
数学试卷(文科)
本试卷满分150分. 考试用时120分钟.
注意事项:
1、答卷前,考生务必用2B铅笔在答题卡“考生号”处填涂考生号,用黑色字迹钢笔或签字笔将自己姓名、考生号、试室号、座位号填写在答题卡上。
2、选择题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上。
3、非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上. 如需改动,先划掉原来的答案,然后再写上新的答案. 不准使用铅笔和涂改液. 不按以上要求作答的答案无效.
4、考生必须保持答题卡的整洁. 考试结束,将答题卡交回,试卷不用上交。
5、不可以使用计算器。
一、选择题(本大题共10小题,每小题5分,共50分. 在每小题给出的四个备选项中,只有一项是符合题目要求的.)
1.抛物线的焦点坐标是
A. B. C. D.
2.已知是等比数列,,则公比q=
A.2 B. C. D.
3.已知△ABC的三内角A,B,C成等差数列,且AB=1,BC=4,则该三角形面积为
A. B.2 C.2 D.4
4.若,则以下命题为真的是
A.若,则 B.若,则
C.若,则 D.若,则
5. 函数在点(1,1)处的切线方程为
A. B.
C. D.
6.当在上变化时,导函数的符号变化如下表:
1 (1,4) 4
- 0 + 0 -
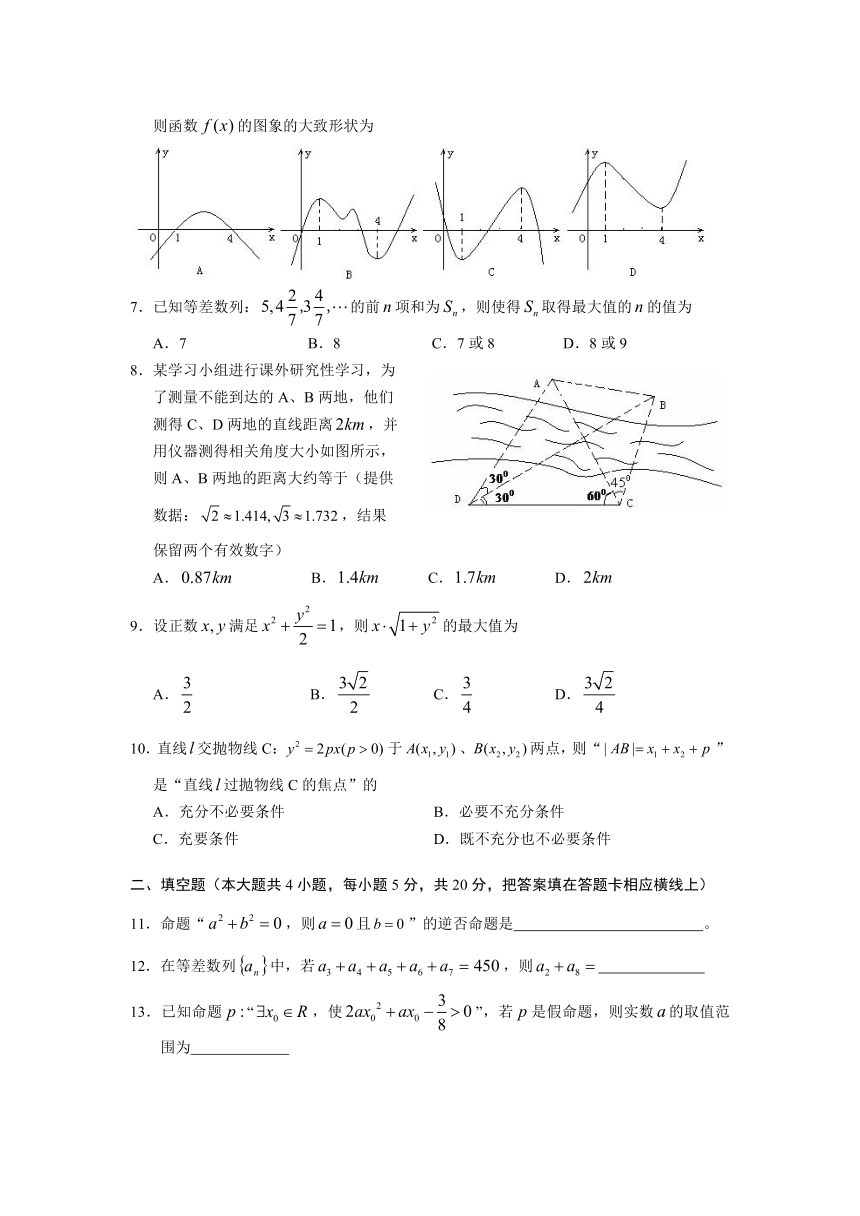
则函数的图象的大致形状为
7.已知等差数列:的前项和为,则使得取得最大值的的值为
A.7 B.8 C.7或8 D.8或9
8.某学习小组进行课外研究性学习,为
了测量不能到达的A、B两地,他们
测得C、D两地的直线距离,并
用仪器测得相关角度大小如图所示,
则A、B两地的距离大约等于(提供
数据:,结果
保留两个有效数字)
A. B. C. D.
9.设正数满足,则的最大值为
A. B. C. D.
10.直线交抛物线C:于、两点,则“”是“直线过抛物线C的焦点”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题卡相应横线上)
11.命题“,则且”的逆否命题是 。
12.在等差数列中,若,则
13.已知命题“,使”,若是假命题,则实数的取值范围为
14.关于双曲线,有以下说法:①实轴长为6;②双曲线的离心率是;③焦点坐标为;④渐近线方程是,⑤焦点到渐近线的距离等于3。正确的说法是 .(把所有正确的说法序号都填上)
三、解答题(本大题共6小题,共80分,解答须写出文字说明、证明过程和演算步骤.)
15.(本小题满分12分)在等比数列中,已知.
(1)求数列的通项;
(2)在等差数列中,若,求数列前项和.
16.(本小题满分12分)某村计划建造一个室内面积为
800m2的矩形蔬菜温室. 在温室内,种植蔬菜时需
要沿左、右两侧与前侧内墙各保留1m宽的空地作
为通道,后侧内墙不留空地(如图所示),问当温
室的长是多少米时,能使蔬菜的种植面积最大?
17.(本小题满分14分)△ABC的三个内角A、B、C所对边长分别为a、b、c,已知c=3,C=60°。(1)若A=75°,求b的值;(2)若a=2 b, 求b的值。
18.(本小题满分14分)已知函数(为实常数)。
(1)求的单调区间;(2)求在区间上的最大值与最小值.
19.(本小题满分14分)中山市某家电企业根据市场调查分析,决定调整新产品生产方案,准备每周(按40个工时计算)生产空调机、彩电、冰箱共120台,且冰箱至少生产20台,已知生产这些家电产品每台所需工时和每台产值如下表:
家电名称 空调机 彩电 冰箱
工时
产值/千元 4 3 2
问每周应生产空调机、彩电、冰箱各多少台,才能使产值最高?最高产值是多少?(以千元为单位)
20.(本小题满分14分)已知椭圆C的中心在原点,焦点在轴上,焦距为,且过点M。(1)求椭圆C的方程;(2)若过点的直线交椭圆C于A、B两点,且N恰好为AB中点,能否在椭圆C上找到点D,使△ABD的面积最大?若能,求出点D的坐标;若不能,请说明理由。
中山市高二级2011—2012学年度第一学期期末统一考试
数学试卷(文科)参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B B A D A C C B D C
二、填空题答案:
11.若,或,则
12.180
13.
14.②④⑤
三、解答题
15. 解:(1)由 ,得q=2,解得,从而. …………5分
(2)由已知得,又,解得d=-2. ………………8分
∴ ………………12分
16.解:设温室的长为xm,则宽为m(x>0), ………2分
所以可种植蔬菜的面积为
. ………6分
令,则. 由,得.
当为减函数,当为增函数.
∴ 当时,取得最小值,S(x)取得最大值.
答:温室的长为40m时,蔬菜的种植面积最大. ………12分
17.解:(1)由,得 …………………………2分
由正弦定理知, ……………………………………………3分
…………………………………………7分
(2)由余弦定理知, ……………………………9分
将代入上式得
……………………………………12分
……………………………………………………………………14分
18.解:(1) ……………………………1分
函数的定义域为
令,有,解之得 ………………3分
令,有,或 ………………4分
所以函数的单调区间为,。 ………………6分
[端点1包含与否,不扣分]
(2)当在上变化时,的变化情况如下表: ………10分
由表知,函数, ………12分
又,
,
,
所以. ………………………14分
19.解:设该企业每周应生产空调机台、彩电台,则应生产冰箱台,产值为(千元), ………………2分
所以满足约束条件
,
即…………………………………6分
可行域如右图………………………9分
联立方程组
,解得………………11分
将平移到过点时,取最大值,
(千元)……………………13分
答:每周应生产空调机10台,彩电90台,冰箱20台,才能使产值最高,最高产值是350千元。…………14分
20.解:(1)法一:依题意,设椭圆方程为,则 …………1分
, …………………………………………………………………2分
因为椭圆两个焦点为,所以
=4 ………4分
…………………………………………………………5分
椭圆C的方程为 ……………………………………………………6分
法二:依题意,设椭圆方程为,则 ………………………1分
,即,解之得 …………………5分
椭圆C的方程为…………………………………………………………6分
(2)法一:设A、B两点的坐标分别为,
则 ………………………7分
………………①
………………②
①-②,得
…………………………………………9分
设与直线AB平行且与椭圆相切的直线方程为
联立方程组,消去整理得
由判别式
得 …………………………12分
由图知,当时,与椭圆的切点为D,
此时△ABD的面积最大
所以D点的坐标为 ………………14分
法二:设直线AB的方程为,
联立方程组,消去整理得
设A、B两点的坐标分别为,则
所以直线AB的方程为,即……………9分
(以下同法一)
数学试卷(文科)
本试卷满分150分. 考试用时120分钟.
注意事项:
1、答卷前,考生务必用2B铅笔在答题卡“考生号”处填涂考生号,用黑色字迹钢笔或签字笔将自己姓名、考生号、试室号、座位号填写在答题卡上。
2、选择题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上。
3、非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上. 如需改动,先划掉原来的答案,然后再写上新的答案. 不准使用铅笔和涂改液. 不按以上要求作答的答案无效.
4、考生必须保持答题卡的整洁. 考试结束,将答题卡交回,试卷不用上交。
5、不可以使用计算器。
一、选择题(本大题共10小题,每小题5分,共50分. 在每小题给出的四个备选项中,只有一项是符合题目要求的.)
1.抛物线的焦点坐标是
A. B. C. D.
2.已知是等比数列,,则公比q=
A.2 B. C. D.
3.已知△ABC的三内角A,B,C成等差数列,且AB=1,BC=4,则该三角形面积为
A. B.2 C.2 D.4
4.若,则以下命题为真的是
A.若,则 B.若,则
C.若,则 D.若,则
5. 函数在点(1,1)处的切线方程为
A. B.
C. D.
6.当在上变化时,导函数的符号变化如下表:
1 (1,4) 4
- 0 + 0 -
则函数的图象的大致形状为
7.已知等差数列:的前项和为,则使得取得最大值的的值为
A.7 B.8 C.7或8 D.8或9
8.某学习小组进行课外研究性学习,为
了测量不能到达的A、B两地,他们
测得C、D两地的直线距离,并
用仪器测得相关角度大小如图所示,
则A、B两地的距离大约等于(提供
数据:,结果
保留两个有效数字)
A. B. C. D.
9.设正数满足,则的最大值为
A. B. C. D.
10.直线交抛物线C:于、两点,则“”是“直线过抛物线C的焦点”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题卡相应横线上)
11.命题“,则且”的逆否命题是 。
12.在等差数列中,若,则
13.已知命题“,使”,若是假命题,则实数的取值范围为
14.关于双曲线,有以下说法:①实轴长为6;②双曲线的离心率是;③焦点坐标为;④渐近线方程是,⑤焦点到渐近线的距离等于3。正确的说法是 .(把所有正确的说法序号都填上)
三、解答题(本大题共6小题,共80分,解答须写出文字说明、证明过程和演算步骤.)
15.(本小题满分12分)在等比数列中,已知.
(1)求数列的通项;
(2)在等差数列中,若,求数列前项和.
16.(本小题满分12分)某村计划建造一个室内面积为
800m2的矩形蔬菜温室. 在温室内,种植蔬菜时需
要沿左、右两侧与前侧内墙各保留1m宽的空地作
为通道,后侧内墙不留空地(如图所示),问当温
室的长是多少米时,能使蔬菜的种植面积最大?
17.(本小题满分14分)△ABC的三个内角A、B、C所对边长分别为a、b、c,已知c=3,C=60°。(1)若A=75°,求b的值;(2)若a=2 b, 求b的值。
18.(本小题满分14分)已知函数(为实常数)。
(1)求的单调区间;(2)求在区间上的最大值与最小值.
19.(本小题满分14分)中山市某家电企业根据市场调查分析,决定调整新产品生产方案,准备每周(按40个工时计算)生产空调机、彩电、冰箱共120台,且冰箱至少生产20台,已知生产这些家电产品每台所需工时和每台产值如下表:
家电名称 空调机 彩电 冰箱
工时
产值/千元 4 3 2
问每周应生产空调机、彩电、冰箱各多少台,才能使产值最高?最高产值是多少?(以千元为单位)
20.(本小题满分14分)已知椭圆C的中心在原点,焦点在轴上,焦距为,且过点M。(1)求椭圆C的方程;(2)若过点的直线交椭圆C于A、B两点,且N恰好为AB中点,能否在椭圆C上找到点D,使△ABD的面积最大?若能,求出点D的坐标;若不能,请说明理由。
中山市高二级2011—2012学年度第一学期期末统一考试
数学试卷(文科)参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B B A D A C C B D C
二、填空题答案:
11.若,或,则
12.180
13.
14.②④⑤
三、解答题
15. 解:(1)由 ,得q=2,解得,从而. …………5分
(2)由已知得,又,解得d=-2. ………………8分
∴ ………………12分
16.解:设温室的长为xm,则宽为m(x>0), ………2分
所以可种植蔬菜的面积为
. ………6分
令,则. 由,得.
当为减函数,当为增函数.
∴ 当时,取得最小值,S(x)取得最大值.
答:温室的长为40m时,蔬菜的种植面积最大. ………12分
17.解:(1)由,得 …………………………2分
由正弦定理知, ……………………………………………3分
…………………………………………7分
(2)由余弦定理知, ……………………………9分
将代入上式得
……………………………………12分
……………………………………………………………………14分
18.解:(1) ……………………………1分
函数的定义域为
令,有,解之得 ………………3分
令,有,或 ………………4分
所以函数的单调区间为,。 ………………6分
[端点1包含与否,不扣分]
(2)当在上变化时,的变化情况如下表: ………10分
由表知,函数, ………12分
又,
,
,
所以. ………………………14分
19.解:设该企业每周应生产空调机台、彩电台,则应生产冰箱台,产值为(千元), ………………2分
所以满足约束条件
,
即…………………………………6分
可行域如右图………………………9分
联立方程组
,解得………………11分
将平移到过点时,取最大值,
(千元)……………………13分
答:每周应生产空调机10台,彩电90台,冰箱20台,才能使产值最高,最高产值是350千元。…………14分
20.解:(1)法一:依题意,设椭圆方程为,则 …………1分
, …………………………………………………………………2分
因为椭圆两个焦点为,所以
=4 ………4分
…………………………………………………………5分
椭圆C的方程为 ……………………………………………………6分
法二:依题意,设椭圆方程为,则 ………………………1分
,即,解之得 …………………5分
椭圆C的方程为…………………………………………………………6分
(2)法一:设A、B两点的坐标分别为,
则 ………………………7分
………………①
………………②
①-②,得
…………………………………………9分
设与直线AB平行且与椭圆相切的直线方程为
联立方程组,消去整理得
由判别式
得 …………………………12分
由图知,当时,与椭圆的切点为D,
此时△ABD的面积最大
所以D点的坐标为 ………………14分
法二:设直线AB的方程为,
联立方程组,消去整理得
设A、B两点的坐标分别为,则
所以直线AB的方程为,即……………9分
(以下同法一)
同课章节目录
