广东省中山市2012届高三上学期期末试题数学理
文档属性
| 名称 | 广东省中山市2012届高三上学期期末试题数学理 |  | |
| 格式 | zip | ||
| 文件大小 | 231.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-18 14:14:42 | ||
图片预览



文档简介
中山市高三级2011—2012学年度第一学期期末统一考试
数学试卷(理科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试用时120分钟.
注意事项:
1、答第I卷前,考生务必将自己的姓名、统考考号、座位号、考试科目用铅笔涂写在答题卡上。
2、每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题上。
3、不可以使用计算器。
4、考试结束,将答题卡交回,试卷不用上交。
第Ⅰ卷(选择题共40分)
一、选择题:(本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知角的终边在第二象限,则的终边所在的象限为
A.第一或第二象限 B.第一或第三象限 C.第二或第四象限 D.第一或第四象限
2.设m,n是两条不同直线,是两个不同的平面,给出下列四个命题
①若
②
③若
④若
其中正确的命题是
A.① B.② C.③④ D.②④
3.已知的值为
A. B. C. D.
4. 如程序框图:若输入,,则输出
A.0 B.3 C.6 D.12
5.已知变量的最大值为
A.2 B. C. D.1
6.若是等差数列,首项,,则使前n项和成立的最大正整数n是
A.2011 B.2012 C.4022 D.4023
7.假如北京大学给中山市某三所重点中学7个自主招生的推荐名额,则每所中学至少分到一个名额的方法数为
A.10 B.15 C.21 D.30
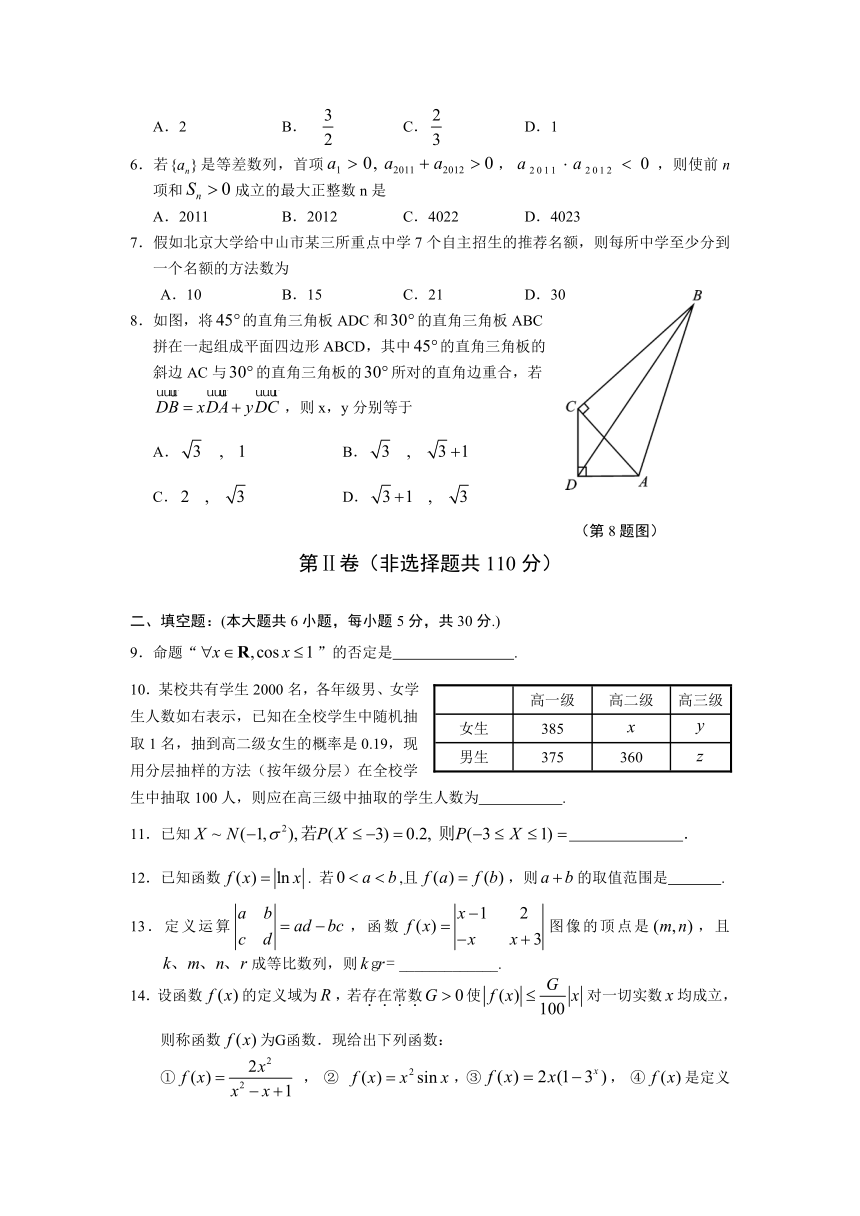
8.如图,将的直角三角板ADC和的直角三角板ABC
拼在一起组成平面四边形ABCD,其中的直角三角板的
斜边AC与的直角三角板的所对的直角边重合,若
,则x,y分别等于
A. B.
C. D.
(第8题图)
第Ⅱ卷(非选择题共110分)
二、填空题:(本大题共6小题,每小题5分,共30分.)
9.命题“”的否定是 .
高一级 高二级 高三级
女生 385
男生 375 360
10.某校共有学生2000名,各年级男、女学生人数如右表示,已知在全校学生中随机抽取1名,抽到高二级女生的概率是0.19,现用分层抽样的方法(按年级分层)在全校学生中抽取100人,则应在高三级中抽取的学生人数为 .
11.已知 .
12.已知函数. 若,且,则的取值范围是 .
13.定义运算,函数图像的顶点是,且成等比数列,则_____________.
14.设函数的定义域为,若存在常数使对一切实数均成立,则称函数为G函数.现给出下列函数:
① , ② ,③, ④是定义在的奇函数,且对一切,恒有.则其中是函数的序号为____________.
三、解答题:(本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.)
15.(本小题满分12分)
在△ABC中,a、b、c分别是角A、B、C所对的边,满足
(1)求角B的大小;
(2)若,求函数的值域。
16.(本小题满分12分)
我市某大学组建了A、B、C、D、E五个不同的社团组织,为培养学生的兴趣爱好,要求每个学生必须参加且只能参加一个社团,假定某寝室的甲、乙、丙三名学生对这五个社团的选择是等可能的。 (1)求甲、乙、丙三名学生中至少有两人参加同一社团的概率;
(2)设随机变量为甲、乙、丙这三个学生参加A或B社团的人数,求的分布列与数学期望。
17.(本小题满分14分)
如图,是以为直角的三角形,平面ABC,
SA=BC=2,AB= 4. M、N、D分别是SC、AB、BC的中点。
(1)求证:MNAB;
(2)求二面角S—ND—A的余弦值;
(3)求点A到平面SND的距离。
18.(本小题满分14分)
已知数列{}的前n项和为,满足
(1)证明:数列{+ 2}是等比数列.并求数列{}的通项公式;
(2)若数列{}满足,设是数列的前n项和.
求证:.
19.(本小题满分14分)
大闸蟹味道鲜美,主要产于太湖流域,在自然状态下它是一种可再生资源,为持续利用这一资源,需从宏观上考察其再生能力及捕捞强度对蟹群总量的影响。用xn表示某蟹群在第n年年初的总量,n∈N*,且x1>0.不考虑其它因素,设在第n年内蟹群的繁殖量及捕捞量都与xn成正比,死亡量与 成正比,这些比例系数依次为正常数a,b,c.
(1)试用xn表示成xn+1的函数;
(2)猜想:当且仅当x1,a,b,c满足什么条件时,每年年初蟹群的总量保持不变?(不要求证明)
(3)设a=2,c=1,为保证对任意x1∈(0,2),都有xn>0,n∈N*,则捕捞强度b的最大允许值是多少?证明你的结论。
20.(本小题满分14分)已知函数
(1)求函数的单调区间;
(2)若恒成立,试确定实数k的取值范围;
(3)证明:
①上恒成立
②
中山市高三级2011—2012学年度第一学期期末统一考试
数学试卷(理科)答案
一、选择题 BDBCB CBB
二、填空题
9.; 10. 25; 11.0.6; 12.; 13.; 14. ①④.
三、解答题
15.(本小题满分12分)
甲、乙、丙这三个学生每人参加A或B社团的概率都是,所以分布列为……10分
由此期望 ………12分
17. (本小题满分12分)
(1)略证:作MEAC, 连接NE,可证得AB平面MNE,即得MNAB …………4分
解法二:(向量法) B为坐标原点,建立空间直角坐标系(如图)
由题意得M(1,2,1),N(0,2,0)
…………4分
(2)
…………7分
…………10分
(3) …………14分
18 (本小题满分14分)
证明:(1)由 得 Sn=2an-2n
当n∈N*时,Sn=2an-2n,① 当n=1 时,S1=2a1-2,则a1=2,………1分
则当n≥2, n∈N*时,Sn-1=2an-1-2(n-1). ②
①-②,得an=2an-2an-1-2,
即an=2an-1+2,………………………2分
∴an+2=2(an-1+2)
∴………………………4分
∴ {an+2}是以a1+2为首项,以2为公比的等比数列. ………………………5分
∴an+2=4·2n-1,
∴an=2n+1-2,…………………………………6分
(2)证明:由 ………7分
则 ③
④…………………9分
③-④,得
………………13分
所以 ………………14分
19. (本小题满分14分)
19.解(1)从第n年初到第n+1年初,蟹群的繁殖量为axn,被捕捞量为bxn,死亡量为
……(4分)
(2)若每年年初蟹群总量保持不变,则xn恒等于x1, n∈N*,即从而由(*)式得
因为x1>0,所以a>b.
猜测:当且仅当a>b,且时,每年年初蟹群的总量保持不变.…(8分)
(3)若要b的值使得xn>0,n∈N*
由xn+1=xn(3-b-xn), n∈N*, 知
0而x1∈(0, 2),所以
由此猜测b的最大允许值是1. ……(10分)
下证(数学归纳法):当x1∈(0, 2) ,b=1时,都有xn∈(0, 2), n∈N*
①当n=1时,结论显然成立.
②假设当n=k时结论成立,即xk∈(0, 2), ………(11分)
则当n=k+1时,xk+1=xk(2-xk)>0.又因为xk+1=xk(2-xk)=-(xk-1)2+1≤1<2,
所以xk+1∈(0, 2),故当n=k+1时结论也成立. ………(13分)
由①、②可知,对于任意的n∈N*,都有xn∈(0,2).
综上所述,为保证对任意x1∈(0, 2), 都有xn>0,n∈N*,则捕捞强度b的最大允许值是1.
………………………………(14分)
20. (本小题满分14分)
解:(1)函数 …………………(1分)
当时,则上是增函数 ………(2分)
当时,若时有 ………(3分)
若时有则上是增函数,
在上是减函数……………………(5分)
(2)解法一:由(I)知,时递增,而不成立,故 ……………………………………(7分)
又由(I)知,要使恒成立,
则即可。 由……………(9分)
解法二(分离变量法):
………………(9分)
(3)①证明;由(2)知,当时有恒成立,且上是减函数,,恒成立,即上恒成立 。 ……………………(11分)
②证明:令,则,即,从而,
成立
………………(14分)
开始
是
输出n
结束
输入m,n
m=n
n = r
r =0
否
(第4题)
y
z
数学试卷(理科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试用时120分钟.
注意事项:
1、答第I卷前,考生务必将自己的姓名、统考考号、座位号、考试科目用铅笔涂写在答题卡上。
2、每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题上。
3、不可以使用计算器。
4、考试结束,将答题卡交回,试卷不用上交。
第Ⅰ卷(选择题共40分)
一、选择题:(本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知角的终边在第二象限,则的终边所在的象限为
A.第一或第二象限 B.第一或第三象限 C.第二或第四象限 D.第一或第四象限
2.设m,n是两条不同直线,是两个不同的平面,给出下列四个命题
①若
②
③若
④若
其中正确的命题是
A.① B.② C.③④ D.②④
3.已知的值为
A. B. C. D.
4. 如程序框图:若输入,,则输出
A.0 B.3 C.6 D.12
5.已知变量的最大值为
A.2 B. C. D.1
6.若是等差数列,首项,,则使前n项和成立的最大正整数n是
A.2011 B.2012 C.4022 D.4023
7.假如北京大学给中山市某三所重点中学7个自主招生的推荐名额,则每所中学至少分到一个名额的方法数为
A.10 B.15 C.21 D.30
8.如图,将的直角三角板ADC和的直角三角板ABC
拼在一起组成平面四边形ABCD,其中的直角三角板的
斜边AC与的直角三角板的所对的直角边重合,若
,则x,y分别等于
A. B.
C. D.
(第8题图)
第Ⅱ卷(非选择题共110分)
二、填空题:(本大题共6小题,每小题5分,共30分.)
9.命题“”的否定是 .
高一级 高二级 高三级
女生 385
男生 375 360
10.某校共有学生2000名,各年级男、女学生人数如右表示,已知在全校学生中随机抽取1名,抽到高二级女生的概率是0.19,现用分层抽样的方法(按年级分层)在全校学生中抽取100人,则应在高三级中抽取的学生人数为 .
11.已知 .
12.已知函数. 若,且,则的取值范围是 .
13.定义运算,函数图像的顶点是,且成等比数列,则_____________.
14.设函数的定义域为,若存在常数使对一切实数均成立,则称函数为G函数.现给出下列函数:
① , ② ,③, ④是定义在的奇函数,且对一切,恒有.则其中是函数的序号为____________.
三、解答题:(本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.)
15.(本小题满分12分)
在△ABC中,a、b、c分别是角A、B、C所对的边,满足
(1)求角B的大小;
(2)若,求函数的值域。
16.(本小题满分12分)
我市某大学组建了A、B、C、D、E五个不同的社团组织,为培养学生的兴趣爱好,要求每个学生必须参加且只能参加一个社团,假定某寝室的甲、乙、丙三名学生对这五个社团的选择是等可能的。 (1)求甲、乙、丙三名学生中至少有两人参加同一社团的概率;
(2)设随机变量为甲、乙、丙这三个学生参加A或B社团的人数,求的分布列与数学期望。
17.(本小题满分14分)
如图,是以为直角的三角形,平面ABC,
SA=BC=2,AB= 4. M、N、D分别是SC、AB、BC的中点。
(1)求证:MNAB;
(2)求二面角S—ND—A的余弦值;
(3)求点A到平面SND的距离。
18.(本小题满分14分)
已知数列{}的前n项和为,满足
(1)证明:数列{+ 2}是等比数列.并求数列{}的通项公式;
(2)若数列{}满足,设是数列的前n项和.
求证:.
19.(本小题满分14分)
大闸蟹味道鲜美,主要产于太湖流域,在自然状态下它是一种可再生资源,为持续利用这一资源,需从宏观上考察其再生能力及捕捞强度对蟹群总量的影响。用xn表示某蟹群在第n年年初的总量,n∈N*,且x1>0.不考虑其它因素,设在第n年内蟹群的繁殖量及捕捞量都与xn成正比,死亡量与 成正比,这些比例系数依次为正常数a,b,c.
(1)试用xn表示成xn+1的函数;
(2)猜想:当且仅当x1,a,b,c满足什么条件时,每年年初蟹群的总量保持不变?(不要求证明)
(3)设a=2,c=1,为保证对任意x1∈(0,2),都有xn>0,n∈N*,则捕捞强度b的最大允许值是多少?证明你的结论。
20.(本小题满分14分)已知函数
(1)求函数的单调区间;
(2)若恒成立,试确定实数k的取值范围;
(3)证明:
①上恒成立
②
中山市高三级2011—2012学年度第一学期期末统一考试
数学试卷(理科)答案
一、选择题 BDBCB CBB
二、填空题
9.; 10. 25; 11.0.6; 12.; 13.; 14. ①④.
三、解答题
15.(本小题满分12分)
甲、乙、丙这三个学生每人参加A或B社团的概率都是,所以分布列为……10分
由此期望 ………12分
17. (本小题满分12分)
(1)略证:作MEAC, 连接NE,可证得AB平面MNE,即得MNAB …………4分
解法二:(向量法) B为坐标原点,建立空间直角坐标系(如图)
由题意得M(1,2,1),N(0,2,0)
…………4分
(2)
…………7分
…………10分
(3) …………14分
18 (本小题满分14分)
证明:(1)由 得 Sn=2an-2n
当n∈N*时,Sn=2an-2n,① 当n=1 时,S1=2a1-2,则a1=2,………1分
则当n≥2, n∈N*时,Sn-1=2an-1-2(n-1). ②
①-②,得an=2an-2an-1-2,
即an=2an-1+2,………………………2分
∴an+2=2(an-1+2)
∴………………………4分
∴ {an+2}是以a1+2为首项,以2为公比的等比数列. ………………………5分
∴an+2=4·2n-1,
∴an=2n+1-2,…………………………………6分
(2)证明:由 ………7分
则 ③
④…………………9分
③-④,得
………………13分
所以 ………………14分
19. (本小题满分14分)
19.解(1)从第n年初到第n+1年初,蟹群的繁殖量为axn,被捕捞量为bxn,死亡量为
……(4分)
(2)若每年年初蟹群总量保持不变,则xn恒等于x1, n∈N*,即从而由(*)式得
因为x1>0,所以a>b.
猜测:当且仅当a>b,且时,每年年初蟹群的总量保持不变.…(8分)
(3)若要b的值使得xn>0,n∈N*
由xn+1=xn(3-b-xn), n∈N*, 知
0
由此猜测b的最大允许值是1. ……(10分)
下证(数学归纳法):当x1∈(0, 2) ,b=1时,都有xn∈(0, 2), n∈N*
①当n=1时,结论显然成立.
②假设当n=k时结论成立,即xk∈(0, 2), ………(11分)
则当n=k+1时,xk+1=xk(2-xk)>0.又因为xk+1=xk(2-xk)=-(xk-1)2+1≤1<2,
所以xk+1∈(0, 2),故当n=k+1时结论也成立. ………(13分)
由①、②可知,对于任意的n∈N*,都有xn∈(0,2).
综上所述,为保证对任意x1∈(0, 2), 都有xn>0,n∈N*,则捕捞强度b的最大允许值是1.
………………………………(14分)
20. (本小题满分14分)
解:(1)函数 …………………(1分)
当时,则上是增函数 ………(2分)
当时,若时有 ………(3分)
若时有则上是增函数,
在上是减函数……………………(5分)
(2)解法一:由(I)知,时递增,而不成立,故 ……………………………………(7分)
又由(I)知,要使恒成立,
则即可。 由……………(9分)
解法二(分离变量法):
………………(9分)
(3)①证明;由(2)知,当时有恒成立,且上是减函数,,恒成立,即上恒成立 。 ……………………(11分)
②证明:令,则,即,从而,
成立
………………(14分)
开始
是
输出n
结束
输入m,n
m=n
n = r
r =0
否
(第4题)
y
z
同课章节目录
