小学数学苏教版六年级下册四 比例比和比例整理与复习(27张PPT)
文档属性
| 名称 | 小学数学苏教版六年级下册四 比例比和比例整理与复习(27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 16:11:00 | ||
图片预览



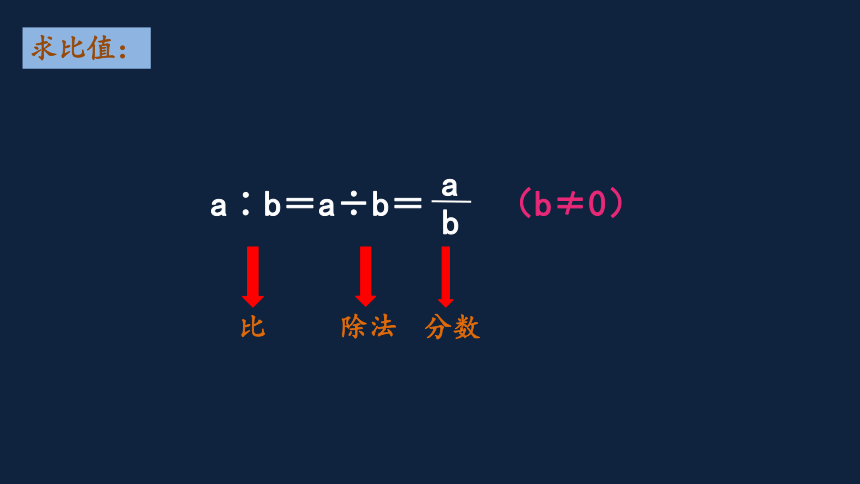



文档简介
比与比例整理与复习(1)
苏教版六年级下册 数学
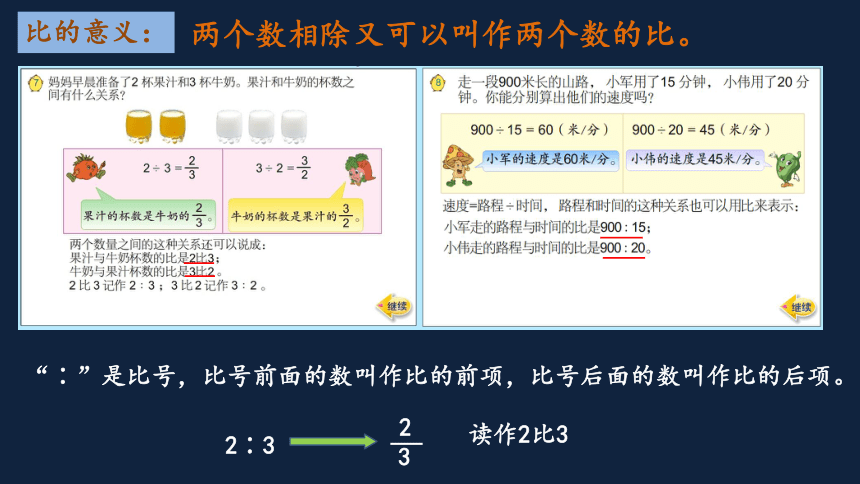
比
比的意义:
比的意义:
两个数相除又可以叫作两个数的比。
“∶”是比号,比号前面的数叫作比的前项,比号后面的数叫作比的后项。
2∶3
3
2
读作2比3
比
比的意义:
两个数相除又可以叫作两个数的比。
求比值:
比的前项除以后项所得的商。
求比值:
比
除法
分数
a∶b=a÷b= (b≠0)
b
a
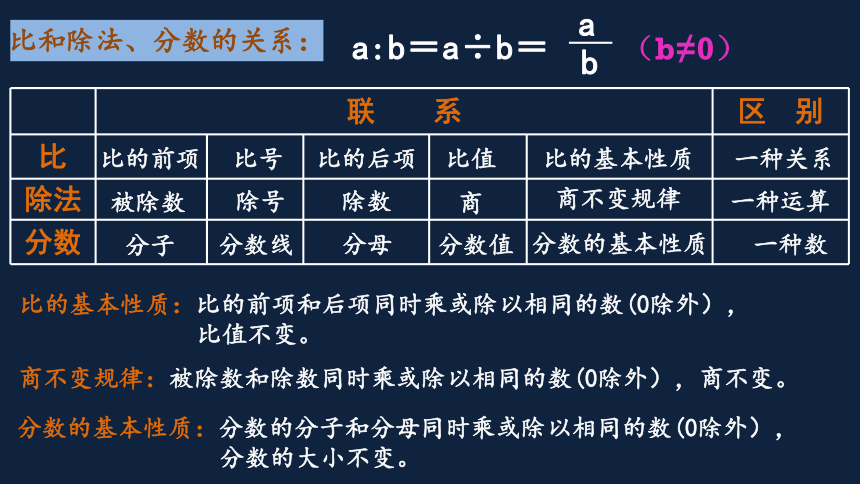
比和除法、分数的关系:
a:b=a÷b= (b≠0)
b
a
联 系
区 别
比
除法
分数
比的前项
比号
比的后项
比值
被除数
除号
除数
商
分子
分数线
分母
分数值
一种关系
一种数
一种运算
商不变规律:被除数和除数同时乘或除以相同的数(0除外),商不变。
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),
分数的大小不变。
比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),
比值不变。
比的基本性质
商不变规律
分数的基本性质
比
比的意义:
比的基本性质:
比和除法、分数的关系:
求比值:
两个数相除又可以叫作两个数的比。
比的前项除以后项所得的商。
a:b=a÷b= (b≠0)
b
a
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
化简比:
把两个数的比化成最简整数比。
(比的前项与后项互质)
化简比的一般方法:
=(12÷6)∶(18÷6)
12∶18
=2∶3
6
5
4
3
∶
=( ×12)∶( ×12)
6
5
4
3
=10∶9
1.8∶0.09
=(1.8×100)∶(0.09×100)
=180∶9
=20∶1
整数比
比的前项和后项同时除以它们的最大公因数
最简整数比
分数比
比的前项和后项同时乘分母的最小公倍数
小数比
比的前项和后项同时乘十、一百、一千……
依 据
结 果
求比值
化简比
比的意义
(前项÷后项)
一个数
一个比
比的基本性质
(化成最简整数比)
求比值与化简比的区别
比
比的意义:
比的基本性质:
比和除法、分数的关系:
求比值:
两个数相除又可以叫作两个数的比。
比的前项除以后项所得的商。
a:b=a÷b= (b≠0)
b
a
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
化简比:
把两个数的比化成最简单的整数比。
(比的前项与后项互质)
1.(1)六年级一班有男生23 人,女生24 人。男、女生人数的
比是( ), 女生与全班人数的比是( )。
(2)一辆汽车5小时行驶 240千米。这辆汽车行驶的路程与时
间的比是( ),行驶的时间与路程的比是( )。
(3)配制一种盐水,盐和水质量的比是 1︰24, 盐和盐水质
量的比是( ),水和盐水质量的比是( )。
23︰24
24︰47
48︰1
1︰48
1︰25
24︰25
(4)公鸡与母鸡只数的比是3︰7 ,公鸡占总只数的 ,
母鸡占总只数的 。
( )
( )
7
10
( )
( )
3
10
2.一个房间的地面由两种颜色的地砖铺成。
(1)写出两种地砖铺地面积的比,并化简。
地砖块数的比
20∶40=1∶2
(2)如果这个房间的面积是15平方米,两种地砖的铺地面积分别是多少平方米?
15÷(1+2)=5(平方米)
深色:5×1=5(平方米)
浅色:5×2=10(平方米)
深色:15× =5(平方米)
——
1
1+2
浅色:15× =10(平方米)
——
2
1+2
答:深色地砖的铺底面积是5平方米,
浅色地砖的铺底面积是10平方米。
答:深色地砖的铺底面积是5平方米,
浅色地砖的铺底面积是10平方米。
比例
比例的意义:
表示两个比相等的式子叫作比例。
2.
(1)量出每幅图片的长和宽, 并写出长和宽的比。
3.9︰2.7
2.6︰0.8
1.7︰1.7
1.3︰0.9
(2)先估计哪两个比能组成比例,再算一算,看估计得对不对。
2.
(2)先估计哪两个比能组成比例,再算一算,看估计得对不对。
3.9︰2.7=1.3︰0.9
答:第一幅图片和第四幅图片的比能组成比例。
比例
比例的意义:
比例的基本性质:
表示两个比相等的式子叫作比例。
在比例里,两个外项的积等于两个内项的积。
应用比例的基本性质,判断下面每组的两个比能否组成比例。如果能组成比例,把组成的比例写出来。
3.6∶1.8 和 0.5∶0.25
∶ 和18∶24
3.6×0.25=0.9
1.8×0.5=0.9
3.6∶1.8 = 0.5∶0.25
×24=8
×18=
不能组成比例
1
3
——
1
3
——
1
4
——
1
4
——
9
2
——
比例
比例的意义:
解比例:
比例的基本性质:
表示两个比相等的式子叫作比例。
在比例里,两个外项的积等于两个内项的积。
利用比例的基本性质求比例中的未知项。
3. 解比例。
9︰5 = 4.5︰x
︰x = ︰
解:9x = 5×4.5
9x = 22.5
x = 2.5
解:0.4x = 28×0.1
0.4x = 2.8
x = 7
解: x = ×
x =
x =
=
28
x
0.4
0.1
1
10
1
8
1
4
1
8
1
10
1
4
1
8
1
40
1
5
比例
比例的意义:
解比例:
比例的基本性质:
表示两个比相等的式子叫作比例。
在比例里,两个外项的积等于两个内项的积。
利用比例的基本性质求比例中的未知项。
比例尺:
图上距离∶实际距离=比例尺
6.分别量出学校到市民广场、少年宫、体育场和火车站的图上
距离,再根据比例尺算出它们的实际距离。
3cm
4cm
6cm
3cm
解:设学校到体育场的距离是x厘米。
600米=60000厘米
3∶x=1:60000
x=3×60000
x=180000
180000厘米=1800米
答:学校到体育场的实际距离是1800米。
6.分别量出学校到市民广场、少年宫、体育场和火车站的图上
距离,再根据比例尺算出它们的实际距离。
3cm
4cm
6cm
3cm
600×3=1800(米) 600×4=2400(米) 600×6=3600(米)
答:学校到市民广场的实际距离是1800米,到少年宫的实际距离是2400
米,到体育场的实际距离是1800米,到火车站的实际距离是3600米。
比例
比例的意义:
解比例:
比例的基本性质:
表示两个比相等的式子叫作比例。
在比例里,两个外项的积等于两个内项的积。
利用比例的基本性质求比例中的未知项。
比例尺:
图上距离∶实际距离=比例尺
正比例、反比例:
= k (一定)
y
x
x×y=k(一定)
比例
比例的意义:
解比例:
比例的基本性质:
表示两个比相等的式子叫作比例。
在比例里,两个外项的积等于两个内
项的积。
利用比例的基本性质求比例中的未知项。
比例尺:
图上距离∶实际距离=比例尺
正比例和反比例:
=k(一定)
x
y
x×y=k(一定)
a:b=a÷b= (b≠0)
比的前项和后项同时乘或除以相同的数
(0除外),比值不变。
比
比的意义:
比的基本性质:
比和除法、分数的关系:
求比值:
两个数相除又可以叫作两个数的比。
比的前项除以后项所得的商。
b
a
化简比:
把两个数的比化成最简单的整数比。
(比的前项与后项互质)
比 与
比
例的区别
意义不同
比的意义
两个数相除又叫做两个数的比。
比例的意义
表示两个比相等的式子叫做比例。
名称不同
比的各部分名称
比有两个项。比号前面的数叫做比的前项,比号后面的数叫做比的后项。
比例的各部分名称
比例有四个项。组成比例的四个数叫做比例的项,两端的两项叫做比例的的外项,中间的两项叫做比例的内项。
性质不同
比的基本性质
比的前项和后项同时乘或者除以相同的数(0除外),比值不变。
比例的基本性质
在比例里,两个外项的积等于两个内项的积。
应用不同
应用比的意义
求比值。
应用比的性质
化简比。
应用比例的意义
判断两个不能否组成比例。
应用比例的性质
不但可以判断两个比能否组成比例,还可以解比例。
《比和比例的整理与复习》自主练习
一、判断题
1、在比例里,两个外项的积与两个内项积的差是0。( )
2、任意两圆各自的周长和直径的比都可以组成比例。( )
3、一个60°的角,按1︰10的比例尺画在图纸上,图纸上的角
是6°。( )
4、在一个比例里,两个外项互为倒数,其中一个内项是5,另一个
内项是 。( )
5、10∶3=25∶x,求出x的值为20。( )
—
1
5
二、选择题:
1、方程12∶x=5∶3的解为( )。
A、x= B、x=20 C、x=0.8 D、x=
2、一个长方形,长是12厘米,宽是6厘米。
按一定比放大后,长是36厘米,宽是18厘米,它是按( )的比放大的。
按一定比缩小后,长是6厘米,宽是3厘米,它是按( )的比缩小的。
A、2∶1 B、1∶2 C、 3∶1 D、1∶3
3、如果A:5=9:B,那么AB=(? ?)。
A、5 B、9 C、45 D、1
4、在比例尺是1︰20的图纸上,甲、乙两个圆的直径的比是1︰8,那么甲、乙两个
圆的实际直径比是( )。
A、1︰8 B、1︰24 C、3︰8 D、1︰3
—
36
5
—
5
4
苏教版六年级下册 数学
比
比的意义:
比的意义:
两个数相除又可以叫作两个数的比。
“∶”是比号,比号前面的数叫作比的前项,比号后面的数叫作比的后项。
2∶3
3
2
读作2比3
比
比的意义:
两个数相除又可以叫作两个数的比。
求比值:
比的前项除以后项所得的商。
求比值:
比
除法
分数
a∶b=a÷b= (b≠0)
b
a
比和除法、分数的关系:
a:b=a÷b= (b≠0)
b
a
联 系
区 别
比
除法
分数
比的前项
比号
比的后项
比值
被除数
除号
除数
商
分子
分数线
分母
分数值
一种关系
一种数
一种运算
商不变规律:被除数和除数同时乘或除以相同的数(0除外),商不变。
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),
分数的大小不变。
比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),
比值不变。
比的基本性质
商不变规律
分数的基本性质
比
比的意义:
比的基本性质:
比和除法、分数的关系:
求比值:
两个数相除又可以叫作两个数的比。
比的前项除以后项所得的商。
a:b=a÷b= (b≠0)
b
a
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
化简比:
把两个数的比化成最简整数比。
(比的前项与后项互质)
化简比的一般方法:
=(12÷6)∶(18÷6)
12∶18
=2∶3
6
5
4
3
∶
=( ×12)∶( ×12)
6
5
4
3
=10∶9
1.8∶0.09
=(1.8×100)∶(0.09×100)
=180∶9
=20∶1
整数比
比的前项和后项同时除以它们的最大公因数
最简整数比
分数比
比的前项和后项同时乘分母的最小公倍数
小数比
比的前项和后项同时乘十、一百、一千……
依 据
结 果
求比值
化简比
比的意义
(前项÷后项)
一个数
一个比
比的基本性质
(化成最简整数比)
求比值与化简比的区别
比
比的意义:
比的基本性质:
比和除法、分数的关系:
求比值:
两个数相除又可以叫作两个数的比。
比的前项除以后项所得的商。
a:b=a÷b= (b≠0)
b
a
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
化简比:
把两个数的比化成最简单的整数比。
(比的前项与后项互质)
1.(1)六年级一班有男生23 人,女生24 人。男、女生人数的
比是( ), 女生与全班人数的比是( )。
(2)一辆汽车5小时行驶 240千米。这辆汽车行驶的路程与时
间的比是( ),行驶的时间与路程的比是( )。
(3)配制一种盐水,盐和水质量的比是 1︰24, 盐和盐水质
量的比是( ),水和盐水质量的比是( )。
23︰24
24︰47
48︰1
1︰48
1︰25
24︰25
(4)公鸡与母鸡只数的比是3︰7 ,公鸡占总只数的 ,
母鸡占总只数的 。
( )
( )
7
10
( )
( )
3
10
2.一个房间的地面由两种颜色的地砖铺成。
(1)写出两种地砖铺地面积的比,并化简。
地砖块数的比
20∶40=1∶2
(2)如果这个房间的面积是15平方米,两种地砖的铺地面积分别是多少平方米?
15÷(1+2)=5(平方米)
深色:5×1=5(平方米)
浅色:5×2=10(平方米)
深色:15× =5(平方米)
——
1
1+2
浅色:15× =10(平方米)
——
2
1+2
答:深色地砖的铺底面积是5平方米,
浅色地砖的铺底面积是10平方米。
答:深色地砖的铺底面积是5平方米,
浅色地砖的铺底面积是10平方米。
比例
比例的意义:
表示两个比相等的式子叫作比例。
2.
(1)量出每幅图片的长和宽, 并写出长和宽的比。
3.9︰2.7
2.6︰0.8
1.7︰1.7
1.3︰0.9
(2)先估计哪两个比能组成比例,再算一算,看估计得对不对。
2.
(2)先估计哪两个比能组成比例,再算一算,看估计得对不对。
3.9︰2.7=1.3︰0.9
答:第一幅图片和第四幅图片的比能组成比例。
比例
比例的意义:
比例的基本性质:
表示两个比相等的式子叫作比例。
在比例里,两个外项的积等于两个内项的积。
应用比例的基本性质,判断下面每组的两个比能否组成比例。如果能组成比例,把组成的比例写出来。
3.6∶1.8 和 0.5∶0.25
∶ 和18∶24
3.6×0.25=0.9
1.8×0.5=0.9
3.6∶1.8 = 0.5∶0.25
×24=8
×18=
不能组成比例
1
3
——
1
3
——
1
4
——
1
4
——
9
2
——
比例
比例的意义:
解比例:
比例的基本性质:
表示两个比相等的式子叫作比例。
在比例里,两个外项的积等于两个内项的积。
利用比例的基本性质求比例中的未知项。
3. 解比例。
9︰5 = 4.5︰x
︰x = ︰
解:9x = 5×4.5
9x = 22.5
x = 2.5
解:0.4x = 28×0.1
0.4x = 2.8
x = 7
解: x = ×
x =
x =
=
28
x
0.4
0.1
1
10
1
8
1
4
1
8
1
10
1
4
1
8
1
40
1
5
比例
比例的意义:
解比例:
比例的基本性质:
表示两个比相等的式子叫作比例。
在比例里,两个外项的积等于两个内项的积。
利用比例的基本性质求比例中的未知项。
比例尺:
图上距离∶实际距离=比例尺
6.分别量出学校到市民广场、少年宫、体育场和火车站的图上
距离,再根据比例尺算出它们的实际距离。
3cm
4cm
6cm
3cm
解:设学校到体育场的距离是x厘米。
600米=60000厘米
3∶x=1:60000
x=3×60000
x=180000
180000厘米=1800米
答:学校到体育场的实际距离是1800米。
6.分别量出学校到市民广场、少年宫、体育场和火车站的图上
距离,再根据比例尺算出它们的实际距离。
3cm
4cm
6cm
3cm
600×3=1800(米) 600×4=2400(米) 600×6=3600(米)
答:学校到市民广场的实际距离是1800米,到少年宫的实际距离是2400
米,到体育场的实际距离是1800米,到火车站的实际距离是3600米。
比例
比例的意义:
解比例:
比例的基本性质:
表示两个比相等的式子叫作比例。
在比例里,两个外项的积等于两个内项的积。
利用比例的基本性质求比例中的未知项。
比例尺:
图上距离∶实际距离=比例尺
正比例、反比例:
= k (一定)
y
x
x×y=k(一定)
比例
比例的意义:
解比例:
比例的基本性质:
表示两个比相等的式子叫作比例。
在比例里,两个外项的积等于两个内
项的积。
利用比例的基本性质求比例中的未知项。
比例尺:
图上距离∶实际距离=比例尺
正比例和反比例:
=k(一定)
x
y
x×y=k(一定)
a:b=a÷b= (b≠0)
比的前项和后项同时乘或除以相同的数
(0除外),比值不变。
比
比的意义:
比的基本性质:
比和除法、分数的关系:
求比值:
两个数相除又可以叫作两个数的比。
比的前项除以后项所得的商。
b
a
化简比:
把两个数的比化成最简单的整数比。
(比的前项与后项互质)
比 与
比
例的区别
意义不同
比的意义
两个数相除又叫做两个数的比。
比例的意义
表示两个比相等的式子叫做比例。
名称不同
比的各部分名称
比有两个项。比号前面的数叫做比的前项,比号后面的数叫做比的后项。
比例的各部分名称
比例有四个项。组成比例的四个数叫做比例的项,两端的两项叫做比例的的外项,中间的两项叫做比例的内项。
性质不同
比的基本性质
比的前项和后项同时乘或者除以相同的数(0除外),比值不变。
比例的基本性质
在比例里,两个外项的积等于两个内项的积。
应用不同
应用比的意义
求比值。
应用比的性质
化简比。
应用比例的意义
判断两个不能否组成比例。
应用比例的性质
不但可以判断两个比能否组成比例,还可以解比例。
《比和比例的整理与复习》自主练习
一、判断题
1、在比例里,两个外项的积与两个内项积的差是0。( )
2、任意两圆各自的周长和直径的比都可以组成比例。( )
3、一个60°的角,按1︰10的比例尺画在图纸上,图纸上的角
是6°。( )
4、在一个比例里,两个外项互为倒数,其中一个内项是5,另一个
内项是 。( )
5、10∶3=25∶x,求出x的值为20。( )
—
1
5
二、选择题:
1、方程12∶x=5∶3的解为( )。
A、x= B、x=20 C、x=0.8 D、x=
2、一个长方形,长是12厘米,宽是6厘米。
按一定比放大后,长是36厘米,宽是18厘米,它是按( )的比放大的。
按一定比缩小后,长是6厘米,宽是3厘米,它是按( )的比缩小的。
A、2∶1 B、1∶2 C、 3∶1 D、1∶3
3、如果A:5=9:B,那么AB=(? ?)。
A、5 B、9 C、45 D、1
4、在比例尺是1︰20的图纸上,甲、乙两个圆的直径的比是1︰8,那么甲、乙两个
圆的实际直径比是( )。
A、1︰8 B、1︰24 C、3︰8 D、1︰3
—
36
5
—
5
4
