苏教版 六年级数学下册课件图形的运动整理与复习(43页PPT)
文档属性
| 名称 | 苏教版 六年级数学下册课件图形的运动整理与复习(43页PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 00:00:00 | ||
图片预览






文档简介
图形的运动整理与复习
苏教版六年级下册 数学
图形的运动
平移
旋转
放大和缩小
轴对称图形
回顾与整理
生活中的平移与旋转现象
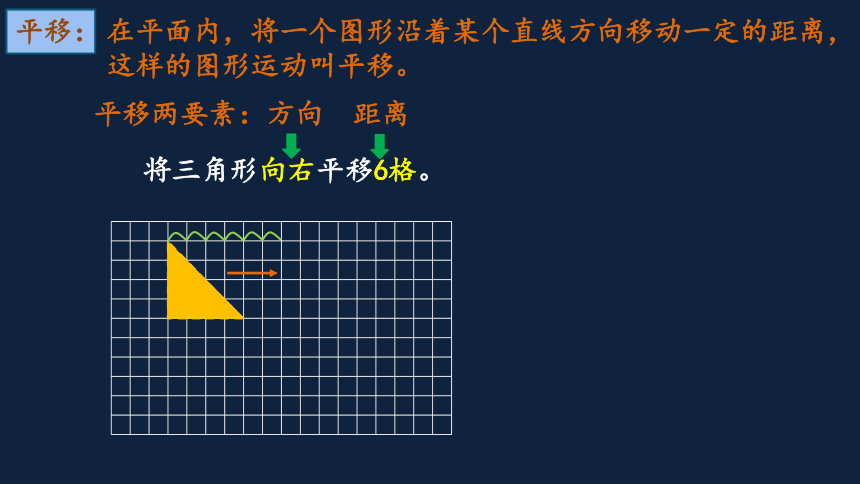
平移:
在平面内,将一个图形沿着某个直线方向移动一定的距离,这样的图形运动叫平移。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
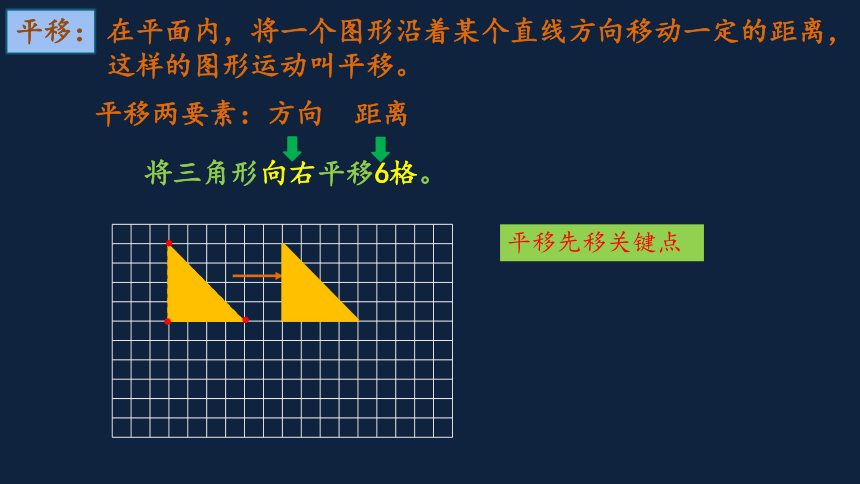
将三角形向右平移6格。
平移两要素:方向 距离
在平面内,将一个图形沿着某个直线方向移动一定的距离,这样的图形运动叫平移。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
将三角形向右平移6格。
平移两要素:方向 距离
平移先移关键点
平移:
在平面内,将一个图形绕着一个点进行圆周运动,这样的图形运动叫旋转。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
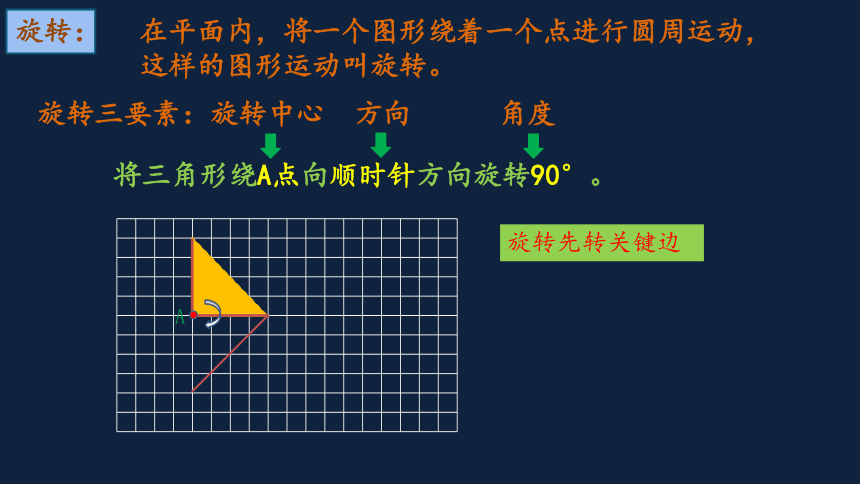
将三角形绕A点向顺时针方向旋转90°。
旋转三要素:旋转中心 方向 角度
A
旋转:
在平面内,将一个图形绕着一个点进行圆周运动,这样的图形运动叫旋转。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
将三角形绕A点向顺时针方向旋转90°。
旋转三要素:旋转中心 方向 角度
A
旋转先转关键边
旋转:
想一想:图形经过平移或旋转后,什么变了?什么不变?
平移和旋转只改变图形的位置,不改变图形的大小和形状。
图形的运动
平移
旋转
放大和缩小
轴对称图形
方向,距离
旋转中心,方向,角度
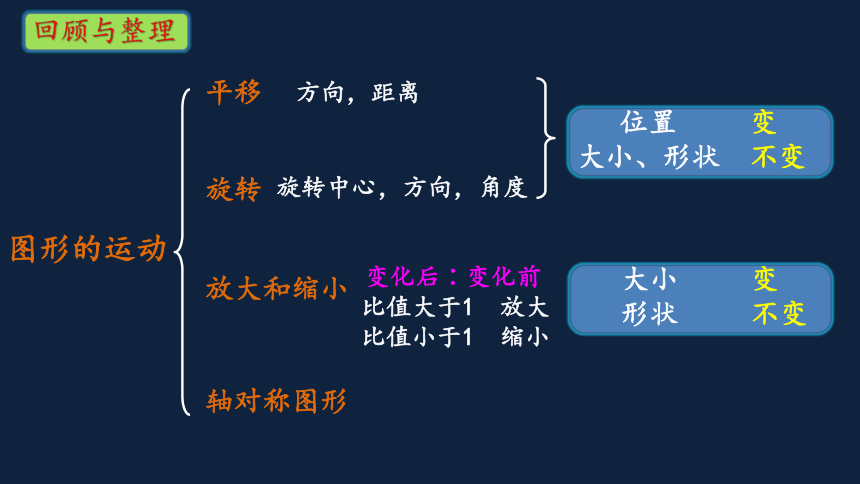
回顾与整理
位置 变 大小、形状 不变
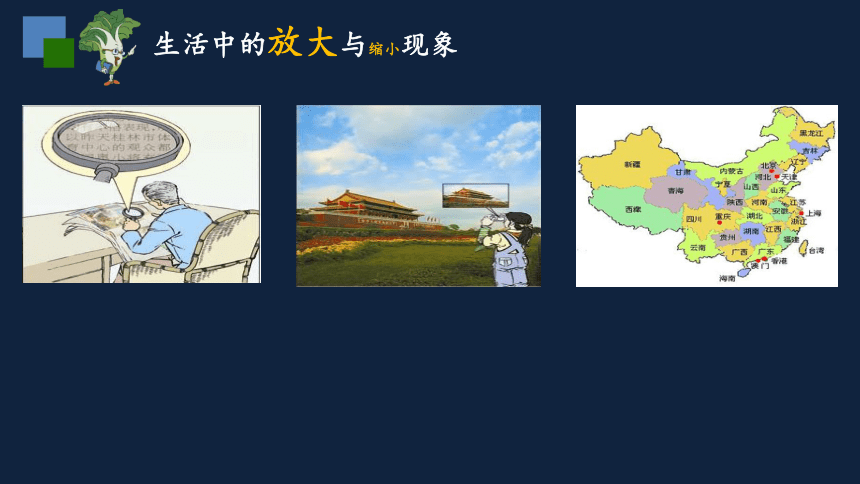
生活中的放大与缩小现象
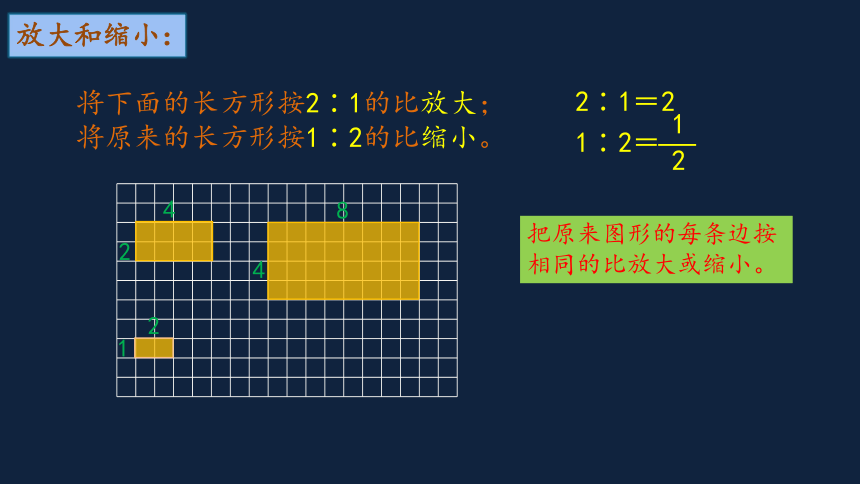
放大和缩小:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
将下面的长方形按2∶1的比放大;
将原来的长方形按1∶2的比缩小。
把原来图形的每条边按相同的比放大或缩小。
4
2
8
4
2
1
2∶1=2
1
2
1∶2=
图形的运动
平移
旋转
放大和缩小
轴对称图形
方向,距离
旋转中心,方向,角度
比值大于1 放大
比值小于1 缩小
回顾与整理
变化后∶变化前
位置 变 大小、形状 不变
大小 变
形状 不变
生活中的轴对称现象
轴对称图形:
对折后折痕两边完全重合的图形,叫轴对称图形。
折痕所在的直线叫对称轴。
轴对称图形:
我们认识的图形中,哪些是轴对称图形?各有几条对称轴?
轴对称图形:
我们认识的图形中,哪些是轴对称图形?各有几条对称轴?
正多边形都是轴对称图形。
正三角形
正四边形
正五边形
正六边形
3条
4条
5条
6条
轴对称图形:
正八边形
正十边形
正十二边形
正十七边形
……
圆
8条
10条
12条
17条
无数条
正三角形
正四边形
正五边形
正六边形
3条
4条
5条
6条
正多边形有几条边,就有几条对称轴。
轴对称图形:
1. 下面哪些图形是轴对称图形? 画出轴对称图形的对称轴。
图形的运动
平移
旋转
放大和缩小
轴对称图形
方向,距离
旋转中心,方向,角度
位置 变 大小、形状 不变
大小 变
形状 不变
回顾与整理
对折后 完全重合
比值大于1 放大
比值小于1 缩小
变化后∶变化前
(对称美)
2. (1)画出图A的另一半,使它成为一个轴对称图形。
2. (2)把图B向右平移5格,再向上平移3格。
2. (3)把图C绕点O逆时针旋转90°。
C
C
2. (4)把图D按 3︰1的比放大。
3
2
4
9
6
12
C
3. 按 1︰2 的比画出三角形缩小后的图形。
新图形与原来图形面积的比是几比几?
8
4
4
2
3. 按 1︰2 的比画出三角形缩小后的图形。
2×4÷2=4
4×8÷2=16
4︰16=1︰4
答:新图形与原来图形面积的比是1︰4。
新图形与原来图形面积的比是几比几?
8
4
4
2
新图形面积:
原图形面积:
新图形和原图形面积比:
新图形面积:(9+12)×6÷2=63
原图形面积: (3+4)×2÷2=7
面积比: 63∶7=9∶1
按 3︰1 的比画出梯形放大后的图形。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}放大或缩小
对应边的比
面积的比
梯形按3∶1放大
3∶1
9∶1
三角形按1∶2缩小
1∶2
1∶4
比较
4. 把左边的圆平移,使平移后的圆与右边的线段组成轴对称图形。
(1)圆应向什么方向平移几格?
(2)你能画出组成的轴对称图形的
对称轴吗?
(3)对称轴通过圆心吗?它与已知
线段有什么关系?
答:圆应向右平移5格。
O
剪两个同样大的正方形,把其中一个正方形的顶点固定在另一个正方形的中心点上。旋转其中一个正方形,重叠部分的面积有没有变化?
割补法:
发现:
这样摆放的两个同样大的正方形,无论把其中一个正方形怎样旋转,重叠部分的面积都等于正方形面积的 。
1
4
思维大闯关
剪两个同样大的正方形,把其中一个正方形的顶点固定在另一个正方形的中心点上。旋转其中一个正方形,重叠部分的面积有没有变化?
发现:
这样摆放的两个同样大的正方形,无论把其中一个正方形怎样旋转,重叠部分的面积都等于正方形面积的 。
1
4
思维大闯关
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
求下面图形的周长
周长:
(6+5)×2
=11×2
=22
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
用两个完全相同的三角形拼成一个平行四边形。
点动成线
线动成面
面动成体
设计1:在下面的图形中再给2个格子图上红色,使涂色部分成为一个轴对称图形。有几种不同的涂法?
小小设计师
小小设计师
设计2:运用平移、旋转设计美丽的图案。
小小设计师
设计2:运用平移、旋转设计美丽的图案。
5. 从左边四种瓷砖中选择两种,可以拼成不同的图案(如下图)。
(1)这两个图案各选择了哪几种瓷砖?
①
②
③
④
(2)任意选择两种瓷砖,设计几种不同的图案,与同学交流。
小小设计师
设计3:综合运用大比拼。
图形的运动
平移
旋转
放大和缩小
轴对称图形
方向,距离
旋转中心,方向,角度
位置 变 大小、形状不变
按2:1是放大
按1:2是缩小
大小 变
形状 不变
对折后 完全重合(对称美)
总结与反思
知识
方法
数学眼光
《图形的运动》学生自主练习
一、判断:
1、长方形、等腰梯形、平行四边形、圆都是轴对称图形。 ( )
2、一个圆形,按4︰1的比放大后,周长扩大到原来的4倍,
面积扩大到原来的16倍。 ( )
3、沿着直线导轨推拉一扇玻璃窗,玻璃窗的运动是平移。 ( )
4、把长方形按1︰3变换后,长方形的边线被扩大了3倍。 ( )
5、把图形 绕O点逆时针旋转90°后,得到的图形是 。( )
O
O
二、选择:
1、下面的图形中,( )的对称轴最多。
A.正方形 B.等边三角形 C.等腰梯形 D.长方形
2、把右图绕点O顺时针方向旋转90°,得到的图案是( );
逆时针旋转90°,得到的图案是( )。
O
O
O
O
O
A.
B.
C.
D.
3、美术老师想将一幅图放大后放在橱窗里展览,他调到200%来复印,
这幅图是按照( )的比复印出来的。
A. 1︰2 B. 2︰1 C. 1︰200 D. 200︰1
4、给右图中的1个白色小方格涂上颜色,使涂色部分
成为一个轴对称图形,有( )种涂法。
A. 3 B. 4 C. 5 D. 6
5、下面的图案中,只能通过基本图案平移得到的是( )。
A.
B.
C.
D.
苏教版六年级下册 数学
图形的运动
平移
旋转
放大和缩小
轴对称图形
回顾与整理
生活中的平移与旋转现象
平移:
在平面内,将一个图形沿着某个直线方向移动一定的距离,这样的图形运动叫平移。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
将三角形向右平移6格。
平移两要素:方向 距离
在平面内,将一个图形沿着某个直线方向移动一定的距离,这样的图形运动叫平移。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
将三角形向右平移6格。
平移两要素:方向 距离
平移先移关键点
平移:
在平面内,将一个图形绕着一个点进行圆周运动,这样的图形运动叫旋转。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
将三角形绕A点向顺时针方向旋转90°。
旋转三要素:旋转中心 方向 角度
A
旋转:
在平面内,将一个图形绕着一个点进行圆周运动,这样的图形运动叫旋转。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
将三角形绕A点向顺时针方向旋转90°。
旋转三要素:旋转中心 方向 角度
A
旋转先转关键边
旋转:
想一想:图形经过平移或旋转后,什么变了?什么不变?
平移和旋转只改变图形的位置,不改变图形的大小和形状。
图形的运动
平移
旋转
放大和缩小
轴对称图形
方向,距离
旋转中心,方向,角度
回顾与整理
位置 变 大小、形状 不变
生活中的放大与缩小现象
放大和缩小:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
将下面的长方形按2∶1的比放大;
将原来的长方形按1∶2的比缩小。
把原来图形的每条边按相同的比放大或缩小。
4
2
8
4
2
1
2∶1=2
1
2
1∶2=
图形的运动
平移
旋转
放大和缩小
轴对称图形
方向,距离
旋转中心,方向,角度
比值大于1 放大
比值小于1 缩小
回顾与整理
变化后∶变化前
位置 变 大小、形状 不变
大小 变
形状 不变
生活中的轴对称现象
轴对称图形:
对折后折痕两边完全重合的图形,叫轴对称图形。
折痕所在的直线叫对称轴。
轴对称图形:
我们认识的图形中,哪些是轴对称图形?各有几条对称轴?
轴对称图形:
我们认识的图形中,哪些是轴对称图形?各有几条对称轴?
正多边形都是轴对称图形。
正三角形
正四边形
正五边形
正六边形
3条
4条
5条
6条
轴对称图形:
正八边形
正十边形
正十二边形
正十七边形
……
圆
8条
10条
12条
17条
无数条
正三角形
正四边形
正五边形
正六边形
3条
4条
5条
6条
正多边形有几条边,就有几条对称轴。
轴对称图形:
1. 下面哪些图形是轴对称图形? 画出轴对称图形的对称轴。
图形的运动
平移
旋转
放大和缩小
轴对称图形
方向,距离
旋转中心,方向,角度
位置 变 大小、形状 不变
大小 变
形状 不变
回顾与整理
对折后 完全重合
比值大于1 放大
比值小于1 缩小
变化后∶变化前
(对称美)
2. (1)画出图A的另一半,使它成为一个轴对称图形。
2. (2)把图B向右平移5格,再向上平移3格。
2. (3)把图C绕点O逆时针旋转90°。
C
C
2. (4)把图D按 3︰1的比放大。
3
2
4
9
6
12
C
3. 按 1︰2 的比画出三角形缩小后的图形。
新图形与原来图形面积的比是几比几?
8
4
4
2
3. 按 1︰2 的比画出三角形缩小后的图形。
2×4÷2=4
4×8÷2=16
4︰16=1︰4
答:新图形与原来图形面积的比是1︰4。
新图形与原来图形面积的比是几比几?
8
4
4
2
新图形面积:
原图形面积:
新图形和原图形面积比:
新图形面积:(9+12)×6÷2=63
原图形面积: (3+4)×2÷2=7
面积比: 63∶7=9∶1
按 3︰1 的比画出梯形放大后的图形。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}放大或缩小
对应边的比
面积的比
梯形按3∶1放大
3∶1
9∶1
三角形按1∶2缩小
1∶2
1∶4
比较
4. 把左边的圆平移,使平移后的圆与右边的线段组成轴对称图形。
(1)圆应向什么方向平移几格?
(2)你能画出组成的轴对称图形的
对称轴吗?
(3)对称轴通过圆心吗?它与已知
线段有什么关系?
答:圆应向右平移5格。
O
剪两个同样大的正方形,把其中一个正方形的顶点固定在另一个正方形的中心点上。旋转其中一个正方形,重叠部分的面积有没有变化?
割补法:
发现:
这样摆放的两个同样大的正方形,无论把其中一个正方形怎样旋转,重叠部分的面积都等于正方形面积的 。
1
4
思维大闯关
剪两个同样大的正方形,把其中一个正方形的顶点固定在另一个正方形的中心点上。旋转其中一个正方形,重叠部分的面积有没有变化?
发现:
这样摆放的两个同样大的正方形,无论把其中一个正方形怎样旋转,重叠部分的面积都等于正方形面积的 。
1
4
思维大闯关
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
求下面图形的周长
周长:
(6+5)×2
=11×2
=22
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
用两个完全相同的三角形拼成一个平行四边形。
点动成线
线动成面
面动成体
设计1:在下面的图形中再给2个格子图上红色,使涂色部分成为一个轴对称图形。有几种不同的涂法?
小小设计师
小小设计师
设计2:运用平移、旋转设计美丽的图案。
小小设计师
设计2:运用平移、旋转设计美丽的图案。
5. 从左边四种瓷砖中选择两种,可以拼成不同的图案(如下图)。
(1)这两个图案各选择了哪几种瓷砖?
①
②
③
④
(2)任意选择两种瓷砖,设计几种不同的图案,与同学交流。
小小设计师
设计3:综合运用大比拼。
图形的运动
平移
旋转
放大和缩小
轴对称图形
方向,距离
旋转中心,方向,角度
位置 变 大小、形状不变
按2:1是放大
按1:2是缩小
大小 变
形状 不变
对折后 完全重合(对称美)
总结与反思
知识
方法
数学眼光
《图形的运动》学生自主练习
一、判断:
1、长方形、等腰梯形、平行四边形、圆都是轴对称图形。 ( )
2、一个圆形,按4︰1的比放大后,周长扩大到原来的4倍,
面积扩大到原来的16倍。 ( )
3、沿着直线导轨推拉一扇玻璃窗,玻璃窗的运动是平移。 ( )
4、把长方形按1︰3变换后,长方形的边线被扩大了3倍。 ( )
5、把图形 绕O点逆时针旋转90°后,得到的图形是 。( )
O
O
二、选择:
1、下面的图形中,( )的对称轴最多。
A.正方形 B.等边三角形 C.等腰梯形 D.长方形
2、把右图绕点O顺时针方向旋转90°,得到的图案是( );
逆时针旋转90°,得到的图案是( )。
O
O
O
O
O
A.
B.
C.
D.
3、美术老师想将一幅图放大后放在橱窗里展览,他调到200%来复印,
这幅图是按照( )的比复印出来的。
A. 1︰2 B. 2︰1 C. 1︰200 D. 200︰1
4、给右图中的1个白色小方格涂上颜色,使涂色部分
成为一个轴对称图形,有( )种涂法。
A. 3 B. 4 C. 5 D. 6
5、下面的图案中,只能通过基本图案平移得到的是( )。
A.
B.
C.
D.
