六年级下册数学课件 正比例的图像 苏教版(24张ppt)
文档属性
| 名称 | 六年级下册数学课件 正比例的图像 苏教版(24张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 8.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 13:49:01 | ||
图片预览

文档简介
正比例的图像
苏教版六年级下册 数学
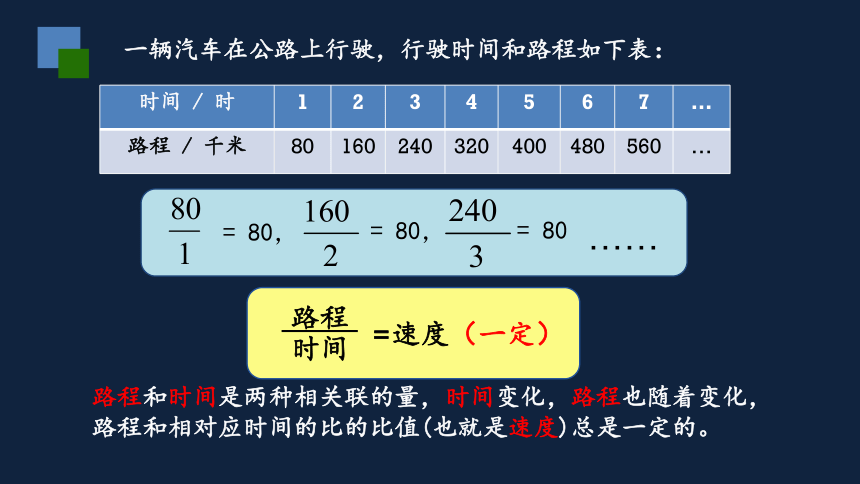
= 80,
= 80,
= 80
……
一辆汽车在公路上行驶,行驶时间和路程如下表:
时间 / 时
1
2
3
4
5
6
7
…
路程 / 千米
80
160
240
320
400
480
560
…
路程
时间
速度(一定)
=
路程和时间是两种相关联的量,时间变化,路程也随着变化,路程和相对应时间的比的比值(也就是速度)总是一定的。
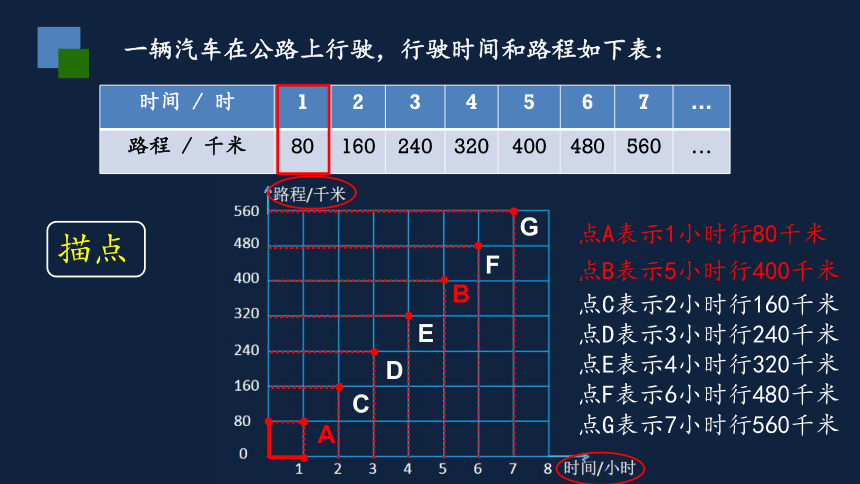
一辆汽车在公路上行驶,行驶时间和路程如下表:
时间 / 时
1
2
3
4
5
6
7
…
路程 / 千米
80
160
240
320
400
480
560
…
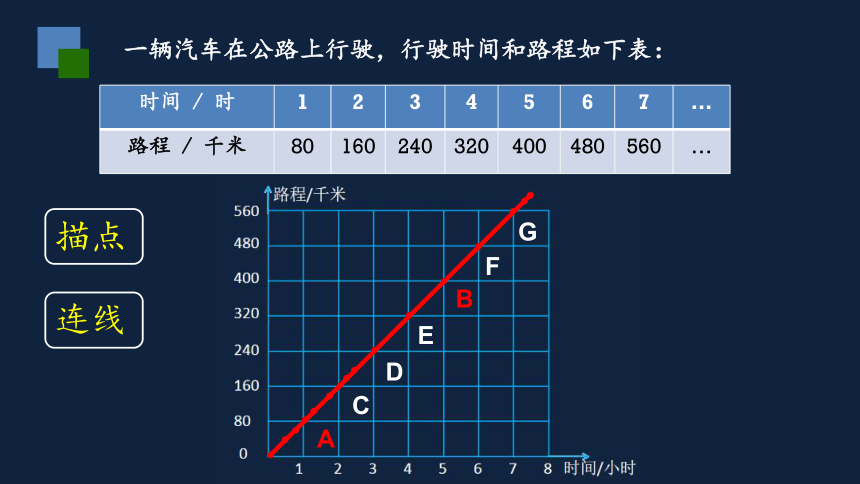
A
点A表示1小时行80千米
描点
点B表示5小时行400千米
B
点C表示2小时行160千米
点D表示3小时行240千米
点E表示4小时行320千米
点F表示6小时行480千米
点G表示7小时行560千米
C
D
E
F
G
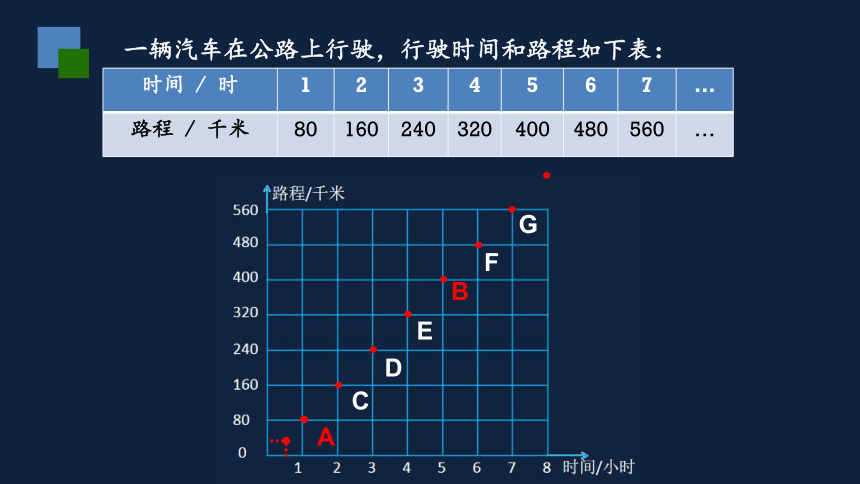
一辆汽车在公路上行驶,行驶时间和路程如下表:
时间 / 时
1
2
3
4
5
6
7
…
路程 / 千米
80
160
240
320
400
480
560
…
A
B
C
D
E
F
G
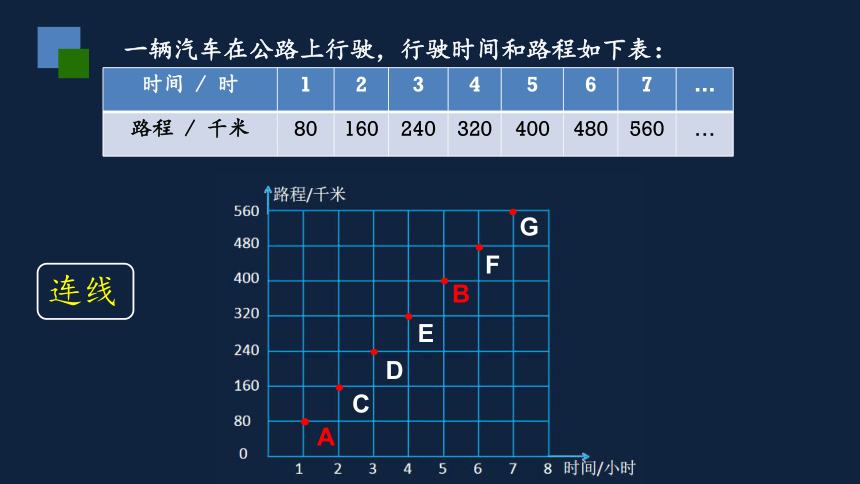
一辆汽车在公路上行驶,行驶时间和路程如下表:
时间 / 时
1
2
3
4
5
6
7
…
路程 / 千米
80
160
240
320
400
480
560
…
A
B
C
D
E
F
G
连线
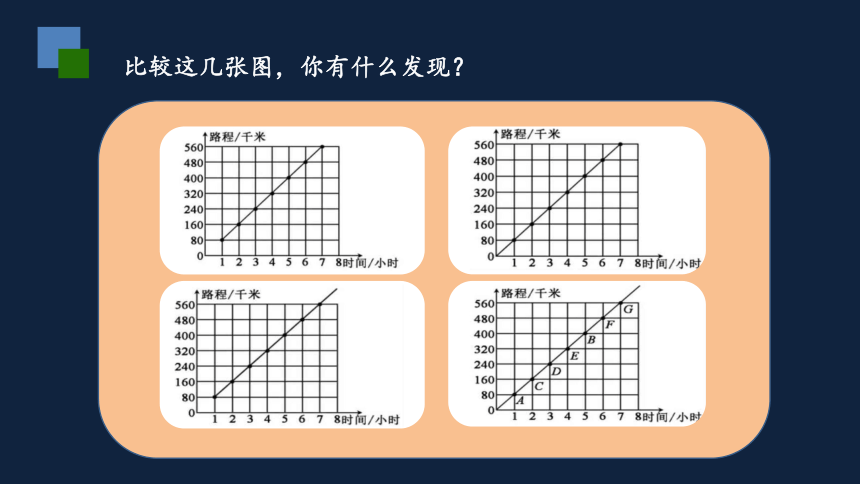
比较这几张图,你有什么发现?
一辆汽车在公路上行驶,行驶时间和路程如下表:
时间 / 时
1
2
3
4
5
6
7
…
路程 / 千米
80
160
240
320
400
480
560
…
A
B
C
D
E
F
G
连线
描点
A
B
C
D
E
F
G
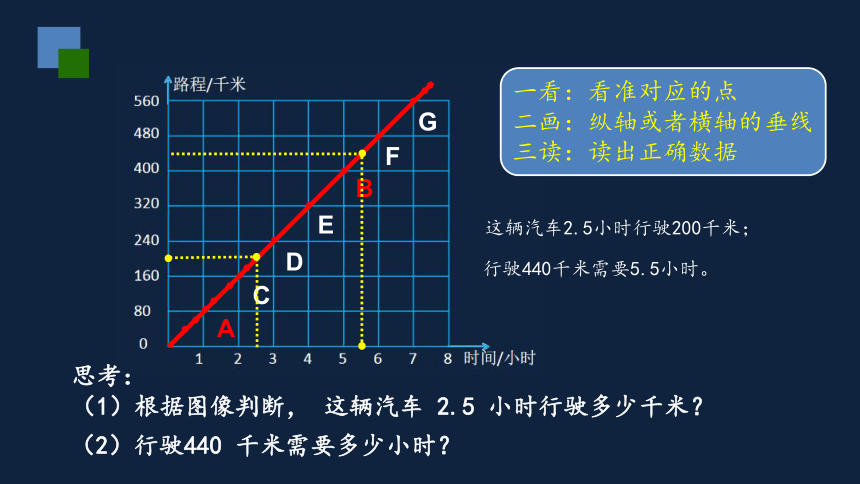
思考:
(1)根据图像判断, 这辆汽车 2.5 小时行驶多少千米?
(2)行驶440 千米需要多少小时?
一看:看准对应的点
二画:纵轴或者横轴的垂线
三读:读出正确数据
这辆汽车2.5小时行驶200千米;
行驶440千米需要5.5小时。
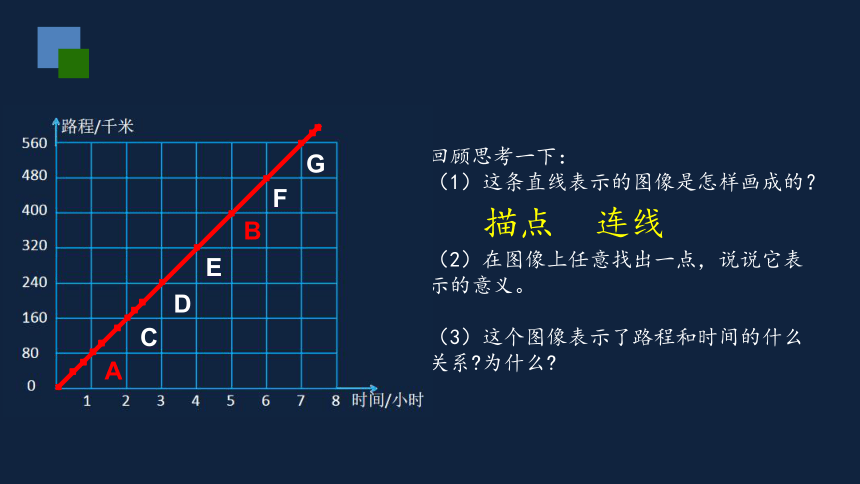
回顾思考一下:
(1)这条直线表示的图像是怎样画成的?
(2)在图像上任意找出一点,说说它表示的意义。
(3)这个图像表示了路程和时间的什么关系?为什么?
连线
描点
A
B
C
D
E
F
G
小玲用计算机打字的数量和所用的时间如下表:
(1)小玲打字的数量和所用的时间成正比例吗?为什么?
……
,
,
小玲打字的数量和所用的时间成正比例。
∵
∴
(2)在下图中描出打字数量和时间所对应的点,再按顺序连接起来。
小玲用计算机打字的数量和所用的时间如下表:
(3)根据图像判断,小玲5分钟可以打多少个字?
打750个字需要多少分钟?
答:小玲5分钟可
以打250个字,打
750个字需要15分
钟。
小玲用计算机打字的数量和所用的时间如下表:
A
B
C
D
E
F
G
比较这两张正比例图像,你发现有什么相同的地方?
练习十
∵
∴他们骑车行的路程和时间成正比例。
因为图像呈一条直线,所以他们骑车行的路程和时间成正比例。
A 30分钟行8千米
B 60分钟行16千米
C 90分钟行24千米
A
B
C
练习十
练习十
练习十
练习十
(2)物体的质量与弹簧伸长的长度成正比例吗?为什么?
因为图像呈一条直线,所以物体的质量与弹簧伸长的长度成正比例。
练习十
小挑战
A
B
C
三辆车,分别在限速大桥、公路、高速公路上行驶,你知道究竟是哪辆车行驶在高速公路上吗?
回顾总结
说说你有什么收获?
正比例的图像
特点
是一条直线
反映两种量的正比例关系
根据图像判断估计
研究方法
观察
描点
连线
法国数学家
——笛卡尔
数学史上最伟大的转折点就是笛卡尔的变数。
他用运动的观点,把变数引入数学,建立坐标系,把点与数相对应,用方程来解决图形问题。
数学在思想方法上发生了根本的转折,由常量数学进入了变量数学时期。
小知识
《正比例的图像》(自主练习)
一、判断
(1)一个正数和它的倒数成正比例。 ( )
(2)正方体的棱长和与棱长成正比例。 ( )
(3)三角形的面积一定,底和高成正比例。 ( )
(4)正方体的表面积与底面积成正比例。 ( )
(5)小圆周长和大圆周长之比为1 :2,那么它们的面积比为1 :4。 ( )
二、选择
1、钟表上的一种零件长为3mm,画在图纸上长为12cm,这幅图纸的比例尺是(????)。?
A?40:1?? B?1:40? ?C??4:1
2、一个圆柱和一个圆锥的体积相等,圆柱和圆锥底面积的比是3:1,高的比是(? ??)。
? A 1:3???????B 3:1???????C 1:9?
3、大豆的出油率一定,大豆的出油量(千克数)与大豆的重量(千克数)(??? ?)。?
A 成正比例 B 不成比例
4、圆的面积和( )成正比例。
A 半径 B 直径 C 半径的平方
5、如果5x=y,那么x与y成(?????)比例
A 成正比例 B 不成比例
苏教版六年级下册 数学
= 80,
= 80,
= 80
……
一辆汽车在公路上行驶,行驶时间和路程如下表:
时间 / 时
1
2
3
4
5
6
7
…
路程 / 千米
80
160
240
320
400
480
560
…
路程
时间
速度(一定)
=
路程和时间是两种相关联的量,时间变化,路程也随着变化,路程和相对应时间的比的比值(也就是速度)总是一定的。
一辆汽车在公路上行驶,行驶时间和路程如下表:
时间 / 时
1
2
3
4
5
6
7
…
路程 / 千米
80
160
240
320
400
480
560
…
A
点A表示1小时行80千米
描点
点B表示5小时行400千米
B
点C表示2小时行160千米
点D表示3小时行240千米
点E表示4小时行320千米
点F表示6小时行480千米
点G表示7小时行560千米
C
D
E
F
G
一辆汽车在公路上行驶,行驶时间和路程如下表:
时间 / 时
1
2
3
4
5
6
7
…
路程 / 千米
80
160
240
320
400
480
560
…
A
B
C
D
E
F
G
一辆汽车在公路上行驶,行驶时间和路程如下表:
时间 / 时
1
2
3
4
5
6
7
…
路程 / 千米
80
160
240
320
400
480
560
…
A
B
C
D
E
F
G
连线
比较这几张图,你有什么发现?
一辆汽车在公路上行驶,行驶时间和路程如下表:
时间 / 时
1
2
3
4
5
6
7
…
路程 / 千米
80
160
240
320
400
480
560
…
A
B
C
D
E
F
G
连线
描点
A
B
C
D
E
F
G
思考:
(1)根据图像判断, 这辆汽车 2.5 小时行驶多少千米?
(2)行驶440 千米需要多少小时?
一看:看准对应的点
二画:纵轴或者横轴的垂线
三读:读出正确数据
这辆汽车2.5小时行驶200千米;
行驶440千米需要5.5小时。
回顾思考一下:
(1)这条直线表示的图像是怎样画成的?
(2)在图像上任意找出一点,说说它表示的意义。
(3)这个图像表示了路程和时间的什么关系?为什么?
连线
描点
A
B
C
D
E
F
G
小玲用计算机打字的数量和所用的时间如下表:
(1)小玲打字的数量和所用的时间成正比例吗?为什么?
……
,
,
小玲打字的数量和所用的时间成正比例。
∵
∴
(2)在下图中描出打字数量和时间所对应的点,再按顺序连接起来。
小玲用计算机打字的数量和所用的时间如下表:
(3)根据图像判断,小玲5分钟可以打多少个字?
打750个字需要多少分钟?
答:小玲5分钟可
以打250个字,打
750个字需要15分
钟。
小玲用计算机打字的数量和所用的时间如下表:
A
B
C
D
E
F
G
比较这两张正比例图像,你发现有什么相同的地方?
练习十
∵
∴他们骑车行的路程和时间成正比例。
因为图像呈一条直线,所以他们骑车行的路程和时间成正比例。
A 30分钟行8千米
B 60分钟行16千米
C 90分钟行24千米
A
B
C
练习十
练习十
练习十
练习十
(2)物体的质量与弹簧伸长的长度成正比例吗?为什么?
因为图像呈一条直线,所以物体的质量与弹簧伸长的长度成正比例。
练习十
小挑战
A
B
C
三辆车,分别在限速大桥、公路、高速公路上行驶,你知道究竟是哪辆车行驶在高速公路上吗?
回顾总结
说说你有什么收获?
正比例的图像
特点
是一条直线
反映两种量的正比例关系
根据图像判断估计
研究方法
观察
描点
连线
法国数学家
——笛卡尔
数学史上最伟大的转折点就是笛卡尔的变数。
他用运动的观点,把变数引入数学,建立坐标系,把点与数相对应,用方程来解决图形问题。
数学在思想方法上发生了根本的转折,由常量数学进入了变量数学时期。
小知识
《正比例的图像》(自主练习)
一、判断
(1)一个正数和它的倒数成正比例。 ( )
(2)正方体的棱长和与棱长成正比例。 ( )
(3)三角形的面积一定,底和高成正比例。 ( )
(4)正方体的表面积与底面积成正比例。 ( )
(5)小圆周长和大圆周长之比为1 :2,那么它们的面积比为1 :4。 ( )
二、选择
1、钟表上的一种零件长为3mm,画在图纸上长为12cm,这幅图纸的比例尺是(????)。?
A?40:1?? B?1:40? ?C??4:1
2、一个圆柱和一个圆锥的体积相等,圆柱和圆锥底面积的比是3:1,高的比是(? ??)。
? A 1:3???????B 3:1???????C 1:9?
3、大豆的出油率一定,大豆的出油量(千克数)与大豆的重量(千克数)(??? ?)。?
A 成正比例 B 不成比例
4、圆的面积和( )成正比例。
A 半径 B 直径 C 半径的平方
5、如果5x=y,那么x与y成(?????)比例
A 成正比例 B 不成比例
