18.1.1 平行四边形的性质(1) 课件(共18张PPT)
文档属性
| 名称 | 18.1.1 平行四边形的性质(1) 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
人教版
八年级下
18.1.1平行四边形的性质(1)
1.理解平行四边形的概念和性质
2.经历平行四边形性质的探究、归纳过程,体会通过操作、观察、猜想、论证获得数学知识的方法;同时,发展分析、归纳、概括能力,提升数学思维品质
3.能运用平行四边形性质解决简单实际问题,体会用代数方法解几何问题的数学思想方法。
教学目标
1、
的四边形叫平行四边形.
两组对边分别平行
2、平行四边形可用符号“
”表示;
平行四边形ABCD
记作:
;
ABCD
注意:图形中字母的标识顺序应为顺时针方向或逆时针方向。
知识回顾
3、如图,在
ABCD中,
对边有
组,分别是
;
对角有
组,分是
;
对角线有
条,它们是
.
两
AB与CD,AD与BC
两
∠BAD与∠BCD,∠ABC与∠ADC
两
AC、BD
A
D
C
B
知识回顾
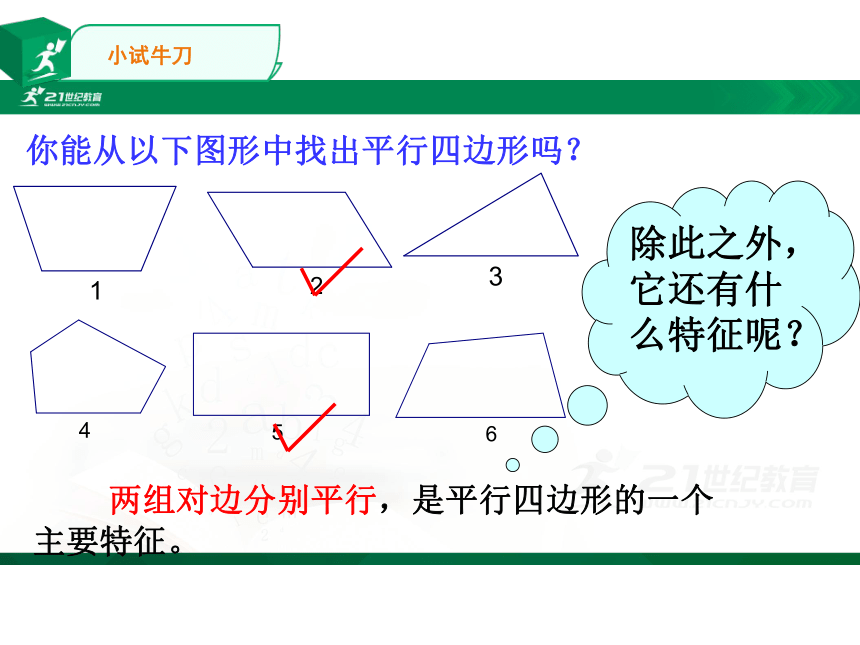
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征。
除此之外,它还有什么特征呢?
小试牛刀
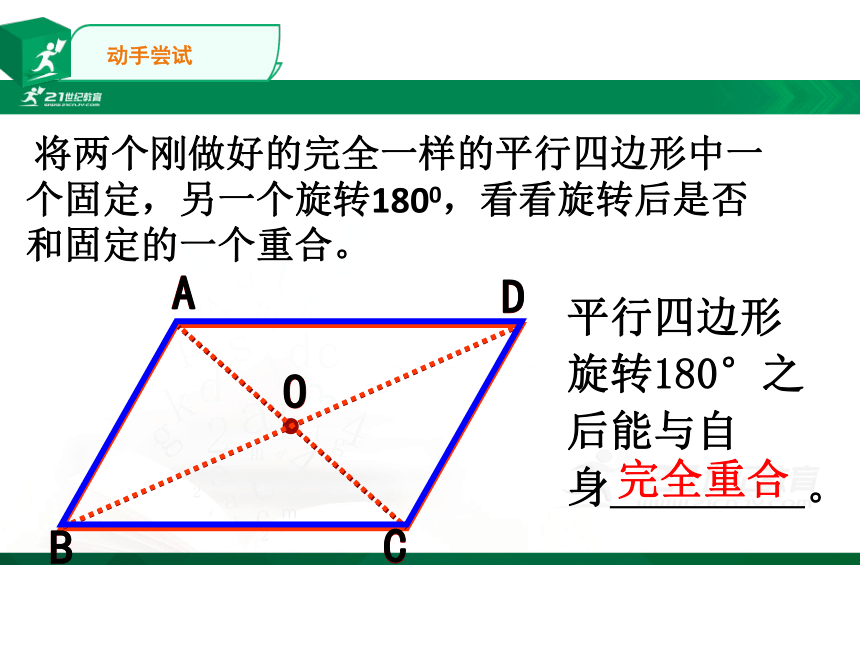
将两个刚做好的完全一样的平行四边形中一个固定,另一个旋转1800,看看旋转后是否和固定的一个重合。
平行四边形旋转180°之后能与自身
。
完全重合
●
A
D
O
C
B
D
B
O
C
A
动手尝试
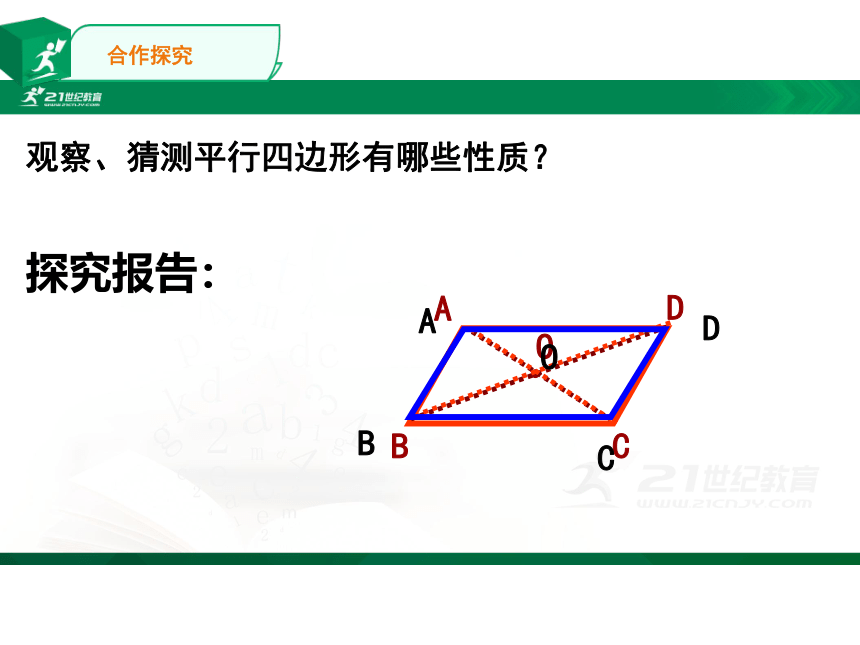
观察、猜测平行四边形有哪些性质?
探究报告:
●
A
D
O
C
B
D
B
O
C
A
合作探究
研究对象
研究结果
几何表示
对边
对角
邻角
平行且相等
AB
CD
AD
BC
相等
互补
∠A+∠B=180°∠C+∠D=180°
∠A+∠D=180°∠C+∠B=180°
=
∥
平行且相等
∥
=
∠A=∠C
∠
B=∠D
合作探究
已知:
ABCD
求证:AB=CD,BC=DA;∠B=∠D,∠BAD=∠DCB.
A
B
C
D
1
2
3
4
验证猜想
证明:连接AC
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
方法总结:作对角线是解决四边形问题常用的辅助线,通过作对角线,可以把未知四边形问题转化为已知的关于三角形的问题.
∴∠1=∠2,∠3=∠4
在△ABC和△CDA中
∠1=∠2
AC=CA
∠3=∠4
∴
△ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
即∠BAD=∠DCB
平行四边形的对边平行
平行四边形的对边相等
平行四边形的对角相等
平行四边形的邻角互补
平行四边形的性质
归纳总结
符号语言:
∵
四边形ABCD是平行四边形
AB
=
CD,AD
=
BC.
(平行四边形的对边相等)
∠A
=∠C,
∠B
=∠D
(平行四边形的对角相等)
平行四边形的性质
∴AB∥CD,AD∥BC
(平行四边形的对边平行)
AB
CD,
AD
BC;
=
∥
=
∥
归纳总结
例
1
如图,在
ABCD中,
DE⊥AB
,
BF⊥CD,垂足分
别为E
,
F.求证
AE
=
CF.
B
A
C
D
E
F
证明:∵四边形ABCD
是平行四边形
∴∠A=∠C
(平行四边形对角相等)
AD=BC
(平行四边形对边相等)
∵DE⊥AB,BF⊥CD
∴∠AED=∠CFB=90°
在△AED和△CFB中
∠A=∠C
∠AED=∠CFB
AD=BC
∴△AED≌△CFB
(AAS)
∴AE=CF(全等三角形对应边相等)
例题讲解
1.如图:在
ABCD中,根据已知你能求出其它的边和角吗?说说你的理由
32cm
30cm
32cm
30cm
A
B
C
D
56°
56°
124°
124°
小试牛刀
1、已知
ABCD中,AB=8,BC=4,
其余各边长为多少?其周长等于多少?
A
B
C
D
2、已知
ABCD的周长是20,AB=6,
则BC=_
CD=__.
3、已知:
ABCD中,∠D=100°,你能求出
其他各角的度数吗?说说你的理由.
4、
中,∠A比∠B大30°,则∠A=_,∠D=__.
ABCD
小试牛刀
平行四边形的性质
边
平行四边形的对边平行且相等;
角
B
D
C
A
平行四边形的对角相等;
(邻角互补)
感悟与收获
https://www.21cnjy.com/help/help_extract.php
人教版
八年级下
18.1.1平行四边形的性质(1)
1.理解平行四边形的概念和性质
2.经历平行四边形性质的探究、归纳过程,体会通过操作、观察、猜想、论证获得数学知识的方法;同时,发展分析、归纳、概括能力,提升数学思维品质
3.能运用平行四边形性质解决简单实际问题,体会用代数方法解几何问题的数学思想方法。
教学目标
1、
的四边形叫平行四边形.
两组对边分别平行
2、平行四边形可用符号“
”表示;
平行四边形ABCD
记作:
;
ABCD
注意:图形中字母的标识顺序应为顺时针方向或逆时针方向。
知识回顾
3、如图,在
ABCD中,
对边有
组,分别是
;
对角有
组,分是
;
对角线有
条,它们是
.
两
AB与CD,AD与BC
两
∠BAD与∠BCD,∠ABC与∠ADC
两
AC、BD
A
D
C
B
知识回顾
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征。
除此之外,它还有什么特征呢?
小试牛刀
将两个刚做好的完全一样的平行四边形中一个固定,另一个旋转1800,看看旋转后是否和固定的一个重合。
平行四边形旋转180°之后能与自身
。
完全重合
●
A
D
O
C
B
D
B
O
C
A
动手尝试
观察、猜测平行四边形有哪些性质?
探究报告:
●
A
D
O
C
B
D
B
O
C
A
合作探究
研究对象
研究结果
几何表示
对边
对角
邻角
平行且相等
AB
CD
AD
BC
相等
互补
∠A+∠B=180°∠C+∠D=180°
∠A+∠D=180°∠C+∠B=180°
=
∥
平行且相等
∥
=
∠A=∠C
∠
B=∠D
合作探究
已知:
ABCD
求证:AB=CD,BC=DA;∠B=∠D,∠BAD=∠DCB.
A
B
C
D
1
2
3
4
验证猜想
证明:连接AC
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
方法总结:作对角线是解决四边形问题常用的辅助线,通过作对角线,可以把未知四边形问题转化为已知的关于三角形的问题.
∴∠1=∠2,∠3=∠4
在△ABC和△CDA中
∠1=∠2
AC=CA
∠3=∠4
∴
△ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
即∠BAD=∠DCB
平行四边形的对边平行
平行四边形的对边相等
平行四边形的对角相等
平行四边形的邻角互补
平行四边形的性质
归纳总结
符号语言:
∵
四边形ABCD是平行四边形
AB
=
CD,AD
=
BC.
(平行四边形的对边相等)
∠A
=∠C,
∠B
=∠D
(平行四边形的对角相等)
平行四边形的性质
∴AB∥CD,AD∥BC
(平行四边形的对边平行)
AB
CD,
AD
BC;
=
∥
=
∥
归纳总结
例
1
如图,在
ABCD中,
DE⊥AB
,
BF⊥CD,垂足分
别为E
,
F.求证
AE
=
CF.
B
A
C
D
E
F
证明:∵四边形ABCD
是平行四边形
∴∠A=∠C
(平行四边形对角相等)
AD=BC
(平行四边形对边相等)
∵DE⊥AB,BF⊥CD
∴∠AED=∠CFB=90°
在△AED和△CFB中
∠A=∠C
∠AED=∠CFB
AD=BC
∴△AED≌△CFB
(AAS)
∴AE=CF(全等三角形对应边相等)
例题讲解
1.如图:在
ABCD中,根据已知你能求出其它的边和角吗?说说你的理由
32cm
30cm
32cm
30cm
A
B
C
D
56°
56°
124°
124°
小试牛刀
1、已知
ABCD中,AB=8,BC=4,
其余各边长为多少?其周长等于多少?
A
B
C
D
2、已知
ABCD的周长是20,AB=6,
则BC=_
CD=__.
3、已知:
ABCD中,∠D=100°,你能求出
其他各角的度数吗?说说你的理由.
4、
中,∠A比∠B大30°,则∠A=_,∠D=__.
ABCD
小试牛刀
平行四边形的性质
边
平行四边形的对边平行且相等;
角
B
D
C
A
平行四边形的对角相等;
(邻角互补)
感悟与收获
https://www.21cnjy.com/help/help_extract.php
