2020-2021学年九年级数学人教版下册第27章第2节第1部分相似三角形的判定教案
文档属性
| 名称 | 2020-2021学年九年级数学人教版下册第27章第2节第1部分相似三角形的判定教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 364.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 00:00:00 | ||
图片预览


文档简介
27.2.1
相似三角形的判定
第1课时平行线分线段成比例
《平行线分线段成比例》是人教版九年级数学第二十七章《相似》第二节《相似三角形》第一课时的内容。它是在学生认识相似图形,了解相似多边形的性质及判定的基础上进行学习的。本课时首先复习相似多边形的性质,然后引出两个三角形相似的定义(即三个角分别相等,三条边成比例的两个三角形相似),然后引导学生思考类比全等三角形的判定方法,对于相似三角形是否存在较为简便的方法。接下来通过一个探究,由学生动手计算来探究得到平行线分线段成比例的基本事实(三条平行线截两条直线,所得的对应线段的比相等),从而将其应用于三角形中,得到“平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例”这一基本事实的推论,是进一步学习相似三角形判定的预备定理的基础。
●教学目标:
【知识与技能目标】
1、了解相似三角形的定义;
2、理解并掌握平行线分线段成比例的基本事实及其推论,并会灵活应用;
3、掌握两个三角形相似的预备定理.
【过程与方法目标】
经历“动手操作—直观感知—发现事实”的过程,增强学生发现问题,解决问题的能力.
【情感态度与价值观目标】
1、培养学生积极的思考、动手、观察的能力,使学生感悟几何知识在生活中的价值.
2、在进行探索的活动过程中,发展学生的探索发现归纳意识,并养成合作交流的学习习惯,体现数学的真善美.
●教学重点:判定两个三角形相似的预备定理
●教学难点:探究两个三角形相似的预备定理的过程
●教学过程设计:
一、复习提问,引入新课
问题1:什么是相似多边形?它具有什么性质?
师生活动:教师提出问题,学生思考并回答,使学生对上节课所学内容有深刻印象,以引起学生对本节课的研究内容的关注。
设计意图:通过对旧知识的复习和回顾,激发学生的学习兴趣,为学习新知识提供基础。
二、探索新知,自主学习
问题2:如何定义相似三角形?
问题3:如果k=1,则△ABC______△A'B'C'
师生活动:学生观察图形,结合相似多边形的定义,不难发现如果两个三角形的对应角相等,对应边成比例,那么这两个三角形相似。于是,得到判定三角形相似的定义:即对应角相等,对应边成比例的两个三角形叫相似三角形。教师适时提问,当相似比k为1时,这两个三角形又有怎样的关系?
在此活动中,教师应重点让学生关注和理解:
①相似的顺序性;②表示对应顶点的字母写在对应的位置上;③全等是特殊的相似,其相似比为1.
设计意图:通过观察,引导学生去探索、发现、归纳相似三角形的有关概念.
问题4:学习三角形全等时,我们知道,除了可以通过证明对应角相等,对应边相等来判定两个三角形全等外,还有判定的简便方法(SSS,SAS,ASA,AAS等).类似地,判定两个三角形相似时,是不是对所有的对应角和对应边都要一一验证呢?有没有简便方法呢?
师生活动:学生思考,并猜想判定方法,教师对学生的大胆猜想予以鼓励,并指出为了证明相似三角形的判定定理,我们先来学习下面的平行线分线段成比例这个基本事实.
设计意图:通过提问,引导学生回顾全等三角形的判定方法,并能类比全等三角形提出相似三角形判定方法的猜想.教师要关注学生的探究投入程度,鼓励学生大胆发表自己的见解.
三、问题探究,发现事实
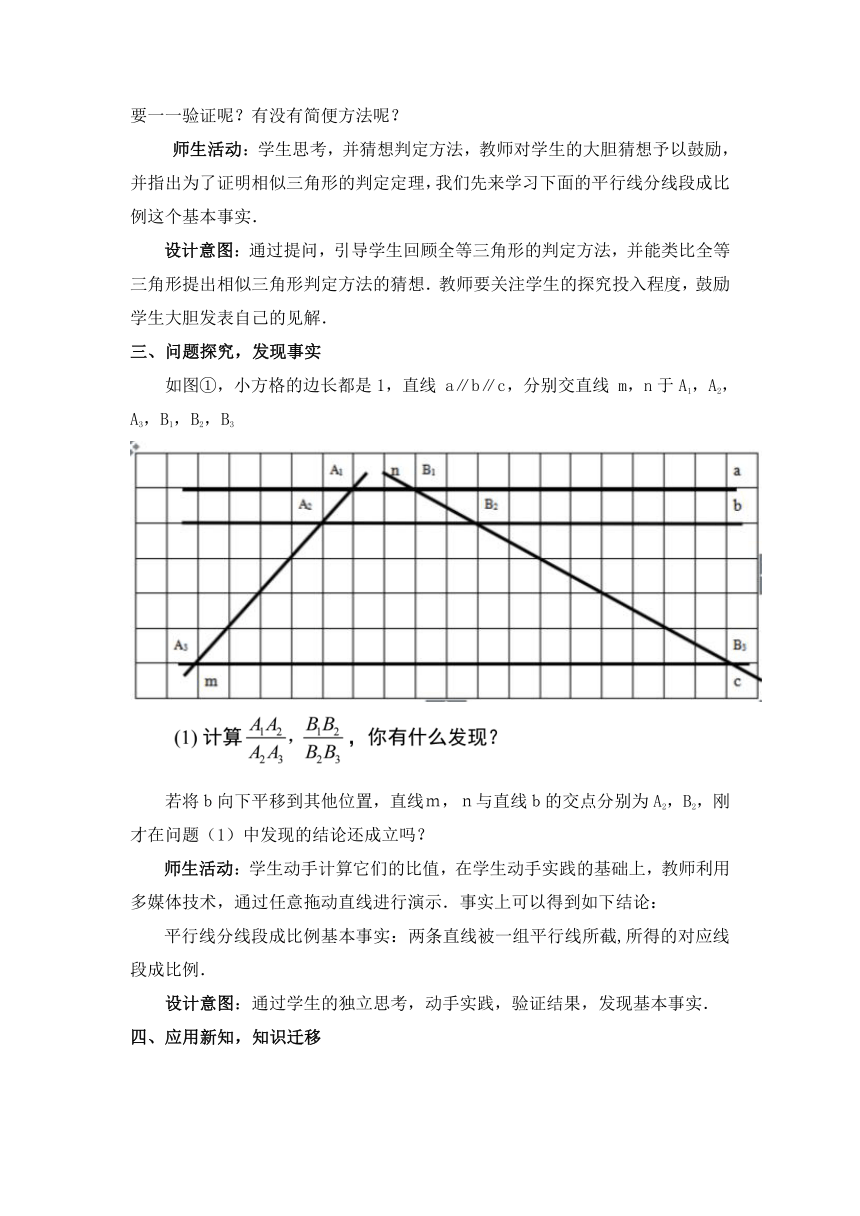
如图①,小方格的边长都是1,直线
a∥b∥c,分别交直线
m,n于A1,A2,A3,B1,B2,B3
若将b向下平移到其他位置,直线m,n与直线b的交点分别为A2,B2,刚才在问题(1)中发现的结论还成立吗?
师生活动:学生动手计算它们的比值,在学生动手实践的基础上,教师利用多媒体技术,通过任意拖动直线进行演示.事实上可以得到如下结论:
平行线分线段成比例基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
设计意图:通过学生的独立思考,动手实践,验证结果,发现基本事实.
四、应用新知,知识迁移
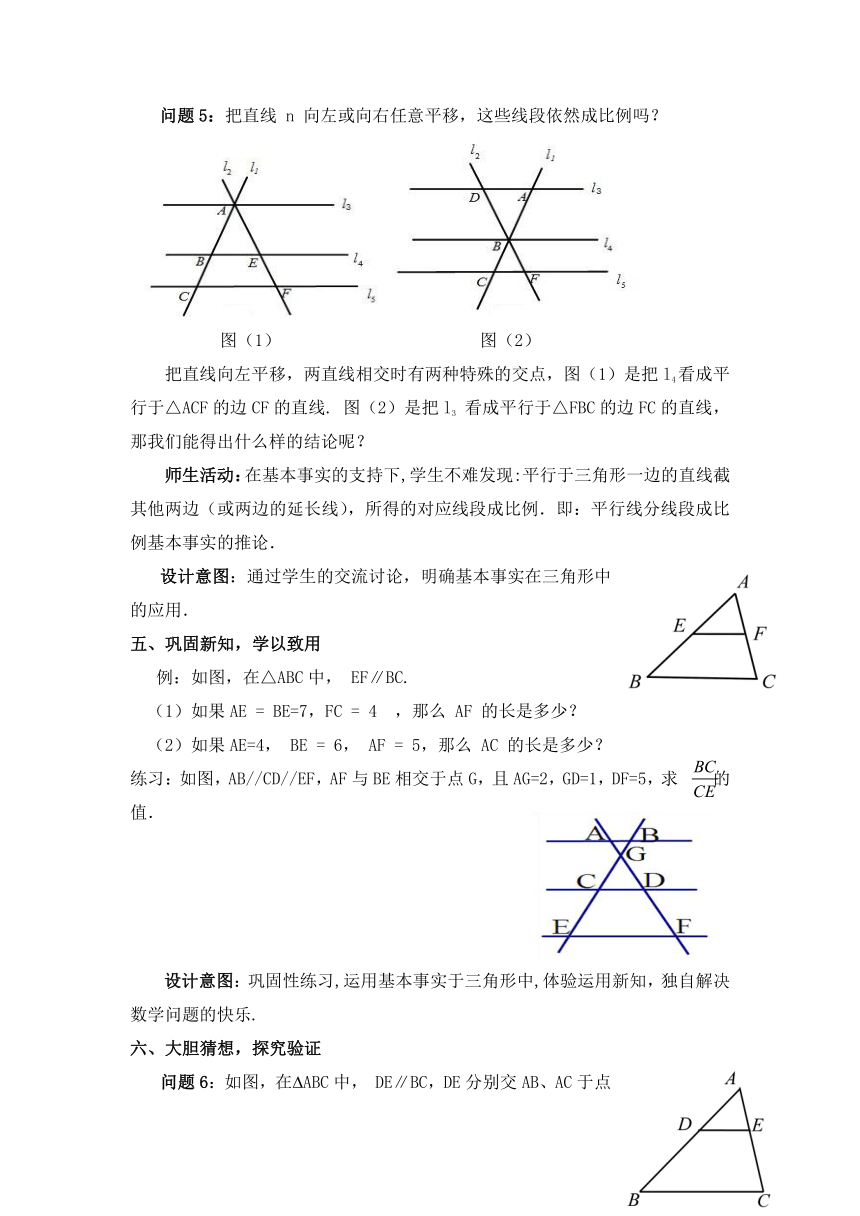
问题5:把直线
n
向左或向右任意平移,这些线段依然成比例吗?
图(1)
图(2)
把直线向左平移,两直线相交时有两种特殊的交点,图(1)是把l4看成平行于△ACF的边CF的直线.
图(2)是把l3
看成平行于△FBC的边FC的直线,那我们能得出什么样的结论呢?
师生活动:在基本事实的支持下,学生不难发现:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.即:平行线分线段成比例基本事实的推论.
设计意图:通过学生的交流讨论,明确基本事实在三角形中的应用.
五、巩固新知,学以致用
例:如图,在△ABC中,
EF∥BC.
(1)如果AE
=
BE=7,FC
=
4
,那么
AF
的长是多少?
(2)如果AE=4,
BE
=
6,
AF
=
5,那么
AC
的长是多少?
练习:如图,AB//CD//EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,求
的值.
设计意图:巩固性练习,运用基本事实于三角形中,体验运用新知,独自解决数学问题的快乐.
六、大胆猜想,探究验证
问题6:如图,在?ABC中,
DE∥BC,DE分别交AB、AC于点D、E
,?ADE与?ABC有什么关系?
师生活动:学生猜想:?ADE与?ABC相似,然后小组交流讨论,
如何验证猜想的成立?老师巡视给予指导。
证明:
归纳:平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似
设计意图:鼓励学生大胆猜想,培养学生的观察能力,善于发现问题,解决问题,善于总结的能力.
七、运用新知,巩固练习
1、已知:如图,AB∥EF∥CD,图中共有___对相似三角形.
2、若
△ABC
与
△A′B′C′
相似,一组对应边的长为AB
=3
cm,
A′B′=4
cm,那么△A′B′C′与
△ABC
的相似比是_____.
3、若
△ABC
的三条边长的比为3:5:6,与其相似的另一个
△A′B′C′
的最小边长为12
cm,那么
A′B′C′
的最大边长是______.
师生活动:学生独立思考并完成解答,教师点评.
设计意图:加深学生对新知识的理解,能灵活运用所学知识解决简单的问题,培养学生自主探索的精神.
八、随堂检测
师生活动:学生独立思考并完成解答,教师点评.
设计意图:加深了学生对本节课知识的巩固,让学生感受学习所收获到的成功喜悦。
九、课堂小结:
这节课有何收获?
学生活动:学生自由发言,交流学习的经验和体会,并自主总结本节课的主要内容。
设计意图:通过小结,使学生梳理本节课所学内容和探索问题的过程与方法,巩固平行线分线段成比例的基本事实及推论,两个三角形相似的预备定理.
十、布置作业
练习册P18-19
27.2.1相似三角形的判定第2课时教学设计
教学目标
知识技能
了解“三边成比例的两个三角形相似”和“两边成比例且夹角相等的两个三角形相似”判定定理的证明过程,能运用这两个判定定理证明三角形相似.
数学思考与问题解决
1.通过全等三角形的证明方法类比相似三角形的证明方法,在这个过程中渗透体会类比、转化的思想.
2.通过对相似三角形两个判定定理的学习,能根据已知条件证明三角形相似并解决一些简单的问题.
情感态度
通过全等三角形的SSS和SAS的证明方法,利用类比、转化的思想证明以上两个相似三角形的判定定理,在这个过程中,鼓励学生大胆猜想、模仿,培养学生的严谨推理能力.
重点难点
重点:能运用“三边成比例的两个三角形相似”和“两边成比例且夹角相等的两个三角形相似”的判定定理证明三角形相似.
难点:对“三边成比例的两个三角形相似”和“两边成比例且夹角相等的两个三角形相似”的判定定理的证明.
教学设计
活动一:问题情境
1.相似三角形是如何定义的呢?除了定义,还有什么方法可以判定相似三角形?
2.如果△ABC≌△A1B1C1,△A1B1C1∽△A2B2C2,那么△ABC和△A2B2C2有什么关系?
3.全等三角形又是如何定义的呢?我们证明全等三角形有哪些方法?(SSS,SAS,ASA,AAS,直角三角形还有HL)
4.全等三角形与相似三角形有什么关系?我们能否类比猜想,利用全等三角形的证明方法来判定三角形相似呢?
设计意图:问题1
是本课学习的知识基础,问题2是本课探究的依据,问题3和问题4是为本课的学习提供研究的方向,这些问题为本课学道路.
活动二:探索证明方法
1.如图1,如果用SSS判定三角形全等的方法,类比相似三角形的判定方法,在表述上有何区别?如何表述呢?
(在△ABC和△A1B1C1中,如果==,那么△ABC∽△A1B1C1.)
2.要证明这个结论,我们就应该在△ABC中,构造一个三角形,满足这个三角形与△ABC相似且与△A1B1C1全等,那么首先考虑这个三角形与△ABC相似,用已学的方法如何构造呢?(平行)
3.假设这条平行线DE∥BC,得到△ADE,可以证明△ADE∽△ABC,依据活动一问题2,接下来就应该满足△ADE≌△A1B1C1,那么你认为直线DE应该在什么位置呢?如何证明呢?(满足AD=A1B1)
4.类似地,如图2,如果用SAS判定三角形全等的方法,类比相似三角形的判定方法,在表述上有何区别?如何表述呢?并参照以上证明方法给出证明.
5.请你描述以上证明的两个结论,并依据图1和图2用数学符号表述出来.
设计意图:以问题教学形式,促进学生合理思考,改变教材直接呈现的结果,有利于学生猜想、联系、转化,直至证明.
活动三:精讲与精练
例1(教材第33页例1)
分析:(1)分析三边是否成比例即可;(2)分析夹角的两边是否成比例即可.
巩固练习1:教材第33页练习1,2,3.
设计意图:此环节的例题和习题难度都不大,让初学者有成就感,增加继续学习的信心.
活动四:提高与拓展
例2
已知:如图3,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.△ADQ与△QCP是否相似?为什么?
分析:容易发现△ADQ与△QCP都是直角三角形,有∠C=∠D=90°,下面只需证明夹∠D两边AD、DQ与夹∠C两边QC、PC对应成比例即可.
巩固练习2:如图4,四边形ABCD、四边形CDEF、四边形EFGH都是正方形.
(1)△ACF与△ACG相似吗?说说你的理由;
(2)求∠1+∠2的度数.
(答案:(1)相似,理由略;(2)45°.)
设计意图:此环节主要突出考查学生灵活掌握所学知识的能力,给学生更多的提供展示自己的舞台.
活动五:课堂小结与作业布置
1.课堂小结:(1)目前判定相似三角形有哪些方法?
(2)这些判定方法与全等三角形有何联系和区别?
2.作业布置:教材第42页第2(1),3,8题.
A
∽
相似三角形的判定
第1课时平行线分线段成比例
《平行线分线段成比例》是人教版九年级数学第二十七章《相似》第二节《相似三角形》第一课时的内容。它是在学生认识相似图形,了解相似多边形的性质及判定的基础上进行学习的。本课时首先复习相似多边形的性质,然后引出两个三角形相似的定义(即三个角分别相等,三条边成比例的两个三角形相似),然后引导学生思考类比全等三角形的判定方法,对于相似三角形是否存在较为简便的方法。接下来通过一个探究,由学生动手计算来探究得到平行线分线段成比例的基本事实(三条平行线截两条直线,所得的对应线段的比相等),从而将其应用于三角形中,得到“平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例”这一基本事实的推论,是进一步学习相似三角形判定的预备定理的基础。
●教学目标:
【知识与技能目标】
1、了解相似三角形的定义;
2、理解并掌握平行线分线段成比例的基本事实及其推论,并会灵活应用;
3、掌握两个三角形相似的预备定理.
【过程与方法目标】
经历“动手操作—直观感知—发现事实”的过程,增强学生发现问题,解决问题的能力.
【情感态度与价值观目标】
1、培养学生积极的思考、动手、观察的能力,使学生感悟几何知识在生活中的价值.
2、在进行探索的活动过程中,发展学生的探索发现归纳意识,并养成合作交流的学习习惯,体现数学的真善美.
●教学重点:判定两个三角形相似的预备定理
●教学难点:探究两个三角形相似的预备定理的过程
●教学过程设计:
一、复习提问,引入新课
问题1:什么是相似多边形?它具有什么性质?
师生活动:教师提出问题,学生思考并回答,使学生对上节课所学内容有深刻印象,以引起学生对本节课的研究内容的关注。
设计意图:通过对旧知识的复习和回顾,激发学生的学习兴趣,为学习新知识提供基础。
二、探索新知,自主学习
问题2:如何定义相似三角形?
问题3:如果k=1,则△ABC______△A'B'C'
师生活动:学生观察图形,结合相似多边形的定义,不难发现如果两个三角形的对应角相等,对应边成比例,那么这两个三角形相似。于是,得到判定三角形相似的定义:即对应角相等,对应边成比例的两个三角形叫相似三角形。教师适时提问,当相似比k为1时,这两个三角形又有怎样的关系?
在此活动中,教师应重点让学生关注和理解:
①相似的顺序性;②表示对应顶点的字母写在对应的位置上;③全等是特殊的相似,其相似比为1.
设计意图:通过观察,引导学生去探索、发现、归纳相似三角形的有关概念.
问题4:学习三角形全等时,我们知道,除了可以通过证明对应角相等,对应边相等来判定两个三角形全等外,还有判定的简便方法(SSS,SAS,ASA,AAS等).类似地,判定两个三角形相似时,是不是对所有的对应角和对应边都要一一验证呢?有没有简便方法呢?
师生活动:学生思考,并猜想判定方法,教师对学生的大胆猜想予以鼓励,并指出为了证明相似三角形的判定定理,我们先来学习下面的平行线分线段成比例这个基本事实.
设计意图:通过提问,引导学生回顾全等三角形的判定方法,并能类比全等三角形提出相似三角形判定方法的猜想.教师要关注学生的探究投入程度,鼓励学生大胆发表自己的见解.
三、问题探究,发现事实
如图①,小方格的边长都是1,直线
a∥b∥c,分别交直线
m,n于A1,A2,A3,B1,B2,B3
若将b向下平移到其他位置,直线m,n与直线b的交点分别为A2,B2,刚才在问题(1)中发现的结论还成立吗?
师生活动:学生动手计算它们的比值,在学生动手实践的基础上,教师利用多媒体技术,通过任意拖动直线进行演示.事实上可以得到如下结论:
平行线分线段成比例基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
设计意图:通过学生的独立思考,动手实践,验证结果,发现基本事实.
四、应用新知,知识迁移
问题5:把直线
n
向左或向右任意平移,这些线段依然成比例吗?
图(1)
图(2)
把直线向左平移,两直线相交时有两种特殊的交点,图(1)是把l4看成平行于△ACF的边CF的直线.
图(2)是把l3
看成平行于△FBC的边FC的直线,那我们能得出什么样的结论呢?
师生活动:在基本事实的支持下,学生不难发现:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.即:平行线分线段成比例基本事实的推论.
设计意图:通过学生的交流讨论,明确基本事实在三角形中的应用.
五、巩固新知,学以致用
例:如图,在△ABC中,
EF∥BC.
(1)如果AE
=
BE=7,FC
=
4
,那么
AF
的长是多少?
(2)如果AE=4,
BE
=
6,
AF
=
5,那么
AC
的长是多少?
练习:如图,AB//CD//EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,求
的值.
设计意图:巩固性练习,运用基本事实于三角形中,体验运用新知,独自解决数学问题的快乐.
六、大胆猜想,探究验证
问题6:如图,在?ABC中,
DE∥BC,DE分别交AB、AC于点D、E
,?ADE与?ABC有什么关系?
师生活动:学生猜想:?ADE与?ABC相似,然后小组交流讨论,
如何验证猜想的成立?老师巡视给予指导。
证明:
归纳:平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似
设计意图:鼓励学生大胆猜想,培养学生的观察能力,善于发现问题,解决问题,善于总结的能力.
七、运用新知,巩固练习
1、已知:如图,AB∥EF∥CD,图中共有___对相似三角形.
2、若
△ABC
与
△A′B′C′
相似,一组对应边的长为AB
=3
cm,
A′B′=4
cm,那么△A′B′C′与
△ABC
的相似比是_____.
3、若
△ABC
的三条边长的比为3:5:6,与其相似的另一个
△A′B′C′
的最小边长为12
cm,那么
A′B′C′
的最大边长是______.
师生活动:学生独立思考并完成解答,教师点评.
设计意图:加深学生对新知识的理解,能灵活运用所学知识解决简单的问题,培养学生自主探索的精神.
八、随堂检测
师生活动:学生独立思考并完成解答,教师点评.
设计意图:加深了学生对本节课知识的巩固,让学生感受学习所收获到的成功喜悦。
九、课堂小结:
这节课有何收获?
学生活动:学生自由发言,交流学习的经验和体会,并自主总结本节课的主要内容。
设计意图:通过小结,使学生梳理本节课所学内容和探索问题的过程与方法,巩固平行线分线段成比例的基本事实及推论,两个三角形相似的预备定理.
十、布置作业
练习册P18-19
27.2.1相似三角形的判定第2课时教学设计
教学目标
知识技能
了解“三边成比例的两个三角形相似”和“两边成比例且夹角相等的两个三角形相似”判定定理的证明过程,能运用这两个判定定理证明三角形相似.
数学思考与问题解决
1.通过全等三角形的证明方法类比相似三角形的证明方法,在这个过程中渗透体会类比、转化的思想.
2.通过对相似三角形两个判定定理的学习,能根据已知条件证明三角形相似并解决一些简单的问题.
情感态度
通过全等三角形的SSS和SAS的证明方法,利用类比、转化的思想证明以上两个相似三角形的判定定理,在这个过程中,鼓励学生大胆猜想、模仿,培养学生的严谨推理能力.
重点难点
重点:能运用“三边成比例的两个三角形相似”和“两边成比例且夹角相等的两个三角形相似”的判定定理证明三角形相似.
难点:对“三边成比例的两个三角形相似”和“两边成比例且夹角相等的两个三角形相似”的判定定理的证明.
教学设计
活动一:问题情境
1.相似三角形是如何定义的呢?除了定义,还有什么方法可以判定相似三角形?
2.如果△ABC≌△A1B1C1,△A1B1C1∽△A2B2C2,那么△ABC和△A2B2C2有什么关系?
3.全等三角形又是如何定义的呢?我们证明全等三角形有哪些方法?(SSS,SAS,ASA,AAS,直角三角形还有HL)
4.全等三角形与相似三角形有什么关系?我们能否类比猜想,利用全等三角形的证明方法来判定三角形相似呢?
设计意图:问题1
是本课学习的知识基础,问题2是本课探究的依据,问题3和问题4是为本课的学习提供研究的方向,这些问题为本课学道路.
活动二:探索证明方法
1.如图1,如果用SSS判定三角形全等的方法,类比相似三角形的判定方法,在表述上有何区别?如何表述呢?
(在△ABC和△A1B1C1中,如果==,那么△ABC∽△A1B1C1.)
2.要证明这个结论,我们就应该在△ABC中,构造一个三角形,满足这个三角形与△ABC相似且与△A1B1C1全等,那么首先考虑这个三角形与△ABC相似,用已学的方法如何构造呢?(平行)
3.假设这条平行线DE∥BC,得到△ADE,可以证明△ADE∽△ABC,依据活动一问题2,接下来就应该满足△ADE≌△A1B1C1,那么你认为直线DE应该在什么位置呢?如何证明呢?(满足AD=A1B1)
4.类似地,如图2,如果用SAS判定三角形全等的方法,类比相似三角形的判定方法,在表述上有何区别?如何表述呢?并参照以上证明方法给出证明.
5.请你描述以上证明的两个结论,并依据图1和图2用数学符号表述出来.
设计意图:以问题教学形式,促进学生合理思考,改变教材直接呈现的结果,有利于学生猜想、联系、转化,直至证明.
活动三:精讲与精练
例1(教材第33页例1)
分析:(1)分析三边是否成比例即可;(2)分析夹角的两边是否成比例即可.
巩固练习1:教材第33页练习1,2,3.
设计意图:此环节的例题和习题难度都不大,让初学者有成就感,增加继续学习的信心.
活动四:提高与拓展
例2
已知:如图3,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.△ADQ与△QCP是否相似?为什么?
分析:容易发现△ADQ与△QCP都是直角三角形,有∠C=∠D=90°,下面只需证明夹∠D两边AD、DQ与夹∠C两边QC、PC对应成比例即可.
巩固练习2:如图4,四边形ABCD、四边形CDEF、四边形EFGH都是正方形.
(1)△ACF与△ACG相似吗?说说你的理由;
(2)求∠1+∠2的度数.
(答案:(1)相似,理由略;(2)45°.)
设计意图:此环节主要突出考查学生灵活掌握所学知识的能力,给学生更多的提供展示自己的舞台.
活动五:课堂小结与作业布置
1.课堂小结:(1)目前判定相似三角形有哪些方法?
(2)这些判定方法与全等三角形有何联系和区别?
2.作业布置:教材第42页第2(1),3,8题.
A
∽
