2020-2021学年七年级数学人教版下册第5章第2节第2部分平行线的判定教案 (1)
文档属性
| 名称 | 2020-2021学年七年级数学人教版下册第5章第2节第2部分平行线的判定教案 (1) |
|
|
| 格式 | zip | ||
| 文件大小 | 201.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 00:00:00 | ||
图片预览

文档简介
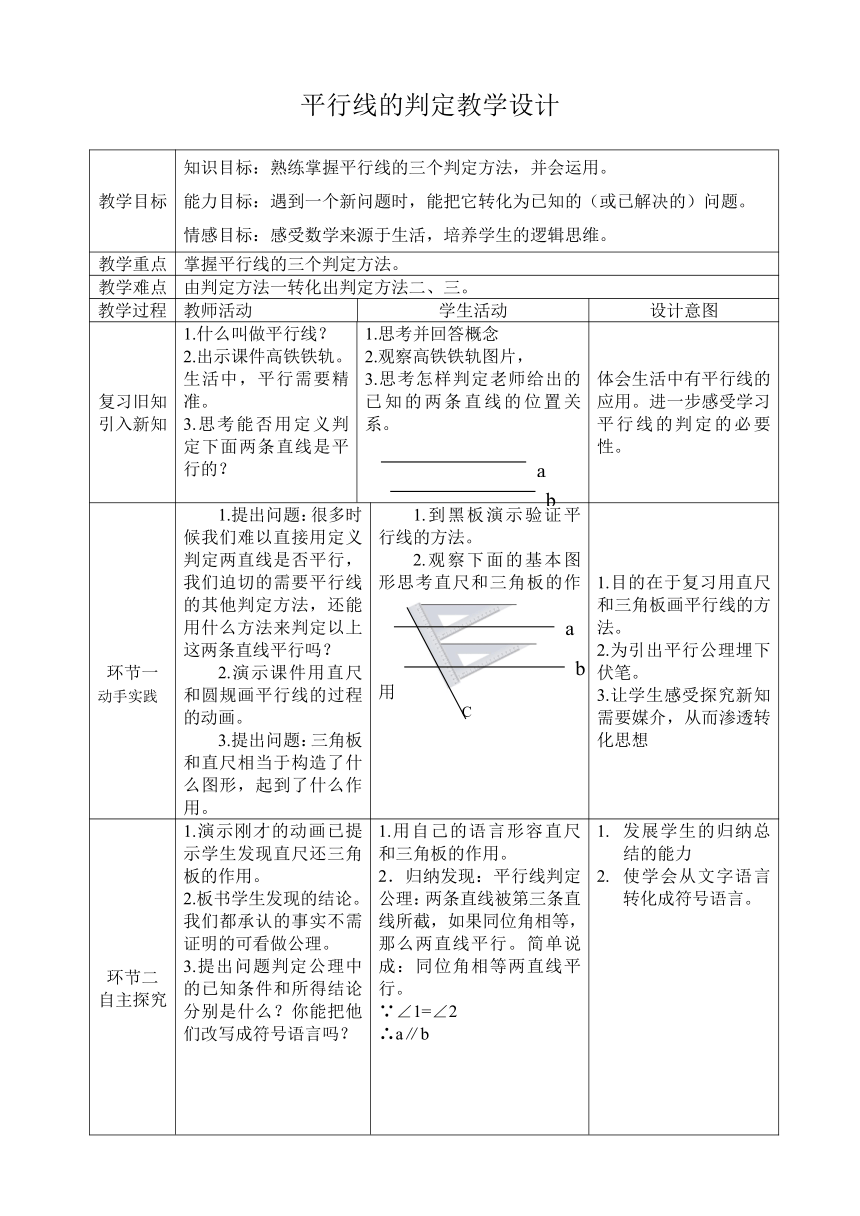
平行线的判定教学设计
教学目标
知识目标:熟练掌握平行线的三个判定方法,并会运用。
能力目标:遇到一个新问题时,能把它转化为已知的(或已解决的)问题。
情感目标:感受数学来源于生活,培养学生的逻辑思维。
教学重点
掌握平行线的三个判定方法。
教学难点
由判定方法一转化出判定方法二、三。
教学过程
教师活动
学生活动
设计意图
复习旧知引入新知
1.什么叫做平行线?2.出示课件高铁铁轨。生活中,平行需要精准。3.思考能否用定义判定下面两条直线是平行的?
1.思考并回答概念2.观察高铁铁轨图片,3.思考怎样判定老师给出的已知的两条直线的位置关系。
体会生活中有平行线的应用。进一步感受学习平行线的判定的必要性。
环节一动手实践
1.提出问题:很多时候我们难以直接用定义判定两直线是否平行,我们迫切的需要平行线的其他判定方法,还能用什么方法来判定以上这两条直线平行吗?2.演示课件用直尺和圆规画平行线的过程的动画。3.提出问题:三角板和直尺相当于构造了什么图形,起到了什么作用。
1.到黑板演示验证平行线的方法。2.观察下面的基本图形思考直尺和三角板的作用
1.目的在于复习用直尺和三角板画平行线的方法。2.为引出平行公理埋下伏笔。3.让学生感受探究新知需要媒介,从而渗透转化思想
环节二自主探究
1.演示刚才的动画已提示学生发现直尺还三角板的作用。2.板书学生发现的结论。我们都承认的事实不需证明的可看做公理。3.提出问题判定公理中的已知条件和所得结论分别是什么?你能把他们改写成符号语言吗?4.练习:如图,∠1=∠2,AB
与CD平行吗?为什么?
1.用自己的语言形容直尺和三角板的作用。2.归纳发现:平行线判定公理:两条直线被第三条直线所截,如果同位角相等,那么两直线平行。简单说成:同位角相等两直线平行。∵∠1=∠2∴a∥b完成证明过程,体会证明平行时判定方法一的应用。
发展学生的归纳总结的能力使学会从文字语言转化成符号语言。1.让学生体会怎样由已知条件向判定方法的条件转化。怎样将转化思想在问题中实践。2.意在突破本节课的难点:证明判定方法二和判定方法三时都是向判定一转化。
环节三展示交流
1.组织学生小组内及组与组之间合作,讨论其他的判定方法。猜想并证明。教师巡回在学生之间,听取各小组学生意见和讨论交流的结果,同时可以适时给予指导。2.总结判定2:内错角相等两直线平行。和判定
3:同旁内角互补两直线平行。并引导学生体会转化思想。3.引导学生分析三种判定方法易错点。
小组选派代表展示交流结果,有不完善的地方小组其它成员补充完成。发现证明判定2时是将条件转化成同位角相等,证明判定三是是将条件转化成同位角相等或是内错角相等。利用同旁内角判定时要找互补而不是相等关系。
学生小组合作,发挥集体力量解决学习中存在的疑惑,培养学生团结协作的精神及解决问题的能力,激发学生学习数学的热情。体会转化思想为学生能独立思考问题提供方法。培养孩子扎实的学习习惯。比较是使印象深刻的好方法。
环节四实践提升环节五拓展延伸
例1
如图,你能说出木工用图中的角尺画平行线的道理吗?
例2.①如果∠1=∠2,能判定哪两条直线平行?为什么?
②如果∠1=∠3,能判定哪两条直线平行?为什么?
③如果∠A+∠
ABC=180?
,能判定哪两条直线平行?为什么?1.如图,
BE是AB的延长线.1)满足什么条件可以判定AD∥BC.并说明理由
(2)满足什么条件可以判定DC∥AE.并说明理由2.已知:如图,四边形ABCD中,AC平分∠BAD,∠1=∠2,AB与CD平行吗?为什么?
例1让学生体会知识在生活中的应用。并培养学生语言表达能力及数学思维能力。例2训练在复杂图形中平行线判定方法的使用。体会三线八角图是基础。开放性问题,拓展学生的思维宽度。同一组平行线被不同的截线所截形成不同的角利用不用的判定方法。2.
条件复杂的综合性问题使学生形成较长的思维连。
环节六总结升华
数形结合学平行,利用数量判位置;判定公理做基础,逐步转化引新知;三线八角是基本,平行线是被截线;若是条件不直接,尽你所能再转化。
使学生加深对本节课内容整体的把握。培养总结归纳的能力。
a
b
a
b
C
2
1
F
E
D
C
B
A
教学目标
知识目标:熟练掌握平行线的三个判定方法,并会运用。
能力目标:遇到一个新问题时,能把它转化为已知的(或已解决的)问题。
情感目标:感受数学来源于生活,培养学生的逻辑思维。
教学重点
掌握平行线的三个判定方法。
教学难点
由判定方法一转化出判定方法二、三。
教学过程
教师活动
学生活动
设计意图
复习旧知引入新知
1.什么叫做平行线?2.出示课件高铁铁轨。生活中,平行需要精准。3.思考能否用定义判定下面两条直线是平行的?
1.思考并回答概念2.观察高铁铁轨图片,3.思考怎样判定老师给出的已知的两条直线的位置关系。
体会生活中有平行线的应用。进一步感受学习平行线的判定的必要性。
环节一动手实践
1.提出问题:很多时候我们难以直接用定义判定两直线是否平行,我们迫切的需要平行线的其他判定方法,还能用什么方法来判定以上这两条直线平行吗?2.演示课件用直尺和圆规画平行线的过程的动画。3.提出问题:三角板和直尺相当于构造了什么图形,起到了什么作用。
1.到黑板演示验证平行线的方法。2.观察下面的基本图形思考直尺和三角板的作用
1.目的在于复习用直尺和三角板画平行线的方法。2.为引出平行公理埋下伏笔。3.让学生感受探究新知需要媒介,从而渗透转化思想
环节二自主探究
1.演示刚才的动画已提示学生发现直尺还三角板的作用。2.板书学生发现的结论。我们都承认的事实不需证明的可看做公理。3.提出问题判定公理中的已知条件和所得结论分别是什么?你能把他们改写成符号语言吗?4.练习:如图,∠1=∠2,AB
与CD平行吗?为什么?
1.用自己的语言形容直尺和三角板的作用。2.归纳发现:平行线判定公理:两条直线被第三条直线所截,如果同位角相等,那么两直线平行。简单说成:同位角相等两直线平行。∵∠1=∠2∴a∥b完成证明过程,体会证明平行时判定方法一的应用。
发展学生的归纳总结的能力使学会从文字语言转化成符号语言。1.让学生体会怎样由已知条件向判定方法的条件转化。怎样将转化思想在问题中实践。2.意在突破本节课的难点:证明判定方法二和判定方法三时都是向判定一转化。
环节三展示交流
1.组织学生小组内及组与组之间合作,讨论其他的判定方法。猜想并证明。教师巡回在学生之间,听取各小组学生意见和讨论交流的结果,同时可以适时给予指导。2.总结判定2:内错角相等两直线平行。和判定
3:同旁内角互补两直线平行。并引导学生体会转化思想。3.引导学生分析三种判定方法易错点。
小组选派代表展示交流结果,有不完善的地方小组其它成员补充完成。发现证明判定2时是将条件转化成同位角相等,证明判定三是是将条件转化成同位角相等或是内错角相等。利用同旁内角判定时要找互补而不是相等关系。
学生小组合作,发挥集体力量解决学习中存在的疑惑,培养学生团结协作的精神及解决问题的能力,激发学生学习数学的热情。体会转化思想为学生能独立思考问题提供方法。培养孩子扎实的学习习惯。比较是使印象深刻的好方法。
环节四实践提升环节五拓展延伸
例1
如图,你能说出木工用图中的角尺画平行线的道理吗?
例2.①如果∠1=∠2,能判定哪两条直线平行?为什么?
②如果∠1=∠3,能判定哪两条直线平行?为什么?
③如果∠A+∠
ABC=180?
,能判定哪两条直线平行?为什么?1.如图,
BE是AB的延长线.1)满足什么条件可以判定AD∥BC.并说明理由
(2)满足什么条件可以判定DC∥AE.并说明理由2.已知:如图,四边形ABCD中,AC平分∠BAD,∠1=∠2,AB与CD平行吗?为什么?
例1让学生体会知识在生活中的应用。并培养学生语言表达能力及数学思维能力。例2训练在复杂图形中平行线判定方法的使用。体会三线八角图是基础。开放性问题,拓展学生的思维宽度。同一组平行线被不同的截线所截形成不同的角利用不用的判定方法。2.
条件复杂的综合性问题使学生形成较长的思维连。
环节六总结升华
数形结合学平行,利用数量判位置;判定公理做基础,逐步转化引新知;三线八角是基本,平行线是被截线;若是条件不直接,尽你所能再转化。
使学生加深对本节课内容整体的把握。培养总结归纳的能力。
a
b
a
b
C
2
1
F
E
D
C
B
A
