2020-2021学年七年级数学苏科版下册 第七章 平面的图形认识(二)解答题专项提升(一)(Word版,附答案)
文档属性
| 名称 | 2020-2021学年七年级数学苏科版下册 第七章 平面的图形认识(二)解答题专项提升(一)(Word版,附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 218.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 16:12:49 | ||
图片预览


文档简介
苏科版七年级下册数学
第七章
平面的图形认识(二)
解答题专项提升(一)
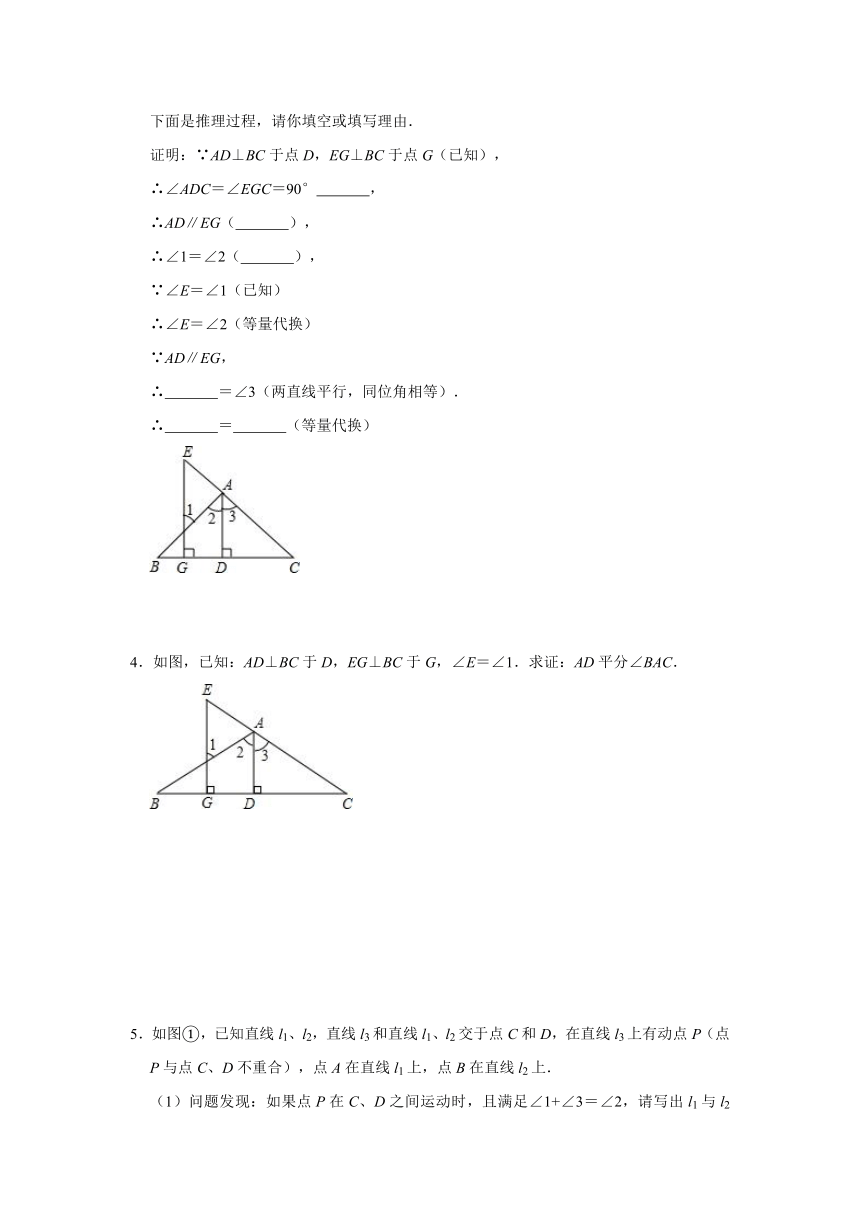
1.如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F.
(1)∠ABC=40°,∠A=60°,求∠BFD的度数;
(2)直接写出∠A与∠BFD的数量关系.
2.如图1,在四边形ABCD中,∠ABC+∠ADC=180°,BE、DF分别是∠ABC与∠ADC的平分线,∠ADF与∠AFD互余.
(1)试判断直线BE与DF的位置关系,并说明理由;
(2)如图2,延长CB、DF相交于点G,过点B作BH⊥FG,垂足为点H,试判断∠FBH与∠GBH的大小关系,并说明理由.
3.如图所示,AD⊥BC于点D,EG⊥BC于点G,若∠E=∠1,则∠2=∠3吗?
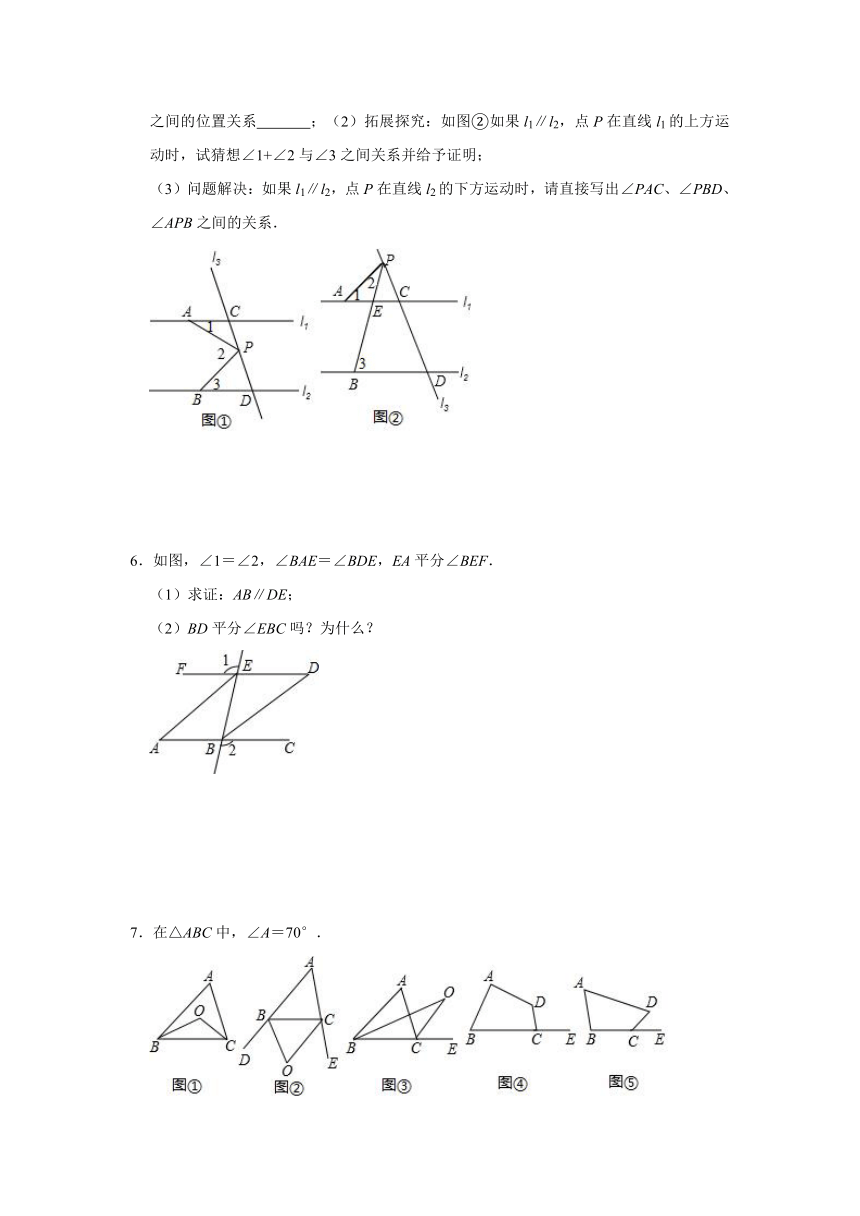
下面是推理过程,请你填空或填写理由.
证明:∵AD⊥BC于点D,EG⊥BC于点G(已知),
∴∠ADC=∠EGC=90°
,
∴AD∥EG(
),
∴∠1=∠2(
),
∵∠E=∠1(已知)
∴∠E=∠2(等量代换)
∵AD∥EG,
∴
=∠3(两直线平行,同位角相等).
∴
=
(等量代换)
4.如图,已知:AD⊥BC于D,EG⊥BC于G,∠E=∠1.求证:AD平分∠BAC.
5.如图①,已知直线l1、l2,直线l3和直线l1、l2交于点C和D,在直线l3上有动点P(点P与点C、D不重合),点A在直线l1上,点B在直线l2上.
(1)问题发现:如果点P在C、D之间运动时,且满足∠1+∠3=∠2,请写出l1与l2之间的位置关系
;(2)拓展探究:如图②如果l1∥l2,点P在直线l1的上方运动时,试猜想∠1+∠2与∠3之间关系并给予证明;
(3)问题解决:如果l1∥l2,点P在直线l2的下方运动时,请直接写出∠PAC、∠PBD、∠APB之间的关系.
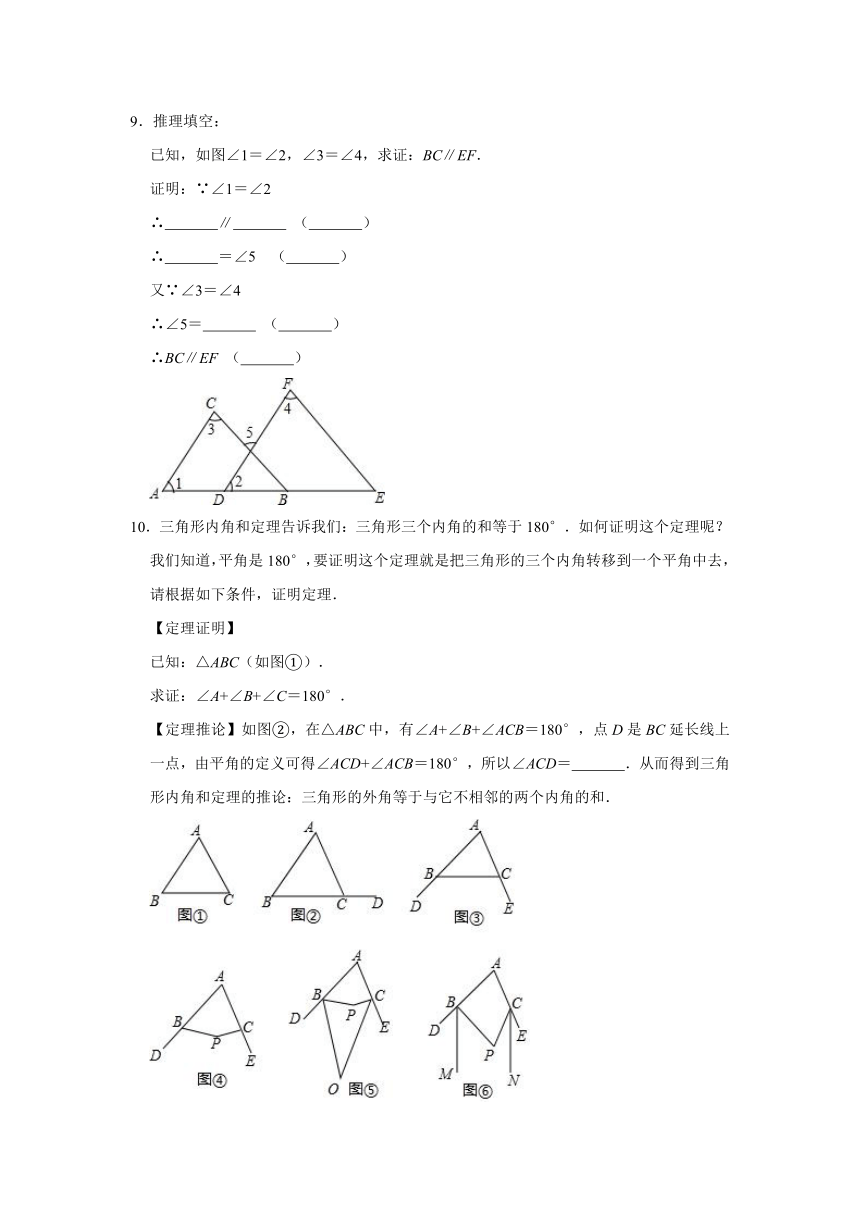
6.如图,∠1=∠2,∠BAE=∠BDE,EA平分∠BEF.
(1)求证:AB∥DE;
(2)BD平分∠EBC吗?为什么?
7.在△ABC中,∠A=70°.
(1)如图①∠ABC,∠ACB
的平分线相交于点O,则∠BOC=
°;
(2)如图②△ABC的外角∠CBD,∠BCE
的平分线相交于点O',则∠BO'C=
°;
(3)探究
探究一:如图③,△ABC的内角∠ABC的平分线与其外角∠ACD
的平分线相交于点O,设∠A=n°,求∠BOC的度数.(用n的代数式表示)
探究二:已知:四边形ABCD的内角∠ABC的平分线所在直线与其外角∠DCE的平分线所在直线
相交于点O,∠A=n°,∠D=m°
①如图④,若∠A+∠D≥180°,则∠BOC=
(用m、n的代数式表示)
②如图⑤,若∠A+∠D<180°,则∠BOC=
(用m、n的代数式表示)
8.若∠C=α,∠EAC+∠FBC=β
(1)如图①,AM是∠EAC的平分线,BN是∠FBC的平分线,若AM∥BN,则α与β有何关系?并说明理由.
(2)如图②,若∠EAC的平分线所在直线与∠FBC平分线所在直线交于P,试探究∠APB与α、β的关系是
.(用α、β表示)
(3)如图③,若α≥β,∠EAC与∠FBC的平分线相交于P1,∠EAP1与∠FBP1的平分线交于P2;依此类推,则∠P5=
.(用α、β表示)
9.推理填空:
已知,如图∠1=∠2,∠3=∠4,求证:BC∥EF.
证明:∵∠1=∠2
∴
∥
(
)
∴
=∠5
(
)
又∵∠3=∠4
∴∠5=
(
)
∴BC∥EF
(
)
10.三角形内角和定理告诉我们:三角形三个内角的和等于180°.如何证明这个定理呢?
我们知道,平角是180°,要证明这个定理就是把三角形的三个内角转移到一个平角中去,请根据如下条件,证明定理.
【定理证明】
已知:△ABC(如图①).
求证:∠A+∠B+∠C=180°.
【定理推论】如图②,在△ABC中,有∠A+∠B+∠ACB=180°,点D是BC延长线上一点,由平角的定义可得∠ACD+∠ACB=180°,所以∠ACD=
.从而得到三角形内角和定理的推论:三角形的外角等于与它不相邻的两个内角的和.
【初步运用】如图③,点D、E分别是△ABC的边AB、AC延长线上一点.
(1)若∠A=80°,∠DBC=150°,则∠ACB=
°;
(2)若∠A=80°,则∠DBC+∠ECB=
°.
【拓展延伸】如图④,点D、E分别是四边形ABPC的边AB、AC延长线上一点.
(1)若∠A=80°,∠P=150°,则∠DBP+∠ECP=
°;
(2)分别作∠DBP和∠ECP的平分线,交于点O,如图⑤,若∠O=50°,则∠A和∠P的数量关系为
;
(3)分别作∠DBP和∠ECP的平分线BM、CN,如图⑥,若∠A=∠P,求证:BM∥CN.
11.如图,在△ABC中,∠BAC=40°,∠ACB=75°,点I是两条角平分线的交点.
(1)求∠BIC的度数;
(2)若点D是两条外角平分线的交点,求∠BDC的度数;
(3)若点E是内角∠ABC、外角∠ACG的平分线交点,试探索∠BEC与∠BAC的数量关系,并说明理由.
12.已知:在△ABC和△DEF中,∠A=36°,∠E+∠F=100°,将△DEF如图放置,使得∠D的两条边分别经过点B和点C.
(1)当将△DEF如图1摆放时,∠ABF+∠ACE=
°.
(2)当将△DEF如图2摆放时,试问:∠ABF+∠ACE等于多少度?请说明理由.
(3)如图2,是否存在将△DEF摆放到某个位置时,使得BD,CD分别平分∠ABC和∠ACB?如果存在,请画出图形或说明理由.如果不存在,请改变题目中的一个已知条件,使之存在.
13.如图①,在△ABC中,∠B=∠C,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连接DE.
(1)若∠BAC=100°,∠DAE=40°,则∠CDE=
,此时=
;
(2)若点D在BC边上(点B、C除外)运动,试探究∠BAD与∠CDE的数量关系并说明理由;
(3)若点D在线段BC的延长线上,点E在线段AC的延长线上(如图②),其余条件不变,请直接写出∠BAD与∠CDE的数量关系:
;
(4)若点D在线段CB的延长线上(如图③)、点E在直线AC上,∠BAD=26°,其余条件不变,则∠CDE=
°(友情提醒:可利用图③画图分析)
14.已知:如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC,且∠1=∠3.说明AB∥DC的理由.
解:∵∠ABC=∠ADC,
∴∠ABC=∠ADC
又∵BF、DE分别平分∠ABC与∠ADC,
∴∠1=ABC,∠2=∠ADC
∴∠
=∠
.(等量代换)
∵∠1=∠3,
∴∠2=
.
∴
∥
.
.
15.已知:CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
(1)如图1,求证∠BAC=∠B+2∠E;
(2)如图2,过点A作AF⊥BC,垂足为点F,若∠DCE=2∠CAF,∠B=2∠E,求∠BAC的度数.
参考答案
1.解:(1)∵∠ABC=40°,∠A=60°,
∴∠ACB=180°﹣40°﹣60°=80°,
∵∠B、∠C的平分线BE,CD相交于点F,
∴∠BFD=∠FBC+∠FCB=∠ABC+∠ACB=20°+40°=60°.
(2)∵∠B、∠C的平分线BE,CD相交于点F,
∴∠BFD=∠FBC+∠FCB=∠ABC+∠ACB=(∠ABC+∠ACB)=(180°﹣∠A)=90°﹣∠A.
2.解:(1)BE∥DF,
理由:∵BE、DF分别是∠ABC与∠ADC的平分线,
∴∠ABE=∠CBE=∠ABC,∠ADF=∠CDF=∠ADC,
∵∠ABC+∠ADC=180°,
∴∠ABE+∠ADF=90°,
∵∠ADF与∠AFD互余,
∴∠ADF+∠AFD=90°,
∴∠ABE=∠AFD,
∴BE∥DF;
(2)∠FBH=∠GBH,
理由:由(1)知BE∥DF,
∴BE∥DG,
∴∠EBH+∠DHB=180°,
∵BH⊥FG,
∴∠DHB=90°,
∴∠EBH=180°﹣∠DHB=90°.
∴∠CBE+∠GBH=180°﹣∠EBH=90°,
∵∠ABE+∠ABH=∠EBH=90°,
∵∠ABE=∠CBE,
∴∠ABH=∠GBH,
即∠FBH=∠GBH.
3.证明:∵AD⊥BC于点D,EG⊥BC于点G(已知),
∴∠ADC=∠EGC=90°(垂直的定义),
∴AD∥EG(同位角相等,两直线平行),
∴∠1=∠2(两直线平行,内错角相等),
∵∠E=∠1(已知)
∴∠E=∠2(等量代换)
∵AD∥EG,
∴∠E=∠3(两直线平行,同位角相等).
∴∠2=∠3(等量代换),
故答案为:垂直的定义,同位角相等,两直线平行,两直线平行,同位角相等,∠E,∠2,∠3.
4.证明:∵AD⊥BC于D,EG⊥BC于G,(已知)
∴∠ADC=∠EGC=90°,
∴AD∥EG,(同位角相等,两直线平行).
∴∠1=∠2,(两直线平行,内错角相等).
∠E=∠3(两直线平行,同位角相等)
又∵∠E=∠1(已知)
∴∠2=∠3,(等量代换).
∴AD平分∠BAC.(角平分线的定义)
5.证明:(1)如图①,延长BP交AC于E,
∵∠2=∠1+∠3,∠2=∠1+∠AEP,
∴∠3=∠AEP,
∴l1∥l2,
故答案为:l1∥l2;
(2)如图②所示,当点P在线段DC的延长线上时,∠1+∠2=∠3,
理由是:∵l1∥l2,
∴∠CEP=∠3
∵∠CEP=∠1+∠2,
∴∠1+∠2=∠3;
(3)如图③所示,当点P在直线l2的下方运动时,∠APB+∠PBD=∠PAC.
理由:过点P作PF∥l1,
∠FPA=∠1.
∵l1∥l2,
∴PF∥l2,
∴∠FPB=∠3,
∴∠FPA=∠2+∠FPB=∠2+∠3;
即∠APB+∠PBD=∠PAC.
6.(1)证明:∵∠2与∠ABE是对顶角,
∴∠2=∠ABE.
∵∠1=∠2,
∴∠1=∠ABE,
∴AB∥DE;
(2)解:BD平分∠EBC.
理由:∵由(1)知AB∥CD,
∴∠AED+∠BAE=180°,∠BEF=∠EBC.
∵∠BAE=∠BDE,
∴∠AED+∠BDE=180°,
∴AE∥BD,
∴∠AEB=∠DBE.
∵EA平分∠BEF,∠BEF=∠EBC,
∴BD平分∠EBC.
7.解:(1)∵∠A=70°,
∴∠ABC+∠ACB=180°﹣∠A=110°,
∵BO、CO分别是∠ABC和∠ACB的平分线,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=×110°=55°,
∴在△BOC中,∠BOC=180°﹣(∠OBC+∠OCB)=125°;
(2)∵∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC,
∴∠DBC+∠ECB=∠A+∠ACB+∠A+∠ABC=180°+∠A,
∵BO、CO分别是△ABC两个外角∠CBD和∠BCE的平分线,
∴∠OBC=∠DBC,∠OCB=∠ECB,
∴∠OBC+∠OCB=(180°+∠A),
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(180°+∠A)=90°﹣∠A=55°;
(3)探究
探究一:∵BO和CO分别是∠ABC和∠ACD的角平分线,
∴∠OBC=∠ABC,∠OCE=∠ACD,
又∵∠ACD是△ABC的一外角,
∴∠ACD=∠A+∠ABC,
∴∠OCE=(∠A+∠ABC)=∠A+∠OBC,
∵∠OCE是△BOC的一外角,
∴∠BOC=∠OCE﹣∠OBC=∠A+∠OBC﹣∠OBC=∠A=n°;
探究二:①由四边形内角和定理得,∠BCD=360°﹣∠A﹣∠D﹣∠ABC,
∴∠DCE=180°﹣(360°﹣∠A﹣∠D﹣∠ABC)=∠A+∠D+∠ABC﹣180°,
由三角形的外角性质得,∠DCE=∠A+∠D+∠ABC,∠OCE=∠O+∠OBC,
∵BO、CO分别是∠ABC和∠DCE的平分线,
∴∠OBC=∠ABC,∠OCE=∠DCE,
∴∠BOC+∠OBC=(∠A+∠D+∠ABC﹣180°)=(∠A+∠D)+∠ABC﹣90°,
∴∠BOC=(∠A+∠D)﹣90°,
∵∠A=n°,∠D=m°,
∴∠BOC=(n°+m°)﹣90°;
②同①可求,∠BOC=90°﹣(n°+m°).
故答案为:55;55;(n°+m°)﹣90°;90°﹣(n°+m°).
8.解:(1)∵AM是∠EAC的平分线,BN是∠FBC的平分线,
∴∠MAC+∠NCB=∠EAC+∠FBC=β,
∵AM∥BN,
∴∠C=∠MAC+∠NCB,
即α=β;
(2)∵∠EAC的平分线与∠FBC平分线相交于P,
∴∠PAC+∠PBC=∠EAC+∠FBC=β,
若点P在点C的下方,则∠C=∠APB+(∠PAC+∠PBC),
即α=∠APB+β,
若点P在点C的上方,则∠C+∠APB=∠PAC+∠PBC,
即α+∠APB=β;
综上所述,α=∠APB+β或α+∠APB=β;
(3)由(2)得,∠P1=∠C﹣(∠PAC+∠PBC)=α﹣β,
∠P2=∠P1﹣(∠P2AP1+∠P2BP1),
=α﹣β﹣β=α﹣β,
∠P3=α﹣β﹣β=α﹣β,
∠P4=α﹣β﹣β=α﹣β,
∠P5=α﹣β﹣β=α﹣β.
故答案为:(2)α=∠APB+β或α+∠APB=β;(3)α﹣β.
9.证明:∵∠1=∠2
∴AC∥DE(同位角相等,两直线平行)
∴∠3=∠5(两直线平行,内错角相等)
又∵∠3=∠4
∴∠5=∠4(等量代换)
∴BC∥EF(内错角相等,两直线平行)
故答案为:AC,DE,同位角相等,两直线平行,∠3,两直线平行,内错角相等,∠4,等量代换,内错角相等,两直线平行.
10.【定理证明】
证明:方法一:过点A作直线MN∥BC,如图所示,
∴∠MAB=∠B,∠NAC=∠C,
∵∠MAB+∠BAC+∠NAC=180°,
∴∠BAC+∠B+∠C=180°;(3分)
方法二:延长BC到点D,过点C作CE∥AB,如图所示,
∴∠A=∠ACE,∠B=∠ECD,
∵∠ACB+∠ACE+∠ECD=180°,
∴∠A+∠B+∠ACB=180°;(3分)
【定理推论】
∵∠ACD+∠ACB=180°,∠A+∠B+∠ACB=180°,
∴∠ACD=∠A+∠ABC,(4分)
故答案为:∠A+∠ABC;
【初步运用】
(1)∵∠DBC=∠A+∠ACB,
∴∠ACB=∠DBC﹣∠A=150°﹣80°=70°,
故答案为:70;(5分)
(2)∵∠A=80°,
∴∠ABC+∠ACB=100°,
∴∠DBC+∠ECB=360°﹣100°=260°,
故答案为:260;(6分)
【拓展延伸】
(1)如图④,连接AP,∵∠DBP=∠BAP+∠APB,∠ECP=∠CAP+∠APC,
∴∠DBP+∠ECP=∠BAP+∠APB+∠CAP+∠APC=∠BAC+∠BPC,
∵∠BAC=80°,∠P=150°,
∴∠DBP+∠ECP=∠BAC+∠BPC=80°+150°=230°,
故答案为:230;(7分)
(2)∠P=∠A+100°(9分)
理由是:如图⑤,设∠DBO=x,∠OCE=y,则∠DBO=∠OBP=x,∠PCO=∠OCE=y,
由(1)同理得:x+y=∠A+∠O,2x+2y=∠A+∠P,
2∠A+2∠O=∠A+∠P,
∵∠O=50°,
∴∠P=∠A+100°,
故答案为:∠P=∠A+100°;
(3)证明:延长BP交CN于点Q,
∵BM平分∠DBP,CN平分∠ECP,
∴∠DBP=2∠MBP,∠ECP=2∠NCP,
∵∠DBP+∠ECP=∠A+∠BPC,
∠A=∠BPC,
∴2∠MBP+2∠NCP=∠A+∠BPC=2∠BPC,
∴∠BPC=∠MBP+∠NCP,
∵∠BPC=∠PQC+∠NCP,
∴∠MBP=∠PQC,
∴BM∥CN(12分)
11.解:(1)在△ABC中,
∵∠BAC+∠ACB+∠ABC=180°,∠BAC=40°,∠ACB=75°,
∴∠ABC=180°﹣40°﹣75°=65°.
∵BI是∠ABC的平分线,
∴∠CBI=∠ABC=×65°=32.5°.
∵CI是∠ABC的平分线,
∴∠BCI=∠ACB=×75°=37.5°.
在△BCI
∠CBI+∠BCI+∠BIC=180°,
∴∠BIC=180°﹣32.5°﹣37.5°=110°.
(2)∵∠MBC是△ABC的外角,
∴∠MBC=∠A+∠ACB.
∵∠NCB是△ABC的外角,
∴∠NCB=∠A+∠ABC.
∴∠MBC+∠NCB=∠A+∠ACB+∠A+∠ABC=180°+∠A=180°+40°=220°.
∵BD是∠MBC的平分线,
∴∠CBD=∠MBC.
∵CD是∠NCB的平分线,
∴∠BCD=∠NCB.
∴∠CBD+∠BCD=(∠MBC+∠NCB)=×220°=110°.
在△BCD中
∠BDC+∠CBD+∠BCD=180°,
∴∠BDC=180°﹣110°=70°.
(3)∵BE是∠ABC的平分线,
∴∠CBE=∠ABC.
∵∠ACG是△ABC的外角,
∴∠ACG=∠BAC+∠ABC.
∵CE是∠ACG的平分线,
∴∠ECG=(∠BAC+∠ABC)=∠BAC+∠ABC.
∵∠ECG是△BCE的外角,
∴∠ECG=∠CBE+∠BEC.
∴∠BAC+∠ABC=∠ABC+∠BEC.
∴∠BAC=2∠BEC.
12.解:(1)由三角形内角和定理得:∠D=180°﹣(∠E+∠F)=180°﹣100°=80°,
∴∠DBC+∠DCB=180°﹣∠D=100°,
∵∠ABC+∠ACB=180°﹣∠A=144°,
∴∠ABF+∠ACE=180°﹣(∠ABC+∠DBC)+180°﹣(∠ACB+∠DCB)=360°﹣100°﹣144°=116°;
故答案为:116;
(2)∠ABF+∠ACE=316°;理由如下;在△ABC中,∠A=36°,
∴∠ABC+∠ACB=180°﹣∠A=144°,
在△DEF中,∠E+∠F=100°,
∴∠D=180°﹣100°=80°,
∴∠BCD+∠CBD=180°﹣∠D=100°,
∴∠ABD+∠ACD=(∠ABC+∠ACB)﹣(∠BCD+∠CBD)=144°﹣100°=44°,
∴∠ABF+∠ACE=180°﹣∠ABD+180°﹣∠ACD=360°﹣(∠ABD+∠ACD)=360°﹣44°=316°;
(3)不存在.假设能将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB.
则∠CBD+∠BCD=∠ABD+∠ACD=100°,
那么∠ABC+∠ACB=200°,与三角形内角和定理矛盾,
∴不存在;
如果存在,根据两内角平分线模型,可知∠D=90°+∠A,题中∠D=80°,∠A=36°,
∴只要∠E+∠F=100°改成∠E+∠F=72°.
13.解:(1)如图①,∵∠DAE=40°,∠ADE=∠AED,
∴∠ADE=70°,
∵∠BAC=100°,
∴∠BAD=∠BAC﹣∠DAE=100°﹣40°=60°,
∵∠B=∠C=40°,
∴∠ADC=∠B+∠BAD=40°+60°=100°,
∴∠CDE=30°,
∴==2,
故答案为:30°,2;
(2)如图①,∠BAD与∠CDE的数量关系是:∠BAD=2∠CDE;
理由是:设∠DAE=x,∠BAC=y,则∠BAD=y﹣x,
∵∠DAE=x,∠ADE=∠AED,
∴∠ADE=,
∵∠B=∠C=,
∴∠ADC=∠B+∠BAD=+y﹣x=90°+y﹣x,
∴∠CDE=∠ADC﹣∠ADE=90°+y﹣x﹣=,
∴∠BAD=2∠CDE;
(3)如图②,∠BAD与∠CDE的数量关系:∠BAD=2∠CDE,
理由是:设∠DAE=x,∠BAC=y,则∠BAD=x+y,
∵∠DAE=x,∠ADE=∠AED,
∴∠ADE=∠E=,
∵∠B=,
∴∠ACD=∠B+∠BAC=∠E+∠CDE,
∴+y=+∠CDE,
∴∠CDE=(x+y),
∴∠BAD=2∠CDE;
故答案为:∠BAD=2∠CDE;
(4)分两种情况:
①当E在射线CA上时,如图③,
设∠DAE=x,∠BAC=y,则x+y=180°﹣26°=154°,
∵∠DAE=x,∠ADE=∠AED,
∴∠AED=,
∵∠C=,
△CDE中,∠CDE=180°﹣∠AED﹣∠C=180°﹣﹣=(x+y)==77°
②当E在射线AC上时,如图④,
设∠DAE=x,∠BAC=y,则x﹣y=26°,
∵∠DAE=x,∠ADE=∠AED,
∴∠AED=,
∵∠ACB=,
△CDE中,∠CDE=∠ACB﹣∠AED=﹣=(x﹣y)==13°,
综上,∠CDE=13°或77°;
故答案为:13或77.
14.解:∵∠ABC=∠ADC,
∴∠ABC=∠ADC
又∵BF、DE分别平分∠ABC与∠ADC,
∴∠1=ABC,∠2=∠ADC
∵∠1=∠2.
∵∠1=∠3,(已知)
∴∠2=3.(等量代换)
∴AB∥CD.(内错角相等,两直线平行).
15.解:(1)∵CE平分∠ACD,
∴∠ACE=∠DCE,
∵∠DCE=∠B+∠E,
∴∠ACE=∠B+∠E,
∵∠BAC=∠ACE+∠E,
∴∠BAC=∠B+∠E+∠E=∠B+2∠E.
(2)设∠CAF=α,则∠ACE=∠DCE=2α,
∵AF⊥BC,
∴∠AFC=90°,
∴∠ACF=90°﹣α,
∵∠ACF+∠ACE+∠DCE=180°,
∴90°﹣α+2α+2α=180°,
解得:α=30°,
∴∠ACE=60°=∠B+∠E,
又∵∠B=2∠E,
∴∠B=40°、∠E=20°,
∴∠BAC=∠B+2∠E=80°.
第七章
平面的图形认识(二)
解答题专项提升(一)
1.如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F.
(1)∠ABC=40°,∠A=60°,求∠BFD的度数;
(2)直接写出∠A与∠BFD的数量关系.
2.如图1,在四边形ABCD中,∠ABC+∠ADC=180°,BE、DF分别是∠ABC与∠ADC的平分线,∠ADF与∠AFD互余.
(1)试判断直线BE与DF的位置关系,并说明理由;
(2)如图2,延长CB、DF相交于点G,过点B作BH⊥FG,垂足为点H,试判断∠FBH与∠GBH的大小关系,并说明理由.
3.如图所示,AD⊥BC于点D,EG⊥BC于点G,若∠E=∠1,则∠2=∠3吗?
下面是推理过程,请你填空或填写理由.
证明:∵AD⊥BC于点D,EG⊥BC于点G(已知),
∴∠ADC=∠EGC=90°
,
∴AD∥EG(
),
∴∠1=∠2(
),
∵∠E=∠1(已知)
∴∠E=∠2(等量代换)
∵AD∥EG,
∴
=∠3(两直线平行,同位角相等).
∴
=
(等量代换)
4.如图,已知:AD⊥BC于D,EG⊥BC于G,∠E=∠1.求证:AD平分∠BAC.
5.如图①,已知直线l1、l2,直线l3和直线l1、l2交于点C和D,在直线l3上有动点P(点P与点C、D不重合),点A在直线l1上,点B在直线l2上.
(1)问题发现:如果点P在C、D之间运动时,且满足∠1+∠3=∠2,请写出l1与l2之间的位置关系
;(2)拓展探究:如图②如果l1∥l2,点P在直线l1的上方运动时,试猜想∠1+∠2与∠3之间关系并给予证明;
(3)问题解决:如果l1∥l2,点P在直线l2的下方运动时,请直接写出∠PAC、∠PBD、∠APB之间的关系.
6.如图,∠1=∠2,∠BAE=∠BDE,EA平分∠BEF.
(1)求证:AB∥DE;
(2)BD平分∠EBC吗?为什么?
7.在△ABC中,∠A=70°.
(1)如图①∠ABC,∠ACB
的平分线相交于点O,则∠BOC=
°;
(2)如图②△ABC的外角∠CBD,∠BCE
的平分线相交于点O',则∠BO'C=
°;
(3)探究
探究一:如图③,△ABC的内角∠ABC的平分线与其外角∠ACD
的平分线相交于点O,设∠A=n°,求∠BOC的度数.(用n的代数式表示)
探究二:已知:四边形ABCD的内角∠ABC的平分线所在直线与其外角∠DCE的平分线所在直线
相交于点O,∠A=n°,∠D=m°
①如图④,若∠A+∠D≥180°,则∠BOC=
(用m、n的代数式表示)
②如图⑤,若∠A+∠D<180°,则∠BOC=
(用m、n的代数式表示)
8.若∠C=α,∠EAC+∠FBC=β
(1)如图①,AM是∠EAC的平分线,BN是∠FBC的平分线,若AM∥BN,则α与β有何关系?并说明理由.
(2)如图②,若∠EAC的平分线所在直线与∠FBC平分线所在直线交于P,试探究∠APB与α、β的关系是
.(用α、β表示)
(3)如图③,若α≥β,∠EAC与∠FBC的平分线相交于P1,∠EAP1与∠FBP1的平分线交于P2;依此类推,则∠P5=
.(用α、β表示)
9.推理填空:
已知,如图∠1=∠2,∠3=∠4,求证:BC∥EF.
证明:∵∠1=∠2
∴
∥
(
)
∴
=∠5
(
)
又∵∠3=∠4
∴∠5=
(
)
∴BC∥EF
(
)
10.三角形内角和定理告诉我们:三角形三个内角的和等于180°.如何证明这个定理呢?
我们知道,平角是180°,要证明这个定理就是把三角形的三个内角转移到一个平角中去,请根据如下条件,证明定理.
【定理证明】
已知:△ABC(如图①).
求证:∠A+∠B+∠C=180°.
【定理推论】如图②,在△ABC中,有∠A+∠B+∠ACB=180°,点D是BC延长线上一点,由平角的定义可得∠ACD+∠ACB=180°,所以∠ACD=
.从而得到三角形内角和定理的推论:三角形的外角等于与它不相邻的两个内角的和.
【初步运用】如图③,点D、E分别是△ABC的边AB、AC延长线上一点.
(1)若∠A=80°,∠DBC=150°,则∠ACB=
°;
(2)若∠A=80°,则∠DBC+∠ECB=
°.
【拓展延伸】如图④,点D、E分别是四边形ABPC的边AB、AC延长线上一点.
(1)若∠A=80°,∠P=150°,则∠DBP+∠ECP=
°;
(2)分别作∠DBP和∠ECP的平分线,交于点O,如图⑤,若∠O=50°,则∠A和∠P的数量关系为
;
(3)分别作∠DBP和∠ECP的平分线BM、CN,如图⑥,若∠A=∠P,求证:BM∥CN.
11.如图,在△ABC中,∠BAC=40°,∠ACB=75°,点I是两条角平分线的交点.
(1)求∠BIC的度数;
(2)若点D是两条外角平分线的交点,求∠BDC的度数;
(3)若点E是内角∠ABC、外角∠ACG的平分线交点,试探索∠BEC与∠BAC的数量关系,并说明理由.
12.已知:在△ABC和△DEF中,∠A=36°,∠E+∠F=100°,将△DEF如图放置,使得∠D的两条边分别经过点B和点C.
(1)当将△DEF如图1摆放时,∠ABF+∠ACE=
°.
(2)当将△DEF如图2摆放时,试问:∠ABF+∠ACE等于多少度?请说明理由.
(3)如图2,是否存在将△DEF摆放到某个位置时,使得BD,CD分别平分∠ABC和∠ACB?如果存在,请画出图形或说明理由.如果不存在,请改变题目中的一个已知条件,使之存在.
13.如图①,在△ABC中,∠B=∠C,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连接DE.
(1)若∠BAC=100°,∠DAE=40°,则∠CDE=
,此时=
;
(2)若点D在BC边上(点B、C除外)运动,试探究∠BAD与∠CDE的数量关系并说明理由;
(3)若点D在线段BC的延长线上,点E在线段AC的延长线上(如图②),其余条件不变,请直接写出∠BAD与∠CDE的数量关系:
;
(4)若点D在线段CB的延长线上(如图③)、点E在直线AC上,∠BAD=26°,其余条件不变,则∠CDE=
°(友情提醒:可利用图③画图分析)
14.已知:如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC,且∠1=∠3.说明AB∥DC的理由.
解:∵∠ABC=∠ADC,
∴∠ABC=∠ADC
又∵BF、DE分别平分∠ABC与∠ADC,
∴∠1=ABC,∠2=∠ADC
∴∠
=∠
.(等量代换)
∵∠1=∠3,
∴∠2=
.
∴
∥
.
.
15.已知:CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
(1)如图1,求证∠BAC=∠B+2∠E;
(2)如图2,过点A作AF⊥BC,垂足为点F,若∠DCE=2∠CAF,∠B=2∠E,求∠BAC的度数.
参考答案
1.解:(1)∵∠ABC=40°,∠A=60°,
∴∠ACB=180°﹣40°﹣60°=80°,
∵∠B、∠C的平分线BE,CD相交于点F,
∴∠BFD=∠FBC+∠FCB=∠ABC+∠ACB=20°+40°=60°.
(2)∵∠B、∠C的平分线BE,CD相交于点F,
∴∠BFD=∠FBC+∠FCB=∠ABC+∠ACB=(∠ABC+∠ACB)=(180°﹣∠A)=90°﹣∠A.
2.解:(1)BE∥DF,
理由:∵BE、DF分别是∠ABC与∠ADC的平分线,
∴∠ABE=∠CBE=∠ABC,∠ADF=∠CDF=∠ADC,
∵∠ABC+∠ADC=180°,
∴∠ABE+∠ADF=90°,
∵∠ADF与∠AFD互余,
∴∠ADF+∠AFD=90°,
∴∠ABE=∠AFD,
∴BE∥DF;
(2)∠FBH=∠GBH,
理由:由(1)知BE∥DF,
∴BE∥DG,
∴∠EBH+∠DHB=180°,
∵BH⊥FG,
∴∠DHB=90°,
∴∠EBH=180°﹣∠DHB=90°.
∴∠CBE+∠GBH=180°﹣∠EBH=90°,
∵∠ABE+∠ABH=∠EBH=90°,
∵∠ABE=∠CBE,
∴∠ABH=∠GBH,
即∠FBH=∠GBH.
3.证明:∵AD⊥BC于点D,EG⊥BC于点G(已知),
∴∠ADC=∠EGC=90°(垂直的定义),
∴AD∥EG(同位角相等,两直线平行),
∴∠1=∠2(两直线平行,内错角相等),
∵∠E=∠1(已知)
∴∠E=∠2(等量代换)
∵AD∥EG,
∴∠E=∠3(两直线平行,同位角相等).
∴∠2=∠3(等量代换),
故答案为:垂直的定义,同位角相等,两直线平行,两直线平行,同位角相等,∠E,∠2,∠3.
4.证明:∵AD⊥BC于D,EG⊥BC于G,(已知)
∴∠ADC=∠EGC=90°,
∴AD∥EG,(同位角相等,两直线平行).
∴∠1=∠2,(两直线平行,内错角相等).
∠E=∠3(两直线平行,同位角相等)
又∵∠E=∠1(已知)
∴∠2=∠3,(等量代换).
∴AD平分∠BAC.(角平分线的定义)
5.证明:(1)如图①,延长BP交AC于E,
∵∠2=∠1+∠3,∠2=∠1+∠AEP,
∴∠3=∠AEP,
∴l1∥l2,
故答案为:l1∥l2;
(2)如图②所示,当点P在线段DC的延长线上时,∠1+∠2=∠3,
理由是:∵l1∥l2,
∴∠CEP=∠3
∵∠CEP=∠1+∠2,
∴∠1+∠2=∠3;
(3)如图③所示,当点P在直线l2的下方运动时,∠APB+∠PBD=∠PAC.
理由:过点P作PF∥l1,
∠FPA=∠1.
∵l1∥l2,
∴PF∥l2,
∴∠FPB=∠3,
∴∠FPA=∠2+∠FPB=∠2+∠3;
即∠APB+∠PBD=∠PAC.
6.(1)证明:∵∠2与∠ABE是对顶角,
∴∠2=∠ABE.
∵∠1=∠2,
∴∠1=∠ABE,
∴AB∥DE;
(2)解:BD平分∠EBC.
理由:∵由(1)知AB∥CD,
∴∠AED+∠BAE=180°,∠BEF=∠EBC.
∵∠BAE=∠BDE,
∴∠AED+∠BDE=180°,
∴AE∥BD,
∴∠AEB=∠DBE.
∵EA平分∠BEF,∠BEF=∠EBC,
∴BD平分∠EBC.
7.解:(1)∵∠A=70°,
∴∠ABC+∠ACB=180°﹣∠A=110°,
∵BO、CO分别是∠ABC和∠ACB的平分线,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=×110°=55°,
∴在△BOC中,∠BOC=180°﹣(∠OBC+∠OCB)=125°;
(2)∵∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC,
∴∠DBC+∠ECB=∠A+∠ACB+∠A+∠ABC=180°+∠A,
∵BO、CO分别是△ABC两个外角∠CBD和∠BCE的平分线,
∴∠OBC=∠DBC,∠OCB=∠ECB,
∴∠OBC+∠OCB=(180°+∠A),
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(180°+∠A)=90°﹣∠A=55°;
(3)探究
探究一:∵BO和CO分别是∠ABC和∠ACD的角平分线,
∴∠OBC=∠ABC,∠OCE=∠ACD,
又∵∠ACD是△ABC的一外角,
∴∠ACD=∠A+∠ABC,
∴∠OCE=(∠A+∠ABC)=∠A+∠OBC,
∵∠OCE是△BOC的一外角,
∴∠BOC=∠OCE﹣∠OBC=∠A+∠OBC﹣∠OBC=∠A=n°;
探究二:①由四边形内角和定理得,∠BCD=360°﹣∠A﹣∠D﹣∠ABC,
∴∠DCE=180°﹣(360°﹣∠A﹣∠D﹣∠ABC)=∠A+∠D+∠ABC﹣180°,
由三角形的外角性质得,∠DCE=∠A+∠D+∠ABC,∠OCE=∠O+∠OBC,
∵BO、CO分别是∠ABC和∠DCE的平分线,
∴∠OBC=∠ABC,∠OCE=∠DCE,
∴∠BOC+∠OBC=(∠A+∠D+∠ABC﹣180°)=(∠A+∠D)+∠ABC﹣90°,
∴∠BOC=(∠A+∠D)﹣90°,
∵∠A=n°,∠D=m°,
∴∠BOC=(n°+m°)﹣90°;
②同①可求,∠BOC=90°﹣(n°+m°).
故答案为:55;55;(n°+m°)﹣90°;90°﹣(n°+m°).
8.解:(1)∵AM是∠EAC的平分线,BN是∠FBC的平分线,
∴∠MAC+∠NCB=∠EAC+∠FBC=β,
∵AM∥BN,
∴∠C=∠MAC+∠NCB,
即α=β;
(2)∵∠EAC的平分线与∠FBC平分线相交于P,
∴∠PAC+∠PBC=∠EAC+∠FBC=β,
若点P在点C的下方,则∠C=∠APB+(∠PAC+∠PBC),
即α=∠APB+β,
若点P在点C的上方,则∠C+∠APB=∠PAC+∠PBC,
即α+∠APB=β;
综上所述,α=∠APB+β或α+∠APB=β;
(3)由(2)得,∠P1=∠C﹣(∠PAC+∠PBC)=α﹣β,
∠P2=∠P1﹣(∠P2AP1+∠P2BP1),
=α﹣β﹣β=α﹣β,
∠P3=α﹣β﹣β=α﹣β,
∠P4=α﹣β﹣β=α﹣β,
∠P5=α﹣β﹣β=α﹣β.
故答案为:(2)α=∠APB+β或α+∠APB=β;(3)α﹣β.
9.证明:∵∠1=∠2
∴AC∥DE(同位角相等,两直线平行)
∴∠3=∠5(两直线平行,内错角相等)
又∵∠3=∠4
∴∠5=∠4(等量代换)
∴BC∥EF(内错角相等,两直线平行)
故答案为:AC,DE,同位角相等,两直线平行,∠3,两直线平行,内错角相等,∠4,等量代换,内错角相等,两直线平行.
10.【定理证明】
证明:方法一:过点A作直线MN∥BC,如图所示,
∴∠MAB=∠B,∠NAC=∠C,
∵∠MAB+∠BAC+∠NAC=180°,
∴∠BAC+∠B+∠C=180°;(3分)
方法二:延长BC到点D,过点C作CE∥AB,如图所示,
∴∠A=∠ACE,∠B=∠ECD,
∵∠ACB+∠ACE+∠ECD=180°,
∴∠A+∠B+∠ACB=180°;(3分)
【定理推论】
∵∠ACD+∠ACB=180°,∠A+∠B+∠ACB=180°,
∴∠ACD=∠A+∠ABC,(4分)
故答案为:∠A+∠ABC;
【初步运用】
(1)∵∠DBC=∠A+∠ACB,
∴∠ACB=∠DBC﹣∠A=150°﹣80°=70°,
故答案为:70;(5分)
(2)∵∠A=80°,
∴∠ABC+∠ACB=100°,
∴∠DBC+∠ECB=360°﹣100°=260°,
故答案为:260;(6分)
【拓展延伸】
(1)如图④,连接AP,∵∠DBP=∠BAP+∠APB,∠ECP=∠CAP+∠APC,
∴∠DBP+∠ECP=∠BAP+∠APB+∠CAP+∠APC=∠BAC+∠BPC,
∵∠BAC=80°,∠P=150°,
∴∠DBP+∠ECP=∠BAC+∠BPC=80°+150°=230°,
故答案为:230;(7分)
(2)∠P=∠A+100°(9分)
理由是:如图⑤,设∠DBO=x,∠OCE=y,则∠DBO=∠OBP=x,∠PCO=∠OCE=y,
由(1)同理得:x+y=∠A+∠O,2x+2y=∠A+∠P,
2∠A+2∠O=∠A+∠P,
∵∠O=50°,
∴∠P=∠A+100°,
故答案为:∠P=∠A+100°;
(3)证明:延长BP交CN于点Q,
∵BM平分∠DBP,CN平分∠ECP,
∴∠DBP=2∠MBP,∠ECP=2∠NCP,
∵∠DBP+∠ECP=∠A+∠BPC,
∠A=∠BPC,
∴2∠MBP+2∠NCP=∠A+∠BPC=2∠BPC,
∴∠BPC=∠MBP+∠NCP,
∵∠BPC=∠PQC+∠NCP,
∴∠MBP=∠PQC,
∴BM∥CN(12分)
11.解:(1)在△ABC中,
∵∠BAC+∠ACB+∠ABC=180°,∠BAC=40°,∠ACB=75°,
∴∠ABC=180°﹣40°﹣75°=65°.
∵BI是∠ABC的平分线,
∴∠CBI=∠ABC=×65°=32.5°.
∵CI是∠ABC的平分线,
∴∠BCI=∠ACB=×75°=37.5°.
在△BCI
∠CBI+∠BCI+∠BIC=180°,
∴∠BIC=180°﹣32.5°﹣37.5°=110°.
(2)∵∠MBC是△ABC的外角,
∴∠MBC=∠A+∠ACB.
∵∠NCB是△ABC的外角,
∴∠NCB=∠A+∠ABC.
∴∠MBC+∠NCB=∠A+∠ACB+∠A+∠ABC=180°+∠A=180°+40°=220°.
∵BD是∠MBC的平分线,
∴∠CBD=∠MBC.
∵CD是∠NCB的平分线,
∴∠BCD=∠NCB.
∴∠CBD+∠BCD=(∠MBC+∠NCB)=×220°=110°.
在△BCD中
∠BDC+∠CBD+∠BCD=180°,
∴∠BDC=180°﹣110°=70°.
(3)∵BE是∠ABC的平分线,
∴∠CBE=∠ABC.
∵∠ACG是△ABC的外角,
∴∠ACG=∠BAC+∠ABC.
∵CE是∠ACG的平分线,
∴∠ECG=(∠BAC+∠ABC)=∠BAC+∠ABC.
∵∠ECG是△BCE的外角,
∴∠ECG=∠CBE+∠BEC.
∴∠BAC+∠ABC=∠ABC+∠BEC.
∴∠BAC=2∠BEC.
12.解:(1)由三角形内角和定理得:∠D=180°﹣(∠E+∠F)=180°﹣100°=80°,
∴∠DBC+∠DCB=180°﹣∠D=100°,
∵∠ABC+∠ACB=180°﹣∠A=144°,
∴∠ABF+∠ACE=180°﹣(∠ABC+∠DBC)+180°﹣(∠ACB+∠DCB)=360°﹣100°﹣144°=116°;
故答案为:116;
(2)∠ABF+∠ACE=316°;理由如下;在△ABC中,∠A=36°,
∴∠ABC+∠ACB=180°﹣∠A=144°,
在△DEF中,∠E+∠F=100°,
∴∠D=180°﹣100°=80°,
∴∠BCD+∠CBD=180°﹣∠D=100°,
∴∠ABD+∠ACD=(∠ABC+∠ACB)﹣(∠BCD+∠CBD)=144°﹣100°=44°,
∴∠ABF+∠ACE=180°﹣∠ABD+180°﹣∠ACD=360°﹣(∠ABD+∠ACD)=360°﹣44°=316°;
(3)不存在.假设能将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB.
则∠CBD+∠BCD=∠ABD+∠ACD=100°,
那么∠ABC+∠ACB=200°,与三角形内角和定理矛盾,
∴不存在;
如果存在,根据两内角平分线模型,可知∠D=90°+∠A,题中∠D=80°,∠A=36°,
∴只要∠E+∠F=100°改成∠E+∠F=72°.
13.解:(1)如图①,∵∠DAE=40°,∠ADE=∠AED,
∴∠ADE=70°,
∵∠BAC=100°,
∴∠BAD=∠BAC﹣∠DAE=100°﹣40°=60°,
∵∠B=∠C=40°,
∴∠ADC=∠B+∠BAD=40°+60°=100°,
∴∠CDE=30°,
∴==2,
故答案为:30°,2;
(2)如图①,∠BAD与∠CDE的数量关系是:∠BAD=2∠CDE;
理由是:设∠DAE=x,∠BAC=y,则∠BAD=y﹣x,
∵∠DAE=x,∠ADE=∠AED,
∴∠ADE=,
∵∠B=∠C=,
∴∠ADC=∠B+∠BAD=+y﹣x=90°+y﹣x,
∴∠CDE=∠ADC﹣∠ADE=90°+y﹣x﹣=,
∴∠BAD=2∠CDE;
(3)如图②,∠BAD与∠CDE的数量关系:∠BAD=2∠CDE,
理由是:设∠DAE=x,∠BAC=y,则∠BAD=x+y,
∵∠DAE=x,∠ADE=∠AED,
∴∠ADE=∠E=,
∵∠B=,
∴∠ACD=∠B+∠BAC=∠E+∠CDE,
∴+y=+∠CDE,
∴∠CDE=(x+y),
∴∠BAD=2∠CDE;
故答案为:∠BAD=2∠CDE;
(4)分两种情况:
①当E在射线CA上时,如图③,
设∠DAE=x,∠BAC=y,则x+y=180°﹣26°=154°,
∵∠DAE=x,∠ADE=∠AED,
∴∠AED=,
∵∠C=,
△CDE中,∠CDE=180°﹣∠AED﹣∠C=180°﹣﹣=(x+y)==77°
②当E在射线AC上时,如图④,
设∠DAE=x,∠BAC=y,则x﹣y=26°,
∵∠DAE=x,∠ADE=∠AED,
∴∠AED=,
∵∠ACB=,
△CDE中,∠CDE=∠ACB﹣∠AED=﹣=(x﹣y)==13°,
综上,∠CDE=13°或77°;
故答案为:13或77.
14.解:∵∠ABC=∠ADC,
∴∠ABC=∠ADC
又∵BF、DE分别平分∠ABC与∠ADC,
∴∠1=ABC,∠2=∠ADC
∵∠1=∠2.
∵∠1=∠3,(已知)
∴∠2=3.(等量代换)
∴AB∥CD.(内错角相等,两直线平行).
15.解:(1)∵CE平分∠ACD,
∴∠ACE=∠DCE,
∵∠DCE=∠B+∠E,
∴∠ACE=∠B+∠E,
∵∠BAC=∠ACE+∠E,
∴∠BAC=∠B+∠E+∠E=∠B+2∠E.
(2)设∠CAF=α,则∠ACE=∠DCE=2α,
∵AF⊥BC,
∴∠AFC=90°,
∴∠ACF=90°﹣α,
∵∠ACF+∠ACE+∠DCE=180°,
∴90°﹣α+2α+2α=180°,
解得:α=30°,
∴∠ACE=60°=∠B+∠E,
又∵∠B=2∠E,
∴∠B=40°、∠E=20°,
∴∠BAC=∠B+2∠E=80°.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
