2020-2021学年人教版数学七年级下册第6章 实数-单元复习课件(共21张ppt)
文档属性
| 名称 | 2020-2021学年人教版数学七年级下册第6章 实数-单元复习课件(共21张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 772.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 15:19:54 | ||
图片预览


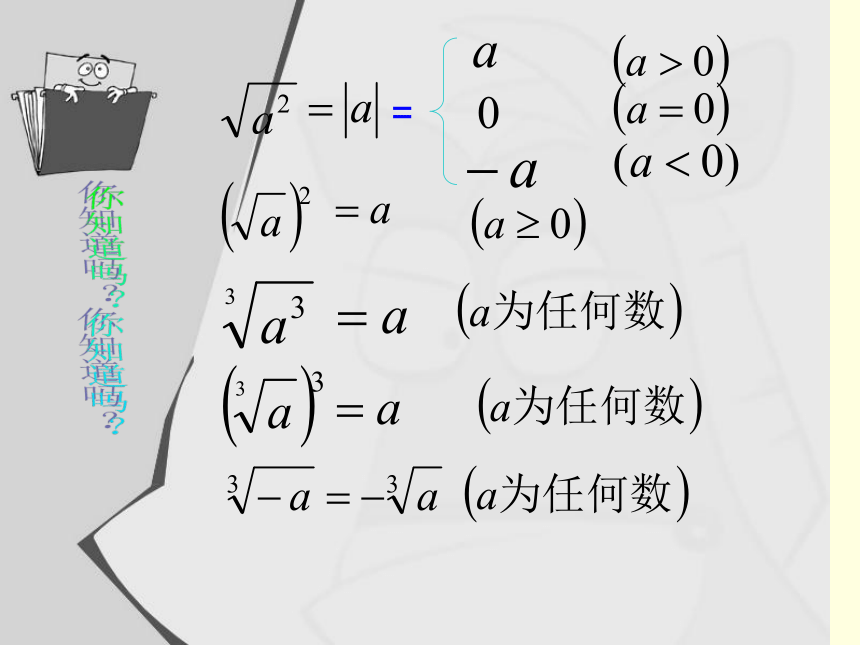
文档简介
(共21张PPT)
第六章
实
数
学习目标:
(1)梳理本章的相关概念,通过回顾平方根、立方根、实数及有关的概念,强化概念之间的联系.
(2)会进行开平方和开立方运算.
学习重点:
(1)进一步加强学生对平方根、立方根以及实数概念的认识.
(2)进一步强化平方根、立方根的联系,有理数与实数运算的联系.
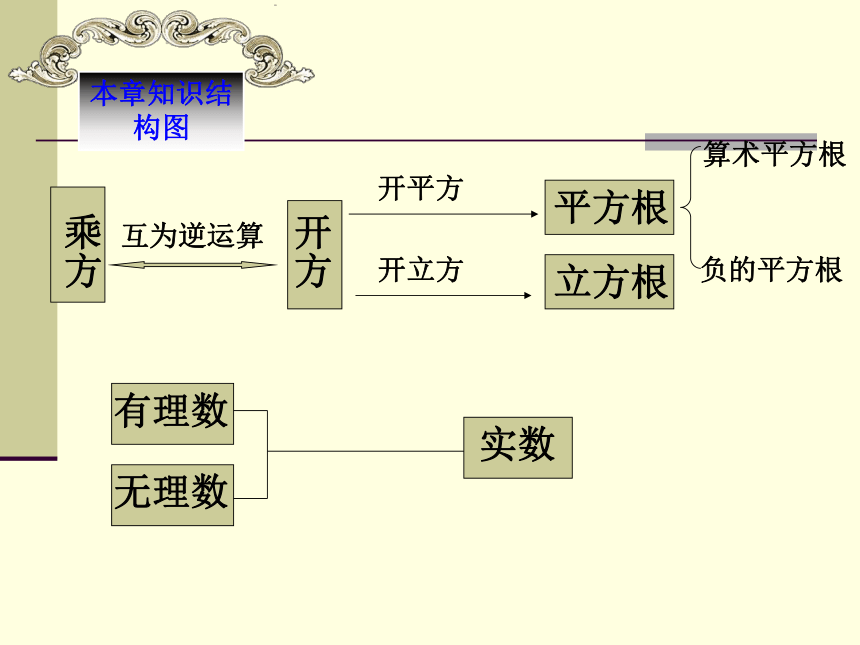
本章知识结构图
乘方
开方
开平方
开立方
平方根
立方根
有理数
无理数
实数
互为逆运算
算术平方根
负的平方根
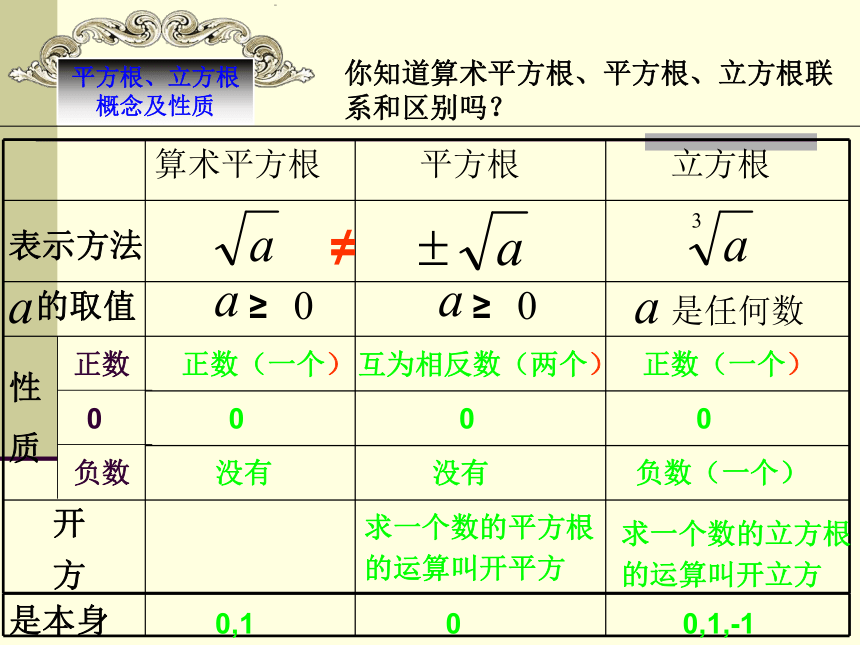
平方根、立方根概念及性质
你知道算术平方根、平方根、立方根联系和区别吗?
算术平方根
平方根
立方根
表示方法
的取值
性
质
≥
开
方
≥
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
≠
是本身
0,1
0
0,1,-1
=
你知道吗?
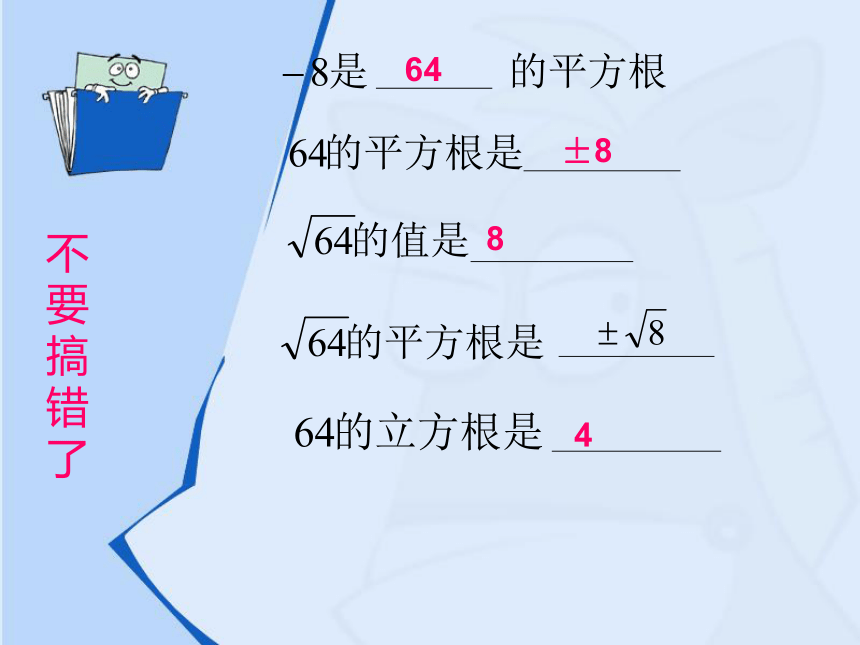
不要搞错了
64
±8
8
4
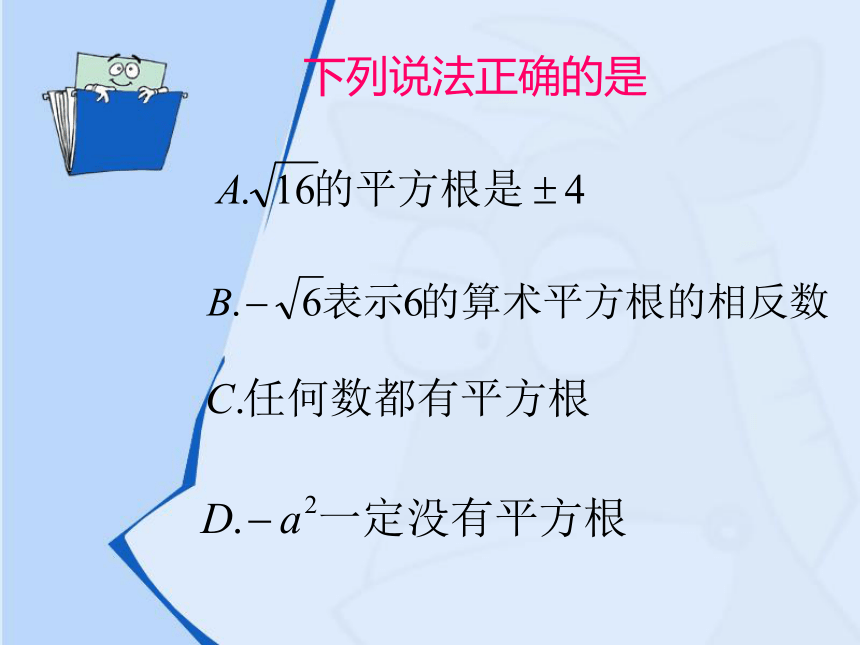
下列说法正确的是
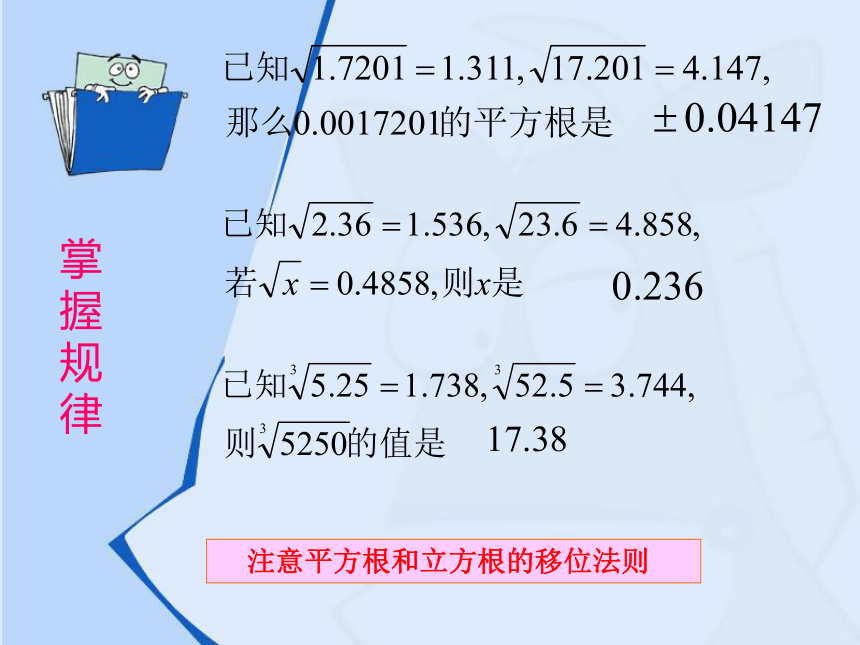
掌握规律
注意平方根和立方根的移位法则
实数
有理数
无理数
正整数
0
负整数
正分数
负分数
分数
整数
自然数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
一般有三种情况
1.圆周率
及一些含有
的数
2.开不尽方的数
3.有一定的规律,但不循环的无限小数
把下列各数分别填入相应的集合内:
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
你能区分开吗?
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
(1)a是一个实数,它的相反数为
,
绝对值为
;
(2)如果a
0,那么它的倒数为
.
是负数
等于它的相反数
是正数
等于它本身
是负数
里面的数的符号
化简绝对值要看它
等于它的相反数
例1、比较大小:
与
例2、已知实数a、b在数轴上对应点的位置如图1-2;
化简:
解:∵(-2+
)-(-2+
)=-2+
+2-
=
-
>0
∴-2+
>-2+
另解:直接由正负决定-2+
>-2+
解:由图知:b<a<0,∴a-b>0,a+b<0.
∴|a-b|+
=(a-b)+|a+b|
=a-b+[-(a+b)]
=a-b-a-b
=-2b.
b
a
o
x
实数的大小比较方法多种,要具体观察实数的特点,灵活选择最好的比较方法
比较大小的方法
适用范围
主要的依据
举例
利用数轴比较
所有实数
实数与数轴上的点是一一对应关系,有大小顺序排列。
(略)
利用绝对值比较
负实数
两负实数比较,绝对值大的反而小,绝对值小的反而大。
-√5、-3
求平方比较
正实数
两正数比较,平方值大的数大,平方值小的数小。
课本p79练习/3;课本p87练习/6(1)
求差比较
同号实数
对于同号实数a、b,
若a-b≧0,则a
≧b
(略)
求商比较
同号正实数
对于同号正实数a、b,
若a∕b≧1,则a
≧b
(略)
计算近似值比较
含无理数的实数
牢牢记住
的近似值,直接计算比较
课本p72练习/2(2);课本p87练习/6
1.求下列各数的平方根:
2.x取何值时,下列各式有意义
自我检查
3、
4、已知
求x+y的值
1.当x
时,2x-1没有平方根
2.若
,则x的值是
3.一个正数x的两个平方根分别是a+1和a-3,则
a=
,
x=
X=7
4
1
≥0.5
提高训练
已知:
,求
的算术平方根
已知:
满足
,
求
的平方根
小结与反思:
本节课你学到了什么?
有什么收获?
小组交流。
课堂小卷
一、填一填:
1.16的平方根记作_______,等于________.
2.
的值为________.
3.计算
+
=________.
4.-
的倒数是_______.
5.两个无理数的和为有理数,这两个无理数可以是______和_______.
6.若│x2-25│+
=0,则x=_______,y=_______.
7.已知x的平方根是±8,则x的立方根是________.
二、选一选:
8.4的平方根是(
)
A.2
B.-2
C.±2
D.±9.下列各式中,无意义的是(
)
A.-
B.
C.
D.
10.下列各组数中,互为相反数的一组是(
)
A.-2与
B.-2与
C.-2与-
D.│-2│与2
11.
下列说法正确的是
(
)
A.1的平方根是1;
B.1的算术平方根是1;
C.-2是2的平方根;
D.-1的平方根是-1
三、做一做:
12.
求下列各数的平方根:
(1)81;(2);(3)1.44;(4)2;
(5).
13.
求下列各式中的x:
①x2=1.21;
②27(x+1)3+64=0.
14.
a≥0时,才有意义——表示a的算术平方根.由此你会求下列各式有意义时x的取值范围吗?试试看:
(1)
(2)
(3)
(4)
+
15.已知2a-1的平方根是±3,3a+b-1的平方根是±4,求a+2b的平方根.
第六章
实
数
学习目标:
(1)梳理本章的相关概念,通过回顾平方根、立方根、实数及有关的概念,强化概念之间的联系.
(2)会进行开平方和开立方运算.
学习重点:
(1)进一步加强学生对平方根、立方根以及实数概念的认识.
(2)进一步强化平方根、立方根的联系,有理数与实数运算的联系.
本章知识结构图
乘方
开方
开平方
开立方
平方根
立方根
有理数
无理数
实数
互为逆运算
算术平方根
负的平方根
平方根、立方根概念及性质
你知道算术平方根、平方根、立方根联系和区别吗?
算术平方根
平方根
立方根
表示方法
的取值
性
质
≥
开
方
≥
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
≠
是本身
0,1
0
0,1,-1
=
你知道吗?
不要搞错了
64
±8
8
4
下列说法正确的是
掌握规律
注意平方根和立方根的移位法则
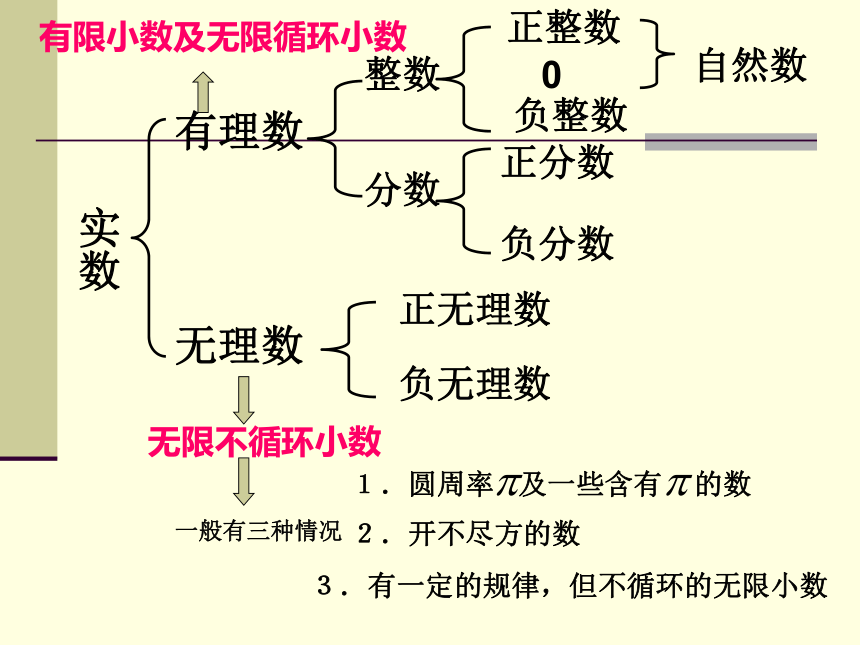
实数
有理数
无理数
正整数
0
负整数
正分数
负分数
分数
整数
自然数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
一般有三种情况
1.圆周率
及一些含有
的数
2.开不尽方的数
3.有一定的规律,但不循环的无限小数
把下列各数分别填入相应的集合内:
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
你能区分开吗?
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
(1)a是一个实数,它的相反数为
,
绝对值为
;
(2)如果a
0,那么它的倒数为
.
是负数
等于它的相反数
是正数
等于它本身
是负数
里面的数的符号
化简绝对值要看它
等于它的相反数
例1、比较大小:
与
例2、已知实数a、b在数轴上对应点的位置如图1-2;
化简:
解:∵(-2+
)-(-2+
)=-2+
+2-
=
-
>0
∴-2+
>-2+
另解:直接由正负决定-2+
>-2+
解:由图知:b<a<0,∴a-b>0,a+b<0.
∴|a-b|+
=(a-b)+|a+b|
=a-b+[-(a+b)]
=a-b-a-b
=-2b.
b
a
o
x
实数的大小比较方法多种,要具体观察实数的特点,灵活选择最好的比较方法
比较大小的方法
适用范围
主要的依据
举例
利用数轴比较
所有实数
实数与数轴上的点是一一对应关系,有大小顺序排列。
(略)
利用绝对值比较
负实数
两负实数比较,绝对值大的反而小,绝对值小的反而大。
-√5、-3
求平方比较
正实数
两正数比较,平方值大的数大,平方值小的数小。
课本p79练习/3;课本p87练习/6(1)
求差比较
同号实数
对于同号实数a、b,
若a-b≧0,则a
≧b
(略)
求商比较
同号正实数
对于同号正实数a、b,
若a∕b≧1,则a
≧b
(略)
计算近似值比较
含无理数的实数
牢牢记住
的近似值,直接计算比较
课本p72练习/2(2);课本p87练习/6
1.求下列各数的平方根:
2.x取何值时,下列各式有意义
自我检查
3、
4、已知
求x+y的值
1.当x
时,2x-1没有平方根
2.若
,则x的值是
3.一个正数x的两个平方根分别是a+1和a-3,则
a=
,
x=
X=7
4
1
≥0.5
提高训练
已知:
,求
的算术平方根
已知:
满足
,
求
的平方根
小结与反思:
本节课你学到了什么?
有什么收获?
小组交流。
课堂小卷
一、填一填:
1.16的平方根记作_______,等于________.
2.
的值为________.
3.计算
+
=________.
4.-
的倒数是_______.
5.两个无理数的和为有理数,这两个无理数可以是______和_______.
6.若│x2-25│+
=0,则x=_______,y=_______.
7.已知x的平方根是±8,则x的立方根是________.
二、选一选:
8.4的平方根是(
)
A.2
B.-2
C.±2
D.±9.下列各式中,无意义的是(
)
A.-
B.
C.
D.
10.下列各组数中,互为相反数的一组是(
)
A.-2与
B.-2与
C.-2与-
D.│-2│与2
11.
下列说法正确的是
(
)
A.1的平方根是1;
B.1的算术平方根是1;
C.-2是2的平方根;
D.-1的平方根是-1
三、做一做:
12.
求下列各数的平方根:
(1)81;(2);(3)1.44;(4)2;
(5).
13.
求下列各式中的x:
①x2=1.21;
②27(x+1)3+64=0.
14.
a≥0时,才有意义——表示a的算术平方根.由此你会求下列各式有意义时x的取值范围吗?试试看:
(1)
(2)
(3)
(4)
+
15.已知2a-1的平方根是±3,3a+b-1的平方根是±4,求a+2b的平方根.
