广东省佛山市高明区北师大版2020-2021学年第二学期八年级数学周测试题(Word版,附答案)
文档属性
| 名称 | 广东省佛山市高明区北师大版2020-2021学年第二学期八年级数学周测试题(Word版,附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 418.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 15:55:58 | ||
图片预览



文档简介
2020-2021第二学期八年级数学周测试题(2021.3.3)
一、选择题(每小题3分,共30分)
1.下面给出的几种三角形中不一定为等边三角形的是(
)
A.
有两个角为60°的三角形
B.
有一个角为60°的等腰三角形
C.
一边上的高也是这边上的中线的等腰三角形
D.
有一个角是60°且是轴对称的三角形;
2.
如图,一艘海轮位于灯塔P的南偏西65°方向的A处,它以每小时36海里的速度向正北方向航行,1.5小时后到达位于灯塔P的北偏东50°的B处,则B处与灯塔P的距离为( )
A.
48海里
B.52海里
C.
54海里
D.
64海里
第5题图
第6题图
3.
用反证法证明“三角形中至少有一个内角不小于60°”,应先假设这个三角形中(
)
A.
有一个内角小于60°
B.
每一个内角都小于60°
C.
有一个内角大于60°
D.
每一个内角都大于60°
4.下列说法中,能判定两个直角三角形全等的个数有(
)
①斜边和一锐角分别相等;
②斜边和一直角边对应相等;
③一个锐角和一条边分别相等;
④两边分别相等;
⑤两个锐角分别相等;
⑥一条直角边相等且另一条直角边上的中线相等;
A.3
B.4
C.5
D.6
5.如图,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=6cm,则AC=(
)
A.6cm
B.5cm
C.4cm
D.3cm
6.如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为( )
A.4.5
B.5
C.5.5
D.6
7.如图,△ABC中,∠ACB=90°,∠CAB=60°,动点P在斜边AB所在的直线m上运动,连结PC,那点P在直线m上运动时,能使图中出现等腰三角形的点P的位置有( )
A.6个
B.5个
C.4个
D.3个
8.如图,等边△ABC中,AB=4,点P在边AB上,PD⊥BC,DE⊥AC,垂足分别为D、E,设PA=x,若用含x的式子表示AE的长,正确的是(
)
A.2﹣x
B.3﹣x
C.1
D.2+x
第7题图
第8题图
第10题图
9.
下列命题:
①等腰三角形的高、中线、角平分线三线合一;
②等腰三角形一定是锐角三角形;
③等腰三角形一腰上的高与底边的夹角度数等于这个三角形顶角度数的一半;
④在同一个三角形中,等角对等边.
其中真命题的个数是(
)
A.1个
B.2个
C.3个
D.4个
10.如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若,则△A6B6A7的边长为( )
A.6
B.12
C.16
D.32
二、填空题(每小题4分,共28分)
11.命题“全等三角形的对应角相等”的逆命题是
.
12.如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,若利用“HL”证明Rt△ABC≌Rt△DCB,你添加的条件是
.(不添加字母和辅助线)
第12题图
第13题图
第14题图
13.
如图,一棵树在一次强台风中于离地面4米处折断倒下,倒下部分与地面成30°夹角,这棵树在折断前的高度为______米。
14.如图,在Rt△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,CD=2,则BC=
.
15.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=
.
16.如图,在△ABC中,D,E分别在边CB和BC的延长线上,BD=BA,CE=CA,若∠BAC=50°,则∠DAE=
.
17.
如图,在△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,BD与CE相交于点O,连接AO,有如下命题:①∠1=∠2;②OE=OD;③∠3=∠4;④AD=DC;⑤AO所在的直线是线段BC的对称轴.其中是真命题的个数为
(填真命题的序号)
.
2020-2021第二学期八年级数学周测试题答题卡(2021.3.7)
班级:
学号:
姓名:
成绩:
一、选择题(30分):
题号
1
2
3
4
5
6
7
8
9
10
答案
二填空题(28分):
12.
14.
15.
16.
17.
三、解答题(共62分)
18.(8分)
用反证法证明:等腰三角形的底角必为锐角.
19.(10分)如图,△ABC中,AB=AC,AB的垂直平分线DE分别交AC、AB于点D、E.
(1)若∠A=50°,求∠CBD的度数;
(2)若AB=7,△CBD周长为12,求BC的长.
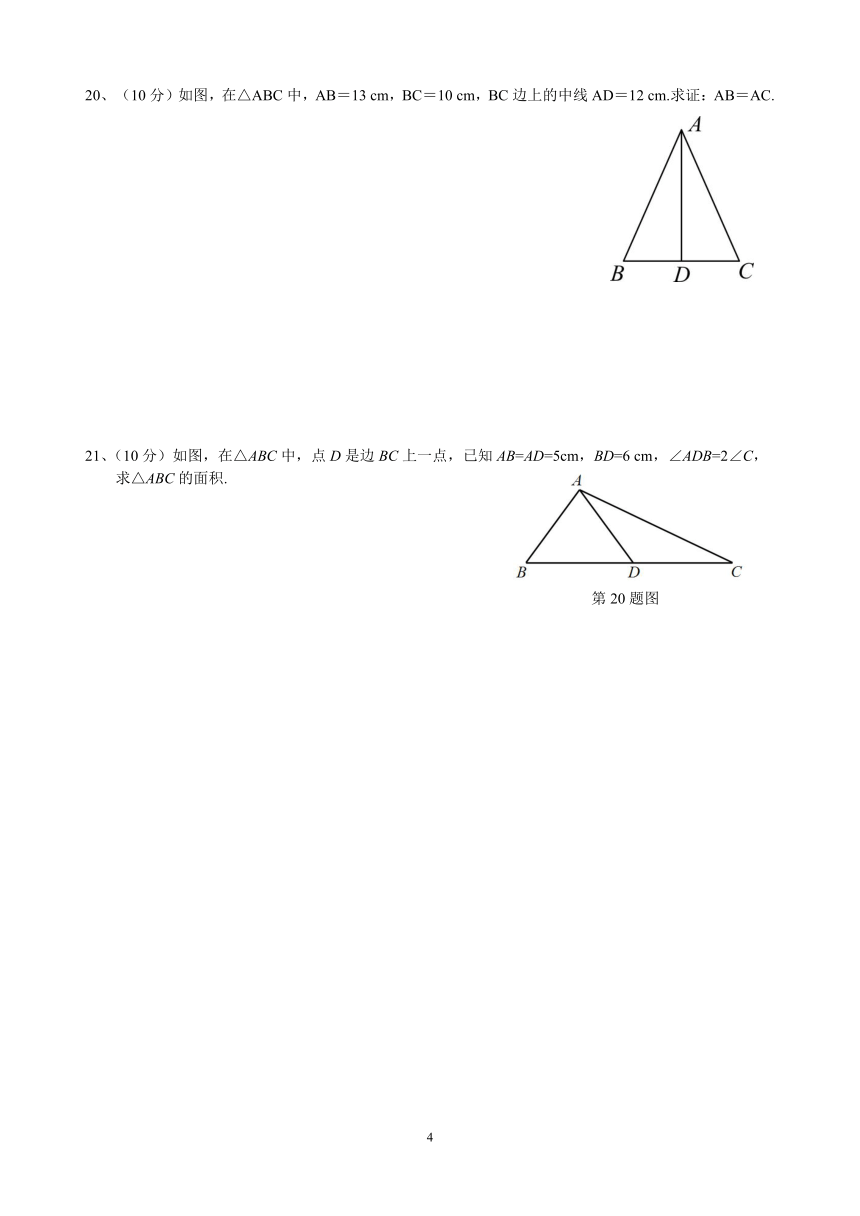
(10分)如图,在△ABC中,AB=13
cm,BC=10
cm,BC边上的中线AD=12
cm.求证:AB=AC.
21、(10分)如图,在△ABC中,点D是边BC上一点,已知AB=AD=5cm,BD=6
cm,∠ADB=2∠C,
求△ABC的面积.
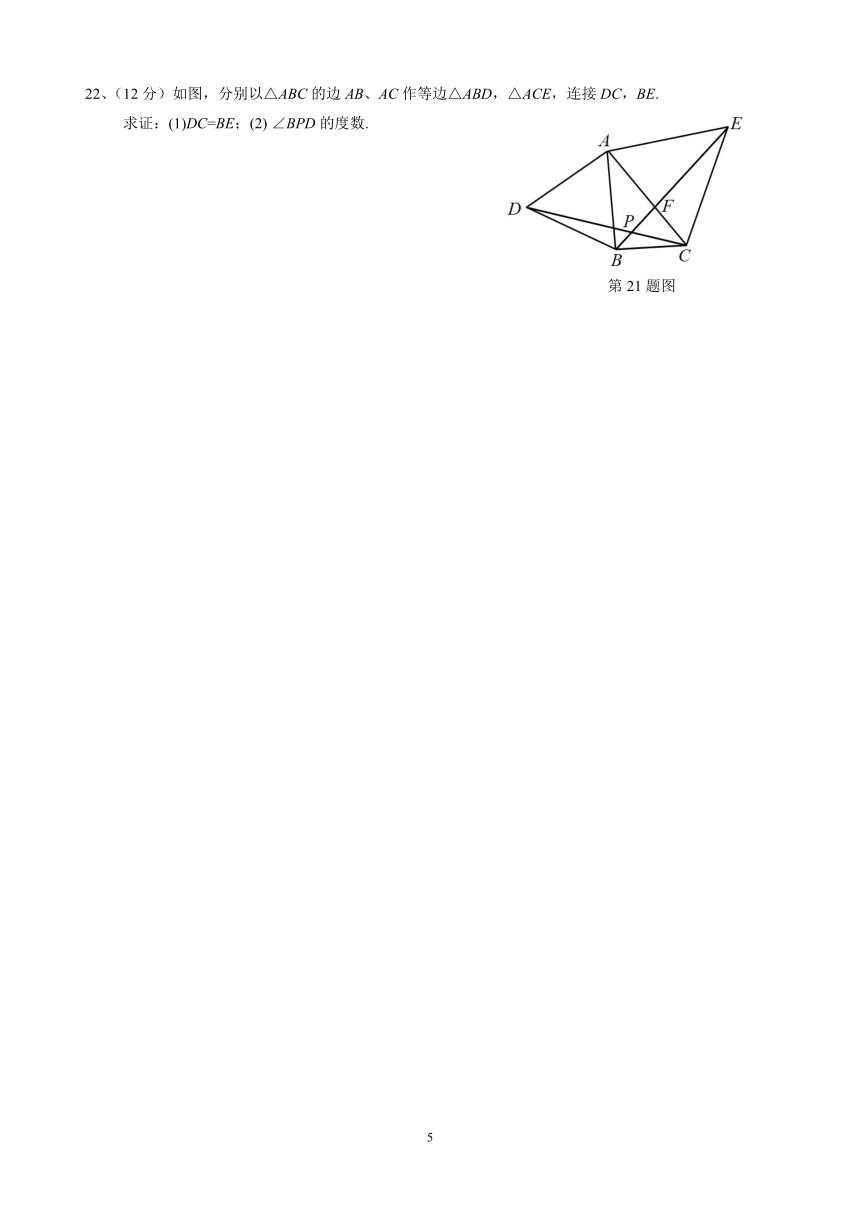
22、(12分)如图,分别以△ABC的边AB、AC作等边△ABD,△ACE,连接DC,BE.
求证:(1)DC=BE;(2)
∠BPD的度数.
23.(12分)在△ABC中,AB=AC,∠B=30°,点P在BC边上运动(P不与B、C重合),连接AP,作∠APQ=∠B,PQ交AB于点Q.
(1)如图1,当PQ∥CA时,判断△APB的形状并说明理由;
(2)在点P的运动过程中,△APQ的形状可以是等腰三角形吗?若可以,请直接写出∠BQP的度数;若不可以,请说明理由.
2020-2021第二学期八年级数学周测试题答案(2021.3.7)
班级:
学号:
姓名:
成绩:
一、选择题(30分):
题号
1
2
3
4
5
6
7
8
9
10
答案
C
C
B
B
D
C
C
B
B
C
10.解:∵△A1B1A2是等边三角形,
∴A1B1=A2B1,∠3=∠4=∠12=60°,
∴∠2=120°,
∵∠MON=30°,
∴∠1=180°﹣120°﹣30°=30°,
又∵∠3=60°,
∴∠5=180°﹣60°﹣30°=90°,
∵∠MON=∠1=30°,
∴OA1=A1B1=,
∴A2B1=,
∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,
∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A2B2=2B1A2,B3A3=2B2A3,
∴A3B3=4B1A2=2,
A4B4=8B1A2=4,
A5B5=16B1A2=8,…
∴△AnBnAn+1的边长为×2n﹣1,
∴△A6B6A7的边长为×26﹣1=×25=16.
故选:C.
二填空题(28分):
对应角相等的三角形是全等三角形
12.
AB=DC(答案不唯一,
AC=DB也可以)
12
14.
6
15.
5
16.
115°
17.
①②③⑤
15.
解:过P作PD⊥OB,交OB于点D,
在Rt△OPD中,∠POD=600,则∠OPD=300
,
OP=12,
∴OD=6,
∵PM=PN,PD⊥MN,MN=2,
∴MD=ND=MN=1,
∴OM=OD﹣MD=6﹣1=5.
故答案为:5.
16.解:∵AB=BD,AC=CE,
∴∠BAD=∠BDA,∠E=∠CAE,
设∠BAD=∠BDA=x,∠E=∠CAE=y,
∴∠ABC=∠BAD+∠BDA=2x,∠ACB=∠E+∠CAE=2y,
∵∠ABC+∠ACB+∠BAC=180°,
∴2x+2y+50°=180°,
∴x+y=65°,
∴∠DAE=∠DAB+∠CAE+∠BAC=65°+50°=115°.
故答案为:115°.
三、解答题(共62分)
18.(8分)
用反证法证明:等腰三角形的底角必为锐角.
证明:
假设等腰三角形的底角∠B,∠C不是锐角,即∠B=∠C≥90°.
则∠A+∠B+∠C>180°,
这与三角形的内角和定理相矛盾,所以假设不成立.
故∠B、∠C必为锐角,即等腰三角形的底角必为锐角.
19.(10分)如图,△ABC中,AB=AC,AB的垂直平分线DE分别交AC、AB于点D、E.
(1)若∠A=50°,求∠CBD的度数;
(2)若AB=7,△CBD周长为12,求BC的长.
解:(1)∵AB=AC,∠A=50°,
∴∠ABC=∠C=65°,
又∵DE垂直平分AB,
∴DA=DB,
∴∠ABD=∠A=50°,
∴∠DBC=15°;
(2)∵DE垂直平分AB,
∴DA=DB,
∴DB+DC=DA+DC=AC,
又∵AB=AC=7,△CBD周长为12,
∴BC=5.
(10分)如图,在△ABC中,AB=13
cm,BC=10
cm,BC边上的中线AD=12
cm.
求证:AB=AC.
证明:∵AD是BC边上的中线,
BC=10
cm
∴BD=CD=
BC=5
cm
在△ABD中,AD2+BD2=144+25=169,
AB2=132=169
∴AD2+BD2=AB2
∴∠ADB=90°,
∴∠ADC=90°
∴AC=13(cm),
∴AB=AC
21.
(10分)如图,在△ABC中,点D是边BC上一点,已知AB=AD=5cm,BD=6
cm,∠ADB=2∠C,
求△ABC的面积.
解:过点A作AG⊥BC,垂足为G,
∴点G为BD的中点(等腰三角形的三线合一),
∵BD=6,∴BG
=DG
==3
cm,
在Rt△ABG中,AG=(cm),
又∵∠ADB=∠C
+∠DAC,
∠ADB=2∠C,
∴∠C
+∠DAC=2∠C,
∴∠C
=∠DAC,
∴DC=DA=5
cm,
∴BC=BD+DC=6+5=11(
cm),
∴△ABC的面积为=22(cm)2.
22、(12分)如图,分别以△ABC的边AB、AC作等边△ABD,△ACE,连接DC,BE.
求证:(1)DC=BE;
(2)
∠BPD的度数.
证明:(1) ∵△ABD,△ACE都是等边三角形,
∴AD=AB,AC=AE,∠DAB=∠CAE=60°,
∵∠DAB+∠BAC=∠CAE+∠BAC,
即:∠DAC=∠BAE,
在△DAC和△BAE中,
∵
∴△DAC≌△BAE(SAS),
∴DC=BE;
(2)由△DAC≌△BAE得,
∠ACD=∠AEB
∵∠AFE=∠BFC
∴∠CPF=∠AFE=60°,
∴∠DPB=∠CPF=60°.
23.(12分)在△ABC中,AB=AC,∠B=30°,点P在BC边上运动(P不与B、C重合),连接AP,作∠APQ=∠B,PQ交AB于点Q.
(1)如图1,当PQ∥CA时,判断△APB的形状并说明理由;
(2)在点P的运动过程中,△APQ的形状可以是等腰三角形吗?若可以,请直接写出∠BQP的度数;若不可以,请说明理由.
解:(1)△APB是直角三角形,
理由如下:
∵AB=AC,∠B=30°,
∴∠C=30°=∠B=∠APQ,
∵PQ∥AC,
∴∠BPQ=∠C,
∴∠APB=60°,
∴∠BAP=90°,
∴△APB是直角三角形;
(2)当AQ=QP时,
∴∠QAP=∠APQ=30°,
∴∠BQP=∠QAP+∠APQ=60°,
当AP=PQ时,则∠AQP=∠PAQ=75°,
∴∠BQP=105°,
当AQ=AP时,则∠AQP=∠APQ=30°,
∵P不与B、C重合,
∴不存在,
综上所述:∠BQP=105°或60°.
第2题图
第16题图
第17题图
第15题图
第20题图
第21题图
第21题图
第21题图
第22题图
一、选择题(每小题3分,共30分)
1.下面给出的几种三角形中不一定为等边三角形的是(
)
A.
有两个角为60°的三角形
B.
有一个角为60°的等腰三角形
C.
一边上的高也是这边上的中线的等腰三角形
D.
有一个角是60°且是轴对称的三角形;
2.
如图,一艘海轮位于灯塔P的南偏西65°方向的A处,它以每小时36海里的速度向正北方向航行,1.5小时后到达位于灯塔P的北偏东50°的B处,则B处与灯塔P的距离为( )
A.
48海里
B.52海里
C.
54海里
D.
64海里
第5题图
第6题图
3.
用反证法证明“三角形中至少有一个内角不小于60°”,应先假设这个三角形中(
)
A.
有一个内角小于60°
B.
每一个内角都小于60°
C.
有一个内角大于60°
D.
每一个内角都大于60°
4.下列说法中,能判定两个直角三角形全等的个数有(
)
①斜边和一锐角分别相等;
②斜边和一直角边对应相等;
③一个锐角和一条边分别相等;
④两边分别相等;
⑤两个锐角分别相等;
⑥一条直角边相等且另一条直角边上的中线相等;
A.3
B.4
C.5
D.6
5.如图,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=6cm,则AC=(
)
A.6cm
B.5cm
C.4cm
D.3cm
6.如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为( )
A.4.5
B.5
C.5.5
D.6
7.如图,△ABC中,∠ACB=90°,∠CAB=60°,动点P在斜边AB所在的直线m上运动,连结PC,那点P在直线m上运动时,能使图中出现等腰三角形的点P的位置有( )
A.6个
B.5个
C.4个
D.3个
8.如图,等边△ABC中,AB=4,点P在边AB上,PD⊥BC,DE⊥AC,垂足分别为D、E,设PA=x,若用含x的式子表示AE的长,正确的是(
)
A.2﹣x
B.3﹣x
C.1
D.2+x
第7题图
第8题图
第10题图
9.
下列命题:
①等腰三角形的高、中线、角平分线三线合一;
②等腰三角形一定是锐角三角形;
③等腰三角形一腰上的高与底边的夹角度数等于这个三角形顶角度数的一半;
④在同一个三角形中,等角对等边.
其中真命题的个数是(
)
A.1个
B.2个
C.3个
D.4个
10.如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若,则△A6B6A7的边长为( )
A.6
B.12
C.16
D.32
二、填空题(每小题4分,共28分)
11.命题“全等三角形的对应角相等”的逆命题是
.
12.如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,若利用“HL”证明Rt△ABC≌Rt△DCB,你添加的条件是
.(不添加字母和辅助线)
第12题图
第13题图
第14题图
13.
如图,一棵树在一次强台风中于离地面4米处折断倒下,倒下部分与地面成30°夹角,这棵树在折断前的高度为______米。
14.如图,在Rt△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,CD=2,则BC=
.
15.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=
.
16.如图,在△ABC中,D,E分别在边CB和BC的延长线上,BD=BA,CE=CA,若∠BAC=50°,则∠DAE=
.
17.
如图,在△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,BD与CE相交于点O,连接AO,有如下命题:①∠1=∠2;②OE=OD;③∠3=∠4;④AD=DC;⑤AO所在的直线是线段BC的对称轴.其中是真命题的个数为
(填真命题的序号)
.
2020-2021第二学期八年级数学周测试题答题卡(2021.3.7)
班级:
学号:
姓名:
成绩:
一、选择题(30分):
题号
1
2
3
4
5
6
7
8
9
10
答案
二填空题(28分):
12.
14.
15.
16.
17.
三、解答题(共62分)
18.(8分)
用反证法证明:等腰三角形的底角必为锐角.
19.(10分)如图,△ABC中,AB=AC,AB的垂直平分线DE分别交AC、AB于点D、E.
(1)若∠A=50°,求∠CBD的度数;
(2)若AB=7,△CBD周长为12,求BC的长.
(10分)如图,在△ABC中,AB=13
cm,BC=10
cm,BC边上的中线AD=12
cm.求证:AB=AC.
21、(10分)如图,在△ABC中,点D是边BC上一点,已知AB=AD=5cm,BD=6
cm,∠ADB=2∠C,
求△ABC的面积.
22、(12分)如图,分别以△ABC的边AB、AC作等边△ABD,△ACE,连接DC,BE.
求证:(1)DC=BE;(2)
∠BPD的度数.
23.(12分)在△ABC中,AB=AC,∠B=30°,点P在BC边上运动(P不与B、C重合),连接AP,作∠APQ=∠B,PQ交AB于点Q.
(1)如图1,当PQ∥CA时,判断△APB的形状并说明理由;
(2)在点P的运动过程中,△APQ的形状可以是等腰三角形吗?若可以,请直接写出∠BQP的度数;若不可以,请说明理由.
2020-2021第二学期八年级数学周测试题答案(2021.3.7)
班级:
学号:
姓名:
成绩:
一、选择题(30分):
题号
1
2
3
4
5
6
7
8
9
10
答案
C
C
B
B
D
C
C
B
B
C
10.解:∵△A1B1A2是等边三角形,
∴A1B1=A2B1,∠3=∠4=∠12=60°,
∴∠2=120°,
∵∠MON=30°,
∴∠1=180°﹣120°﹣30°=30°,
又∵∠3=60°,
∴∠5=180°﹣60°﹣30°=90°,
∵∠MON=∠1=30°,
∴OA1=A1B1=,
∴A2B1=,
∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,
∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A2B2=2B1A2,B3A3=2B2A3,
∴A3B3=4B1A2=2,
A4B4=8B1A2=4,
A5B5=16B1A2=8,…
∴△AnBnAn+1的边长为×2n﹣1,
∴△A6B6A7的边长为×26﹣1=×25=16.
故选:C.
二填空题(28分):
对应角相等的三角形是全等三角形
12.
AB=DC(答案不唯一,
AC=DB也可以)
12
14.
6
15.
5
16.
115°
17.
①②③⑤
15.
解:过P作PD⊥OB,交OB于点D,
在Rt△OPD中,∠POD=600,则∠OPD=300
,
OP=12,
∴OD=6,
∵PM=PN,PD⊥MN,MN=2,
∴MD=ND=MN=1,
∴OM=OD﹣MD=6﹣1=5.
故答案为:5.
16.解:∵AB=BD,AC=CE,
∴∠BAD=∠BDA,∠E=∠CAE,
设∠BAD=∠BDA=x,∠E=∠CAE=y,
∴∠ABC=∠BAD+∠BDA=2x,∠ACB=∠E+∠CAE=2y,
∵∠ABC+∠ACB+∠BAC=180°,
∴2x+2y+50°=180°,
∴x+y=65°,
∴∠DAE=∠DAB+∠CAE+∠BAC=65°+50°=115°.
故答案为:115°.
三、解答题(共62分)
18.(8分)
用反证法证明:等腰三角形的底角必为锐角.
证明:
假设等腰三角形的底角∠B,∠C不是锐角,即∠B=∠C≥90°.
则∠A+∠B+∠C>180°,
这与三角形的内角和定理相矛盾,所以假设不成立.
故∠B、∠C必为锐角,即等腰三角形的底角必为锐角.
19.(10分)如图,△ABC中,AB=AC,AB的垂直平分线DE分别交AC、AB于点D、E.
(1)若∠A=50°,求∠CBD的度数;
(2)若AB=7,△CBD周长为12,求BC的长.
解:(1)∵AB=AC,∠A=50°,
∴∠ABC=∠C=65°,
又∵DE垂直平分AB,
∴DA=DB,
∴∠ABD=∠A=50°,
∴∠DBC=15°;
(2)∵DE垂直平分AB,
∴DA=DB,
∴DB+DC=DA+DC=AC,
又∵AB=AC=7,△CBD周长为12,
∴BC=5.
(10分)如图,在△ABC中,AB=13
cm,BC=10
cm,BC边上的中线AD=12
cm.
求证:AB=AC.
证明:∵AD是BC边上的中线,
BC=10
cm
∴BD=CD=
BC=5
cm
在△ABD中,AD2+BD2=144+25=169,
AB2=132=169
∴AD2+BD2=AB2
∴∠ADB=90°,
∴∠ADC=90°
∴AC=13(cm),
∴AB=AC
21.
(10分)如图,在△ABC中,点D是边BC上一点,已知AB=AD=5cm,BD=6
cm,∠ADB=2∠C,
求△ABC的面积.
解:过点A作AG⊥BC,垂足为G,
∴点G为BD的中点(等腰三角形的三线合一),
∵BD=6,∴BG
=DG
==3
cm,
在Rt△ABG中,AG=(cm),
又∵∠ADB=∠C
+∠DAC,
∠ADB=2∠C,
∴∠C
+∠DAC=2∠C,
∴∠C
=∠DAC,
∴DC=DA=5
cm,
∴BC=BD+DC=6+5=11(
cm),
∴△ABC的面积为=22(cm)2.
22、(12分)如图,分别以△ABC的边AB、AC作等边△ABD,△ACE,连接DC,BE.
求证:(1)DC=BE;
(2)
∠BPD的度数.
证明:(1) ∵△ABD,△ACE都是等边三角形,
∴AD=AB,AC=AE,∠DAB=∠CAE=60°,
∵∠DAB+∠BAC=∠CAE+∠BAC,
即:∠DAC=∠BAE,
在△DAC和△BAE中,
∵
∴△DAC≌△BAE(SAS),
∴DC=BE;
(2)由△DAC≌△BAE得,
∠ACD=∠AEB
∵∠AFE=∠BFC
∴∠CPF=∠AFE=60°,
∴∠DPB=∠CPF=60°.
23.(12分)在△ABC中,AB=AC,∠B=30°,点P在BC边上运动(P不与B、C重合),连接AP,作∠APQ=∠B,PQ交AB于点Q.
(1)如图1,当PQ∥CA时,判断△APB的形状并说明理由;
(2)在点P的运动过程中,△APQ的形状可以是等腰三角形吗?若可以,请直接写出∠BQP的度数;若不可以,请说明理由.
解:(1)△APB是直角三角形,
理由如下:
∵AB=AC,∠B=30°,
∴∠C=30°=∠B=∠APQ,
∵PQ∥AC,
∴∠BPQ=∠C,
∴∠APB=60°,
∴∠BAP=90°,
∴△APB是直角三角形;
(2)当AQ=QP时,
∴∠QAP=∠APQ=30°,
∴∠BQP=∠QAP+∠APQ=60°,
当AP=PQ时,则∠AQP=∠PAQ=75°,
∴∠BQP=105°,
当AQ=AP时,则∠AQP=∠APQ=30°,
∵P不与B、C重合,
∴不存在,
综上所述:∠BQP=105°或60°.
第2题图
第16题图
第17题图
第15题图
第20题图
第21题图
第21题图
第21题图
第22题图
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
