2020-2021学年七年级数学人教版下册6.1平方根-课件(共15张ppt)
文档属性
| 名称 | 2020-2021学年七年级数学人教版下册6.1平方根-课件(共15张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 540.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 15:43:29 | ||
图片预览

文档简介
(共15张PPT)
课题:算术平方根
难点名称:算术平方根的概念及求法
1
义务教育教科书(数学)七年级下册第六章第一节
目录
CONTENTS
2
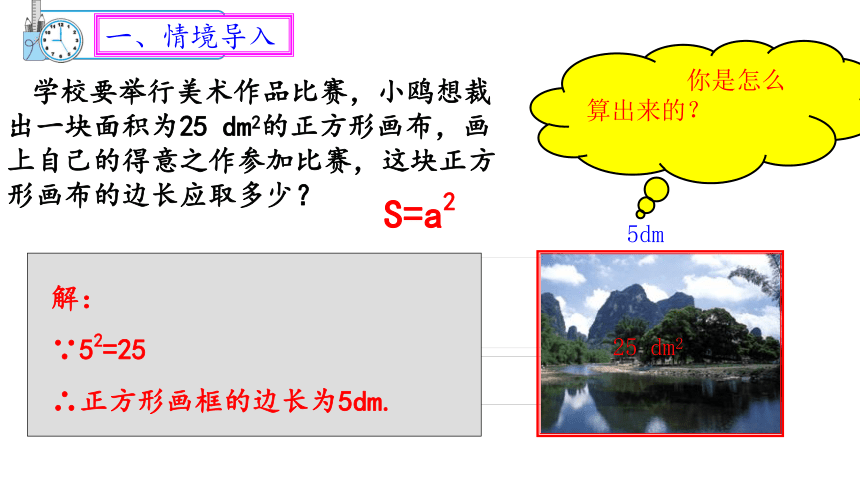
一、情境导入
你是怎么算出来的?
学校要举行美术作品比赛,小鸥想裁出一块面积为25
dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
解:
∵52=25
∴正方形画框的边长为5dm.
5dm
25
dm2
S=a2
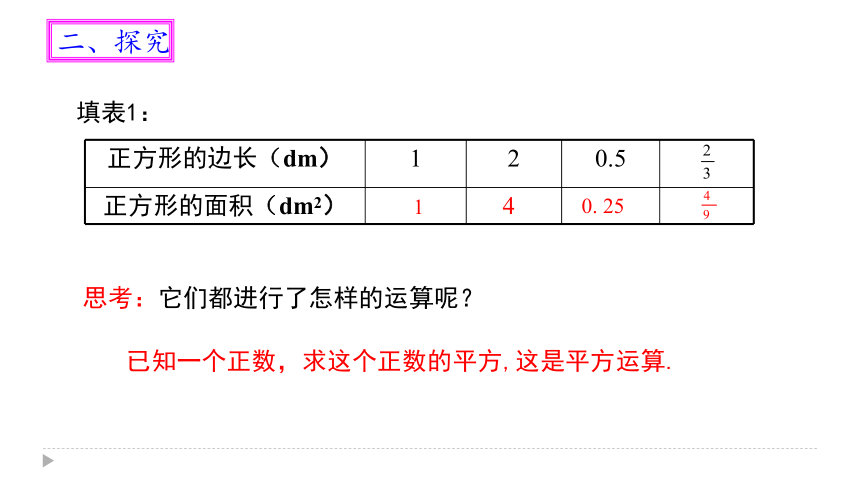
已知一个正数,求这个正数的平方,这是平方运算.
正方形的边长(dm)
1
2
0.5
正方形的面积(dm2)
1
填表1:
思考:它们都进行了怎样的运算呢?
4
0.
25
二、探究
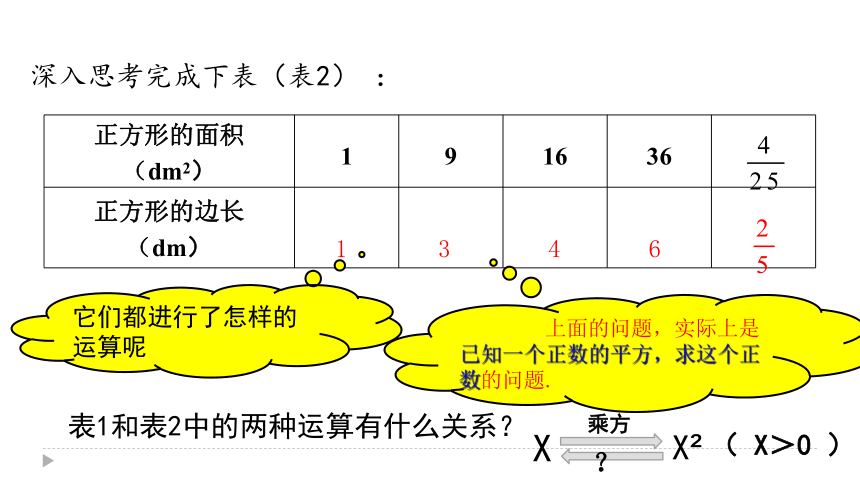
深入思考完成下表(表2)
:
正方形的面积
(dm2)
1
9
16
36
正方形的边长
(dm)
1
3
4
6
它们都进行了怎样的运算呢
上面的问题,实际上是已知一个正数的平方,求这个正数的问题.
表1和表2中的两种运算有什么关系?
X
X?
乘方
?
(
X>0
)
根号
被开方数
算术平方根
a
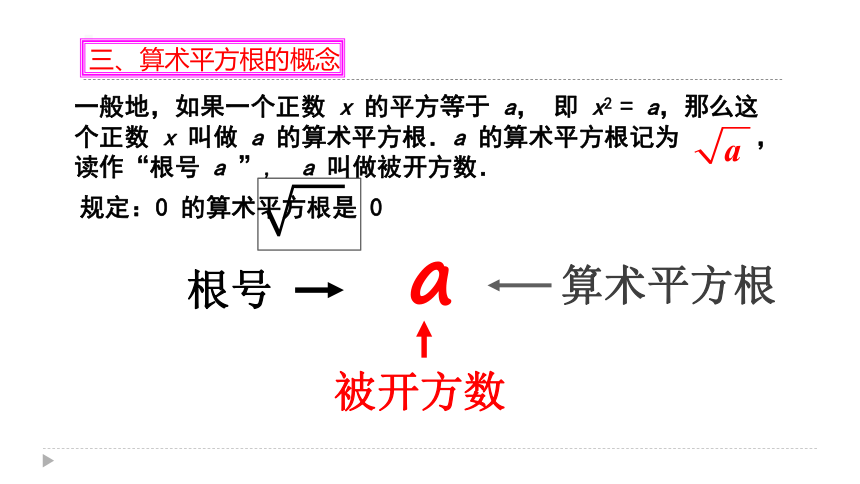
三、算术平方根的概念
一般地,如果一个正数
x
的平方等于
a,
即
x2
=
a,那么这个正数
x
叫做
a
的算术平方根.a
的算术平方根记为
,读作“根号
a
”,
a
叫做被开方数.
规定:0
的算术平方根是
0.
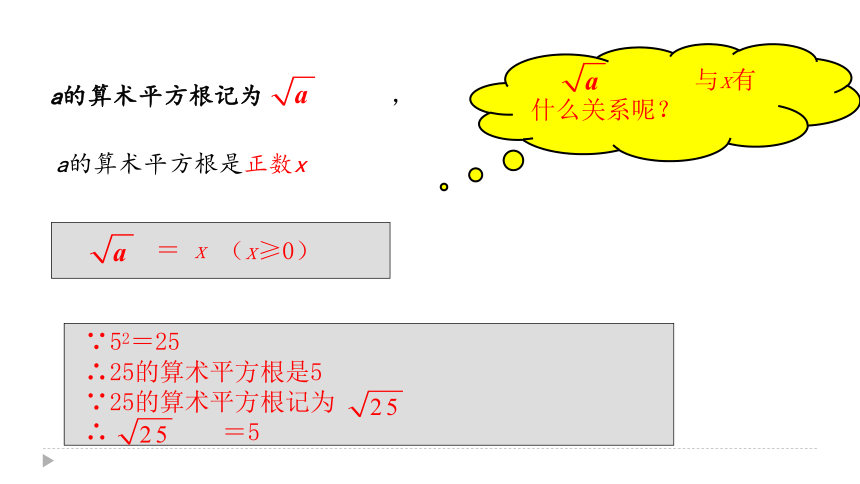
与x有什么关系呢?
a的算术平方根记为
,
a的算术平方根是正数x
=
x
(x≥0)
∵52=25
∴25的算术平方根是5
∵25的算术平方根记为
∴
=5
四、应用提高
=
x
(x≥0)
例1:求下列各数的算术平方根:
(1)100;(2)
;(3)0.000
1.
解:(1)因为102=100,
所以100的算术平方根是10.
即
.
=
x
(x≥0)
例1:求下列各数的算术平方根:
(1)100;(2)
;(3)0.000
1.
解:(2)因为
,
所以
的算术平方根是
.
即
.
应用提高
=
x
(x≥0)
例1:求下列各数的算术平方根:
(1)100;(2)
;(3)0.000
1.
解:(3)因为0.012=0.000
1,
所以0.000
1的算术平方根是0.01.
即
.
应用提高
=
x
(x≥0)
例1:求下列各数的算术平方根:
(1)100;(2)
;(3)0.000
1.
被开方数越大,
对应的算术平方根也越大
被开方数的大小与对应的算术平方根的大小之间有什么关系呢?
负数有算术平方根吗?
负数没有算术平方根
即:被开方数是非负数
(a≥0)
应用提高
例2:下列各式有意义吗?为什么.
解:(1)
无意义,负数没有算术平方根;
(2)
有意义,表示5的算术平方根的相反数;
(3)
有意义,表示
(-5)2
的算术平方根.
25
应用提高
?
1、
想一想:下列式子表示什么意思?你能求出它们的值吗?
解:(1)
表示49的算术平方根,
(2)
表示112的算术平方根,
(3)
表示
的算术平方根,
(4)
表示0的算术平方根,
五、应用提高
?
2、正数a的算术平方根记为____,读作“____
”,
a叫做
________.
3、0
的算术平方根是__.
算术平方根
根号a
被开方数
0
课堂小结
a
4、被开方数越大,对应的算术平方根也越大
谢谢!
课题:算术平方根
难点名称:算术平方根的概念及求法
1
义务教育教科书(数学)七年级下册第六章第一节
目录
CONTENTS
2
一、情境导入
你是怎么算出来的?
学校要举行美术作品比赛,小鸥想裁出一块面积为25
dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
解:
∵52=25
∴正方形画框的边长为5dm.
5dm
25
dm2
S=a2
已知一个正数,求这个正数的平方,这是平方运算.
正方形的边长(dm)
1
2
0.5
正方形的面积(dm2)
1
填表1:
思考:它们都进行了怎样的运算呢?
4
0.
25
二、探究
深入思考完成下表(表2)
:
正方形的面积
(dm2)
1
9
16
36
正方形的边长
(dm)
1
3
4
6
它们都进行了怎样的运算呢
上面的问题,实际上是已知一个正数的平方,求这个正数的问题.
表1和表2中的两种运算有什么关系?
X
X?
乘方
?
(
X>0
)
根号
被开方数
算术平方根
a
三、算术平方根的概念
一般地,如果一个正数
x
的平方等于
a,
即
x2
=
a,那么这个正数
x
叫做
a
的算术平方根.a
的算术平方根记为
,读作“根号
a
”,
a
叫做被开方数.
规定:0
的算术平方根是
0.
与x有什么关系呢?
a的算术平方根记为
,
a的算术平方根是正数x
=
x
(x≥0)
∵52=25
∴25的算术平方根是5
∵25的算术平方根记为
∴
=5
四、应用提高
=
x
(x≥0)
例1:求下列各数的算术平方根:
(1)100;(2)
;(3)0.000
1.
解:(1)因为102=100,
所以100的算术平方根是10.
即
.
=
x
(x≥0)
例1:求下列各数的算术平方根:
(1)100;(2)
;(3)0.000
1.
解:(2)因为
,
所以
的算术平方根是
.
即
.
应用提高
=
x
(x≥0)
例1:求下列各数的算术平方根:
(1)100;(2)
;(3)0.000
1.
解:(3)因为0.012=0.000
1,
所以0.000
1的算术平方根是0.01.
即
.
应用提高
=
x
(x≥0)
例1:求下列各数的算术平方根:
(1)100;(2)
;(3)0.000
1.
被开方数越大,
对应的算术平方根也越大
被开方数的大小与对应的算术平方根的大小之间有什么关系呢?
负数有算术平方根吗?
负数没有算术平方根
即:被开方数是非负数
(a≥0)
应用提高
例2:下列各式有意义吗?为什么.
解:(1)
无意义,负数没有算术平方根;
(2)
有意义,表示5的算术平方根的相反数;
(3)
有意义,表示
(-5)2
的算术平方根.
25
应用提高
?
1、
想一想:下列式子表示什么意思?你能求出它们的值吗?
解:(1)
表示49的算术平方根,
(2)
表示112的算术平方根,
(3)
表示
的算术平方根,
(4)
表示0的算术平方根,
五、应用提高
?
2、正数a的算术平方根记为____,读作“____
”,
a叫做
________.
3、0
的算术平方根是__.
算术平方根
根号a
被开方数
0
课堂小结
a
4、被开方数越大,对应的算术平方根也越大
谢谢!
