2020-2021学年人教版九年级数学下册 课件28.2第2课时 与方向角、坡度有关的解直角三角形的应用(共16张ppt)
文档属性
| 名称 | 2020-2021学年人教版九年级数学下册 课件28.2第2课时 与方向角、坡度有关的解直角三角形的应用(共16张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 839.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 15:40:40 | ||
图片预览





文档简介
(共16张PPT)
第2课时 与方向角、坡度有关的解直角三角形的应用
一、教学目标
二、教学重难点
重点
难点
1.了解什么是方位角、坡度及方位角的命名特点,准确熟练解决有关方位角问题.
2.巩固用解直角三角形有关知识解决实际问题的方法.
运用解直角三角形解决航行、斜坡问题.
灵活运用解直角三角形的方法解决生活中的实际问题.
活动1
新课导入
三、教学设计
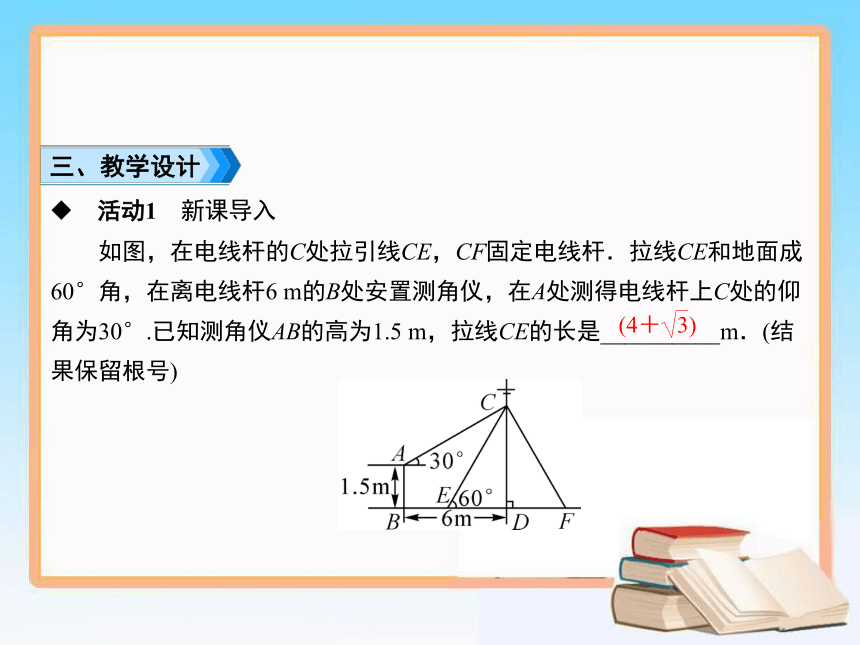
如图,在电线杆的C处拉引线CE,CF固定电线杆.拉线CE和地面成60°角,在离电线杆6
m的B处安置测角仪,在A处测得电线杆上C处的仰角为30°.已知测角仪AB的高为1.5
m,拉线CE的长是__________m.(结果保留根号)
活动2
探究新知
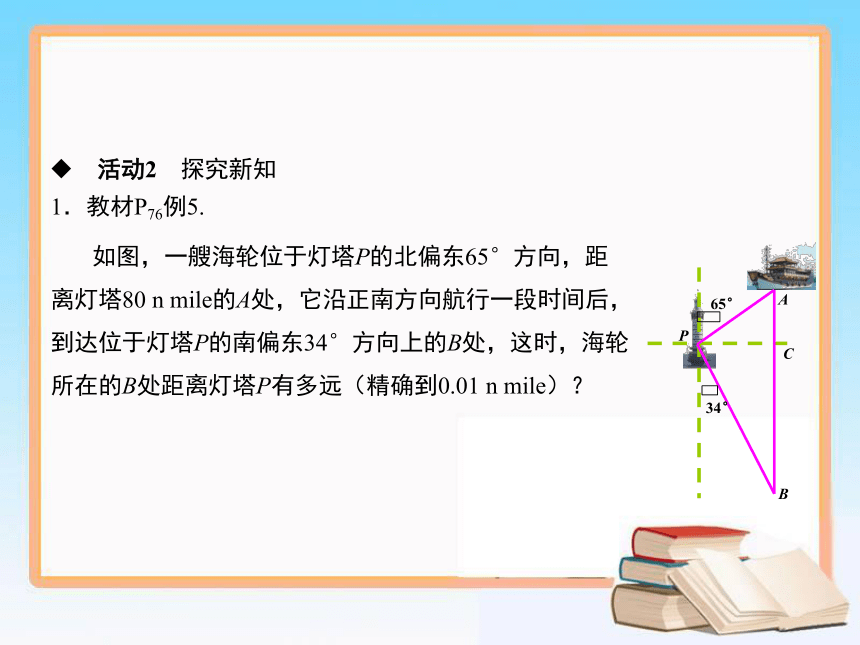
如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80
n
mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(精确到0.01
n
mile)?
65°
34°
P
B
C
A
1.教材P76例5.
解:如图
,在Rt△APC中,
PC=PA·cos(90°-65°)
=80×cos25°
≈80×0.91
=72.8
在Rt△BPC中,∠B=34°
当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130.23n
mile.
65°
34°
P
B
C
A
2.如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6
m,坝高20
m,斜坡AB的坡度i=1∶2.5,斜坡CD的坡角为30°.求坝底AD的长度.(精确到0.1
m,参考数据:
)
答:坝底AD的长度为90.64
m.
≈1.414,
≈1.732
活动3
知识归纳
1.坡度、坡角概念.
如图,BC表示水平面,AB表示坡面,把水平面BC与坡面AB形成的角∠ABC称为坡角α,坡面的铅直高度h与水平宽度l的比叫做坡面的坡度(或坡比),记作i=
=tan
α.
2.利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为________问题(画出平面图形,转化为解直角三角形的问题);
(2)根据问题中的条件,适当选用锐角三角函数等解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
数学
活动4
例题与练习
例1 如图,海中一小岛A,该岛四周10
n
mile内有暗礁,今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20
n
mile后到达该岛的南偏西25°的C处之后,货轮继续向东航行,你认为货轮向东航行的途中会有触礁的危险吗?
解:过点A作AD⊥BC交BC的延长线于点D.
由题意,得∠BAD=55°,∠CAD=25°,BC=20
n
mile.在Rt△ABD中,
∴BD=AD·tan
55°.在Rt△ACD中,
∴CD=AD·tan
25°.
∵BD=BC+CD,
∴AD·tan
55°=20+AD·tan
25°,
答:轮船继续向东行驶,不会有触礁危险.
≈20.79(n
mile)>10(n
mile).
例2 如图,水库大坝的横断面是梯形,坝顶宽6
m,坝高23
m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,求斜坡AB的坡角α,坝底宽AD和斜坡AB的长.(精确到0.1
m)
解:过点B作BE⊥AD于点E,
过点C作CF⊥AD于点F.
在Rt△ABE和Rt△CDF中,
∴AE=3BE=3×23=69(m),FD=2.5CF=2.5×23=57.5(m),
∴AD=AE+EF+FD=69+6+57.5=132.5(m).
∴α≈18.43°.
在Rt△ABE中,由勾股定理,得
AB=
≈72.7(m).
答:斜坡AB的坡角α约为18.43°,坝底宽AD为132.5
m,斜坡AB的长约为72.7
m.
≈0.33,
练
习
1.教材P77练习第1,2题.
2.如图,某办公大楼正前方有一根高度是15
m的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20
m,梯坎坡长BC是12
m,梯坎坡度i=1∶
,则大楼AB的高度约为(精确到0.1
m,参考数据:
≈1.41,
≈1.73,
≈2.45)(
)
A.30.6
m
B.32.1
m
C.37.9
m
D.39.4
m
D
练
习
3.如图,海上有座灯塔P,在它周围3
n
mile有暗礁,一艘客轮以每小时9
n
mile的速度由西向东航行,行至A处测得灯塔P在它的北偏东60°,继续航行10
min后到达B处,又测得灯塔P在它的东北方向.若客轮不改变方向,有无触礁危险?
解:过点P作PD⊥AB于点D.
在Rt△PAD中,∠PAD=30°.
又∵∠PBD=45°,
故设PD=x,则BD=PD=x,AD=x.
∴AD=1.5+x,
∴有触礁危险.
活动5
课堂小结
1.方向角、坡度的概念.
2.掌握与方向角、坡度有关的问题.
四、作业布置与教学反思
1.作业布置
(1)
教材P78习题28.2第5,9题;
2.教学反思
第2课时 与方向角、坡度有关的解直角三角形的应用
一、教学目标
二、教学重难点
重点
难点
1.了解什么是方位角、坡度及方位角的命名特点,准确熟练解决有关方位角问题.
2.巩固用解直角三角形有关知识解决实际问题的方法.
运用解直角三角形解决航行、斜坡问题.
灵活运用解直角三角形的方法解决生活中的实际问题.
活动1
新课导入
三、教学设计
如图,在电线杆的C处拉引线CE,CF固定电线杆.拉线CE和地面成60°角,在离电线杆6
m的B处安置测角仪,在A处测得电线杆上C处的仰角为30°.已知测角仪AB的高为1.5
m,拉线CE的长是__________m.(结果保留根号)
活动2
探究新知
如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80
n
mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(精确到0.01
n
mile)?
65°
34°
P
B
C
A
1.教材P76例5.
解:如图
,在Rt△APC中,
PC=PA·cos(90°-65°)
=80×cos25°
≈80×0.91
=72.8
在Rt△BPC中,∠B=34°
当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130.23n
mile.
65°
34°
P
B
C
A
2.如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6
m,坝高20
m,斜坡AB的坡度i=1∶2.5,斜坡CD的坡角为30°.求坝底AD的长度.(精确到0.1
m,参考数据:
)
答:坝底AD的长度为90.64
m.
≈1.414,
≈1.732
活动3
知识归纳
1.坡度、坡角概念.
如图,BC表示水平面,AB表示坡面,把水平面BC与坡面AB形成的角∠ABC称为坡角α,坡面的铅直高度h与水平宽度l的比叫做坡面的坡度(或坡比),记作i=
=tan
α.
2.利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为________问题(画出平面图形,转化为解直角三角形的问题);
(2)根据问题中的条件,适当选用锐角三角函数等解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
数学
活动4
例题与练习
例1 如图,海中一小岛A,该岛四周10
n
mile内有暗礁,今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20
n
mile后到达该岛的南偏西25°的C处之后,货轮继续向东航行,你认为货轮向东航行的途中会有触礁的危险吗?
解:过点A作AD⊥BC交BC的延长线于点D.
由题意,得∠BAD=55°,∠CAD=25°,BC=20
n
mile.在Rt△ABD中,
∴BD=AD·tan
55°.在Rt△ACD中,
∴CD=AD·tan
25°.
∵BD=BC+CD,
∴AD·tan
55°=20+AD·tan
25°,
答:轮船继续向东行驶,不会有触礁危险.
≈20.79(n
mile)>10(n
mile).
例2 如图,水库大坝的横断面是梯形,坝顶宽6
m,坝高23
m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,求斜坡AB的坡角α,坝底宽AD和斜坡AB的长.(精确到0.1
m)
解:过点B作BE⊥AD于点E,
过点C作CF⊥AD于点F.
在Rt△ABE和Rt△CDF中,
∴AE=3BE=3×23=69(m),FD=2.5CF=2.5×23=57.5(m),
∴AD=AE+EF+FD=69+6+57.5=132.5(m).
∴α≈18.43°.
在Rt△ABE中,由勾股定理,得
AB=
≈72.7(m).
答:斜坡AB的坡角α约为18.43°,坝底宽AD为132.5
m,斜坡AB的长约为72.7
m.
≈0.33,
练
习
1.教材P77练习第1,2题.
2.如图,某办公大楼正前方有一根高度是15
m的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20
m,梯坎坡长BC是12
m,梯坎坡度i=1∶
,则大楼AB的高度约为(精确到0.1
m,参考数据:
≈1.41,
≈1.73,
≈2.45)(
)
A.30.6
m
B.32.1
m
C.37.9
m
D.39.4
m
D
练
习
3.如图,海上有座灯塔P,在它周围3
n
mile有暗礁,一艘客轮以每小时9
n
mile的速度由西向东航行,行至A处测得灯塔P在它的北偏东60°,继续航行10
min后到达B处,又测得灯塔P在它的东北方向.若客轮不改变方向,有无触礁危险?
解:过点P作PD⊥AB于点D.
在Rt△PAD中,∠PAD=30°.
又∵∠PBD=45°,
故设PD=x,则BD=PD=x,AD=x.
∴AD=1.5+x,
∴有触礁危险.
活动5
课堂小结
1.方向角、坡度的概念.
2.掌握与方向角、坡度有关的问题.
四、作业布置与教学反思
1.作业布置
(1)
教材P78习题28.2第5,9题;
2.教学反思
