湖南省岳阳市华容县2020-2021学年高一上学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 湖南省岳阳市华容县2020-2021学年高一上学期期末考试数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 319.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 20:36:45 | ||
图片预览



文档简介
华容县2020-2021学年度第一学期期末考试试卷
高 一 数 学
注意事项:
1、本试卷分选择题和非选择题两部分,共4页。时量100分钟,满分150分。答题前,考生要将自己的姓名、考号填写在答题卡上。
2、回答选择题时,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷和草稿纸上无效。
3、回答非选择题时,用0.5毫米黑色墨水签字笔将答案按题号写在答题卡上。写在本试卷和草稿纸上无效。
4、考试结束时,将答题卡交回。
一、单项选择题(本大题共8小题,每小题5分,满分40分。每小题给出的四个选项中,只有一个选项是符合题目要求的。)
如果集合U={1,2,3,4,5,6,7,8},A={2,4,8},B={1,3,4,7},那么(?UA)∪B等于( )
A. {4} B. {1,3,4,5,6,7} C. {1,3,7} D. (2,8}
命题“false”的否定是( )
A. false B. false
C. false D. false
若函数false,则false
A. lg101 B. 2 C. 1 D. 0
若false,则“false”是“false”的( )
A. 充分条件
B. 必要条件
C. 既不是充分条件也不是必要条件
D. 充要条件
已知函数false(false),则false( )。
A. false B. false
C. false D. false
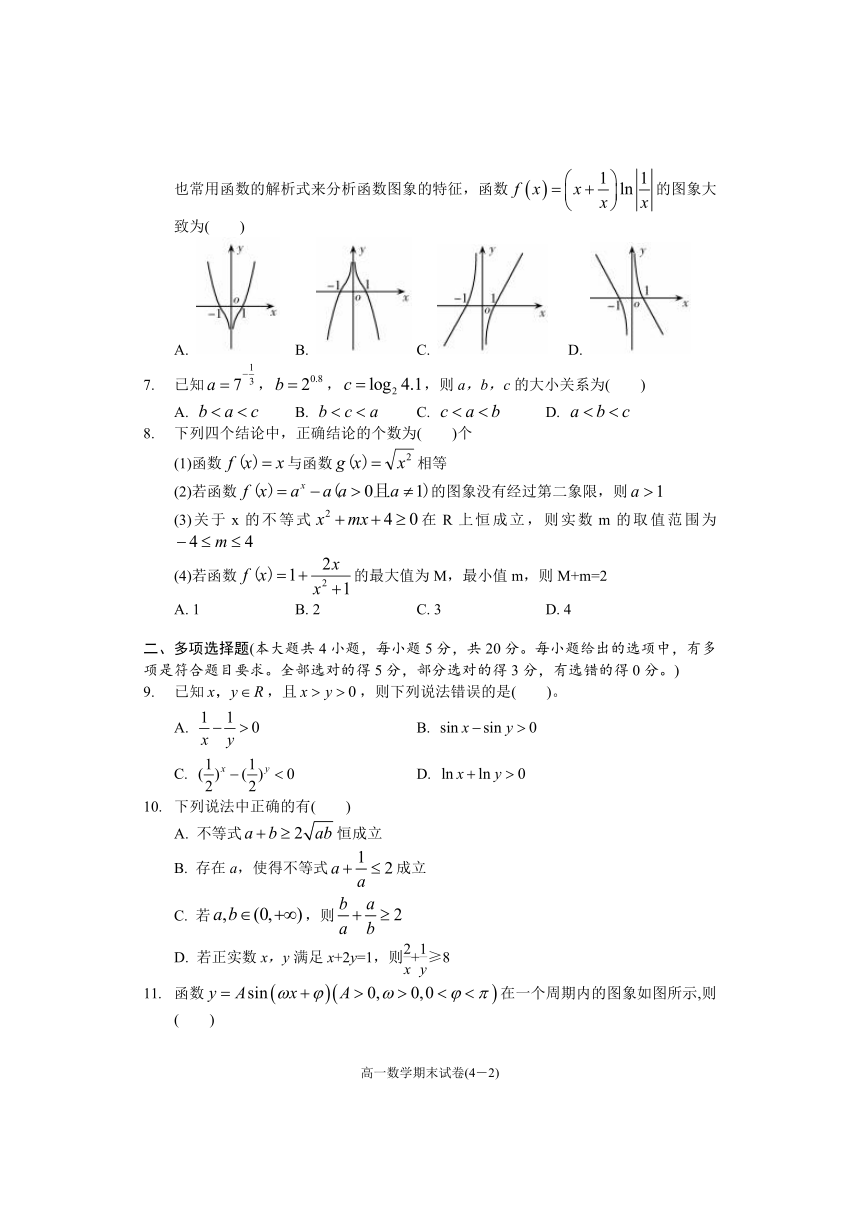
我国著名数学家华罗庚先生曾说:数缺形时少直观,形缺数时难入微数形结合百般好,隔裂分家万事休. 在数学的学习和研究中,常用函数的图象来研究函数的性质,也常用函数的解析式来分析函数图象的特征,函数false的图象大致为( )
A. B. C. D.
已知false,false,false,则a,b,c的大小关系为( )
A. false B. false C. false D. false
下列四个结论中,正确结论的个数为( )个
(1)函数false与函数false相等
(2)若函数false的图象没有经过第二象限,则false
(3)关于x的不等式false在R上恒成立,则实数m的取值范围为false
(4)若函数false的最大值为M,最小值m,则M+m=2
A. 1 B. 2 C. 3 D. 4
二、多项选择题(本大题共4小题,每小题5分,共20分。每小题给出的选项中,有多项是符合题目要求。全部选对的得5分,部分选对的得3分,有选错的得0分。)
已知false,且false,则下列说法错误的是( )。
A. false B. false
C. false D. false
下列说法中正确的有( )
A. 不等式false恒成立
B. 存在a,使得不等式false成立
C. 若false,则false
D. 若正实数x,y满足x+2y=1,则+≥8
函数false在一个周期内的图象如图所示,则( )
336550038735A. 该函数的解析式为false
B. 该函数的对称中心为false
C. 该函数的单调递增区间是false
D. 把函数false的图象上所有点的横坐标变为原来的false,纵坐标不变,可得到该函数图象
设false,用false表示不超过false的最大整数,则false称为高斯函数,也叫取整函数. 令false,以下结论正确的有( )
A. false B. 函数false为奇函数
C. false D. 函数false的值域为false
三、填空题(本大题共4小题,每小题5分,共20分)
若false,则false=_______。
已知函数false的零点位于区间(1,e)内,则实数m的取值范围是________.
函数false(false且false)的图像恒过定点A,若点A在直线mx+ny+2=0上,其中false,false,则false的最小值为________。
已知函数false是定义在R上的奇函数,在区间(﹣∞,0)上单调递增,且false,则满足false的x的取值范围是________________.
四、解答题(本大题共6小题,满分70分。解答应写出文字说明,证明过程或演算步骤)
(本题10分)计算:
(1)false;
(2)已知false,求false.
(本题12分)已知集合falsefalse,false.若“false”是“false”的充分不必要条件,求实数a的取值范围.
(本题12分)已知函数false.
(1)求false的最小正周期;
(2)当false时,
(i)求函数false的单调递减区间;
(ii)求函数false的最大值?最小值,并分别求出使该函数取得最大值?最小值时的自变量x的值.
(本题12分)
定义在R上的函数f(x)满足f(x)= f(x),当x(0,1)时有f(x)=false。
(1)求f(x)在(1,1)上的解析式;
(2)判断f(x)在(0,1)上的单调性并用定义证明。
(本题12分)为了应对“新冠肺炎”我们进行某种药材的人工种植。研究表明:人工种植药材时,某种药材在一定的条件下,每株药材的年平均生长量v(单位:千克)是每平方米种植株数x的函数. 当x不超过4时,v的值为2;当4<x≤20时,v是x的一次函数,其中当x为10时,v的值为4;当x为20时,v的值为0.
(1)当0<x≤20时,求函数v关于x的函数表达式;
(2)当每平方米种植株数x为何值时,每平方米药材的年生长总量(单位:千克)取得最大值?并求出这个最大值. (年生长总量=年平均生长量×种植株数)
(本题12分)数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养.因为运算,数的威力无限;没有运算,数就只是一个符号.对数运算与指数幂运算是两类重要的运算.
(1)对数的运算性质降低了运算的级别,简化了运算,在数学发展史上是伟大的成就.对数运算性质的推导有很多方法.请同学们根据所学知识推导如下的对数运算性质:如果false,且false,false,那么false;
(2)请你运用上述对数运算性质计算false的值;
(3)因为false,所以false的位数为4(一个自然数数位的个数,叫做位数).请你运用所学过的对数运算的知识,判断false的位数.(注false)
华容县2020-2021学年度第一学期期末考试
高一数学参考答案
一、单项选择题(本大题共8小题,每小题5分,满分40分。每小题给出的四个选项中,只有一个选项是符合题目要求的。)
1–5. BCBBC 6–8. DDC
二、多项选择题(本大题共4小题,每小题5分,共20分。每小题给出的选项中,有多是符合题目要求。全部选对的得5分,部分选对的得3分,有选错的得0分。)
9.ABD 10.BCD 11.ACD 12.AD
三、填空题(本大题共4小题,每小题5分,共20分)
13.f(x)=x22x+3 14.(0,1) 15.false 16.(∞, 1]∪[2, +∞)
四、解答题(本大题共6小题,满分70分。解答应写出文字说明,证明过程或演算步骤)
17、解(1)原式false;.............5分
(2)∵false,∴false,
故false..............10分
18、由题意知,A不为空集,false...........+2分
falsefalse,因为“false”是“false”的充分不必要条件,所以A含于B,
则false,等号不同时取到,解得false.
所以实数a的取值范围是false................................12分
19、解:(1)由题意可知:
falsefalse
false.................................+2分
因为false,所以f(x)的最小正周期为.................................+4分
(2)(i)因为false,所以false,
因为false,false的单调递减区间是false,且由false,得false,所以f(x)的单调递减区间为false.................................+8分
(ii)由(ⅰ)可知当false时, f(x)单调递增,当false时, f(x)单调递减,
且false,false,false
所以:当false时, f(x)取最大值为2, 当false时, f(x)取最小值为false.............12分
20、【解析】(1)设false,则false,∵false,且false时,false,.................................................................................................2分
∴false时,有false,....................4分
在false中,令false,falsefalsefalse,...........5分
综上,当false时,有:false;...................6分
(2) f(x)在(0,1)上是减函数,
证明:设false,则false,false,...................8分
∴false,false,
∴false,...........10分
∴f(x2)< f(x1),∴f(x)在(0,1)上是减函数。.......................................................12分
21、解:(1)由题意得,当0<x≤4时,v=2;
当4<x≤20时,设v=ax+b,
由已知得,解得,所以v=﹣x+8,............................2分
故函数v=................................................................6分
(2)设药材每平方米的年生长总量为f(x)千克,
依题意及(1)可得,
当0<x≤4时,f(x)为增函数,故f(x)max=f(4)=4×2=8;
当4<x≤20时,,
此时f(x)max=f(10)=40.
综上所述,可知当每平方米种植10株时,药材的年生长总量取得最大值40千克.......................12分
22、解:(1)方法一:设false,∴false,∴false,
∴false,得证.................................+4分
方法二:设false,∴false,∴false,∴false,
∴false,∴false
方法三:∵false,false,∴false
∴false得证.
(2)方法一:false
falsefalsefalse.................................+8分
方法二:false
falsefalse
falsefalse.
(3)方法一:设false,false,
∴false,∴false,
∴false,∴false
∵false,∴false,∴false的位数为6677................................ 12分
方法二:设false,∴false
∴false,∴false,∴false
∵false,∴N有6677位数,即false的位数为6677
高 一 数 学
注意事项:
1、本试卷分选择题和非选择题两部分,共4页。时量100分钟,满分150分。答题前,考生要将自己的姓名、考号填写在答题卡上。
2、回答选择题时,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷和草稿纸上无效。
3、回答非选择题时,用0.5毫米黑色墨水签字笔将答案按题号写在答题卡上。写在本试卷和草稿纸上无效。
4、考试结束时,将答题卡交回。
一、单项选择题(本大题共8小题,每小题5分,满分40分。每小题给出的四个选项中,只有一个选项是符合题目要求的。)
如果集合U={1,2,3,4,5,6,7,8},A={2,4,8},B={1,3,4,7},那么(?UA)∪B等于( )
A. {4} B. {1,3,4,5,6,7} C. {1,3,7} D. (2,8}
命题“false”的否定是( )
A. false B. false
C. false D. false
若函数false,则false
A. lg101 B. 2 C. 1 D. 0
若false,则“false”是“false”的( )
A. 充分条件
B. 必要条件
C. 既不是充分条件也不是必要条件
D. 充要条件
已知函数false(false),则false( )。
A. false B. false
C. false D. false
我国著名数学家华罗庚先生曾说:数缺形时少直观,形缺数时难入微数形结合百般好,隔裂分家万事休. 在数学的学习和研究中,常用函数的图象来研究函数的性质,也常用函数的解析式来分析函数图象的特征,函数false的图象大致为( )
A. B. C. D.
已知false,false,false,则a,b,c的大小关系为( )
A. false B. false C. false D. false
下列四个结论中,正确结论的个数为( )个
(1)函数false与函数false相等
(2)若函数false的图象没有经过第二象限,则false
(3)关于x的不等式false在R上恒成立,则实数m的取值范围为false
(4)若函数false的最大值为M,最小值m,则M+m=2
A. 1 B. 2 C. 3 D. 4
二、多项选择题(本大题共4小题,每小题5分,共20分。每小题给出的选项中,有多项是符合题目要求。全部选对的得5分,部分选对的得3分,有选错的得0分。)
已知false,且false,则下列说法错误的是( )。
A. false B. false
C. false D. false
下列说法中正确的有( )
A. 不等式false恒成立
B. 存在a,使得不等式false成立
C. 若false,则false
D. 若正实数x,y满足x+2y=1,则+≥8
函数false在一个周期内的图象如图所示,则( )
336550038735A. 该函数的解析式为false
B. 该函数的对称中心为false
C. 该函数的单调递增区间是false
D. 把函数false的图象上所有点的横坐标变为原来的false,纵坐标不变,可得到该函数图象
设false,用false表示不超过false的最大整数,则false称为高斯函数,也叫取整函数. 令false,以下结论正确的有( )
A. false B. 函数false为奇函数
C. false D. 函数false的值域为false
三、填空题(本大题共4小题,每小题5分,共20分)
若false,则false=_______。
已知函数false的零点位于区间(1,e)内,则实数m的取值范围是________.
函数false(false且false)的图像恒过定点A,若点A在直线mx+ny+2=0上,其中false,false,则false的最小值为________。
已知函数false是定义在R上的奇函数,在区间(﹣∞,0)上单调递增,且false,则满足false的x的取值范围是________________.
四、解答题(本大题共6小题,满分70分。解答应写出文字说明,证明过程或演算步骤)
(本题10分)计算:
(1)false;
(2)已知false,求false.
(本题12分)已知集合falsefalse,false.若“false”是“false”的充分不必要条件,求实数a的取值范围.
(本题12分)已知函数false.
(1)求false的最小正周期;
(2)当false时,
(i)求函数false的单调递减区间;
(ii)求函数false的最大值?最小值,并分别求出使该函数取得最大值?最小值时的自变量x的值.
(本题12分)
定义在R上的函数f(x)满足f(x)= f(x),当x(0,1)时有f(x)=false。
(1)求f(x)在(1,1)上的解析式;
(2)判断f(x)在(0,1)上的单调性并用定义证明。
(本题12分)为了应对“新冠肺炎”我们进行某种药材的人工种植。研究表明:人工种植药材时,某种药材在一定的条件下,每株药材的年平均生长量v(单位:千克)是每平方米种植株数x的函数. 当x不超过4时,v的值为2;当4<x≤20时,v是x的一次函数,其中当x为10时,v的值为4;当x为20时,v的值为0.
(1)当0<x≤20时,求函数v关于x的函数表达式;
(2)当每平方米种植株数x为何值时,每平方米药材的年生长总量(单位:千克)取得最大值?并求出这个最大值. (年生长总量=年平均生长量×种植株数)
(本题12分)数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养.因为运算,数的威力无限;没有运算,数就只是一个符号.对数运算与指数幂运算是两类重要的运算.
(1)对数的运算性质降低了运算的级别,简化了运算,在数学发展史上是伟大的成就.对数运算性质的推导有很多方法.请同学们根据所学知识推导如下的对数运算性质:如果false,且false,false,那么false;
(2)请你运用上述对数运算性质计算false的值;
(3)因为false,所以false的位数为4(一个自然数数位的个数,叫做位数).请你运用所学过的对数运算的知识,判断false的位数.(注false)
华容县2020-2021学年度第一学期期末考试
高一数学参考答案
一、单项选择题(本大题共8小题,每小题5分,满分40分。每小题给出的四个选项中,只有一个选项是符合题目要求的。)
1–5. BCBBC 6–8. DDC
二、多项选择题(本大题共4小题,每小题5分,共20分。每小题给出的选项中,有多是符合题目要求。全部选对的得5分,部分选对的得3分,有选错的得0分。)
9.ABD 10.BCD 11.ACD 12.AD
三、填空题(本大题共4小题,每小题5分,共20分)
13.f(x)=x22x+3 14.(0,1) 15.false 16.(∞, 1]∪[2, +∞)
四、解答题(本大题共6小题,满分70分。解答应写出文字说明,证明过程或演算步骤)
17、解(1)原式false;.............5分
(2)∵false,∴false,
故false..............10分
18、由题意知,A不为空集,false...........+2分
falsefalse,因为“false”是“false”的充分不必要条件,所以A含于B,
则false,等号不同时取到,解得false.
所以实数a的取值范围是false................................12分
19、解:(1)由题意可知:
falsefalse
false.................................+2分
因为false,所以f(x)的最小正周期为.................................+4分
(2)(i)因为false,所以false,
因为false,false的单调递减区间是false,且由false,得false,所以f(x)的单调递减区间为false.................................+8分
(ii)由(ⅰ)可知当false时, f(x)单调递增,当false时, f(x)单调递减,
且false,false,false
所以:当false时, f(x)取最大值为2, 当false时, f(x)取最小值为false.............12分
20、【解析】(1)设false,则false,∵false,且false时,false,.................................................................................................2分
∴false时,有false,....................4分
在false中,令false,falsefalsefalse,...........5分
综上,当false时,有:false;...................6分
(2) f(x)在(0,1)上是减函数,
证明:设false,则false,false,...................8分
∴false,false,
∴false,...........10分
∴f(x2)< f(x1),∴f(x)在(0,1)上是减函数。.......................................................12分
21、解:(1)由题意得,当0<x≤4时,v=2;
当4<x≤20时,设v=ax+b,
由已知得,解得,所以v=﹣x+8,............................2分
故函数v=................................................................6分
(2)设药材每平方米的年生长总量为f(x)千克,
依题意及(1)可得,
当0<x≤4时,f(x)为增函数,故f(x)max=f(4)=4×2=8;
当4<x≤20时,,
此时f(x)max=f(10)=40.
综上所述,可知当每平方米种植10株时,药材的年生长总量取得最大值40千克.......................12分
22、解:(1)方法一:设false,∴false,∴false,
∴false,得证.................................+4分
方法二:设false,∴false,∴false,∴false,
∴false,∴false
方法三:∵false,false,∴false
∴false得证.
(2)方法一:false
falsefalsefalse.................................+8分
方法二:false
falsefalse
falsefalse.
(3)方法一:设false,false,
∴false,∴false,
∴false,∴false
∵false,∴false,∴false的位数为6677................................ 12分
方法二:设false,∴false
∴false,∴false,∴false
∵false,∴N有6677位数,即false的位数为6677
同课章节目录
