四年级数学下册课件-6.3 整数加法运算定律推广到小数人教版 52页
文档属性
| 名称 | 四年级数学下册课件-6.3 整数加法运算定律推广到小数人教版 52页 |  | |
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 20:42:12 | ||
图片预览







文档简介
(共52张PPT)
整数加法运算定律推广到小数
脱式计算:
47+26+74=
135+39+65+11=
134-66-34=
我先考验一下你们的计算能力。
47+26+74
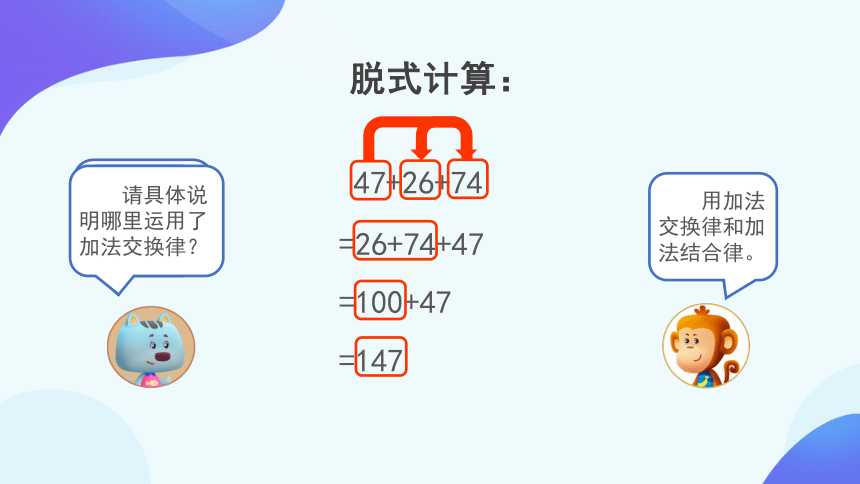
脱式计算:
=26+74+47
=100+47
=147
这道题用什么样的方法快速算出答案?
简便算法。
用加法交换律和加法结合律。
怎样简便的算法?
请具体说明哪里运用了加法交换律?
脱式计算:
47+26+74
=26+74+47
=100+47
=147
这道题用什么样的方法快速算出答案?
加法交换律。
加法交换律的内容是什么?
两个数相加,交换加数的位置,和不变。
如果用字母怎样表示?
a+b=b+a
用加法交换律和加法结合律。
脱式计算:
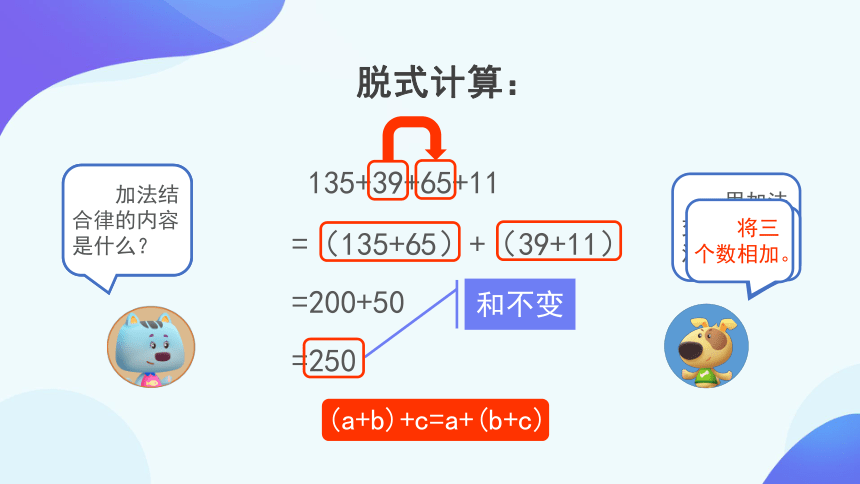
135+39+65+11
=(135+65)+(39+11)
=200+50
=250
这道题用什么样的方法快速算出答案?
加法结合律。
将三个数相加。
和不变
(a+b)+c=a+(b+c)
加法结合律的内容是什么?
脱式计算:
134-66-34
=134-(66+34)
=134-100
=34
这道题用什么样的方法快速算出答案?
利用了减法的性质。
减法的性质具体内容是什么?
一个数连续减去两个数,可以用这个数减去两个数的和。
如果用字母怎样表示?
a-b-c=a-(b+c)
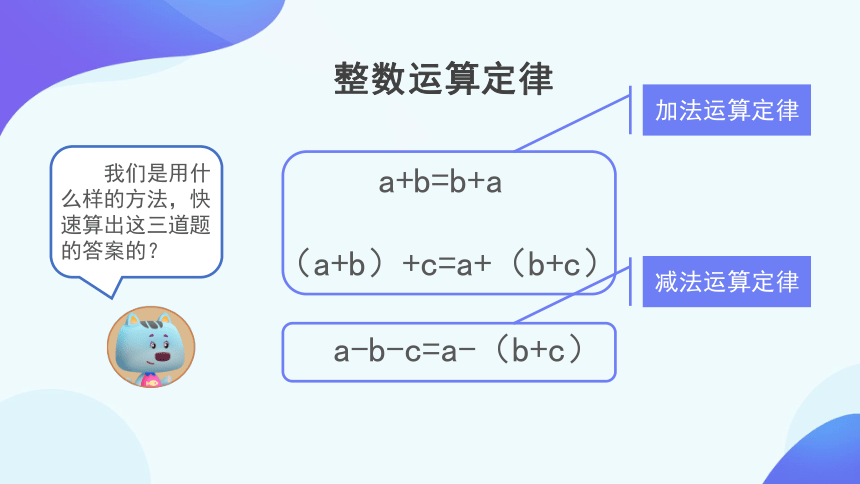
整数运算定律
a+b=b+a
(a+b)+c=a+(b+c)
a-b-c=a-(b+c)
我们是用什么样的方法,快速算出这三道题的答案的?
加法运算定律
减法运算定律
表示整数
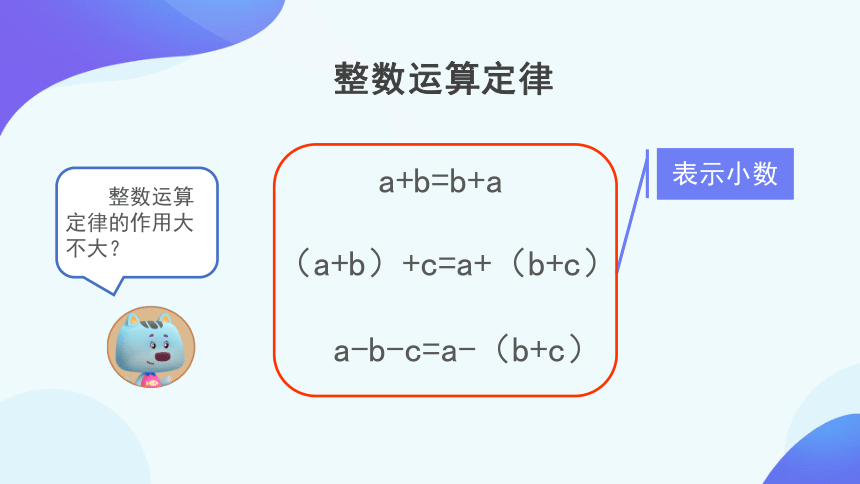
整数运算定律
a+b=b+a
(a+b)+c=a+(b+c)
a-b-c=a-(b+c)
整数运算定律的作用大不大?
表示小数
整数运算定律
猜想
整数的运算定律,能够运用到小数当中吗?
验证
(举例)
举例验证
a+b=b+a
能不能用举例的方法,验证小数当中是否可以使用加法交换率呢?
举例验证
1.2+3.5
3.5+1.2
计算结果,看得数是否相等
举例验证
1.2+3.5
3.5+1.2
=
4.7
4.7
=
同学们,请在自己的课堂本上列举两组这样的例子。
举例验证
1.5+2.5
2.5+1.5
=
4
4
=
计算
举例验证
3.7+4.3
4.3+3.7
=
8
8
=
举例验证
7.3+7.4
7.4+7.3
=
14.7
14.7
=
举例验证
4.7+2.6
2.6+4.7
=
7.3
7.3
=
举例验证
3.4+2.6
2.6+3.4
=
6
6
=
举例验证
4.5+5.4
4.5+5.4
=
9.9
9.9
=
整数运算定律
a+b=b+a
(a+b)+c=a+(b+c)
a-b-c=a-(b+c)
我们可以用哪一个等式表示这类例子?
整数的加法交换律,能运用到小数当中吗?
整数运算定律
猜想
验证(举例)
结论
我们就可以得出一个什么?
同学们,我们进行了猜想,而且进行了举例,验证说明整数的加法交换律,同样可以应用到小数中。
举例验证
整数的加法结合律,能运用到小数当中吗?
(a+b)+c=a+(b+c)
猜想
验证(举例)
举例验证
(3.4+1.5)+2.5
3.4+(1.5+2.5)
=
4.9
4
验算。
7.4
7.4
小数也能运用结合律
你得到一个什么结论?
小数也能运用加法结合律
举例验证
(3.4+1.5)+2.5
3.4+(1.5+2.5)
=
4.9
4
你选择哪边的算法,为什么?
7.4
7.4
凑成整数
计算整数比小数简便
举例验证
整数的减法的运算性质,能运用到小数当中吗?
a-b-c=a-(b+c)
a-b-c=a-(b+c)
举例验证
340-25.4-74.6
340-(25.4+74.6)
=
100
这道题应该等于什么?
计算整数比小数简便
知识小结
猜想
验证(举例)
结论
我们得出了一个什么结论?请你概括一下。
我们得出了小数也能运用整数的运算定律的结论。
整数的运算定律,小数也可以适用。
整数运算定律
a+b=b+a
(a+b)+c=a+(b+c)
a-b-c=a-(b+c)
整数的运算定律,可以推广到什么当中?
推广到小数
只代表整数?
代表小数
同学们,只要我们敢大胆猜想,就能得到伟大的什么?
结论。
只要同学们敢大胆猜想,然后举例验证,就能够得到伟大的结论。
下面每组算式两边的结果相等吗?
3.2+0.5
0.5+3.2
=
=
(4.7+2.6)+7.4
4.7+(2.6+7.4)
整数加法的交换律、结合律对小数加法同样适用
应用运算定律,可以使一些小数计算更简便
加法交换律
加法结合律
计算0.6+7.91+3.4+0.09。
0.6+7.91+3.4+0.09
=8.51+3.4+0.09
=11.91+0.09
=12
我这样算。
我这样算。
小丽
小伟
0.6+7.91+3.4+0.09
=(0.6+3.4)+(7.91+0.09)
=4+8
=12
计算0.6+7.91+3.4+0.09。
0.6+7.91+3.4+0.09
=8.51+3.4+0.09
=11.91+0.09
=12
我这样算。
我这样算。
小丽
小伟
0.6+7.91+3.4+0.09
=(0.6+3.4)+(7.91+0.09)
=4+8
=12
×
√
计算0.6+7.91+3.4+0.09。
0.6+7.91+3.4+0.09
=8.51+3.4+0.09
=11.91+0.09
=12
我这样算。
我这样算。
小丽
小伟
0.6+7.91+3.4+0.09
=(0.6+3.4)+(7.91+0.09)
=4+8
=12
顺序计算
简便计算
加法交换律和加法结合律
计算简便
凑成整数
×
√
(1)6.7+4.95+3.3=6.7+
+4.95
(2)(1.38+1.75)+0.25=
+(
+
)
在
里填上适当的数。
3.3
加法结合律和加法交换律
(1)6.7+4.95+3.3=6.7+
+4.95
(2)(1.38+1.75)+0.25=
+(
+
)
在
里填上适当的数。
3.3
(1)6.7+4.95+3.3=6.7+
+4.95
(2)(1.38+1.75)+0.25=
+(
+
)
在
里填上适当的数。
3.3
1.38
1.75
0.25
加法结合律
1.88+2.3+3.7
计算下面各题,怎样简便就怎么计算。
4.02-3.5+0.98
5.17-1.8-3.2
13.7+0.98+0.02+4.3
=1.88+(2.3+3.7)
=1.88+6
=7.88
计算下面各题,怎样简便就怎么计算。
为什么在这里加一个括号?
凑成整数
1.88+2.3+3.7
√
=4.02+0.98-3.5
=5-3.5
=1.5
计算下面各题,怎样简便就怎么计算。
为什么减号和加号可以互相换位置?
凑成整数
4.02-3.5+0.98
加法和减法同级
计算结果不变
=4.02+0.98-3.5
=5-3.5
=1.5
计算下面各题,怎样简便就怎么计算。
这道题运用的是什么运算定律?
4.02-3.5+0.98
a+b=b+a
减号
符号不变
带着符号一起交换。
√
=5.17-(1.8+3.2)
=5.17-5
=0.17
计算下面各题,怎样简便就怎么计算。
减法的性质
√
5.17-1.8-3.2
=(13.7+4.3)+(0.98+0.02)
=18+0.1
=18.1
计算下面各题,怎样简便就怎么计算。
√
凑整,或者使小数计算更简便。
13.7+0.98+0.02+4.3
凑成整数
同学们,通过这节课的学习,你学会了什么?说一说你的收获。
我学会了整数的运算定律可以推广到小数。
我们还可以猜想,乘法和除法的定律可以推广到小数。
除了加法和减法的运算定律可以推广到小数,你还可以猜想什么?
任何的运算定律都可以推算到小数。
运算定律中的字母,只能代表整数和小数吗?猜想一下,还可以怎么样?
不仅可以代表整数和小数,还可以代表分数。
16.5+37.1+(
)+
(
)
24.6+1.93+(
)+
(
)
200-48.8-(
)
通过今天的学习,让你当当小老师,给同学们出出题,敢接受挑战吗?
要求:能进行简便计算。
共同点
16.5+37.1+(
)+
(
)
16.5+37.1+(
)+
(
)
16.5+37.1+(
)+
(
)
16.5+37.1+(
)+
(
)
通过今天的学习,让你当当小老师,给同学们出出题,敢接受挑战吗?
13.5
32.9
3.5
2.9
62.9
3.5
23.5
62.9
5和9
为了凑整
出题的时候,第一步应该注意什么?
注意小数的凑整。
让小数怎么样?
让小数进位。
小数怎么样才能进位?
凑整。
24.6+1.93+(
)+
(
)
通过今天的学习,让你当当小老师,给同学们出出题,敢接受挑战吗?
4
7
×
07
7加9进位,无法凑整
同学们,你们在学习这节课之后,不仅学会了怎么解决问题,而且还学会了怎么出题。
你真棒!
再见!
整数加法运算定律推广到小数
脱式计算:
47+26+74=
135+39+65+11=
134-66-34=
我先考验一下你们的计算能力。
47+26+74
脱式计算:
=26+74+47
=100+47
=147
这道题用什么样的方法快速算出答案?
简便算法。
用加法交换律和加法结合律。
怎样简便的算法?
请具体说明哪里运用了加法交换律?
脱式计算:
47+26+74
=26+74+47
=100+47
=147
这道题用什么样的方法快速算出答案?
加法交换律。
加法交换律的内容是什么?
两个数相加,交换加数的位置,和不变。
如果用字母怎样表示?
a+b=b+a
用加法交换律和加法结合律。
脱式计算:
135+39+65+11
=(135+65)+(39+11)
=200+50
=250
这道题用什么样的方法快速算出答案?
加法结合律。
将三个数相加。
和不变
(a+b)+c=a+(b+c)
加法结合律的内容是什么?
脱式计算:
134-66-34
=134-(66+34)
=134-100
=34
这道题用什么样的方法快速算出答案?
利用了减法的性质。
减法的性质具体内容是什么?
一个数连续减去两个数,可以用这个数减去两个数的和。
如果用字母怎样表示?
a-b-c=a-(b+c)
整数运算定律
a+b=b+a
(a+b)+c=a+(b+c)
a-b-c=a-(b+c)
我们是用什么样的方法,快速算出这三道题的答案的?
加法运算定律
减法运算定律
表示整数
整数运算定律
a+b=b+a
(a+b)+c=a+(b+c)
a-b-c=a-(b+c)
整数运算定律的作用大不大?
表示小数
整数运算定律
猜想
整数的运算定律,能够运用到小数当中吗?
验证
(举例)
举例验证
a+b=b+a
能不能用举例的方法,验证小数当中是否可以使用加法交换率呢?
举例验证
1.2+3.5
3.5+1.2
计算结果,看得数是否相等
举例验证
1.2+3.5
3.5+1.2
=
4.7
4.7
=
同学们,请在自己的课堂本上列举两组这样的例子。
举例验证
1.5+2.5
2.5+1.5
=
4
4
=
计算
举例验证
3.7+4.3
4.3+3.7
=
8
8
=
举例验证
7.3+7.4
7.4+7.3
=
14.7
14.7
=
举例验证
4.7+2.6
2.6+4.7
=
7.3
7.3
=
举例验证
3.4+2.6
2.6+3.4
=
6
6
=
举例验证
4.5+5.4
4.5+5.4
=
9.9
9.9
=
整数运算定律
a+b=b+a
(a+b)+c=a+(b+c)
a-b-c=a-(b+c)
我们可以用哪一个等式表示这类例子?
整数的加法交换律,能运用到小数当中吗?
整数运算定律
猜想
验证(举例)
结论
我们就可以得出一个什么?
同学们,我们进行了猜想,而且进行了举例,验证说明整数的加法交换律,同样可以应用到小数中。
举例验证
整数的加法结合律,能运用到小数当中吗?
(a+b)+c=a+(b+c)
猜想
验证(举例)
举例验证
(3.4+1.5)+2.5
3.4+(1.5+2.5)
=
4.9
4
验算。
7.4
7.4
小数也能运用结合律
你得到一个什么结论?
小数也能运用加法结合律
举例验证
(3.4+1.5)+2.5
3.4+(1.5+2.5)
=
4.9
4
你选择哪边的算法,为什么?
7.4
7.4
凑成整数
计算整数比小数简便
举例验证
整数的减法的运算性质,能运用到小数当中吗?
a-b-c=a-(b+c)
a-b-c=a-(b+c)
举例验证
340-25.4-74.6
340-(25.4+74.6)
=
100
这道题应该等于什么?
计算整数比小数简便
知识小结
猜想
验证(举例)
结论
我们得出了一个什么结论?请你概括一下。
我们得出了小数也能运用整数的运算定律的结论。
整数的运算定律,小数也可以适用。
整数运算定律
a+b=b+a
(a+b)+c=a+(b+c)
a-b-c=a-(b+c)
整数的运算定律,可以推广到什么当中?
推广到小数
只代表整数?
代表小数
同学们,只要我们敢大胆猜想,就能得到伟大的什么?
结论。
只要同学们敢大胆猜想,然后举例验证,就能够得到伟大的结论。
下面每组算式两边的结果相等吗?
3.2+0.5
0.5+3.2
=
=
(4.7+2.6)+7.4
4.7+(2.6+7.4)
整数加法的交换律、结合律对小数加法同样适用
应用运算定律,可以使一些小数计算更简便
加法交换律
加法结合律
计算0.6+7.91+3.4+0.09。
0.6+7.91+3.4+0.09
=8.51+3.4+0.09
=11.91+0.09
=12
我这样算。
我这样算。
小丽
小伟
0.6+7.91+3.4+0.09
=(0.6+3.4)+(7.91+0.09)
=4+8
=12
计算0.6+7.91+3.4+0.09。
0.6+7.91+3.4+0.09
=8.51+3.4+0.09
=11.91+0.09
=12
我这样算。
我这样算。
小丽
小伟
0.6+7.91+3.4+0.09
=(0.6+3.4)+(7.91+0.09)
=4+8
=12
×
√
计算0.6+7.91+3.4+0.09。
0.6+7.91+3.4+0.09
=8.51+3.4+0.09
=11.91+0.09
=12
我这样算。
我这样算。
小丽
小伟
0.6+7.91+3.4+0.09
=(0.6+3.4)+(7.91+0.09)
=4+8
=12
顺序计算
简便计算
加法交换律和加法结合律
计算简便
凑成整数
×
√
(1)6.7+4.95+3.3=6.7+
+4.95
(2)(1.38+1.75)+0.25=
+(
+
)
在
里填上适当的数。
3.3
加法结合律和加法交换律
(1)6.7+4.95+3.3=6.7+
+4.95
(2)(1.38+1.75)+0.25=
+(
+
)
在
里填上适当的数。
3.3
(1)6.7+4.95+3.3=6.7+
+4.95
(2)(1.38+1.75)+0.25=
+(
+
)
在
里填上适当的数。
3.3
1.38
1.75
0.25
加法结合律
1.88+2.3+3.7
计算下面各题,怎样简便就怎么计算。
4.02-3.5+0.98
5.17-1.8-3.2
13.7+0.98+0.02+4.3
=1.88+(2.3+3.7)
=1.88+6
=7.88
计算下面各题,怎样简便就怎么计算。
为什么在这里加一个括号?
凑成整数
1.88+2.3+3.7
√
=4.02+0.98-3.5
=5-3.5
=1.5
计算下面各题,怎样简便就怎么计算。
为什么减号和加号可以互相换位置?
凑成整数
4.02-3.5+0.98
加法和减法同级
计算结果不变
=4.02+0.98-3.5
=5-3.5
=1.5
计算下面各题,怎样简便就怎么计算。
这道题运用的是什么运算定律?
4.02-3.5+0.98
a+b=b+a
减号
符号不变
带着符号一起交换。
√
=5.17-(1.8+3.2)
=5.17-5
=0.17
计算下面各题,怎样简便就怎么计算。
减法的性质
√
5.17-1.8-3.2
=(13.7+4.3)+(0.98+0.02)
=18+0.1
=18.1
计算下面各题,怎样简便就怎么计算。
√
凑整,或者使小数计算更简便。
13.7+0.98+0.02+4.3
凑成整数
同学们,通过这节课的学习,你学会了什么?说一说你的收获。
我学会了整数的运算定律可以推广到小数。
我们还可以猜想,乘法和除法的定律可以推广到小数。
除了加法和减法的运算定律可以推广到小数,你还可以猜想什么?
任何的运算定律都可以推算到小数。
运算定律中的字母,只能代表整数和小数吗?猜想一下,还可以怎么样?
不仅可以代表整数和小数,还可以代表分数。
16.5+37.1+(
)+
(
)
24.6+1.93+(
)+
(
)
200-48.8-(
)
通过今天的学习,让你当当小老师,给同学们出出题,敢接受挑战吗?
要求:能进行简便计算。
共同点
16.5+37.1+(
)+
(
)
16.5+37.1+(
)+
(
)
16.5+37.1+(
)+
(
)
16.5+37.1+(
)+
(
)
通过今天的学习,让你当当小老师,给同学们出出题,敢接受挑战吗?
13.5
32.9
3.5
2.9
62.9
3.5
23.5
62.9
5和9
为了凑整
出题的时候,第一步应该注意什么?
注意小数的凑整。
让小数怎么样?
让小数进位。
小数怎么样才能进位?
凑整。
24.6+1.93+(
)+
(
)
通过今天的学习,让你当当小老师,给同学们出出题,敢接受挑战吗?
4
7
×
07
7加9进位,无法凑整
同学们,你们在学习这节课之后,不仅学会了怎么解决问题,而且还学会了怎么出题。
你真棒!
再见!
