2020-2021学年人教版数学八年级下册18.1.1平行四边形性质课件(共17张ppt)
文档属性
| 名称 | 2020-2021学年人教版数学八年级下册18.1.1平行四边形性质课件(共17张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 410.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 16:17:11 | ||
图片预览




文档简介
(共17张PPT)
八年级上册(RJ)
18.1平行四边形性质
自主学习反馈
完成率反馈,表扬优秀学生;由平台数据,找到共性和个性问题。
表扬:课前检测正确率高的学生:图片展示
学案书写工整的学生:图片展示(主要是学案上主观题书写规范展示)
课前检测和学案整体完成情况较好的学生:图片展示(课前自主学习整体完成优秀展示)
问题:共性典型问题:图片展示(课前自主学习中两个或者至多三个典型共性问题的展示)
个性典型问题:图片展示(课前自主学习中两个或者至多三个典型个性问题的展示)
学习目标
(1)掌握平行四边形对角线互相平分的性质.
(2)经历对平行四边形性质的猜想与证明的过程,渗透转化思想,体会图形性质探究的一般思路.
(3)体会几何研究的一般思路与方法.
自学释疑、拓展提升
知识点一:平行四边形对角线的性质
自学问题:灵活利用平行四边形对角线性质进行基本的计算或证明;学会分别从题设或结论出发寻求论证思路的方法.
学生典型问题展示:《平行四边形的性质课前自测》中第1、2、3题的正确率,以及做错的学生的错题选项;教材中44页练习1、2做错学生的错题内容.
自学释疑、拓展提升
知识点一:平行四边形对角线的性质
问题解决:
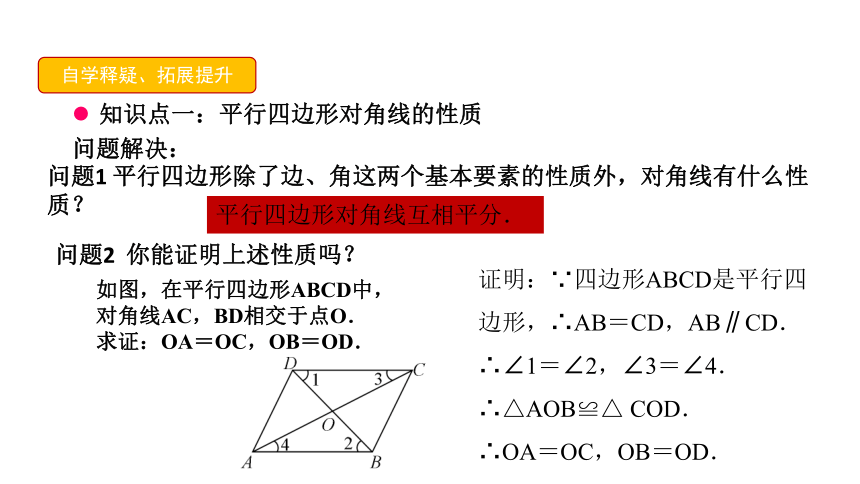
如图,在平行四边形ABCD中,对角线AC,BD相交于点O.
求证:OA=OC,OB=OD.
问题1
平行四边形除了边、角这两个基本要素的性质外,对角线有什么性质?
平行四边形对角线互相平分.
问题2
你能证明上述性质吗?
证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD.
∴∠1=∠2,∠3=∠4.
∴△AOB≌△
COD.
∴OA=OC,OB=OD.
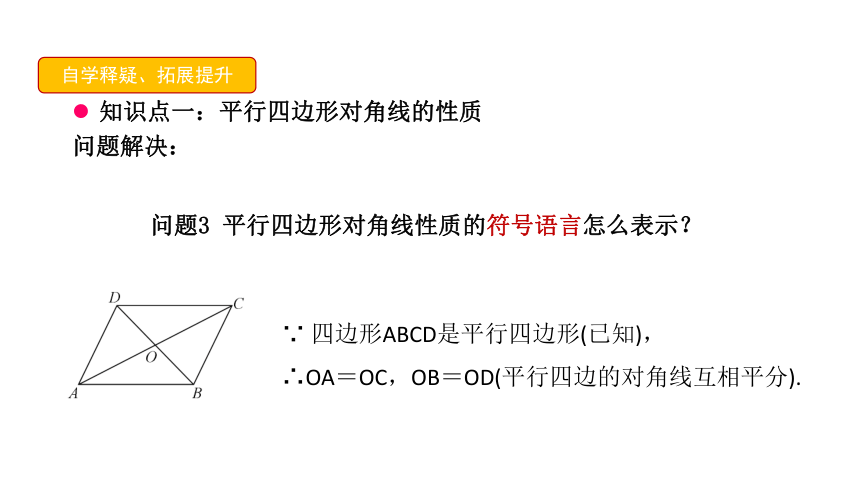
∵
四边形ABCD是平行四边形(已知),
∴OA=OC,OB=OD(平行四边的对角线互相平分).
自学释疑、拓展提升
知识点一:平行四边形对角线的性质
问题解决:
问题3
平行四边形对角线性质的符号语言怎么表示?
自学释疑、拓展提升
知识点一:平行四边形对角线的性质
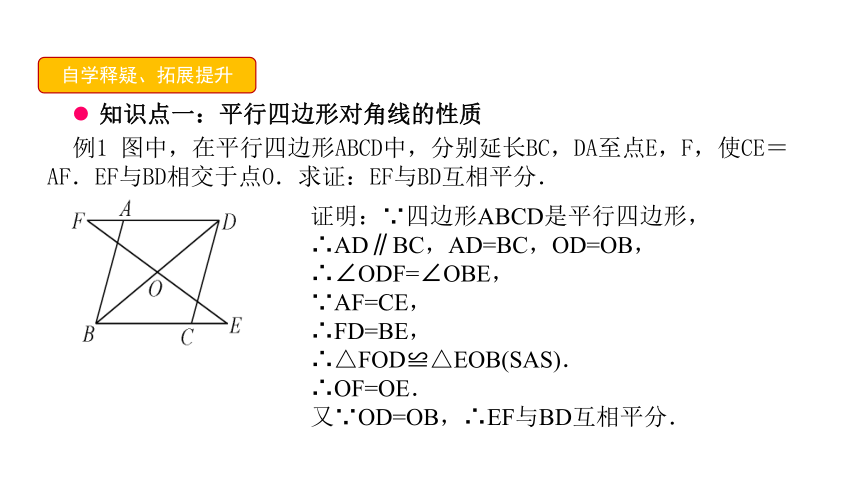
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,OD=OB,∴∠ODF=∠OBE,
∵AF=CE,
∴FD=BE,
∴△FOD≌△EOB(SAS).
∴OF=OE.
又∵OD=OB,∴EF与BD互相平分.
例1
图中,在平行四边形ABCD中,分别延长BC,DA至点E,F,使CE=AF.EF与BD相交于点O.求证:EF与BD互相平分.
同类题检测:平板推题
已知:如图,E,F是平行四边形ABCD的对角线AC上的两点,
AE=CF.求证:EB∥DF.
自学释疑、拓展提升
知识点二:?平行四边形的面积问题
自学问题:不能灵活运用关于平行四边形面积问题得出的结论.
学生典型问题展示:《平行四边形的性质课前自测》中第4、5题的正确率以及做错的学生的错题选项.
自学释疑、拓展提升
知识点二:平行四边形的面积问题
问题解决:
如图,在?ABCD中,AE⊥BC于E,AF⊥CD于F,
则S?ABCD=BC·AE=CD·AF.
问题
平行四边形的面积公式是什么?
平行四边形的面积=底×高.
自学释疑、拓展提升
知识点二:平行四边形的面积问题
问题解决:
情境:一位饱经苍桑的老人,经过一辈子的辛勤劳动,到晚年的时候,终于拥有了一块平行四边形的土地.由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的(如图):
如何判断分得的三角形面积相等?
总结:?ABCD的对角线AC,BD相交于点O,
则S△AOB=S△BOC=S△COD=S△DOA=
S?ABCD.
自学释疑、拓展提升
知识点二:平行四边形的面积问题
问题解决:
例2
(1)如图,?ABCD的对角线AC和BD相交于点O,
与△OBC面积相等的三角形(不包括自身)的个数是(
)
A.4
B.3
C.2
D.1
(2)已知在?ABCD中,AC,BD交于点O,△AOB的面积为2,那么?ABCD的面积为
.
自学释疑、拓展提升
知识点二:平行四边形的面积问题
问题解决:
例3
如图,在?ABCD中,对角线AC,BD交于点O,过点O作直线EF,交AD,BC于点E,F.
(1)求证:OE=OF;
(2)四边形ABFE的面积与四边形FCDE的面积间有何关系?
解:(1)证明:∵四边形ABCD是平行四边形,
∴AO=OC,AD∥BC.∴∠EAO=∠FCO.
在△AOE和△COF中,∴△AOE≌△COF(ASA).∴OE=OF.
(2)S四边形ABFE=S四边形FCDE.理由如下:
∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,∠ABC=∠CDA.
∴△ABC≌△CDA(SAS).∴S△ABC=S△CDA.
由(1)可知△AOE≌△COF,∴S△AOE=S△COF.
又∵S四边形ABFE=S△ABC+S△AOE-S△COF,
S四边形FCDE=S△CDA+S△COF-S△AOE,
∴S四边形ABFE=S四边形FCDE.
同类题检测:平板推题
1.如图,在?ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为
.
2.如图所示,平行四边形ABCD中,对角线AC,BD相交于点O,过点O的直线与AD,BC分别交于点M,N.
(1)若四边形ABNM的面积为4,则平行四边形ABCD的面积为________;
(2)若△CON的面积为2,△DOM的面积为4,则平行四边形ABCD的面积为________.
课堂总结
(1)说说平行四边形有哪些性质?
(2)结合本节课的学习,谈谈研究平行四边形性质的思想方法.
(3)你对平行四边形的面积问题有哪些认识?
课堂总结
1
2
3
积
分
榜
八年级上册(RJ)
18.1平行四边形性质
自主学习反馈
完成率反馈,表扬优秀学生;由平台数据,找到共性和个性问题。
表扬:课前检测正确率高的学生:图片展示
学案书写工整的学生:图片展示(主要是学案上主观题书写规范展示)
课前检测和学案整体完成情况较好的学生:图片展示(课前自主学习整体完成优秀展示)
问题:共性典型问题:图片展示(课前自主学习中两个或者至多三个典型共性问题的展示)
个性典型问题:图片展示(课前自主学习中两个或者至多三个典型个性问题的展示)
学习目标
(1)掌握平行四边形对角线互相平分的性质.
(2)经历对平行四边形性质的猜想与证明的过程,渗透转化思想,体会图形性质探究的一般思路.
(3)体会几何研究的一般思路与方法.
自学释疑、拓展提升
知识点一:平行四边形对角线的性质
自学问题:灵活利用平行四边形对角线性质进行基本的计算或证明;学会分别从题设或结论出发寻求论证思路的方法.
学生典型问题展示:《平行四边形的性质课前自测》中第1、2、3题的正确率,以及做错的学生的错题选项;教材中44页练习1、2做错学生的错题内容.
自学释疑、拓展提升
知识点一:平行四边形对角线的性质
问题解决:
如图,在平行四边形ABCD中,对角线AC,BD相交于点O.
求证:OA=OC,OB=OD.
问题1
平行四边形除了边、角这两个基本要素的性质外,对角线有什么性质?
平行四边形对角线互相平分.
问题2
你能证明上述性质吗?
证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD.
∴∠1=∠2,∠3=∠4.
∴△AOB≌△
COD.
∴OA=OC,OB=OD.
∵
四边形ABCD是平行四边形(已知),
∴OA=OC,OB=OD(平行四边的对角线互相平分).
自学释疑、拓展提升
知识点一:平行四边形对角线的性质
问题解决:
问题3
平行四边形对角线性质的符号语言怎么表示?
自学释疑、拓展提升
知识点一:平行四边形对角线的性质
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,OD=OB,∴∠ODF=∠OBE,
∵AF=CE,
∴FD=BE,
∴△FOD≌△EOB(SAS).
∴OF=OE.
又∵OD=OB,∴EF与BD互相平分.
例1
图中,在平行四边形ABCD中,分别延长BC,DA至点E,F,使CE=AF.EF与BD相交于点O.求证:EF与BD互相平分.
同类题检测:平板推题
已知:如图,E,F是平行四边形ABCD的对角线AC上的两点,
AE=CF.求证:EB∥DF.
自学释疑、拓展提升
知识点二:?平行四边形的面积问题
自学问题:不能灵活运用关于平行四边形面积问题得出的结论.
学生典型问题展示:《平行四边形的性质课前自测》中第4、5题的正确率以及做错的学生的错题选项.
自学释疑、拓展提升
知识点二:平行四边形的面积问题
问题解决:
如图,在?ABCD中,AE⊥BC于E,AF⊥CD于F,
则S?ABCD=BC·AE=CD·AF.
问题
平行四边形的面积公式是什么?
平行四边形的面积=底×高.
自学释疑、拓展提升
知识点二:平行四边形的面积问题
问题解决:
情境:一位饱经苍桑的老人,经过一辈子的辛勤劳动,到晚年的时候,终于拥有了一块平行四边形的土地.由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的(如图):
如何判断分得的三角形面积相等?
总结:?ABCD的对角线AC,BD相交于点O,
则S△AOB=S△BOC=S△COD=S△DOA=
S?ABCD.
自学释疑、拓展提升
知识点二:平行四边形的面积问题
问题解决:
例2
(1)如图,?ABCD的对角线AC和BD相交于点O,
与△OBC面积相等的三角形(不包括自身)的个数是(
)
A.4
B.3
C.2
D.1
(2)已知在?ABCD中,AC,BD交于点O,△AOB的面积为2,那么?ABCD的面积为
.
自学释疑、拓展提升
知识点二:平行四边形的面积问题
问题解决:
例3
如图,在?ABCD中,对角线AC,BD交于点O,过点O作直线EF,交AD,BC于点E,F.
(1)求证:OE=OF;
(2)四边形ABFE的面积与四边形FCDE的面积间有何关系?
解:(1)证明:∵四边形ABCD是平行四边形,
∴AO=OC,AD∥BC.∴∠EAO=∠FCO.
在△AOE和△COF中,∴△AOE≌△COF(ASA).∴OE=OF.
(2)S四边形ABFE=S四边形FCDE.理由如下:
∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,∠ABC=∠CDA.
∴△ABC≌△CDA(SAS).∴S△ABC=S△CDA.
由(1)可知△AOE≌△COF,∴S△AOE=S△COF.
又∵S四边形ABFE=S△ABC+S△AOE-S△COF,
S四边形FCDE=S△CDA+S△COF-S△AOE,
∴S四边形ABFE=S四边形FCDE.
同类题检测:平板推题
1.如图,在?ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为
.
2.如图所示,平行四边形ABCD中,对角线AC,BD相交于点O,过点O的直线与AD,BC分别交于点M,N.
(1)若四边形ABNM的面积为4,则平行四边形ABCD的面积为________;
(2)若△CON的面积为2,△DOM的面积为4,则平行四边形ABCD的面积为________.
课堂总结
(1)说说平行四边形有哪些性质?
(2)结合本节课的学习,谈谈研究平行四边形性质的思想方法.
(3)你对平行四边形的面积问题有哪些认识?
课堂总结
1
2
3
积
分
榜
