六年级下册数学—圆柱表面积培优训练(含答案)
文档属性
| 名称 | 六年级下册数学—圆柱表面积培优训练(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 709.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 00:00:00 | ||
图片预览




文档简介
六年级下册数学—圆柱表面积培优训练
姓名:________班级:________学校:_________成绩:___________
一、选择题
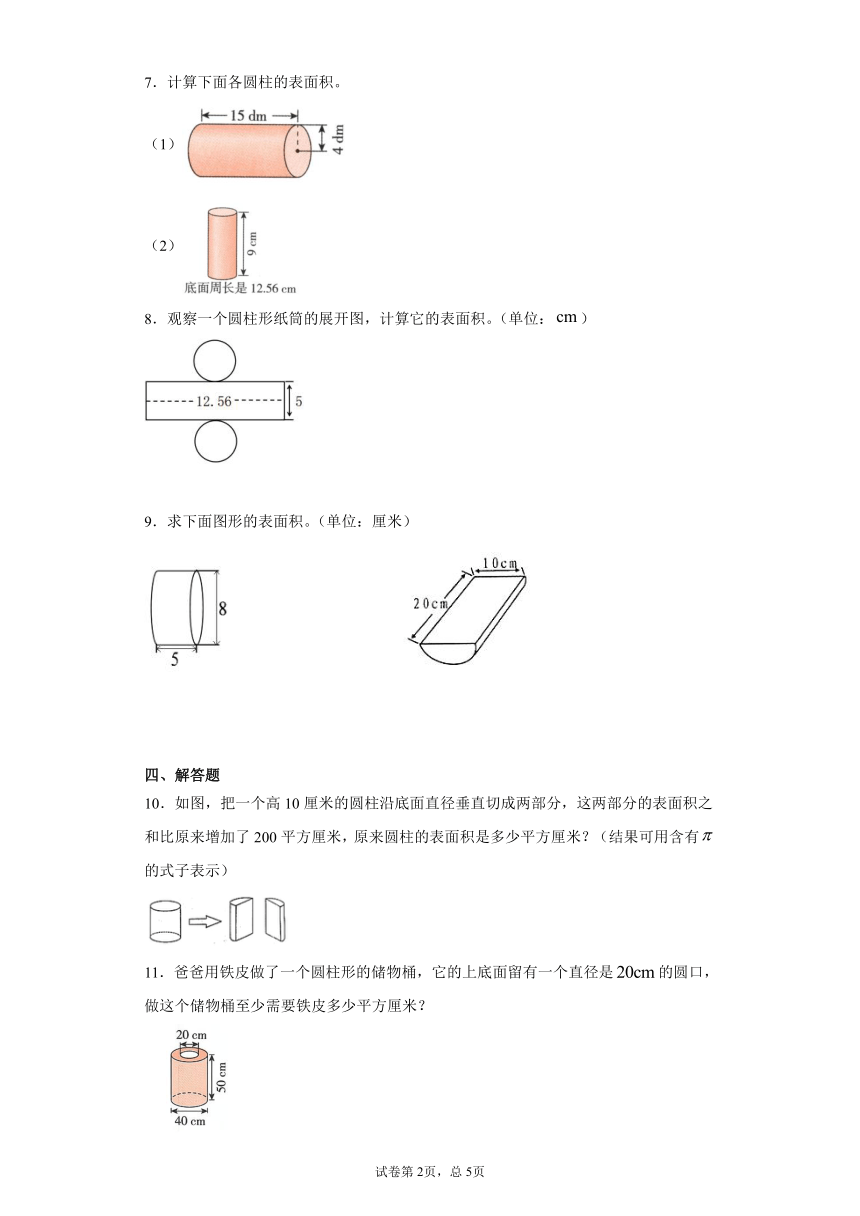
1.一个圆柱的侧面展开后是一个正方形,这个圆柱的底面直径与高的比是(
)。
A.
B.
C.
D.
2.把一个底面半径是4cm,高是6cm的圆柱切拼成一个近似的长方体,表面积增加了(
)cm。
A.50.24
B.24
C.48
二、填空题
3.下面是对同一个圆柱(底面半径为,高为)的两种不同切法(都是平均切成相同的两块)。甲种切法,表面积的和比原来增加(________);乙种切法,表面积的和比原来增加(________)。
4.如图,把一个圆柱切成若干等份,拼成一个近似的长方体,圆柱的侧面积是(________)。
5.圆柱的侧面积=(______)×(______),圆柱的表面积=(______)+(______)。
三、图形计算
6.求下面立体图形的表面积。
7.计算下面各圆柱的表面积。
(1)
(2)
8.观察一个圆柱形纸筒的展开图,计算它的表面积。(单位:)
9.求下面图形的表面积。(单位:厘米)
四、解答题
10.如图,把一个高10厘米的圆柱沿底面直径垂直切成两部分,这两部分的表面积之和比原来增加了200平方厘米,原来圆柱的表面积是多少平方厘米?(结果可用含有的式子表示)
11.爸爸用铁皮做了一个圆柱形的储物桶,它的上底面留有一个直径是的圆口,做这个储物桶至少需要铁皮多少平方厘米?
12.一个圆柱被截去后,圆柱的表面积减少了(如下图),原来圆柱的表面积是多少平方厘米?
13.如图,在一张长方形纸上,剪下阴影部分可围成一个圆柱,求这个圆柱的表面积。
14.下图是一张长方形纸,长,宽。如果以长边所在的直线为轴旋转一周得到一个圆柱,那么圆柱的表面积是多少平方厘米?
15.把一张长方形纸片按如图所示方法剪开后,正好可以做成一个圆柱,做成的圆柱的底面直径和底面周长分别是多少分米?
16.把一个高为5厘米的圆柱从直径处沿高剖成两上半圆柱,这两个半圆柱的表面积比原来增加80平方厘米,求原来圆柱的表面积。
17.一个圆柱形的罐头盒,高12.56厘米,它的侧面展开图是一个正方形,做5个这样的罐头盒,至少需要多少平方厘米的铁皮?
18.一个圆柱体的侧面积是62.8平方米,高和底面半径相等,求表面积.
19.把一个底面半径6分米,高1米的圆柱切成3个小圆柱,表面积增加了多少?
20.下图是一个圆柱形蛋糕盒,底面半径是15厘米,高20厘米.
(1)做这个蛋糕盒大约需要多少平方厘米的纸板?
(2)像上图那样用彩带包扎这个蛋糕盒,至少需要彩带多少厘米?(打结处大约用
15厘米彩带)
21.一根圆柱形木材长20分米,分成4个相等的圆柱体,表面积增加了18.84平方分米.原来圆柱形木材的表面积是多少?
22.一个圆柱体形的蓄水池,从里面量底面周长31.4米,深2.4米,在它的内壁与底面抹上水泥。抹水泥部分的面积是多少平方米?
23.要建造一个直径是8米,深1.5米的圆柱形鱼池,这个鱼池占地面积是多少平方米?
24.如图,一个圆柱体被截去5cm后,圆柱的表面积减少了31.4cm2,求原来圆柱体的表面积是多少平方厘米。
25.一台压路机的前轮是圆柱形,轮宽2米,直径1.2米。如果每分钟转动8周,那么每分钟能压路多少平方米?(最后结果保留整数)
26.加工一个无盖的圆柱形容器,底面周长是,高是。做一个这样的容器,准备的材料够不够?
27.有一个圆柱形水池,水池内壁和底面都要镶上瓷砖,水池的底面直径是6m,池深1.2m。镶瓷砖的面积是多少平方米?
28.学校为实验教室配备了一只无盖的圆柱形铁皮消防桶。做这只消防桶至少需要铁皮多少平方分米?
29.一根长1米,横截面直径是20厘米的木头浮在水面上,小明发现它正好是一半露出水面,请你求出这根木头与水接触的面的面积是多少?
30.将高都是1米,底面半径分别是1.5米、1米和0.5米的三个圆柱体组成一个物体,求它的表面积。
试卷第1页,总3页
试卷第1页,总3页
参考答案
1.A【分析】
由圆柱体的侧面展开图是一个正方形可知,圆柱体的高和底面周长相等,由此写出圆柱底面直径与高的比并化简即可。
【详解】底面周长即圆柱的高等于πd;
圆柱底面直径与高的比是:d∶πd=1∶π。
故答案为:A
【点睛】此题主要考查圆柱体的侧面展开图的形状,以及展开图的长和宽与圆柱体的底面周长和高的关系。
2.C【分析】把圆柱切拼成近似长方体,表面积增加了两个长方形,长方形的长是圆柱的高,长方形的宽是底面半径,据此求出一个长方形面积,乘2即可。
【详解】6×4×2=48(平方厘米)故答案为:C
【点睛】本题考查了圆柱表面积,圆柱表面积=底面积×2+侧面积。
3.2πr2
4rh
【分析】如果把圆柱平行于底面进行切分,切面是两个完全相同的圆,它与圆柱的底面完全相同;如果将圆柱沿底面直径垂直于底面进行切分,切面是两个完全相同的长方形(或正方形)。长方形的长和宽(或正方形的边长)分别是圆柱的底面直径和高。
【详解】由分析得:甲种切法:2×π×r2=2πr2
乙种切法:2r×h×2=4rh
【点睛】结合图示可以清楚地观察到两种不同的切法所形成的不同图形,图形的各要素与圆柱的半径、高相关,故可利用其来计算增加的表面积。
4.50.24【分析】
将圆柱切拼成一个近似的长方体后,可以看出圆柱的侧面积就是近似长方体的前后两个面的面积和。根据题图中的数据可以求出近似长方体的前后两个面的面积和即可。
【详解】
6.28×4×2
=6.28×8
=50.24(平方厘米)
【点睛】解答本题的关键是理解“圆柱的侧面积就是近似长方体的前后两个面的面积和”。
5.底面周长
高
2底面面积
侧面积
【分析】圆柱的侧面积是指围成圆柱的曲面的面积,而圆柱的表面积是指围成圆柱的所有面的面积,由此即可知道答案
【详解】①沿着圆柱形的高剪开,得到一个长方形,根据圆柱的侧面积定义,知道长方形的面积就是圆柱的侧面积,长方形的长是圆柱的底面周长,长方形的宽就是圆柱的高,所以,圆柱的侧面积=底面周长×高;②圆柱是由两个平面(两个圆面)和一个曲面组成的,2个圆的面积就是两个底面积,1个曲面就是圆柱的侧面积,所以,圆柱的表面积=2底面积+侧面积,
故答案为:底面周长,高,2底面面积,侧面积.
【点睛】牢记公式即可,基础题。
6.483.56cm2
【分析】通过观察可知,该图形的表面积等于外侧面积加上内侧面积再加上两个圆环的面积,由此解答即可。
【详解】
=251.2+188.4
=439.6(平方厘米);
=3.14×7
=21.98(平方厘米);
=439.6+43.96
=483.56(平方厘米)
7.(1)477.28dm2;(2)138.16
cm2
【分析】
根据“圆柱表面积=侧面积+底面积”可求得圆柱的表面积。
【详解】
(1)3.14×2×4×15+3.14×42×2
=3.14×120+3.14×32
=3.14×152
=477.28(dm2)
(2)12.56÷3.14÷2
=4÷2
=2(cm)
12.56×9+3.14×22×2
=113.04+25.12
=138.16(cm2)
8.87.92cm2
【分析】
圆柱的表面积=侧面积+底面积×2,侧面积=长×宽,圆的周长=长方形的长,圆柱的底面半径:圆的周长÷π÷2,底面积S=πr2,把数据分别代入公式解答即可。
【详解】
圆柱的底面半径:
12.56÷3.14÷2=2(厘米)
圆柱的表面积:
12.56×5+3.14×22×2
=62.8+3.14×4×2
=62.8+25.12
=87.92(cm2)
答:表面积是87.92cm2。
【点睛】
此题主要考查圆柱的表面积公式的灵活运用。
9.226.08cm2;592.5cm2
【分析】
(1)圆柱的表面积=圆柱的底面积×2+圆柱的侧面积,即字母公式:S柱=2πr2+πdh;代入数据计算即可。
(2)半个圆柱的表面积=圆柱的底面积+圆柱的侧面积的一半+长方形的面积;代入数据计算即可。
【详解】
(1)2×3.14×2+3.14×8×5
=2×3.14×16+3.14×8×5
=3.14×(2×16+8×5)
=3.14×72
=226.08(cm2)
(2)圆柱的底面积:3.14×2
=3.14×25
=78.5(cm2)
圆柱的侧面积的一半:3.14×10×20÷2=314(cm2)
长方形的面积:10×20=200(cm2)
半个圆柱的表面积:78.5+314+200=592.5(cm2)
【点睛】
根据图形特点灵活运用圆柱的表面积公式。
10.150π平方厘米
【分析】
“将一个圆柱体沿着底面直径切成两部分,表面积增加了200平方厘米”,就是增加了两个长是圆柱的高,宽是圆柱的底面直径的长方形;据此可求出圆柱的底面直径,然后再根据圆柱的表面积公式进行计算。
【详解】
200÷2=100(平方厘米)
100÷10=10(厘米)
π×10×10+π×(10÷2)2×2
=100π+50π
=150π(平方厘米)
答:原来圆柱的表面积是150π平方厘米。
【点睛】
本题的关键是理解:“将一个圆柱体沿着底面直径切成两个半圆柱,表面积增加了200平方厘米”,就是增加了两个长是圆柱的高,宽是圆柱的底面直径的长方形的面积。
11.
【分析】
求做这个储物桶至少需要铁皮多少平方厘米,就是求圆柱的表面积减去上底面的圆口的面积,先根据“圆柱表面积=侧面积+底面积”求出圆柱的表面积,再减去上底面的圆口的面积。
【详解】
答:做这个储物桶至少需要铁皮。
【点睛】
结合图示能够明确,储物桶的表面积由哪几部分组成,然后代入相关数据计算即可。
12.163.28cm2
【分析】
由题意可知,表面积减少的是高的圆柱的侧面积,用减少的面积除以10求出底面周长,再根据圆的周长公式求出底面半径,然后根据“圆柱表面积=侧面积十底面积×2”可求出圆柱的表面积。
【详解】
底面周长:62.8÷10=6.28(cm)
底面半径:6.28÷3.14÷2
=2÷2
=1(cm)
原来的表面积:3.14×12×2+6.28×(10+15)
=6.28+6.28×25
=6.28+157
=163.28(cm2)
答:原来圆柱的表面积是163.28平方厘米。
【点睛】
本题主要考查圆柱的表面积公式,解题的关键是求出圆柱的底面半径。
13.276.32cm2,
【分析】
求圆柱的表面积需要分别求出侧面积和底面积,圆柱的侧面展开图是长方形,长方形的长是25.12cm,但宽未知,需用长方形纸的宽减去圆柱底面的直径,如题图所示,长方形纸的长即为圆柱的底面周长,可以据此求出圆柱底面的直径,即25.12÷3.14=8(厘米),再利用此条件分别求出侧面积和底面积,再把它们相加即可。
【详解】
25.12÷3.14=8(cm)
15-8=7(cm)
25.12×7=175.84(cm2)
8÷2=4(cm)
3.14×4×4×2
=50.24×2
=100.48(cm2)
175.84+100.48=276.32(cm2)
答:这个圆柱的表面积是276.32cm2。
【分析】
本题是考查图形的切拼问题,圆柱表面积还有侧面积的计算,关键是求出圆柱的底面直径,同时要注意,圆柱的表面积是两个底面的面积加上一个侧面的面积。
14.1381.6平方厘米
【分析】
以长边所在的直线为轴旋转一周可得到一个底面半径为、高为的圆柱,其表面积为上、下两个底面的面积与侧面积之和。
【详解】
3.14×102×2+3.14×10×2×12
=3.14×200+3.14×240
=3.14×440
=1381.6(平方厘米)
答:圆柱的表面积是1381.6平方厘米。
【点睛】
本题主要考查圆柱的表面积公式,解题的关键是明确圆柱的底面半径与高的值。
15.底面直径;底面周长
【分析】
本题通过设未知数可以让等量关系更清晰。由题图可知长方形的宽等于圆柱的底面直径的2倍,而圆柱的底面周长是底面直径的3.14倍,因此长方形的宽不可能是圆柱的底面周长,圆柱的底面周长只能是长方形的长。因为长方形的长等于圆柱的底面周长,所以长方形的长就是圆柱底面直径的3.14倍。由题图可知长方形的长加上圆柱的底面直径等于,设做成的圆柱的底面直径是d分米,则长方形的长就是3.14d分米。可列方程d+3.14d=8.28,由此求出底面直径,进而求出周长即可。
【详解】
解:设做成的圆柱的底面直径是d分米;
d+3.14d=8.28
4.14d=8.28
d=2
;
答:做成的圆柱的底面直径是,底面周长是。
【点睛】
解答本题的关键是通过圆柱的底面周长是底面直径的3.14倍,排除宽的长度不可能是底面周长,明确圆柱的底面周长只能是长方形的长,进而根据公式求出底面直径和周长。
16.226.08平方厘米
【分析】
这两个半圆柱的表面积比原来增加80平方厘米,用80除以2再除以5可求出这个圆柱的直径,然后再根据圆柱表面积的计算方法进行计算。
【详解】
圆柱的直径是:80÷2÷5=8(厘米)
圆柱的表面积是:3.14×(8÷2)2×2+3.14×8×5
=3.14×16×2+3.14×8×5
=100.48+125.6
=226.08(平方厘米)
答:原来圆柱的表面是226.08平方厘米。
【点睛】
本题的关键是根据两个半圆柱的表面积比原来增加80平方厘米,求出圆柱的底面直径,再根据圆柱表面积的计算方法进行计算。
17.914.368平方厘米
【分析】
要求需要的铁皮面积,就是求这个圆柱体的表面积,因为侧面展开图是正方形,可得底面周长与高相等都是12.56厘米,据此可以求出圆柱的底面半径,再根据圆柱的表面积=2πr2+2πrh求出一个罐头盒的表面积,再乘5即可。
【详解】
12.56÷3.14÷2=2(厘米),
3.14×22×2+12.56×12.56,
=25.12+157.7536,
=182.8736(平方厘米),
182.8736×5=914.368(平方厘米),
答:至少需要914.368平方厘米的铁皮。
【点睛】
解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决。
18.125.6m2
【解析】
试题分析:因为圆柱的侧面积S=ch=2πrh,又因为r=h,所以S=2πr2,即πr2=S,而πr2就是圆柱的底面积,即圆柱的底面积等S=×62.8,再根据圆柱的表面积的计算方法:表面积=侧面积+2个底面积,即可求出圆柱的表面积.
解:设高为h米,底面半径为r米,则
62.8=2πr?h,
因为h=r,
所以62.8=2πr?r
r2=10
S表面积=S侧+2S底=62.8+2×3.14×10=125.6(m2).
答:表面积为125.6m2.
点评:灵活利用圆柱的侧面积公式S=ch=2πrh与底面积公式S=πr2,结合题意,求出底面积,即可求出表面积.
19.452.16平方分米
【分析】
根据圆柱的切割特点可得,每切割一次,就增加2个圆柱的底面积,切成3段,需要切两次,所以表面积是增加了4个圆柱的底面积,据此即可解答.
【详解】
3.14×6×6×4,
=113.04×4,
=452.16(平方分米),
答:表面积增加了452.16平方分米.
20.(1)3297平方厘米
(2)215厘米
【详解】
(1)先求出圆柱体的侧面积,再求出底面的面积,然后相加就是圆柱的表面积.
解题过程如下,
3.14×15×2×20+3.14××2
=1884+1413
=3297(平方厘米)
答:做这个蛋糕盒大约需要3297平方厘米的纸板.
(2)
如图所示,彩带的长度是4条直径的长度,4条高的长度,再加上打结处大约用
15厘米的长度.
15×2×4+20×4+15
=120+80+15
=215(厘米)
答:至少需要彩带215厘米.
21.131.88平方分米
【解析】
试题分析:观察图形可知,把一根圆柱平均分成4个相等的圆柱体,表面积是增加了6个圆柱的底面的面积,据此可以求出一个底面的面积是:18.84÷6=3.14(平方分米),3.14÷3.14=1,又因为12=1,所以可得出这个圆柱的底面半径是1分米,据此根据圆柱的侧面积=2πrh,求出侧面积,再加上2个圆柱的底面积,即可得出原圆柱的表面积.
解:18.84÷6=3.14(平方分米),
3.14÷3.14=1,又因为12=1,所以可得出这个圆柱的底面半径是1分米,
3.14×1×2×20+3.14×2,
=125.6+6.28,
=131.88(平方分米),
答:原圆柱的表面积是131.88平方分米.
点评:根据圆柱增加的表面积求出这个圆柱的底面积,从而求出圆柱的底面半径是解决本题的关键.
22.153.86平方米
【分析】
抹水泥部分的面积就是这个圆柱形水池的表面积,即一个底面积和侧面积的和,由此先利用底面周长公式求出这个水池的底面半径,再利用侧面积公式和圆的面积公式即可解答。
【详解】
底面半径是:31.4÷3.14÷2=5(米)
底面积是:3.14×52
=3.14×25
=78.5(平方米)
侧面积是:3.14×5×2×2.4=75.36(平方米)
所以抹水泥的面积是:78.5+75.36=153.86(平方米)
答:抹水泥的面积是153.86平方米。
【点睛】
解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决。
23.50.24平方米
【分析】
这个鱼池占地面积就是求圆柱的底面积,根据公式S=πr2代入数据计算即可。
【详解】
3.14×(8÷2)2
=3.14×16
=50.24(平方米)
答:这个鱼池占地面积是50.24平方米。
【点睛】
此题考查圆柱表面积的实际应用,根据实际情况灵活选择公式。
24.131.88平方厘米
【分析】
表面积减少的数除以高减少的数,得到圆柱的底面周长,由底面周长可求底面半径,进而可求底面积,底面周长乘以高可得侧面积,两个底面积加侧面积得表面积。
【详解】
底面周长:31.4÷5=6.28(厘米),
底面半径:6.28÷3.14÷2=1(厘米),
两个底面积:3.14×12×2=6.28(平方厘米),
侧面积:6.28×20=125.6(平方厘米),
表面积:125.6+6.28=131.88(平方厘米)。
答:原来圆柱的表面积是131.88平方厘米。
【点睛】
关键从高减少,表面积减少的是侧面的面积切入进行解答。
25.60平方米
【分析】
先求出压路机转动一周压路多少平方米,即用圆柱的底面周长乘高,再乘8周的压路面积即可。
【详解】
3.14×1.2×2×8
=3.768×2×8
=7.536×8
≈60(平方米)
答:每分钟能压路60平方米。
【点睛】
求出压路机转动一周的压路面积是解答本题的关键。
26.不够
【分析】
问准备的材料够不够,可以先求圆柱侧面积加上圆柱一个底面的面积的和,再与准备的材料比较。根据圆柱的侧面积=底面周长×高,圆柱的底面积=πr2,圆柱的底面半径可由圆的周长公式:r=C÷π÷2求解。通过比较,即可得出结果。
【详解】
18.84×7=131.88(dm2)
18.84÷3.14÷2
=6÷2
=3(dm)
3.14×3×3
=9.42×3
=28.26(dm2)
131.88+28.26=160.14(dm2)
160.14
dm2=1.6014m2
1.6014m2>1.6m2
答:准备的材料不够。
【点睛】
解答此题的关键是明白:求需要的材料面积,实际上是求容器的侧面积加上底面积,熟练掌握圆柱的侧面积还有底面积的公式,并灵活运用。
27.50.868平方米
【分析】
水池没有上边的面,用一个底面积+侧面积即可。
【详解】
6÷2=3(米)
3.14×3+3.14×6×1.2
=28.26+22.608
=50.868(平方米)
答:镶瓷砖的面积是50.868平方米。
【点睛】
本题考查了圆柱表面积,圆柱侧面积=底面周长×高。
28.75.36平方分米
【分析】
要求做这只消防桶需要多少铁皮,就是要求这个圆柱形桶的表面积,无盖圆柱的表面积=侧面积+底面积。
【详解】
3.14×4×5+3.14×(4÷2)2
=3.14×20+3.14×4
=3.14×24
=75.36(平方分米)
答:做这只消防桶至少需要铁皮75.36平方分米。
【点睛】
本题考查圆柱的表面积的应用,计算时注意,无盖要少算一个底面。
29.3454平方厘米
【分析】
根据题意,这根木头与水接触的面的面积就是这根圆柱体木头表面积的一半,可根据圆柱的表面积公式进行计算即可得到答案。
【详解】
木头横截面的半径为:20÷2=10(厘米),
两个底面积:3.14×102×2=628(平方厘米),
侧面积:3.14×20×100
=62.8×100,
=6280(平方厘米),
表面积:628+6280=6908(平方厘米),
与水接触的面积:6908÷2=3454(平方厘米)
答:这根木头与水接触的面的面积是3454平方厘米。
【点睛】
本题主要考查圆柱的表面积,明确所求的内容为圆柱表面积的一半是解题的关键。
30.32.97平方米
【分析】
这个物体的表面积是大圆柱的表面积加上中、小圆柱的侧面积,根据公式计算即可。
【详解】
大圆柱的表面积:
3.14×1.52×2+2×3.14×1.5×1
=14.13+9.42
=23.55(平方米),
中圆柱侧面积:2×3.14×1×1=6.28(平方米),
小圆柱侧面积:2×3.14×0.5×1=3.14(平方米),
这个物体的表面积:23.55+6.28+3.14=32.97(平方米);
答:这个物体的表面积是32.97平方米。
【点睛】
此题主要考查圆柱的侧面积、表面积公式及其计算。
答案第1页,总2页
答案第1页,总2页
姓名:________班级:________学校:_________成绩:___________
一、选择题
1.一个圆柱的侧面展开后是一个正方形,这个圆柱的底面直径与高的比是(
)。
A.
B.
C.
D.
2.把一个底面半径是4cm,高是6cm的圆柱切拼成一个近似的长方体,表面积增加了(
)cm。
A.50.24
B.24
C.48
二、填空题
3.下面是对同一个圆柱(底面半径为,高为)的两种不同切法(都是平均切成相同的两块)。甲种切法,表面积的和比原来增加(________);乙种切法,表面积的和比原来增加(________)。
4.如图,把一个圆柱切成若干等份,拼成一个近似的长方体,圆柱的侧面积是(________)。
5.圆柱的侧面积=(______)×(______),圆柱的表面积=(______)+(______)。
三、图形计算
6.求下面立体图形的表面积。
7.计算下面各圆柱的表面积。
(1)
(2)
8.观察一个圆柱形纸筒的展开图,计算它的表面积。(单位:)
9.求下面图形的表面积。(单位:厘米)
四、解答题
10.如图,把一个高10厘米的圆柱沿底面直径垂直切成两部分,这两部分的表面积之和比原来增加了200平方厘米,原来圆柱的表面积是多少平方厘米?(结果可用含有的式子表示)
11.爸爸用铁皮做了一个圆柱形的储物桶,它的上底面留有一个直径是的圆口,做这个储物桶至少需要铁皮多少平方厘米?
12.一个圆柱被截去后,圆柱的表面积减少了(如下图),原来圆柱的表面积是多少平方厘米?
13.如图,在一张长方形纸上,剪下阴影部分可围成一个圆柱,求这个圆柱的表面积。
14.下图是一张长方形纸,长,宽。如果以长边所在的直线为轴旋转一周得到一个圆柱,那么圆柱的表面积是多少平方厘米?
15.把一张长方形纸片按如图所示方法剪开后,正好可以做成一个圆柱,做成的圆柱的底面直径和底面周长分别是多少分米?
16.把一个高为5厘米的圆柱从直径处沿高剖成两上半圆柱,这两个半圆柱的表面积比原来增加80平方厘米,求原来圆柱的表面积。
17.一个圆柱形的罐头盒,高12.56厘米,它的侧面展开图是一个正方形,做5个这样的罐头盒,至少需要多少平方厘米的铁皮?
18.一个圆柱体的侧面积是62.8平方米,高和底面半径相等,求表面积.
19.把一个底面半径6分米,高1米的圆柱切成3个小圆柱,表面积增加了多少?
20.下图是一个圆柱形蛋糕盒,底面半径是15厘米,高20厘米.
(1)做这个蛋糕盒大约需要多少平方厘米的纸板?
(2)像上图那样用彩带包扎这个蛋糕盒,至少需要彩带多少厘米?(打结处大约用
15厘米彩带)
21.一根圆柱形木材长20分米,分成4个相等的圆柱体,表面积增加了18.84平方分米.原来圆柱形木材的表面积是多少?
22.一个圆柱体形的蓄水池,从里面量底面周长31.4米,深2.4米,在它的内壁与底面抹上水泥。抹水泥部分的面积是多少平方米?
23.要建造一个直径是8米,深1.5米的圆柱形鱼池,这个鱼池占地面积是多少平方米?
24.如图,一个圆柱体被截去5cm后,圆柱的表面积减少了31.4cm2,求原来圆柱体的表面积是多少平方厘米。
25.一台压路机的前轮是圆柱形,轮宽2米,直径1.2米。如果每分钟转动8周,那么每分钟能压路多少平方米?(最后结果保留整数)
26.加工一个无盖的圆柱形容器,底面周长是,高是。做一个这样的容器,准备的材料够不够?
27.有一个圆柱形水池,水池内壁和底面都要镶上瓷砖,水池的底面直径是6m,池深1.2m。镶瓷砖的面积是多少平方米?
28.学校为实验教室配备了一只无盖的圆柱形铁皮消防桶。做这只消防桶至少需要铁皮多少平方分米?
29.一根长1米,横截面直径是20厘米的木头浮在水面上,小明发现它正好是一半露出水面,请你求出这根木头与水接触的面的面积是多少?
30.将高都是1米,底面半径分别是1.5米、1米和0.5米的三个圆柱体组成一个物体,求它的表面积。
试卷第1页,总3页
试卷第1页,总3页
参考答案
1.A【分析】
由圆柱体的侧面展开图是一个正方形可知,圆柱体的高和底面周长相等,由此写出圆柱底面直径与高的比并化简即可。
【详解】底面周长即圆柱的高等于πd;
圆柱底面直径与高的比是:d∶πd=1∶π。
故答案为:A
【点睛】此题主要考查圆柱体的侧面展开图的形状,以及展开图的长和宽与圆柱体的底面周长和高的关系。
2.C【分析】把圆柱切拼成近似长方体,表面积增加了两个长方形,长方形的长是圆柱的高,长方形的宽是底面半径,据此求出一个长方形面积,乘2即可。
【详解】6×4×2=48(平方厘米)故答案为:C
【点睛】本题考查了圆柱表面积,圆柱表面积=底面积×2+侧面积。
3.2πr2
4rh
【分析】如果把圆柱平行于底面进行切分,切面是两个完全相同的圆,它与圆柱的底面完全相同;如果将圆柱沿底面直径垂直于底面进行切分,切面是两个完全相同的长方形(或正方形)。长方形的长和宽(或正方形的边长)分别是圆柱的底面直径和高。
【详解】由分析得:甲种切法:2×π×r2=2πr2
乙种切法:2r×h×2=4rh
【点睛】结合图示可以清楚地观察到两种不同的切法所形成的不同图形,图形的各要素与圆柱的半径、高相关,故可利用其来计算增加的表面积。
4.50.24【分析】
将圆柱切拼成一个近似的长方体后,可以看出圆柱的侧面积就是近似长方体的前后两个面的面积和。根据题图中的数据可以求出近似长方体的前后两个面的面积和即可。
【详解】
6.28×4×2
=6.28×8
=50.24(平方厘米)
【点睛】解答本题的关键是理解“圆柱的侧面积就是近似长方体的前后两个面的面积和”。
5.底面周长
高
2底面面积
侧面积
【分析】圆柱的侧面积是指围成圆柱的曲面的面积,而圆柱的表面积是指围成圆柱的所有面的面积,由此即可知道答案
【详解】①沿着圆柱形的高剪开,得到一个长方形,根据圆柱的侧面积定义,知道长方形的面积就是圆柱的侧面积,长方形的长是圆柱的底面周长,长方形的宽就是圆柱的高,所以,圆柱的侧面积=底面周长×高;②圆柱是由两个平面(两个圆面)和一个曲面组成的,2个圆的面积就是两个底面积,1个曲面就是圆柱的侧面积,所以,圆柱的表面积=2底面积+侧面积,
故答案为:底面周长,高,2底面面积,侧面积.
【点睛】牢记公式即可,基础题。
6.483.56cm2
【分析】通过观察可知,该图形的表面积等于外侧面积加上内侧面积再加上两个圆环的面积,由此解答即可。
【详解】
=251.2+188.4
=439.6(平方厘米);
=3.14×7
=21.98(平方厘米);
=439.6+43.96
=483.56(平方厘米)
7.(1)477.28dm2;(2)138.16
cm2
【分析】
根据“圆柱表面积=侧面积+底面积”可求得圆柱的表面积。
【详解】
(1)3.14×2×4×15+3.14×42×2
=3.14×120+3.14×32
=3.14×152
=477.28(dm2)
(2)12.56÷3.14÷2
=4÷2
=2(cm)
12.56×9+3.14×22×2
=113.04+25.12
=138.16(cm2)
8.87.92cm2
【分析】
圆柱的表面积=侧面积+底面积×2,侧面积=长×宽,圆的周长=长方形的长,圆柱的底面半径:圆的周长÷π÷2,底面积S=πr2,把数据分别代入公式解答即可。
【详解】
圆柱的底面半径:
12.56÷3.14÷2=2(厘米)
圆柱的表面积:
12.56×5+3.14×22×2
=62.8+3.14×4×2
=62.8+25.12
=87.92(cm2)
答:表面积是87.92cm2。
【点睛】
此题主要考查圆柱的表面积公式的灵活运用。
9.226.08cm2;592.5cm2
【分析】
(1)圆柱的表面积=圆柱的底面积×2+圆柱的侧面积,即字母公式:S柱=2πr2+πdh;代入数据计算即可。
(2)半个圆柱的表面积=圆柱的底面积+圆柱的侧面积的一半+长方形的面积;代入数据计算即可。
【详解】
(1)2×3.14×2+3.14×8×5
=2×3.14×16+3.14×8×5
=3.14×(2×16+8×5)
=3.14×72
=226.08(cm2)
(2)圆柱的底面积:3.14×2
=3.14×25
=78.5(cm2)
圆柱的侧面积的一半:3.14×10×20÷2=314(cm2)
长方形的面积:10×20=200(cm2)
半个圆柱的表面积:78.5+314+200=592.5(cm2)
【点睛】
根据图形特点灵活运用圆柱的表面积公式。
10.150π平方厘米
【分析】
“将一个圆柱体沿着底面直径切成两部分,表面积增加了200平方厘米”,就是增加了两个长是圆柱的高,宽是圆柱的底面直径的长方形;据此可求出圆柱的底面直径,然后再根据圆柱的表面积公式进行计算。
【详解】
200÷2=100(平方厘米)
100÷10=10(厘米)
π×10×10+π×(10÷2)2×2
=100π+50π
=150π(平方厘米)
答:原来圆柱的表面积是150π平方厘米。
【点睛】
本题的关键是理解:“将一个圆柱体沿着底面直径切成两个半圆柱,表面积增加了200平方厘米”,就是增加了两个长是圆柱的高,宽是圆柱的底面直径的长方形的面积。
11.
【分析】
求做这个储物桶至少需要铁皮多少平方厘米,就是求圆柱的表面积减去上底面的圆口的面积,先根据“圆柱表面积=侧面积+底面积”求出圆柱的表面积,再减去上底面的圆口的面积。
【详解】
答:做这个储物桶至少需要铁皮。
【点睛】
结合图示能够明确,储物桶的表面积由哪几部分组成,然后代入相关数据计算即可。
12.163.28cm2
【分析】
由题意可知,表面积减少的是高的圆柱的侧面积,用减少的面积除以10求出底面周长,再根据圆的周长公式求出底面半径,然后根据“圆柱表面积=侧面积十底面积×2”可求出圆柱的表面积。
【详解】
底面周长:62.8÷10=6.28(cm)
底面半径:6.28÷3.14÷2
=2÷2
=1(cm)
原来的表面积:3.14×12×2+6.28×(10+15)
=6.28+6.28×25
=6.28+157
=163.28(cm2)
答:原来圆柱的表面积是163.28平方厘米。
【点睛】
本题主要考查圆柱的表面积公式,解题的关键是求出圆柱的底面半径。
13.276.32cm2,
【分析】
求圆柱的表面积需要分别求出侧面积和底面积,圆柱的侧面展开图是长方形,长方形的长是25.12cm,但宽未知,需用长方形纸的宽减去圆柱底面的直径,如题图所示,长方形纸的长即为圆柱的底面周长,可以据此求出圆柱底面的直径,即25.12÷3.14=8(厘米),再利用此条件分别求出侧面积和底面积,再把它们相加即可。
【详解】
25.12÷3.14=8(cm)
15-8=7(cm)
25.12×7=175.84(cm2)
8÷2=4(cm)
3.14×4×4×2
=50.24×2
=100.48(cm2)
175.84+100.48=276.32(cm2)
答:这个圆柱的表面积是276.32cm2。
【分析】
本题是考查图形的切拼问题,圆柱表面积还有侧面积的计算,关键是求出圆柱的底面直径,同时要注意,圆柱的表面积是两个底面的面积加上一个侧面的面积。
14.1381.6平方厘米
【分析】
以长边所在的直线为轴旋转一周可得到一个底面半径为、高为的圆柱,其表面积为上、下两个底面的面积与侧面积之和。
【详解】
3.14×102×2+3.14×10×2×12
=3.14×200+3.14×240
=3.14×440
=1381.6(平方厘米)
答:圆柱的表面积是1381.6平方厘米。
【点睛】
本题主要考查圆柱的表面积公式,解题的关键是明确圆柱的底面半径与高的值。
15.底面直径;底面周长
【分析】
本题通过设未知数可以让等量关系更清晰。由题图可知长方形的宽等于圆柱的底面直径的2倍,而圆柱的底面周长是底面直径的3.14倍,因此长方形的宽不可能是圆柱的底面周长,圆柱的底面周长只能是长方形的长。因为长方形的长等于圆柱的底面周长,所以长方形的长就是圆柱底面直径的3.14倍。由题图可知长方形的长加上圆柱的底面直径等于,设做成的圆柱的底面直径是d分米,则长方形的长就是3.14d分米。可列方程d+3.14d=8.28,由此求出底面直径,进而求出周长即可。
【详解】
解:设做成的圆柱的底面直径是d分米;
d+3.14d=8.28
4.14d=8.28
d=2
;
答:做成的圆柱的底面直径是,底面周长是。
【点睛】
解答本题的关键是通过圆柱的底面周长是底面直径的3.14倍,排除宽的长度不可能是底面周长,明确圆柱的底面周长只能是长方形的长,进而根据公式求出底面直径和周长。
16.226.08平方厘米
【分析】
这两个半圆柱的表面积比原来增加80平方厘米,用80除以2再除以5可求出这个圆柱的直径,然后再根据圆柱表面积的计算方法进行计算。
【详解】
圆柱的直径是:80÷2÷5=8(厘米)
圆柱的表面积是:3.14×(8÷2)2×2+3.14×8×5
=3.14×16×2+3.14×8×5
=100.48+125.6
=226.08(平方厘米)
答:原来圆柱的表面是226.08平方厘米。
【点睛】
本题的关键是根据两个半圆柱的表面积比原来增加80平方厘米,求出圆柱的底面直径,再根据圆柱表面积的计算方法进行计算。
17.914.368平方厘米
【分析】
要求需要的铁皮面积,就是求这个圆柱体的表面积,因为侧面展开图是正方形,可得底面周长与高相等都是12.56厘米,据此可以求出圆柱的底面半径,再根据圆柱的表面积=2πr2+2πrh求出一个罐头盒的表面积,再乘5即可。
【详解】
12.56÷3.14÷2=2(厘米),
3.14×22×2+12.56×12.56,
=25.12+157.7536,
=182.8736(平方厘米),
182.8736×5=914.368(平方厘米),
答:至少需要914.368平方厘米的铁皮。
【点睛】
解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决。
18.125.6m2
【解析】
试题分析:因为圆柱的侧面积S=ch=2πrh,又因为r=h,所以S=2πr2,即πr2=S,而πr2就是圆柱的底面积,即圆柱的底面积等S=×62.8,再根据圆柱的表面积的计算方法:表面积=侧面积+2个底面积,即可求出圆柱的表面积.
解:设高为h米,底面半径为r米,则
62.8=2πr?h,
因为h=r,
所以62.8=2πr?r
r2=10
S表面积=S侧+2S底=62.8+2×3.14×10=125.6(m2).
答:表面积为125.6m2.
点评:灵活利用圆柱的侧面积公式S=ch=2πrh与底面积公式S=πr2,结合题意,求出底面积,即可求出表面积.
19.452.16平方分米
【分析】
根据圆柱的切割特点可得,每切割一次,就增加2个圆柱的底面积,切成3段,需要切两次,所以表面积是增加了4个圆柱的底面积,据此即可解答.
【详解】
3.14×6×6×4,
=113.04×4,
=452.16(平方分米),
答:表面积增加了452.16平方分米.
20.(1)3297平方厘米
(2)215厘米
【详解】
(1)先求出圆柱体的侧面积,再求出底面的面积,然后相加就是圆柱的表面积.
解题过程如下,
3.14×15×2×20+3.14××2
=1884+1413
=3297(平方厘米)
答:做这个蛋糕盒大约需要3297平方厘米的纸板.
(2)
如图所示,彩带的长度是4条直径的长度,4条高的长度,再加上打结处大约用
15厘米的长度.
15×2×4+20×4+15
=120+80+15
=215(厘米)
答:至少需要彩带215厘米.
21.131.88平方分米
【解析】
试题分析:观察图形可知,把一根圆柱平均分成4个相等的圆柱体,表面积是增加了6个圆柱的底面的面积,据此可以求出一个底面的面积是:18.84÷6=3.14(平方分米),3.14÷3.14=1,又因为12=1,所以可得出这个圆柱的底面半径是1分米,据此根据圆柱的侧面积=2πrh,求出侧面积,再加上2个圆柱的底面积,即可得出原圆柱的表面积.
解:18.84÷6=3.14(平方分米),
3.14÷3.14=1,又因为12=1,所以可得出这个圆柱的底面半径是1分米,
3.14×1×2×20+3.14×2,
=125.6+6.28,
=131.88(平方分米),
答:原圆柱的表面积是131.88平方分米.
点评:根据圆柱增加的表面积求出这个圆柱的底面积,从而求出圆柱的底面半径是解决本题的关键.
22.153.86平方米
【分析】
抹水泥部分的面积就是这个圆柱形水池的表面积,即一个底面积和侧面积的和,由此先利用底面周长公式求出这个水池的底面半径,再利用侧面积公式和圆的面积公式即可解答。
【详解】
底面半径是:31.4÷3.14÷2=5(米)
底面积是:3.14×52
=3.14×25
=78.5(平方米)
侧面积是:3.14×5×2×2.4=75.36(平方米)
所以抹水泥的面积是:78.5+75.36=153.86(平方米)
答:抹水泥的面积是153.86平方米。
【点睛】
解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决。
23.50.24平方米
【分析】
这个鱼池占地面积就是求圆柱的底面积,根据公式S=πr2代入数据计算即可。
【详解】
3.14×(8÷2)2
=3.14×16
=50.24(平方米)
答:这个鱼池占地面积是50.24平方米。
【点睛】
此题考查圆柱表面积的实际应用,根据实际情况灵活选择公式。
24.131.88平方厘米
【分析】
表面积减少的数除以高减少的数,得到圆柱的底面周长,由底面周长可求底面半径,进而可求底面积,底面周长乘以高可得侧面积,两个底面积加侧面积得表面积。
【详解】
底面周长:31.4÷5=6.28(厘米),
底面半径:6.28÷3.14÷2=1(厘米),
两个底面积:3.14×12×2=6.28(平方厘米),
侧面积:6.28×20=125.6(平方厘米),
表面积:125.6+6.28=131.88(平方厘米)。
答:原来圆柱的表面积是131.88平方厘米。
【点睛】
关键从高减少,表面积减少的是侧面的面积切入进行解答。
25.60平方米
【分析】
先求出压路机转动一周压路多少平方米,即用圆柱的底面周长乘高,再乘8周的压路面积即可。
【详解】
3.14×1.2×2×8
=3.768×2×8
=7.536×8
≈60(平方米)
答:每分钟能压路60平方米。
【点睛】
求出压路机转动一周的压路面积是解答本题的关键。
26.不够
【分析】
问准备的材料够不够,可以先求圆柱侧面积加上圆柱一个底面的面积的和,再与准备的材料比较。根据圆柱的侧面积=底面周长×高,圆柱的底面积=πr2,圆柱的底面半径可由圆的周长公式:r=C÷π÷2求解。通过比较,即可得出结果。
【详解】
18.84×7=131.88(dm2)
18.84÷3.14÷2
=6÷2
=3(dm)
3.14×3×3
=9.42×3
=28.26(dm2)
131.88+28.26=160.14(dm2)
160.14
dm2=1.6014m2
1.6014m2>1.6m2
答:准备的材料不够。
【点睛】
解答此题的关键是明白:求需要的材料面积,实际上是求容器的侧面积加上底面积,熟练掌握圆柱的侧面积还有底面积的公式,并灵活运用。
27.50.868平方米
【分析】
水池没有上边的面,用一个底面积+侧面积即可。
【详解】
6÷2=3(米)
3.14×3+3.14×6×1.2
=28.26+22.608
=50.868(平方米)
答:镶瓷砖的面积是50.868平方米。
【点睛】
本题考查了圆柱表面积,圆柱侧面积=底面周长×高。
28.75.36平方分米
【分析】
要求做这只消防桶需要多少铁皮,就是要求这个圆柱形桶的表面积,无盖圆柱的表面积=侧面积+底面积。
【详解】
3.14×4×5+3.14×(4÷2)2
=3.14×20+3.14×4
=3.14×24
=75.36(平方分米)
答:做这只消防桶至少需要铁皮75.36平方分米。
【点睛】
本题考查圆柱的表面积的应用,计算时注意,无盖要少算一个底面。
29.3454平方厘米
【分析】
根据题意,这根木头与水接触的面的面积就是这根圆柱体木头表面积的一半,可根据圆柱的表面积公式进行计算即可得到答案。
【详解】
木头横截面的半径为:20÷2=10(厘米),
两个底面积:3.14×102×2=628(平方厘米),
侧面积:3.14×20×100
=62.8×100,
=6280(平方厘米),
表面积:628+6280=6908(平方厘米),
与水接触的面积:6908÷2=3454(平方厘米)
答:这根木头与水接触的面的面积是3454平方厘米。
【点睛】
本题主要考查圆柱的表面积,明确所求的内容为圆柱表面积的一半是解题的关键。
30.32.97平方米
【分析】
这个物体的表面积是大圆柱的表面积加上中、小圆柱的侧面积,根据公式计算即可。
【详解】
大圆柱的表面积:
3.14×1.52×2+2×3.14×1.5×1
=14.13+9.42
=23.55(平方米),
中圆柱侧面积:2×3.14×1×1=6.28(平方米),
小圆柱侧面积:2×3.14×0.5×1=3.14(平方米),
这个物体的表面积:23.55+6.28+3.14=32.97(平方米);
答:这个物体的表面积是32.97平方米。
【点睛】
此题主要考查圆柱的侧面积、表面积公式及其计算。
答案第1页,总2页
答案第1页,总2页
