冀教版七年级数学下册6.4简单的三元一次方程组课时训练(Word版,含答案)
文档属性
| 名称 | 冀教版七年级数学下册6.4简单的三元一次方程组课时训练(Word版,含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 206.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 00:00:00 | ||
图片预览


文档简介
6.4简单的三元一次方程组课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.有三种文具,每种价格分别是3元、7元和4元,现在有27元钱,三种文具都要买,恰好使钱用完的买法数有( )种.
A.1 B.2 C.3 D.4
2.下列四组数值中,方程组的解是( )
A. B. C. D.
3.方程组的解是( )
A. B. C. D.
4.已知如果x与y互为相反数,那么(???? )
A. B. C. D.
5.一套数学题集共有100道题,甲、乙和丙三人分别作答,每道题至少有一人解对,且每人都解对了其中的60道.如果将其中只有1人解对的题称作难题,2人解对的题称作中档题,3人都解对的题称作容易题,那么下列判断一定正确的是( )
A.容易题和中档题共60道 B.难题比容易题多20道
C.难题比中档题多10道 D.中档题比容易题多15道
6.在“自主互助学习型课堂竞赛”中,为奖励表现突出的同学,初一(7)班利用班费元钱,购买钢笔、相册、笔记本三种奖品,其中钢笔至多买支,若钢笔每支元,相册每本元,笔记本每本元,在把钱都用尽的条件下,买法共有( )
A.种 B.种 C.种 D.种
7.下列方程组中,是三元一次方程组的是( )
A. B. C. D.
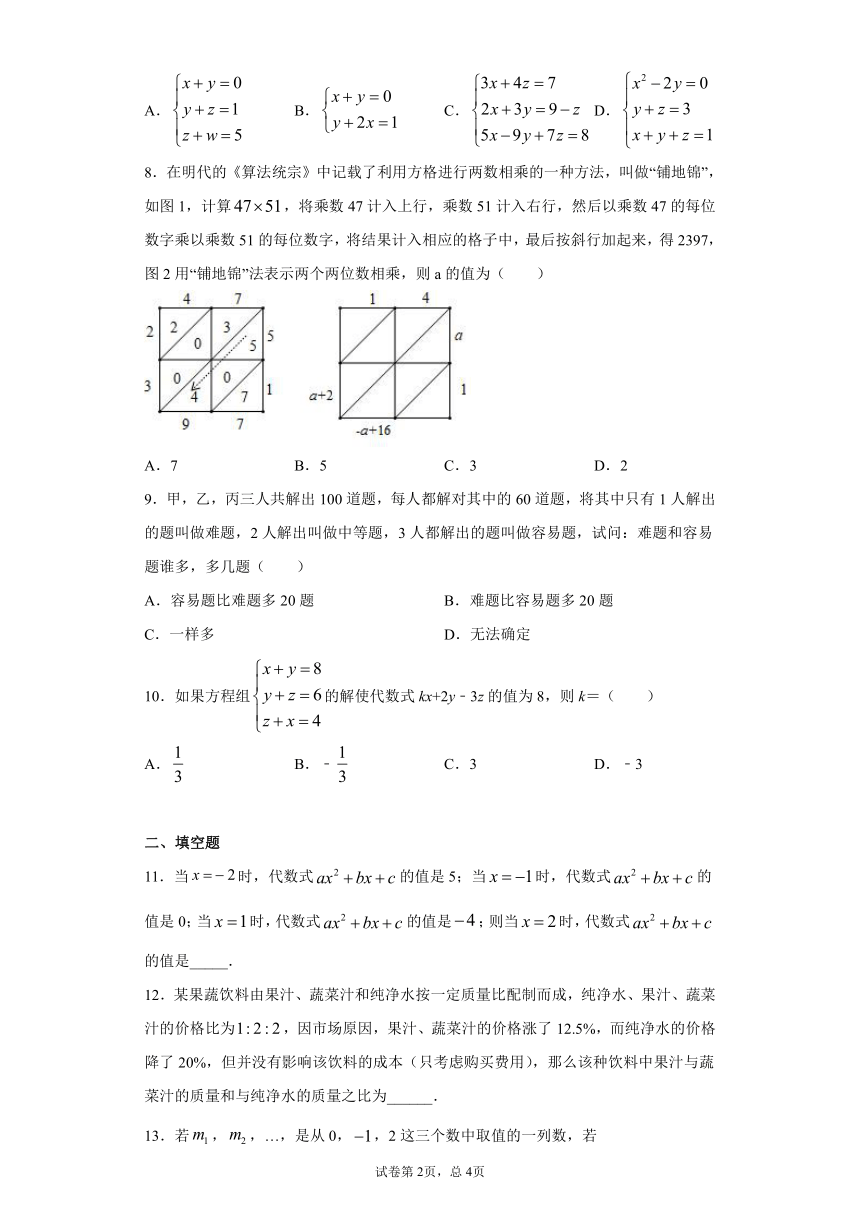
8.在明代的《算法统宗》中记载了利用方格进行两数相乘的一种方法,叫做“铺地锦”,如图1,计算,将乘数47计入上行,乘数51计入右行,然后以乘数47的每位数字乘以乘数51的每位数字,将结果计入相应的格子中,最后按斜行加起来,得2397,图2用“铺地锦”法表示两个两位数相乘,则a的值为( )
A.7 B.5 C.3 D.2
9.甲,乙,丙三人共解出100道题,每人都解对其中的60道题,将其中只有1人解出的题叫做难题,2人解出叫做中等题,3人都解出的题叫做容易题,试问:难题和容易题谁多,多几题( )
A.容易题比难题多20题 B.难题比容易题多20题
C.一样多 D.无法确定
10.如果方程组的解使代数式kx+2y﹣3z的值为8,则k=( )
A. B.﹣ C.3 D.﹣3
二、填空题
11.当时,代数式的值是5;当时,代数式的值是0;当时,代数式的值是;则当时,代数式的值是_____.
12.某果蔬饮料由果汁、蔬菜汁和纯净水按一定质量比配制而成,纯净水、果汁、蔬菜汁的价格比为,因市场原因,果汁、蔬菜汁的价格涨了12.5%,而纯净水的价格降了20%,但并没有影响该饮料的成本(只考虑购买费用),那么该种饮料中果汁与蔬菜汁的质量和与纯净水的质量之比为______.
13.若,,…,是从0,,2这三个数中取值的一列数,若,,则,,…,中为2的个数是______.
14.某水稻种植中心培育了甲、乙、丙三种水稻,将这三种水稻分别种植于三块大小各不相同的试验田里.去年,三种水稻的平均亩产量分别为300kg,500kg,400kg,总平均亩产量为450kg,且丙种水稻的的总产量是甲种水稻总产量的4倍,今年初,研究人员改良了水稻种子,仍按去年的方式种植,三种水稻的平均亩产量都增加了.总平均亩产量增长了40%,甲、丙两种水稻的总产量增长了30%,则乙种水稻平均亩产量的增长率为_______.
15.在刚刚结束的万州二中秋季运动会中,有一个趣味项目,分钟内运送三大筐数量相同的兵乓球,甲每 次从第一个大筐中取出个球;乙每次从第二个大筐中取出个球;丙则是每次从第三个大筐中取出个 球.比赛激烈最终三人都记不清各自取了多少次球了,最后裁判清点发现第一个筐中剩下个球,第二个筐剩下个球,第三个筐剩下个球,那么根据上述情况可以推知每个筐中至少有____________个兵乓球.
16.已知x,y,z都不为0,且,则式子的值为_____.
三、解答题
17.阅读理解:已知实数x,y满足3x﹣y=5…①,2x+3y=7…②,求x﹣4y和7x+5y的值.仔细观察两个方程未知数的系数之间的关系,本题可以通过适当变形整体求得代数式的值,如由①﹣②可得x﹣4y=﹣2,由①+②×2可得7x+5y=19.这样的解题思想就是通常所说的“整体思想”.利用“整体思想”,解决下列问题:
(1)已知二元一次方程组?,则x﹣y= ,x+y= ;
(2)买20支铅笔、3块橡皮、2本日记本共需32元,买39支铅笔、5块橡皮、3本日记本共需58元,求购买5支铅笔、5块橡皮5本日记本共需多少元?
(3)对于实数x,y,定义新运算:x*y=ax+by+c,其中a,b,c是常数,等式右边是实数运算.已知3*5=15,4*7=28,求1*1的值.
18.有一片牧场原有的草量为,草每天都匀速地生长,这片牧场每天牧草的生长量都为.若在其上放牧24头牛,则6天吃完牧草.若放牧21头牛,则8天吃完牧草.若每头牛每天吃草的量也都是相等的,设每头牛每天吃草的量为.问:
(1)放牧24头牛,6天所吃的牧草量用含,的代数式表示为______;放牧21头牛,8天所吃的牧草量用含,的代数式表示为______;
(2)试用表示,;
(3)若放牧16头牛,则几天可以吃完牧草?
19.一对夫妇现在年龄的和是其子女年龄和的6倍,这对夫妇两年前的年龄和是其子女两年前年龄和的10倍,6年后,这对夫妇的年龄和是其子女6年后年龄和的3倍,问这对夫妇共有多少个子女?
20.已知与的和仍是单项式,求、、的值.
参考答案
1.B
2.B
3.D
4.D
5.B
6.D
7.C
8.A
9.B
10.A
11.
12.
13.600
14.45%
15.
16.
17.(1);5;(2)购买5支铅笔、5块橡皮、5本日记本共需30元;(3).
【详解】
解:(1).
由①②可得:,
由①②可得:.
故答案为:;5.
(2)设铅笔的单价为元,橡皮的单价为元,日记本的单价为元,
依题意,得:,
由①②可得,
.
答:购买5支铅笔、5块橡皮、5本日记本共需30元.
(3)依题意,得:,
由①②可得:,
即.
故答案为:.
18.(1),;(2);(3)若放牧16头牛,18天可以吃完牧草.
【详解】
解:(1)放牧24头牛,6天所吃的牧草量为kg,放牧21头牛,8天所吃的牧草量为;
(2)由题意,得
解得
(3)设16头牛天可以吃完牧草,根据题意,得.
即.
解得.
答:若放牧16头牛,18天可以吃完牧草.
19.这对夫妇共有3个子女.
【解析】
试题分析:设这对夫妇的年龄的和为x,子女现在的年龄和为y,这对夫妇共有z个子女;根据本题中的三个等量关系为:此夫妇现在的年龄和=6×其子女现在的年龄和;此夫妇两年前的年龄和=10×其子女两年前的年龄和;此夫妇6年后的年龄和=3×其子女6年后的年龄和.可列出方程组,解方程组即可.
设现在这对夫妇的年龄和为x岁,子女现在的年龄和为y岁,这对夫妇共有z个子女,则
解得
答:这对夫妇共有3个子女.
20.
【详解】
根据题意可得,
解得:.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.有三种文具,每种价格分别是3元、7元和4元,现在有27元钱,三种文具都要买,恰好使钱用完的买法数有( )种.
A.1 B.2 C.3 D.4
2.下列四组数值中,方程组的解是( )
A. B. C. D.
3.方程组的解是( )
A. B. C. D.
4.已知如果x与y互为相反数,那么(???? )
A. B. C. D.
5.一套数学题集共有100道题,甲、乙和丙三人分别作答,每道题至少有一人解对,且每人都解对了其中的60道.如果将其中只有1人解对的题称作难题,2人解对的题称作中档题,3人都解对的题称作容易题,那么下列判断一定正确的是( )
A.容易题和中档题共60道 B.难题比容易题多20道
C.难题比中档题多10道 D.中档题比容易题多15道
6.在“自主互助学习型课堂竞赛”中,为奖励表现突出的同学,初一(7)班利用班费元钱,购买钢笔、相册、笔记本三种奖品,其中钢笔至多买支,若钢笔每支元,相册每本元,笔记本每本元,在把钱都用尽的条件下,买法共有( )
A.种 B.种 C.种 D.种
7.下列方程组中,是三元一次方程组的是( )
A. B. C. D.
8.在明代的《算法统宗》中记载了利用方格进行两数相乘的一种方法,叫做“铺地锦”,如图1,计算,将乘数47计入上行,乘数51计入右行,然后以乘数47的每位数字乘以乘数51的每位数字,将结果计入相应的格子中,最后按斜行加起来,得2397,图2用“铺地锦”法表示两个两位数相乘,则a的值为( )
A.7 B.5 C.3 D.2
9.甲,乙,丙三人共解出100道题,每人都解对其中的60道题,将其中只有1人解出的题叫做难题,2人解出叫做中等题,3人都解出的题叫做容易题,试问:难题和容易题谁多,多几题( )
A.容易题比难题多20题 B.难题比容易题多20题
C.一样多 D.无法确定
10.如果方程组的解使代数式kx+2y﹣3z的值为8,则k=( )
A. B.﹣ C.3 D.﹣3
二、填空题
11.当时,代数式的值是5;当时,代数式的值是0;当时,代数式的值是;则当时,代数式的值是_____.
12.某果蔬饮料由果汁、蔬菜汁和纯净水按一定质量比配制而成,纯净水、果汁、蔬菜汁的价格比为,因市场原因,果汁、蔬菜汁的价格涨了12.5%,而纯净水的价格降了20%,但并没有影响该饮料的成本(只考虑购买费用),那么该种饮料中果汁与蔬菜汁的质量和与纯净水的质量之比为______.
13.若,,…,是从0,,2这三个数中取值的一列数,若,,则,,…,中为2的个数是______.
14.某水稻种植中心培育了甲、乙、丙三种水稻,将这三种水稻分别种植于三块大小各不相同的试验田里.去年,三种水稻的平均亩产量分别为300kg,500kg,400kg,总平均亩产量为450kg,且丙种水稻的的总产量是甲种水稻总产量的4倍,今年初,研究人员改良了水稻种子,仍按去年的方式种植,三种水稻的平均亩产量都增加了.总平均亩产量增长了40%,甲、丙两种水稻的总产量增长了30%,则乙种水稻平均亩产量的增长率为_______.
15.在刚刚结束的万州二中秋季运动会中,有一个趣味项目,分钟内运送三大筐数量相同的兵乓球,甲每 次从第一个大筐中取出个球;乙每次从第二个大筐中取出个球;丙则是每次从第三个大筐中取出个 球.比赛激烈最终三人都记不清各自取了多少次球了,最后裁判清点发现第一个筐中剩下个球,第二个筐剩下个球,第三个筐剩下个球,那么根据上述情况可以推知每个筐中至少有____________个兵乓球.
16.已知x,y,z都不为0,且,则式子的值为_____.
三、解答题
17.阅读理解:已知实数x,y满足3x﹣y=5…①,2x+3y=7…②,求x﹣4y和7x+5y的值.仔细观察两个方程未知数的系数之间的关系,本题可以通过适当变形整体求得代数式的值,如由①﹣②可得x﹣4y=﹣2,由①+②×2可得7x+5y=19.这样的解题思想就是通常所说的“整体思想”.利用“整体思想”,解决下列问题:
(1)已知二元一次方程组?,则x﹣y= ,x+y= ;
(2)买20支铅笔、3块橡皮、2本日记本共需32元,买39支铅笔、5块橡皮、3本日记本共需58元,求购买5支铅笔、5块橡皮5本日记本共需多少元?
(3)对于实数x,y,定义新运算:x*y=ax+by+c,其中a,b,c是常数,等式右边是实数运算.已知3*5=15,4*7=28,求1*1的值.
18.有一片牧场原有的草量为,草每天都匀速地生长,这片牧场每天牧草的生长量都为.若在其上放牧24头牛,则6天吃完牧草.若放牧21头牛,则8天吃完牧草.若每头牛每天吃草的量也都是相等的,设每头牛每天吃草的量为.问:
(1)放牧24头牛,6天所吃的牧草量用含,的代数式表示为______;放牧21头牛,8天所吃的牧草量用含,的代数式表示为______;
(2)试用表示,;
(3)若放牧16头牛,则几天可以吃完牧草?
19.一对夫妇现在年龄的和是其子女年龄和的6倍,这对夫妇两年前的年龄和是其子女两年前年龄和的10倍,6年后,这对夫妇的年龄和是其子女6年后年龄和的3倍,问这对夫妇共有多少个子女?
20.已知与的和仍是单项式,求、、的值.
参考答案
1.B
2.B
3.D
4.D
5.B
6.D
7.C
8.A
9.B
10.A
11.
12.
13.600
14.45%
15.
16.
17.(1);5;(2)购买5支铅笔、5块橡皮、5本日记本共需30元;(3).
【详解】
解:(1).
由①②可得:,
由①②可得:.
故答案为:;5.
(2)设铅笔的单价为元,橡皮的单价为元,日记本的单价为元,
依题意,得:,
由①②可得,
.
答:购买5支铅笔、5块橡皮、5本日记本共需30元.
(3)依题意,得:,
由①②可得:,
即.
故答案为:.
18.(1),;(2);(3)若放牧16头牛,18天可以吃完牧草.
【详解】
解:(1)放牧24头牛,6天所吃的牧草量为kg,放牧21头牛,8天所吃的牧草量为;
(2)由题意,得
解得
(3)设16头牛天可以吃完牧草,根据题意,得.
即.
解得.
答:若放牧16头牛,18天可以吃完牧草.
19.这对夫妇共有3个子女.
【解析】
试题分析:设这对夫妇的年龄的和为x,子女现在的年龄和为y,这对夫妇共有z个子女;根据本题中的三个等量关系为:此夫妇现在的年龄和=6×其子女现在的年龄和;此夫妇两年前的年龄和=10×其子女两年前的年龄和;此夫妇6年后的年龄和=3×其子女6年后的年龄和.可列出方程组,解方程组即可.
设现在这对夫妇的年龄和为x岁,子女现在的年龄和为y岁,这对夫妇共有z个子女,则
解得
答:这对夫妇共有3个子女.
20.
【详解】
根据题意可得,
解得:.
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
