冀教版七年级下册7.2相交线课时训练(word版含答案)
文档属性
| 名称 | 冀教版七年级下册7.2相交线课时训练(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 312.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 17:05:30 | ||
图片预览

文档简介
7.2相交线课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列生活中的实例,可以用“两点之间线段最短”来解释的是( )
A.把一根木条固定到墙上需要两颗钉子
B.从一条河道能向集镇引一条最短的水渠
C.小狗看到远处的食物,总是径直奔向食物
D.经过刨平木板上的两个点,能弹出一条笔直的墨线
2.下列说法正确的个数是( )
①射线与射线是同一条射线;
②点到点的距离是线段;
③画一条长为的直线;
④在同一平面内,过一点有且只有一条直线垂直于已知直线.
A.0个 B.1个 C.2个 D.3个
3.如图,,,表示点到直线距离的是线段( )的长度
A. B. C. D.
4.北京大兴国际机场采用“三纵一横”全向型跑道构型,可节省飞机飞行时间,過极端天气侧向跑道可提升机场运行能力.跑道的布局为:三条南北向的跑道和一条偏东南走向的侧向跑道.如图,侧向跑道在点南偏东70°的方向上,则这条跑道所在射线与正北方向所成角的度数为( )
A.160° B.110° C.70° D.20°
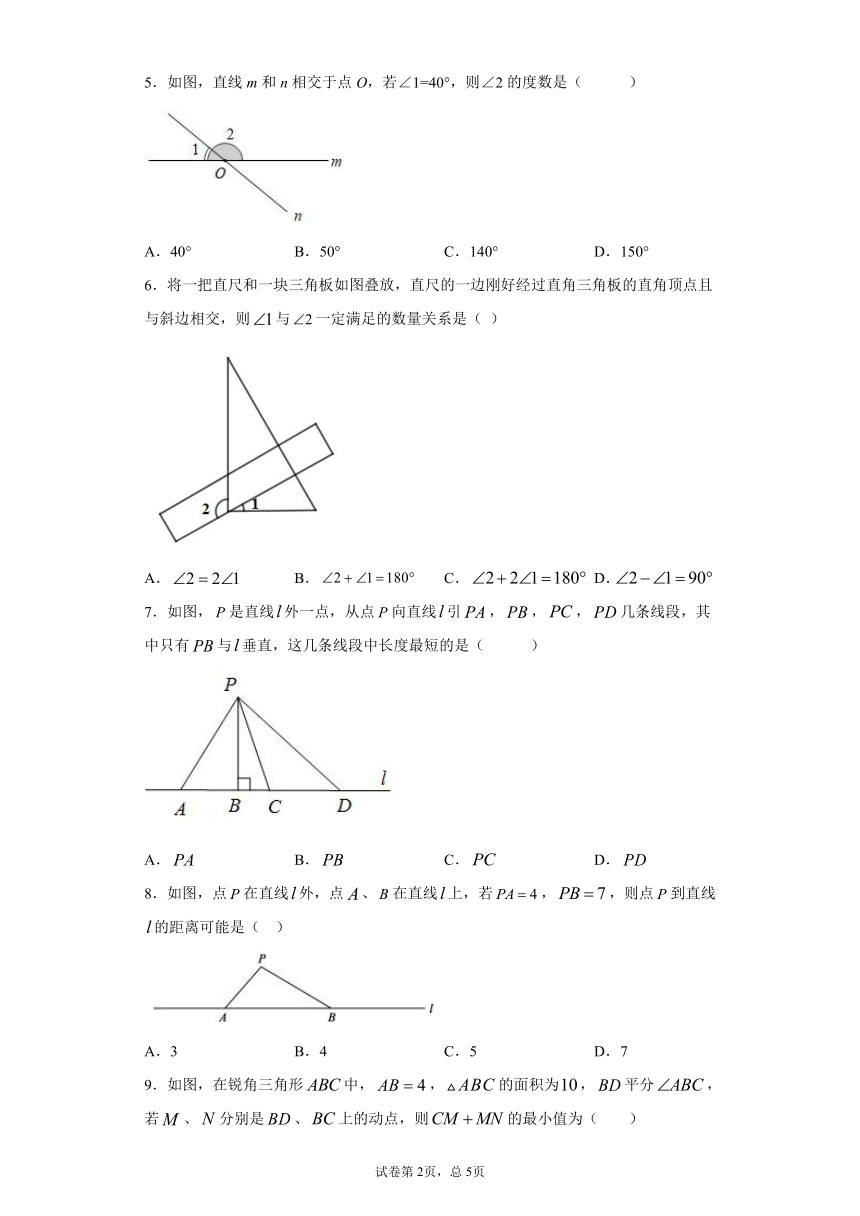
5.如图,直线m和n相交于点O,若∠1=40°,则∠2的度数是( )
A.40° B.50° C.140° D.150°
6.将一把直尺和一块三角板如图叠放,直尺的一边刚好经过直角三角板的直角顶点且与斜边相交,则与一定满足的数量关系是( )
A. B. C. D.
7.如图,是直线外一点,从点向直线引,,,几条线段,其中只有与垂直,这几条线段中长度最短的是( )
A. B. C. D.
8.如图,点在直线外,点、在直线上,若,,则点到直线的距离可能是( )
A.3 B.4 C.5 D.7
9.如图,在锐角三角形中,,的面积为,平分,若、分别是、上的动点,则的最小值为( )
A. B. C. D.
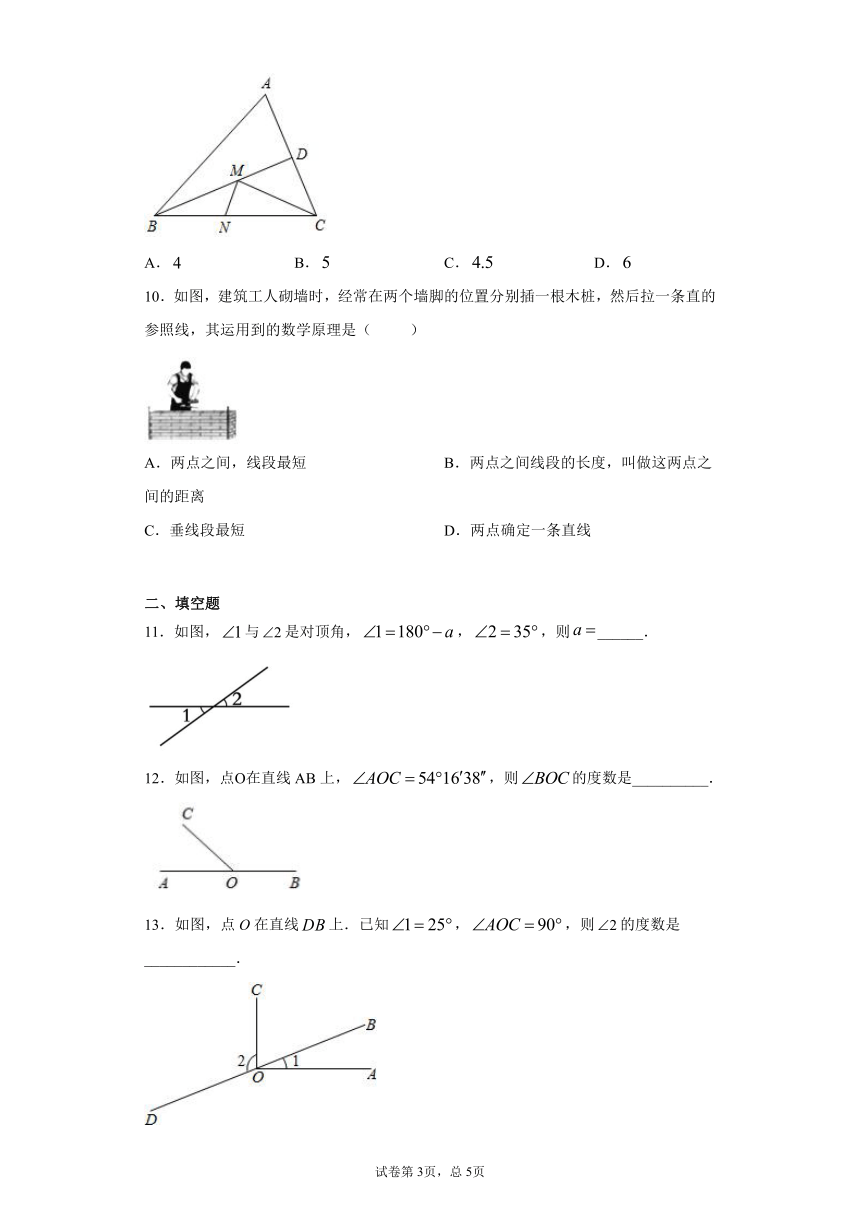
10.如图,建筑工人砌墙时,经常在两个墙脚的位置分别插一根木桩,然后拉一条直的参照线,其运用到的数学原理是( )
A.两点之间,线段最短 B.两点之间线段的长度,叫做这两点之间的距离
C.垂线段最短 D.两点确定一条直线
二、填空题
11.如图,与是对顶角,,,则______.
12.如图,点О在直线AB上,,则的度数是__________.
13.如图,点O在直线上.已知,,则的度数是____________.
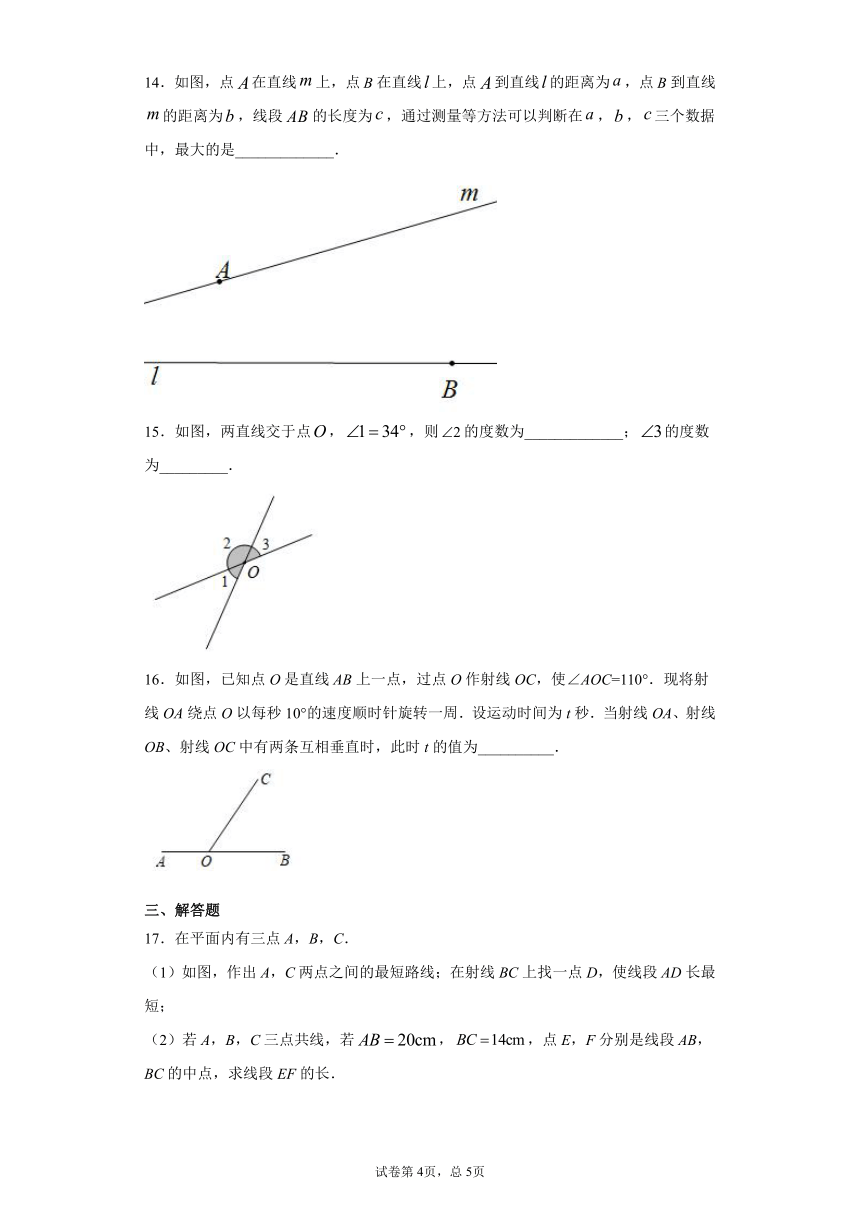
14.如图,点在直线上,点在直线上,点到直线的距离为,点到直线的距离为,线段的长度为,通过测量等方法可以判断在,,三个数据中,最大的是_____________.
15.如图,两直线交于点,,则的度数为_____________;的度数为_________.
16.如图,已知点O是直线AB上一点,过点O作射线OC,使∠AOC=110°.现将射线OA绕点O以每秒10°的速度顺时针旋转一周.设运动时间为t秒.当射线OA、射线OB、射线OC中有两条互相垂直时,此时t的值为__________.
三、解答题
17.在平面内有三点A,B,C.
(1)如图,作出A,C两点之间的最短路线;在射线BC上找一点D,使线段AD长最短;
(2)若A,B,C三点共线,若,,点E,F分别是线段AB,BC的中点,求线段EF的长.
18.如图,直线AB与CD相交于点O,.
(1)如果,求和的度数.
(2)如果,求的度数.
19.如图,直线、相交于点,,.若是的平分线,求的度数.
20.如图,直线、相交于点,平分,平分,.
(1)求的度数;
(2)求的度数.
参考答案
1.C
2.B
3.B
4.B
5.C
6.D
7.B
8.A
9.B
10.D
11.145°
12.
13.115°
14.
15.
16.2、9、20或27
17.(1)图见解析;(2)线段EF的长为或.
【详解】
解:(1)连接AC,线段AC即为A,C之间最短路线,
过A作AD⊥BC,AD即为最短;
(2)①如下图,若A、B、C按顺序排列,
∵E、F分别是线段AB,BC的中点,,,
∴,
∴,
②若C在AB中间,如下图,
∵E、F分别是线段AB,BC的中点,,,
∴,
.
综上所述,线段EF的长为或.
18.(1)70°,20°;(2)150°
【详解】
解:(1),,
,;
(2)设,则,
,
即,
解得,,
,
.
19.45°
【详解】
解:∵
∴
∵平分
∴∠1=∠2=
又∵
∴
∴∠2+∠3=
∴.
20.(1)30°,(2)45°.
【详解】
解:(1)∵,∠AOD+∠BOD=180°,
∴∠BOD=×180°=60°,
∵OE平分∠BOD,
∴∠DOE=∠BOE=∠BOD=×60°=30°;
(2)∠COE=∠COD﹣∠DOE=180°﹣30°=150°,
∵OF平分∠COE,
∴∠EOF=∠COE=×150°=75°,
由(1)得,∠BOE=30°,
∴∠BOF=∠EOF-∠BOE=75°-30°=45°.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列生活中的实例,可以用“两点之间线段最短”来解释的是( )
A.把一根木条固定到墙上需要两颗钉子
B.从一条河道能向集镇引一条最短的水渠
C.小狗看到远处的食物,总是径直奔向食物
D.经过刨平木板上的两个点,能弹出一条笔直的墨线
2.下列说法正确的个数是( )
①射线与射线是同一条射线;
②点到点的距离是线段;
③画一条长为的直线;
④在同一平面内,过一点有且只有一条直线垂直于已知直线.
A.0个 B.1个 C.2个 D.3个
3.如图,,,表示点到直线距离的是线段( )的长度
A. B. C. D.
4.北京大兴国际机场采用“三纵一横”全向型跑道构型,可节省飞机飞行时间,過极端天气侧向跑道可提升机场运行能力.跑道的布局为:三条南北向的跑道和一条偏东南走向的侧向跑道.如图,侧向跑道在点南偏东70°的方向上,则这条跑道所在射线与正北方向所成角的度数为( )
A.160° B.110° C.70° D.20°
5.如图,直线m和n相交于点O,若∠1=40°,则∠2的度数是( )
A.40° B.50° C.140° D.150°
6.将一把直尺和一块三角板如图叠放,直尺的一边刚好经过直角三角板的直角顶点且与斜边相交,则与一定满足的数量关系是( )
A. B. C. D.
7.如图,是直线外一点,从点向直线引,,,几条线段,其中只有与垂直,这几条线段中长度最短的是( )
A. B. C. D.
8.如图,点在直线外,点、在直线上,若,,则点到直线的距离可能是( )
A.3 B.4 C.5 D.7
9.如图,在锐角三角形中,,的面积为,平分,若、分别是、上的动点,则的最小值为( )
A. B. C. D.
10.如图,建筑工人砌墙时,经常在两个墙脚的位置分别插一根木桩,然后拉一条直的参照线,其运用到的数学原理是( )
A.两点之间,线段最短 B.两点之间线段的长度,叫做这两点之间的距离
C.垂线段最短 D.两点确定一条直线
二、填空题
11.如图,与是对顶角,,,则______.
12.如图,点О在直线AB上,,则的度数是__________.
13.如图,点O在直线上.已知,,则的度数是____________.
14.如图,点在直线上,点在直线上,点到直线的距离为,点到直线的距离为,线段的长度为,通过测量等方法可以判断在,,三个数据中,最大的是_____________.
15.如图,两直线交于点,,则的度数为_____________;的度数为_________.
16.如图,已知点O是直线AB上一点,过点O作射线OC,使∠AOC=110°.现将射线OA绕点O以每秒10°的速度顺时针旋转一周.设运动时间为t秒.当射线OA、射线OB、射线OC中有两条互相垂直时,此时t的值为__________.
三、解答题
17.在平面内有三点A,B,C.
(1)如图,作出A,C两点之间的最短路线;在射线BC上找一点D,使线段AD长最短;
(2)若A,B,C三点共线,若,,点E,F分别是线段AB,BC的中点,求线段EF的长.
18.如图,直线AB与CD相交于点O,.
(1)如果,求和的度数.
(2)如果,求的度数.
19.如图,直线、相交于点,,.若是的平分线,求的度数.
20.如图,直线、相交于点,平分,平分,.
(1)求的度数;
(2)求的度数.
参考答案
1.C
2.B
3.B
4.B
5.C
6.D
7.B
8.A
9.B
10.D
11.145°
12.
13.115°
14.
15.
16.2、9、20或27
17.(1)图见解析;(2)线段EF的长为或.
【详解】
解:(1)连接AC,线段AC即为A,C之间最短路线,
过A作AD⊥BC,AD即为最短;
(2)①如下图,若A、B、C按顺序排列,
∵E、F分别是线段AB,BC的中点,,,
∴,
∴,
②若C在AB中间,如下图,
∵E、F分别是线段AB,BC的中点,,,
∴,
.
综上所述,线段EF的长为或.
18.(1)70°,20°;(2)150°
【详解】
解:(1),,
,;
(2)设,则,
,
即,
解得,,
,
.
19.45°
【详解】
解:∵
∴
∵平分
∴∠1=∠2=
又∵
∴
∴∠2+∠3=
∴.
20.(1)30°,(2)45°.
【详解】
解:(1)∵,∠AOD+∠BOD=180°,
∴∠BOD=×180°=60°,
∵OE平分∠BOD,
∴∠DOE=∠BOE=∠BOD=×60°=30°;
(2)∠COE=∠COD﹣∠DOE=180°﹣30°=150°,
∵OF平分∠COE,
∴∠EOF=∠COE=×150°=75°,
由(1)得,∠BOE=30°,
∴∠BOF=∠EOF-∠BOE=75°-30°=45°.
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
