冀教版七年级下册7.4平行线的判定课时训练(word版含答案)
文档属性
| 名称 | 冀教版七年级下册7.4平行线的判定课时训练(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 291.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 16:56:44 | ||
图片预览



文档简介
7.4平行线的判定课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,“因为,所以”,其推导的依据是( )
A.两直线平行,同位角相等 B.两直线平行,内错角相等
C.同位角相等,两直线平行 D.内错角相等,两直线平行
2.如图,下列四个图中,不能判断不能判定的是( )
A. B. C. D.
3.如图所示,下列四组条件中,能得到AB//CD的是( )
A.∠1=∠2 B.∠BAD=∠BCD
C.∠ABC=∠ADC,∠2=∠3 D.∠BAD+∠ABC=180°
4.如图,直线a、b被直线c所截,下列条件不能判定直线a与b平行的是( )
A.∠1=∠3 B.∠2+∠4=180° C.∠1=∠4 D.∠1+∠4=180°
5.如图,在下列给出的条件中,能判定的是( )
A.∠4=∠3 B.∠1=∠A C.∠1=∠4 D.∠4+∠2=180°
6.如图,能判断直线AB∥CD的条件是( )
A. B. C. D.
7.如图,已知直线a、b、c,若∠1=∠2=60°,且∠2=∠3,则图中平行线组数为( )
A.0 B.1 C.2 D.3
8.如图,可以判定的条件是( )
A. B. C. D.
9.如图,直线a,b被直线c所截,现给出下列四个条件:(1);(2);(3);(4),其中能判定的条件的序号是( )
A.(1),(2) B.(1),(3) C.(1),(4) D.(3),(4)
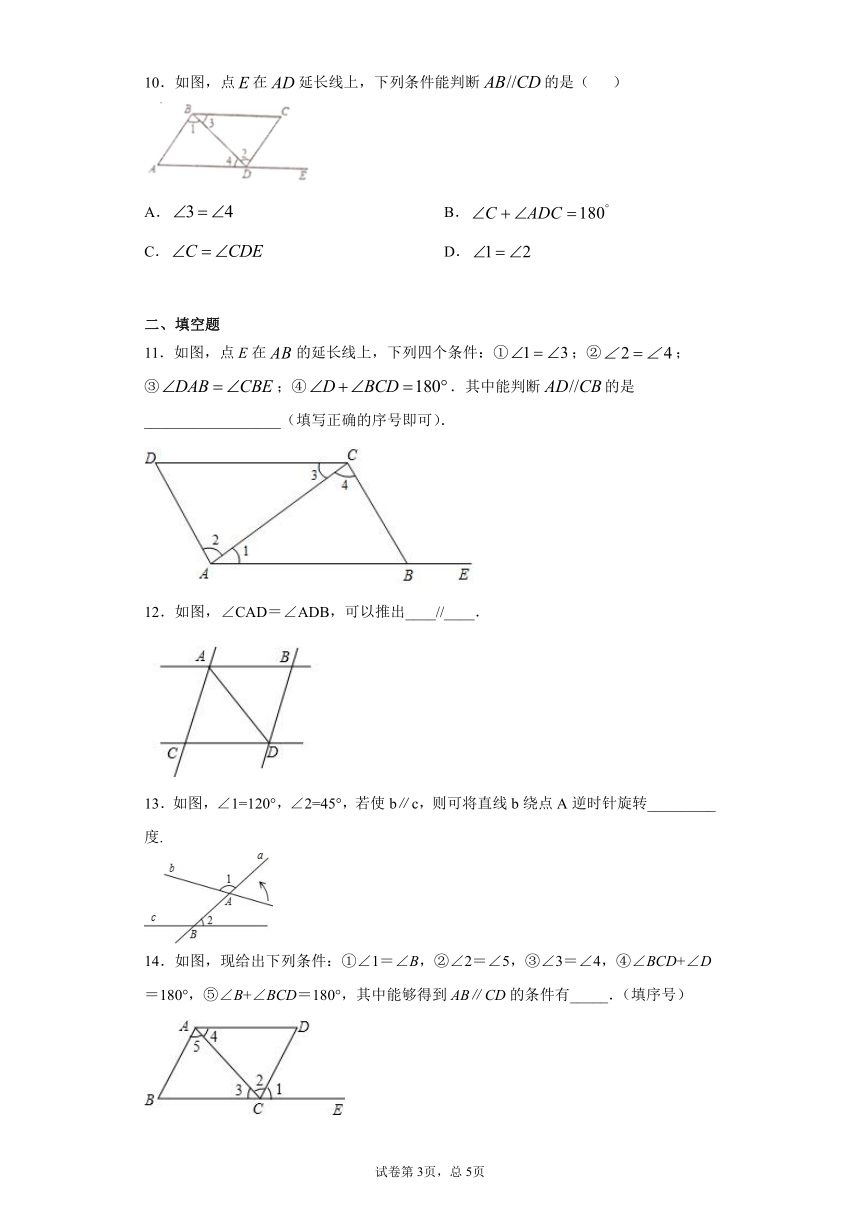
10.如图,点在延长线上,下列条件能判断的是( )
A. B.
C. D.
二、填空题
11.如图,点E在的延长线上,下列四个条件:①;②;③;④.其中能判断的是__________________(填写正确的序号即可).
12.如图,∠CAD=∠ADB,可以推出____//____.
13.如图,∠1=120°,∠2=45°,若使b∥c,则可将直线b绕点A逆时针旋转_________度.
14.如图,现给出下列条件:①∠1=∠B,②∠2=∠5,③∠3=∠4,④∠BCD+∠D=180°,⑤∠B+∠BCD=180°,其中能够得到AB∥CD的条件有_____.(填序号)
15.如图,不添加辅助线,请写出一个能判定∥的条件___________.
16.命题“在同一平面内,如果,那么”是________命题.(填“真”或“假”)
三、解答题
17.如图,已知平分,点D在射线上,且.判断与的位置关系,并说明理由.
18.如图所示:
(1)若,,,求证:.
(2)若把(1)中的题设“”与结论“”对调,所得命题是否是真命题?说明理由.
19.如图①,在三角形ABC中,点E,F分别为线段AB,AC上任意两点,EG交BC于点G,交AC的延长线于点H,∠1+∠AFE=180°.
(1)证明:BC∥EF;
(2)如图②,若∠2=∠3,∠BEG=∠EDF,证明:DF平分∠AFE.
20.如图,,那么直线与平行吗?为什么?
参考答案
1.D
2.C
3.C
4.D
5.C
6.A
7.D
8.C
9.A
10.D
11.②③④
12.AC BD
13.15
14.①②⑤
15.
16.假
17.BC∥DE;理由见解析
【详解】
解:BC∥DE;理由如下:
因为平分,
所以∠ABE=∠CBE,
因为,
所以∠CBE=∠BED,
所以BC∥DE.
18.(1)详见解析;(2)是真命题.
【详解】
解:(1)证明:(已知),
.(两直线平行,内错角相等),
(已知),
(等量代换),
.(同位角相等,两直线平行),
.(两直线平行,同位角相等),
.(垂直的定义);
(2)是真命题,理由如下:
(已知),
,
.(同位角相等,两直线平行),
.(两直线平行,同位角相等),
(已知),
.(等量代换),
.(内错角相等,两直线平行).
19.(1)见解析;(2) 见解析.
【详解】
证明:(1)∵∠1+∠AFE=180°,∠1+∠BCF=180°,
∴∠AFE=∠BCF,
∴BC∥EF;
(2)∵∠BEG=∠EDF,
∴DF∥EH,
∴∠DFE=∠FEH,
又∵BC∥EF,
∴∠FEH=∠2,
又∵∠2=∠3,
∴∠DFE=∠3,
∴DF平分∠AFE.
20.,理由详见解析
【详解】
解:
理由:
又
又
(同位角相等,两直线平行).
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,“因为,所以”,其推导的依据是( )
A.两直线平行,同位角相等 B.两直线平行,内错角相等
C.同位角相等,两直线平行 D.内错角相等,两直线平行
2.如图,下列四个图中,不能判断不能判定的是( )
A. B. C. D.
3.如图所示,下列四组条件中,能得到AB//CD的是( )
A.∠1=∠2 B.∠BAD=∠BCD
C.∠ABC=∠ADC,∠2=∠3 D.∠BAD+∠ABC=180°
4.如图,直线a、b被直线c所截,下列条件不能判定直线a与b平行的是( )
A.∠1=∠3 B.∠2+∠4=180° C.∠1=∠4 D.∠1+∠4=180°
5.如图,在下列给出的条件中,能判定的是( )
A.∠4=∠3 B.∠1=∠A C.∠1=∠4 D.∠4+∠2=180°
6.如图,能判断直线AB∥CD的条件是( )
A. B. C. D.
7.如图,已知直线a、b、c,若∠1=∠2=60°,且∠2=∠3,则图中平行线组数为( )
A.0 B.1 C.2 D.3
8.如图,可以判定的条件是( )
A. B. C. D.
9.如图,直线a,b被直线c所截,现给出下列四个条件:(1);(2);(3);(4),其中能判定的条件的序号是( )
A.(1),(2) B.(1),(3) C.(1),(4) D.(3),(4)
10.如图,点在延长线上,下列条件能判断的是( )
A. B.
C. D.
二、填空题
11.如图,点E在的延长线上,下列四个条件:①;②;③;④.其中能判断的是__________________(填写正确的序号即可).
12.如图,∠CAD=∠ADB,可以推出____//____.
13.如图,∠1=120°,∠2=45°,若使b∥c,则可将直线b绕点A逆时针旋转_________度.
14.如图,现给出下列条件:①∠1=∠B,②∠2=∠5,③∠3=∠4,④∠BCD+∠D=180°,⑤∠B+∠BCD=180°,其中能够得到AB∥CD的条件有_____.(填序号)
15.如图,不添加辅助线,请写出一个能判定∥的条件___________.
16.命题“在同一平面内,如果,那么”是________命题.(填“真”或“假”)
三、解答题
17.如图,已知平分,点D在射线上,且.判断与的位置关系,并说明理由.
18.如图所示:
(1)若,,,求证:.
(2)若把(1)中的题设“”与结论“”对调,所得命题是否是真命题?说明理由.
19.如图①,在三角形ABC中,点E,F分别为线段AB,AC上任意两点,EG交BC于点G,交AC的延长线于点H,∠1+∠AFE=180°.
(1)证明:BC∥EF;
(2)如图②,若∠2=∠3,∠BEG=∠EDF,证明:DF平分∠AFE.
20.如图,,那么直线与平行吗?为什么?
参考答案
1.D
2.C
3.C
4.D
5.C
6.A
7.D
8.C
9.A
10.D
11.②③④
12.AC BD
13.15
14.①②⑤
15.
16.假
17.BC∥DE;理由见解析
【详解】
解:BC∥DE;理由如下:
因为平分,
所以∠ABE=∠CBE,
因为,
所以∠CBE=∠BED,
所以BC∥DE.
18.(1)详见解析;(2)是真命题.
【详解】
解:(1)证明:(已知),
.(两直线平行,内错角相等),
(已知),
(等量代换),
.(同位角相等,两直线平行),
.(两直线平行,同位角相等),
.(垂直的定义);
(2)是真命题,理由如下:
(已知),
,
.(同位角相等,两直线平行),
.(两直线平行,同位角相等),
(已知),
.(等量代换),
.(内错角相等,两直线平行).
19.(1)见解析;(2) 见解析.
【详解】
证明:(1)∵∠1+∠AFE=180°,∠1+∠BCF=180°,
∴∠AFE=∠BCF,
∴BC∥EF;
(2)∵∠BEG=∠EDF,
∴DF∥EH,
∴∠DFE=∠FEH,
又∵BC∥EF,
∴∠FEH=∠2,
又∵∠2=∠3,
∴∠DFE=∠3,
∴DF平分∠AFE.
20.,理由详见解析
【详解】
解:
理由:
又
又
(同位角相等,两直线平行).
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
