冀教版八年级下册22.1平行四边形的性质同步课时训练(word版,含答案)
文档属性
| 名称 | 冀教版八年级下册22.1平行四边形的性质同步课时训练(word版,含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 412.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 00:00:00 | ||
图片预览



文档简介
22.1平行四边形的性质同步课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在中,,将绕点逆时针旋转得到,且,设旋转角为,则的大小为( )
A.30° B.45° C.60° D.75°
2.如图1,平行四边形纸片的面积为120,.今沿两对角线将四边形剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(、重合)形成一轴对称图形(戊),如图2所示,则图形戊的两对角线长度和为( )
A.26 B.29 C. D.
3.如图,在平行四边形中,平分,,,则平行四边形的周长是( )
A.16 B.14 C.20 D.24
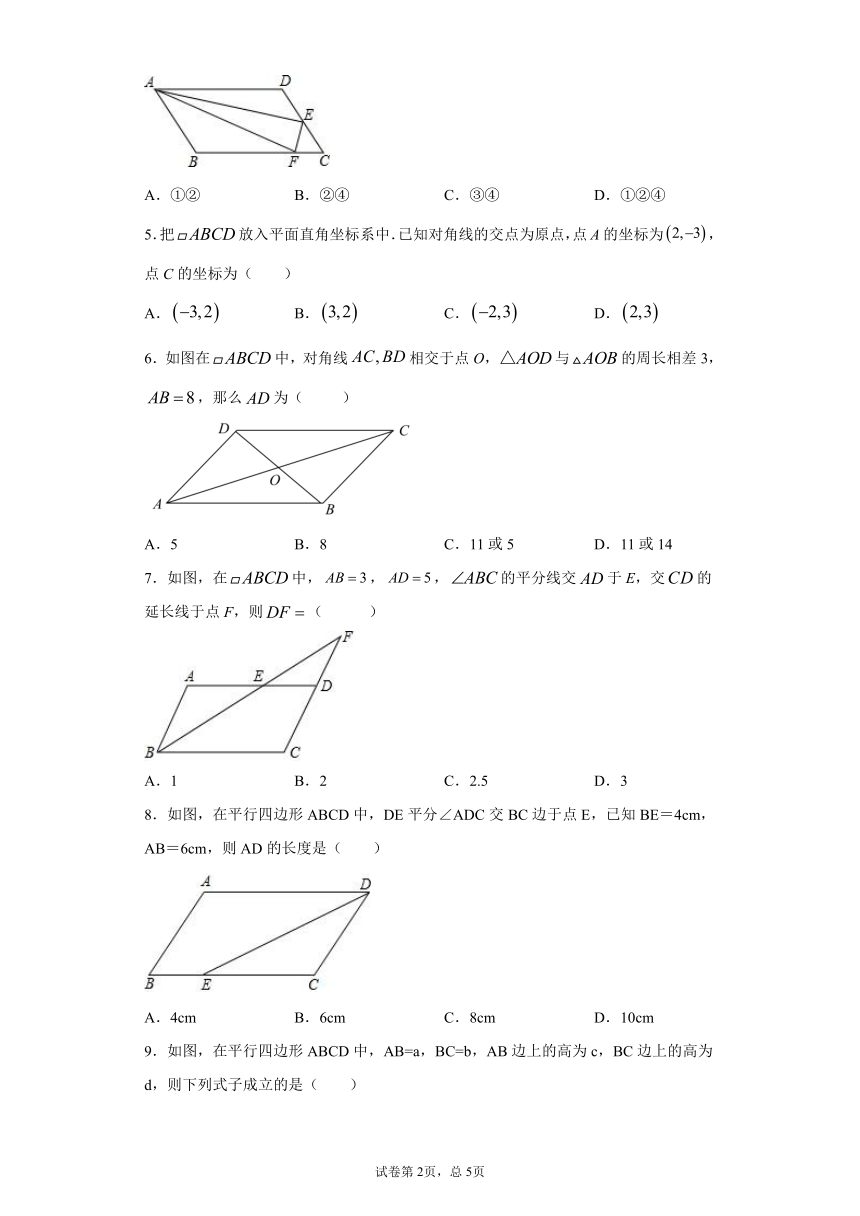
4.在中.是上一点,平分,且是的中点,则下列结论:①;②;③;④,其中正确的是( )
A.①② B.②④ C.③④ D.①②④
5.把放入平面直角坐标系中.已知对角线的交点为原点,点A的坐标为,点C的坐标为( )
A. B. C. D.
6.如图在中,对角线相交于点O,与的周长相差3,,那么为( )
A.5 B.8 C.11或5 D.11或14
7.如图,在中,,,的平分线交于E,交的延长线于点F,则( )
A.1 B.2 C.2.5 D.3
8.如图,在平行四边形ABCD中,DE平分∠ADC交BC边于点E,已知BE=4cm,AB=6cm,则AD的长度是( )
A.4cm B.6cm C.8cm D.10cm
9.如图,在平行四边形ABCD中,AB=a,BC=b,AB边上的高为c,BC边上的高为d,则下列式子成立的是( )
A.a:c=b:d B.a:b=c:d C.ab=cd D.ac=bd
10.如图,在平行四边形中,点是对角线的中点,过点作线段,使点,点分别在边,上(不与四边形顶点重合),连结,.设,下列结论:①若,则;②若,则与面积相等;③若,则.其中正确的是( )
A.① B.② C.③ D.②③
二、填空题
11.如图,过对角线的交点,交于,交于,若的周长为19,,则四边形的周长为_____.
12.如图,将沿对角线进行折叠,折叠后点D落在点F处,交于点E,有下列结论:①;②;③;④,其中正确结论的是__________.
13.如图,是的对角线,点在上,,,则的度数是______.
14.如图,在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=8,EF=1,则BC长为__________.
15.如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且DN=,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=______.
16.如图,在中,,,,点是边上一动点,以为对角线的所有平行四边形中,对角线最小的值是_____.
三、解答题
17.如图,在中,?分别是和的角平分线,已知.
(1)求线段的长;
(2)延长,交的延长线于点Q.
①请在答卷上补全图形;
②若,求的周长.
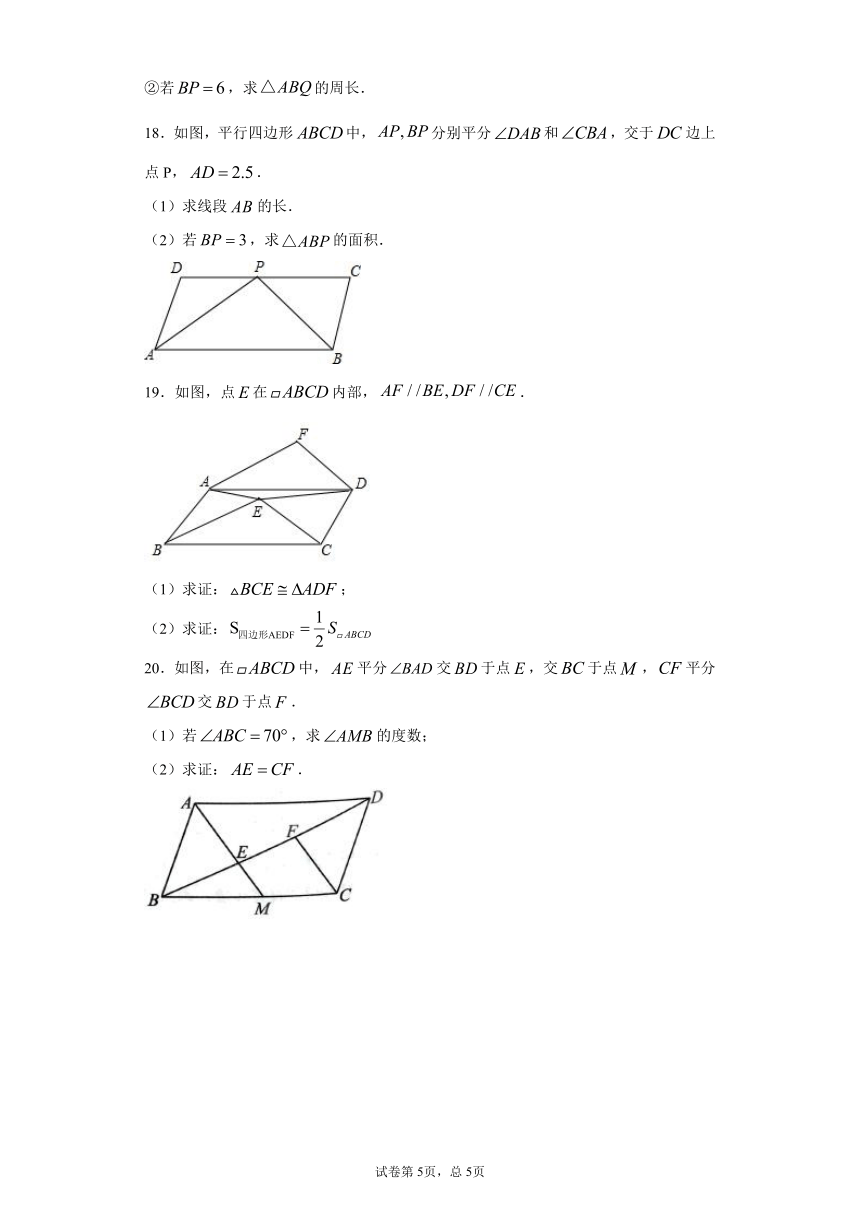
18.如图,平行四边形中,分别平分和,交于边上点P,.
(1)求线段的长.
(2)若,求的面积.
19.如图,点在内部,.
(1)求证:;
(2)求证:
20.如图,在中,平分交于点,交于点,平分交于点.
(1)若,求的度数;
(2)求证:.
参考答案
1.A
2.A
3.C
4.C
5.C
6.C
7.B
8.D
9.D
10.B
11.14.5
12.①②③
13.
14.15
15.
16.
17.(1)10;(2)①见解析;②36
【详解】
解:(1)∵在□ABCD中,AD=5,
∴BC=5,
∵AB∥CD,
∴∠BAP=∠DPA,
∵AP平分∠BAD,
∴∠BAP=∠DAP,
∴∠DAP=∠DPA,
∴DP=AD=5,
同理可得,CP=BC=5,
∴CD=10,
∴AB=10;
(2)①如图所示:
②∵AD∥BQ,
∴∠Q=∠DAP,
又∵∠DAP=∠BAP,
∴∠Q=∠BAP,
∴AB=QB=10,
又∵BP平分∠ABQ,
∴BP⊥AQ,AP=QP,
∴Rt△ABP中,AP==8,
∴AQ=16,
∴△ABQ的周长为:16+10+10=36.
18.(1)5;(2)6
【详解】
解:(1)∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵四边形ABCD是平行四边形,
∵AB∥CD,
∴∠PAB=∠DPA
∴∠DAP=∠DPA
∴△ADP是等腰三角形,
∴AD=DP=2.5,
同理:PC=CB=2.5,
即AB=DC=DP+PC=5;
(2)∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA=(∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°-(∠PAB+∠PBA)=90°;
在Rt△APB中,AB=5,BP=3,
∴AP==4,
∴△APB的面积=4×3÷2=6.
19.(1)见解析;(2)见解析
【详解】
解:四边形是平行四边形,
,
同理得
点在内部,
∴,
由知:
∴.
20.(1)55°;(2)见解析
【详解】
(1)解:∵四边形是平行四边形,
∴,
∴ .
∵,
∴.
∵平分,
∴.
∵,
∴.
(2)证明:∵四边形是平行四边形,
∴,,,
∴ .
∵平分,
∴.
∵平分,
∴.
∵,
∴.
又∵,,
∴,
∴.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在中,,将绕点逆时针旋转得到,且,设旋转角为,则的大小为( )
A.30° B.45° C.60° D.75°
2.如图1,平行四边形纸片的面积为120,.今沿两对角线将四边形剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(、重合)形成一轴对称图形(戊),如图2所示,则图形戊的两对角线长度和为( )
A.26 B.29 C. D.
3.如图,在平行四边形中,平分,,,则平行四边形的周长是( )
A.16 B.14 C.20 D.24
4.在中.是上一点,平分,且是的中点,则下列结论:①;②;③;④,其中正确的是( )
A.①② B.②④ C.③④ D.①②④
5.把放入平面直角坐标系中.已知对角线的交点为原点,点A的坐标为,点C的坐标为( )
A. B. C. D.
6.如图在中,对角线相交于点O,与的周长相差3,,那么为( )
A.5 B.8 C.11或5 D.11或14
7.如图,在中,,,的平分线交于E,交的延长线于点F,则( )
A.1 B.2 C.2.5 D.3
8.如图,在平行四边形ABCD中,DE平分∠ADC交BC边于点E,已知BE=4cm,AB=6cm,则AD的长度是( )
A.4cm B.6cm C.8cm D.10cm
9.如图,在平行四边形ABCD中,AB=a,BC=b,AB边上的高为c,BC边上的高为d,则下列式子成立的是( )
A.a:c=b:d B.a:b=c:d C.ab=cd D.ac=bd
10.如图,在平行四边形中,点是对角线的中点,过点作线段,使点,点分别在边,上(不与四边形顶点重合),连结,.设,下列结论:①若,则;②若,则与面积相等;③若,则.其中正确的是( )
A.① B.② C.③ D.②③
二、填空题
11.如图,过对角线的交点,交于,交于,若的周长为19,,则四边形的周长为_____.
12.如图,将沿对角线进行折叠,折叠后点D落在点F处,交于点E,有下列结论:①;②;③;④,其中正确结论的是__________.
13.如图,是的对角线,点在上,,,则的度数是______.
14.如图,在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=8,EF=1,则BC长为__________.
15.如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且DN=,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=______.
16.如图,在中,,,,点是边上一动点,以为对角线的所有平行四边形中,对角线最小的值是_____.
三、解答题
17.如图,在中,?分别是和的角平分线,已知.
(1)求线段的长;
(2)延长,交的延长线于点Q.
①请在答卷上补全图形;
②若,求的周长.
18.如图,平行四边形中,分别平分和,交于边上点P,.
(1)求线段的长.
(2)若,求的面积.
19.如图,点在内部,.
(1)求证:;
(2)求证:
20.如图,在中,平分交于点,交于点,平分交于点.
(1)若,求的度数;
(2)求证:.
参考答案
1.A
2.A
3.C
4.C
5.C
6.C
7.B
8.D
9.D
10.B
11.14.5
12.①②③
13.
14.15
15.
16.
17.(1)10;(2)①见解析;②36
【详解】
解:(1)∵在□ABCD中,AD=5,
∴BC=5,
∵AB∥CD,
∴∠BAP=∠DPA,
∵AP平分∠BAD,
∴∠BAP=∠DAP,
∴∠DAP=∠DPA,
∴DP=AD=5,
同理可得,CP=BC=5,
∴CD=10,
∴AB=10;
(2)①如图所示:
②∵AD∥BQ,
∴∠Q=∠DAP,
又∵∠DAP=∠BAP,
∴∠Q=∠BAP,
∴AB=QB=10,
又∵BP平分∠ABQ,
∴BP⊥AQ,AP=QP,
∴Rt△ABP中,AP==8,
∴AQ=16,
∴△ABQ的周长为:16+10+10=36.
18.(1)5;(2)6
【详解】
解:(1)∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵四边形ABCD是平行四边形,
∵AB∥CD,
∴∠PAB=∠DPA
∴∠DAP=∠DPA
∴△ADP是等腰三角形,
∴AD=DP=2.5,
同理:PC=CB=2.5,
即AB=DC=DP+PC=5;
(2)∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA=(∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°-(∠PAB+∠PBA)=90°;
在Rt△APB中,AB=5,BP=3,
∴AP==4,
∴△APB的面积=4×3÷2=6.
19.(1)见解析;(2)见解析
【详解】
解:四边形是平行四边形,
,
同理得
点在内部,
∴,
由知:
∴.
20.(1)55°;(2)见解析
【详解】
(1)解:∵四边形是平行四边形,
∴,
∴ .
∵,
∴.
∵平分,
∴.
∵,
∴.
(2)证明:∵四边形是平行四边形,
∴,,,
∴ .
∵平分,
∴.
∵平分,
∴.
∵,
∴.
又∵,,
∴,
∴.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
