冀教版八年级下册22.4矩形同步课时训练(Word版 含答案)
文档属性
| 名称 | 冀教版八年级下册22.4矩形同步课时训练(Word版 含答案) |

|
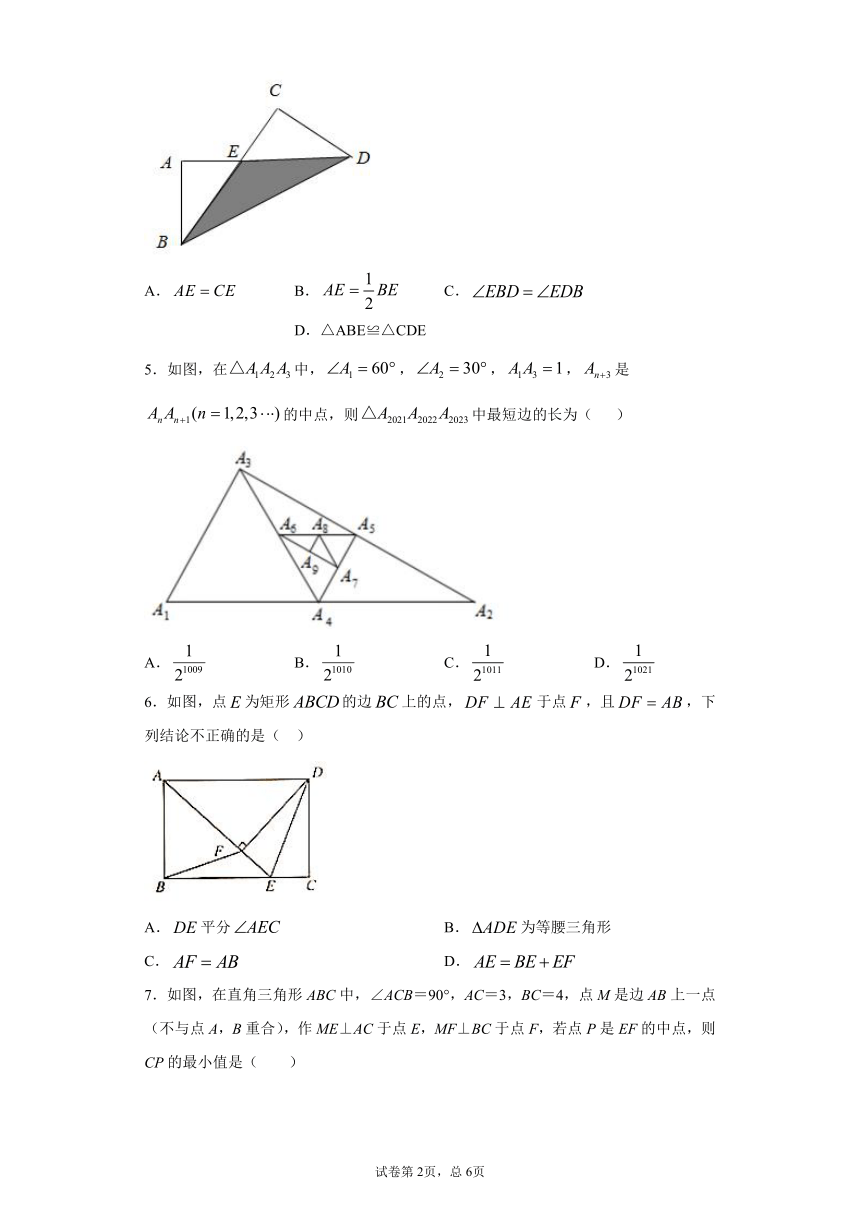
|
| 格式 | docx | ||
| 文件大小 | 440.1KB | ||
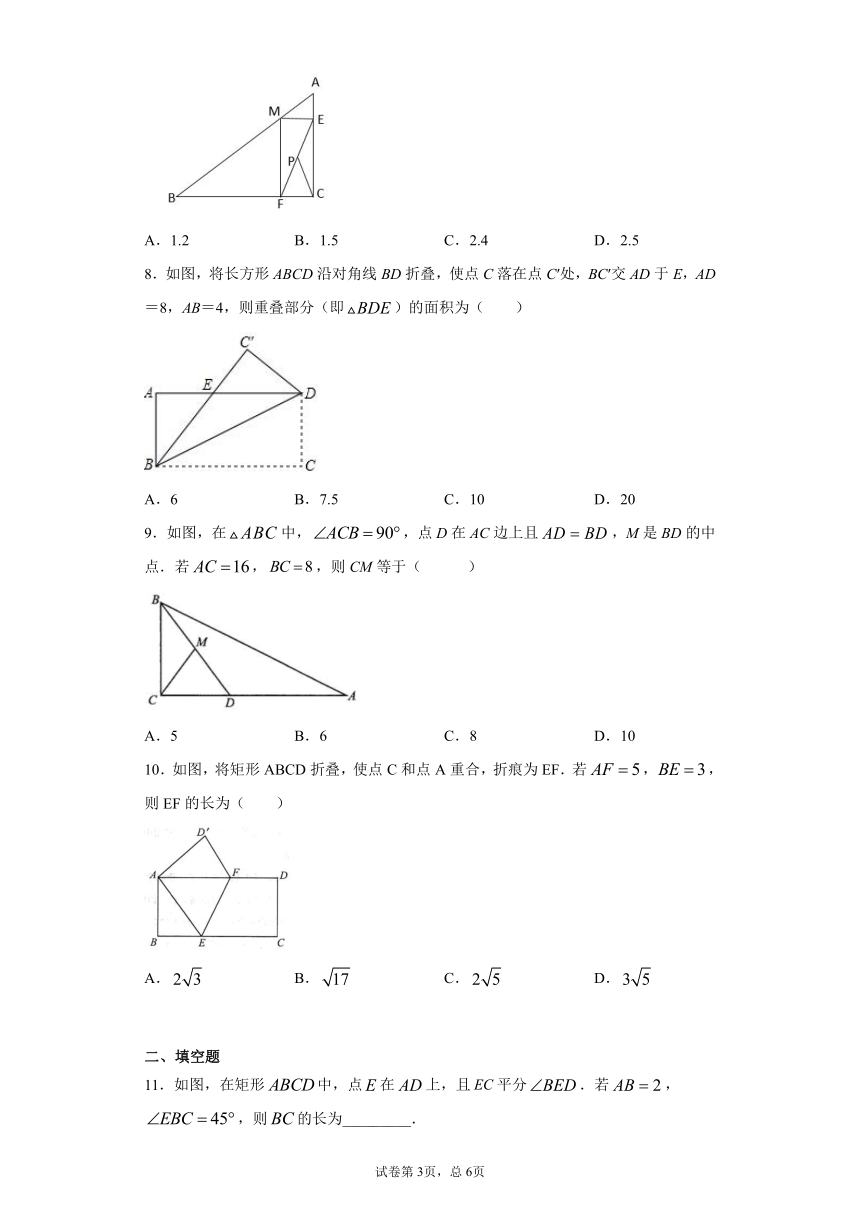
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 00:00:00 | ||
图片预览



文档简介
22.4矩形同步课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在长方形ABCD中,AE平分∠BAD交BC于点E,连接ED,若ED=5,EC=3,则长方形的周长为( )
A.20 B.22 C.24 D.26
2.如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于点G,CDAE.若BD6,CD5,则△DCG的面积是( )
A.10 B.5 C. D.
3.如图,在矩形中,点,分别在边,上,且,将矩形沿直线折叠,使点恰好落在边上的点处,则的长为( )
A.9 B.8 C. D.
4.如图,把长方形纸片沿对角线折叠,设重叠部分为.下列说法错误的是( )
A. B. C. D.△ABE≌△CDE
5.如图,在中,,,,是的中点,则中最短边的长为( )
A. B. C. D.
6.如图,点为矩形的边上的点,于点,且,下列结论不正确的是( )
A.平分 B.为等腰三角形
C. D.
7.如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则CP的最小值是( )
A.1.2 B.1.5 C.2.4 D.2.5
8.如图,将长方形ABCD沿对角线BD折叠,使点C落在点C′处,BC′交AD于E,AD=8,AB=4,则重叠部分(即)的面积为( )
A.6 B.7.5 C.10 D.20
9.如图,在中,,点D在AC边上且,M是BD的中点.若,,则CM等于( )
A.5 B.6 C.8 D.10
10.如图,将矩形ABCD折叠,使点C和点A重合,折痕为EF.若,,则EF的长为( )
A. B. C. D.
二、填空题
11.如图,在矩形中,点在上,且平分.若,,则的长为_________.
12.已知,在△ABC中,∠BAC=45°,AB=1,AC=,以AC为一边作等腰直角△ACD,使∠CAD=90°,连接BD,则线段BD的长度为________.
13.如图,在矩形纸片中,点是边的中点,沿直线折叠,点落在矩形内部的点处,连接并延长交于点.已知,,则的长为__________.
14.如图,在中,,,,将绕点旋转,得到,点的对应点为,为的中点,连接.在旋转的过程中,线段长度的最大值为__________.
15.如图,在平行四边形中,,F是的中点,,垂足E在线段上.下列结论①;②;③;④中,一定成立的是_________.(请填序号)
16.如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,E、F分别为DB、BC的中点,若AB=8,则EF=_____.
三、解答题
17.在Rt△ABC中,∠ACB=90°,点D是AB的中点,点E是直线BC上一点(不与点B,C重合),连接CD,DE.
(1)如图1.
①若∠CDE=90°,求证:∠A=∠E.
②若BD平分∠CDE,且∠E=24°,求∠A的度数.
(2)设∠A=α(α>45°),∠DEC=β,若CD=CE,求β关于α的函数关系式,并说明理由.
18.如图,四边形中,,,点是的中点,连接,将沿折叠后得到,且点在四边形内部,延长交于点,连接.
(1)求证:;
(2)求证:;
(3)若点是的中点,,求的长.
19.已知:如图,在四边形中,点在边的延长线上,平分、平分,交于点.
(1)求证:;
(2)若点为的中点,求证:四边形是矩形.
20.如图,在平行四边形中,对角线与相交于点,是等边三角形,,求的面积.
参考答案
1.B
2.B
3.D
4.B
5.B
6.C
7.A
8.C
9.A
10.C
11.
12.或
13.
14.
15.②③④
16.2
17.(1)①见解析;②22°;(2) 或
【详解】
解:(1)①∵D是AB的中点,
∴DA=DC,DB=DC,
∴∠A=∠ACD,∠DCB=∠DBC,
∠ACD+∠DCE=90°
又 ∠EDC=90°,
∠E+∠DCE=90°,
∴∠E=∠ACD,
∠A=∠E.
②由BD平分∠CDE,设∠EDB=∠CDB=x,则∠DCB=∠DBC=24°+x,
在△DBC中,24°+x+24°+x+x=180°,
解得,x=44°,
∵∠A=∠ACD,
∴∠A=22°;
(2)∵CD=CE,
∴∠CDE=∠DEC,
情况1:如图1所示,当点E在线段BC上时,
图1
∠A=∠ACD=α,∠CDE=∠DEC=β,则∠DCE=90°-α
在△DEC中,2β+90°-α=180°,所以.
情况2:如图2所示,当点E在BC延长线上时,
图2
∠A=∠ACD=α,∠CDE=∠DEC=β,则∠DCB=90°-α=2β
所以.
综上所述: 或.
18.(1)见解析;(2)见解析;(3)
【详解】
解:(1)∵E是AD中点,
∴AE=DE,
由折叠可知:AE=EG,∠EGB=∠EGF=∠D=∠A=90°,
∴EG=ED,又EF=EF,
∴Rt△EGF≌Rt△EOF(HL);
(2)△ABE折叠得到△GBE,
∴AB=BG,
∵AD∥BC,∠A=∠D=90°,
∴∠ABC=90°,∠C=90°,
∴四边形ABCD为矩形,
∴AB=DC,
∴BG=CD;
(3)∵点E是AD中点,AD=BC=8,
∴AE=DE=4,
∵点F是CD中点,
∴设CD=x,则DF=x,
则BE2=BG2+EG2,即BE2=CD2+AE2,
即BE2=x2+42,
且EF2=DE2+DF2,即EF2=42+(x)2,
且BF2=BC2+CF2,即BF2=82+(x)2,
∵∠AEB=∠GEB,∠DEF=∠GEF,
∴∠BEF=∠GEB+∠GEF=90°,
∴BF2=BE2+EF2,
∴82+(x)2= x2+42+42+(x)2,
解得:x=,即CD=.
19.(1)见解析;(2)见解析
【详解】
证明:(1)∵平分、平分
∴,
∵∥,
∴,
∴,
∴,,
∴.
(2)∵点为的中点,
∴,又,
∴四边形是平行四边形
∵平分、平分,
∴,
∴
∵,
∴
∵四边形是平行四边形,
∴平行四边形是矩形.
20.
【详解】
解:因为平行四边形,∴,,
又∵三角形是等边三角形
,
∴,
∴
∴平行四边形是矩形
∴°
在中,
由勾股定理得
∴
∴S?ABCD=AB?BC=4×4=16
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在长方形ABCD中,AE平分∠BAD交BC于点E,连接ED,若ED=5,EC=3,则长方形的周长为( )
A.20 B.22 C.24 D.26
2.如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于点G,CDAE.若BD6,CD5,则△DCG的面积是( )
A.10 B.5 C. D.
3.如图,在矩形中,点,分别在边,上,且,将矩形沿直线折叠,使点恰好落在边上的点处,则的长为( )
A.9 B.8 C. D.
4.如图,把长方形纸片沿对角线折叠,设重叠部分为.下列说法错误的是( )
A. B. C. D.△ABE≌△CDE
5.如图,在中,,,,是的中点,则中最短边的长为( )
A. B. C. D.
6.如图,点为矩形的边上的点,于点,且,下列结论不正确的是( )
A.平分 B.为等腰三角形
C. D.
7.如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则CP的最小值是( )
A.1.2 B.1.5 C.2.4 D.2.5
8.如图,将长方形ABCD沿对角线BD折叠,使点C落在点C′处,BC′交AD于E,AD=8,AB=4,则重叠部分(即)的面积为( )
A.6 B.7.5 C.10 D.20
9.如图,在中,,点D在AC边上且,M是BD的中点.若,,则CM等于( )
A.5 B.6 C.8 D.10
10.如图,将矩形ABCD折叠,使点C和点A重合,折痕为EF.若,,则EF的长为( )
A. B. C. D.
二、填空题
11.如图,在矩形中,点在上,且平分.若,,则的长为_________.
12.已知,在△ABC中,∠BAC=45°,AB=1,AC=,以AC为一边作等腰直角△ACD,使∠CAD=90°,连接BD,则线段BD的长度为________.
13.如图,在矩形纸片中,点是边的中点,沿直线折叠,点落在矩形内部的点处,连接并延长交于点.已知,,则的长为__________.
14.如图,在中,,,,将绕点旋转,得到,点的对应点为,为的中点,连接.在旋转的过程中,线段长度的最大值为__________.
15.如图,在平行四边形中,,F是的中点,,垂足E在线段上.下列结论①;②;③;④中,一定成立的是_________.(请填序号)
16.如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,E、F分别为DB、BC的中点,若AB=8,则EF=_____.
三、解答题
17.在Rt△ABC中,∠ACB=90°,点D是AB的中点,点E是直线BC上一点(不与点B,C重合),连接CD,DE.
(1)如图1.
①若∠CDE=90°,求证:∠A=∠E.
②若BD平分∠CDE,且∠E=24°,求∠A的度数.
(2)设∠A=α(α>45°),∠DEC=β,若CD=CE,求β关于α的函数关系式,并说明理由.
18.如图,四边形中,,,点是的中点,连接,将沿折叠后得到,且点在四边形内部,延长交于点,连接.
(1)求证:;
(2)求证:;
(3)若点是的中点,,求的长.
19.已知:如图,在四边形中,点在边的延长线上,平分、平分,交于点.
(1)求证:;
(2)若点为的中点,求证:四边形是矩形.
20.如图,在平行四边形中,对角线与相交于点,是等边三角形,,求的面积.
参考答案
1.B
2.B
3.D
4.B
5.B
6.C
7.A
8.C
9.A
10.C
11.
12.或
13.
14.
15.②③④
16.2
17.(1)①见解析;②22°;(2) 或
【详解】
解:(1)①∵D是AB的中点,
∴DA=DC,DB=DC,
∴∠A=∠ACD,∠DCB=∠DBC,
∠ACD+∠DCE=90°
又 ∠EDC=90°,
∠E+∠DCE=90°,
∴∠E=∠ACD,
∠A=∠E.
②由BD平分∠CDE,设∠EDB=∠CDB=x,则∠DCB=∠DBC=24°+x,
在△DBC中,24°+x+24°+x+x=180°,
解得,x=44°,
∵∠A=∠ACD,
∴∠A=22°;
(2)∵CD=CE,
∴∠CDE=∠DEC,
情况1:如图1所示,当点E在线段BC上时,
图1
∠A=∠ACD=α,∠CDE=∠DEC=β,则∠DCE=90°-α
在△DEC中,2β+90°-α=180°,所以.
情况2:如图2所示,当点E在BC延长线上时,
图2
∠A=∠ACD=α,∠CDE=∠DEC=β,则∠DCB=90°-α=2β
所以.
综上所述: 或.
18.(1)见解析;(2)见解析;(3)
【详解】
解:(1)∵E是AD中点,
∴AE=DE,
由折叠可知:AE=EG,∠EGB=∠EGF=∠D=∠A=90°,
∴EG=ED,又EF=EF,
∴Rt△EGF≌Rt△EOF(HL);
(2)△ABE折叠得到△GBE,
∴AB=BG,
∵AD∥BC,∠A=∠D=90°,
∴∠ABC=90°,∠C=90°,
∴四边形ABCD为矩形,
∴AB=DC,
∴BG=CD;
(3)∵点E是AD中点,AD=BC=8,
∴AE=DE=4,
∵点F是CD中点,
∴设CD=x,则DF=x,
则BE2=BG2+EG2,即BE2=CD2+AE2,
即BE2=x2+42,
且EF2=DE2+DF2,即EF2=42+(x)2,
且BF2=BC2+CF2,即BF2=82+(x)2,
∵∠AEB=∠GEB,∠DEF=∠GEF,
∴∠BEF=∠GEB+∠GEF=90°,
∴BF2=BE2+EF2,
∴82+(x)2= x2+42+42+(x)2,
解得:x=,即CD=.
19.(1)见解析;(2)见解析
【详解】
证明:(1)∵平分、平分
∴,
∵∥,
∴,
∴,
∴,,
∴.
(2)∵点为的中点,
∴,又,
∴四边形是平行四边形
∵平分、平分,
∴,
∴
∵,
∴
∵四边形是平行四边形,
∴平行四边形是矩形.
20.
【详解】
解:因为平行四边形,∴,,
又∵三角形是等边三角形
,
∴,
∴
∴平行四边形是矩形
∴°
在中,
由勾股定理得
∴
∴S?ABCD=AB?BC=4×4=16
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
