2020-2021学年八年级数学北师大版下册 第一章 三角形的证明单元训练卷(Word版 含答案)
文档属性
| 名称 | 2020-2021学年八年级数学北师大版下册 第一章 三角形的证明单元训练卷(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 214.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 17:34:29 | ||
图片预览


文档简介
第一章三角形的证明单元训练卷
一、选择题(共10小题,3*10=30)
1.下列条件中不能判断△ABC为直角三角形的是( )
A.AB2+AC2=BC2
B.∠B∶∠C∶∠A=1∶2∶3
C.∠B+∠C=∠A
D.AB∶BC∶CA=1∶2∶3
2.已知一个等腰三角形的两内角的度数之比为1∶4,则这个等腰三角形顶角的度数为( )
A.20° B.120°
C.20°或120° D.36°
3.如图,在△AEF中,尺规作图如下:分别以点E,点F为圆心,大于EF的长为半径作弧,两弧相交于G,H两点,作直线GH,交EF于点O,连接AO,则下列结论正确的是( )
A.AO平分∠EAF
B.AO垂直平分EF
C.GH垂直平分EF
D.GH平分AF
4.如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点D,DE垂直平分AB,垂足为E,若BC=3,则AD的长为( )
A. B.2 C.2 D.4
5.如图,在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB,垂足为D,则BD?AD的值为( )
A. B.
C. D.
6. 如图,在△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为( )
A.5 B.6 C.8 D.10
7.等边三角形的边长为2,则该三角形的面积为( )
A.4 B.2
C. D.3
8.某市在旧城改造中,计划在一块如图所示的△ABC空地上种植一草皮以美化环境,已知∠A=150°,这种草皮每平方米售价a元,则购买这种草皮至少需要( )
A.300a元 B.150a元
C.450a元 D.225a元
9.等腰三角形一腰上的高与另一腰的夹角为20°,则顶角的度数是( )
A.70° B.110°
C.70°或110° D.20°或160°
10.如图,已知∠MON=30°,点A1,A2,A3……在射线ON上,点B1,B2,B3……在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4……均为等边三角形,若OA1=1,则△A6B6A7的边长为( )
A.6 B.12 C.32 D.64
二.填空题(共8小题,3*8=24)
11. 命题:“如果m是整数,那么它是有理数”,则它的逆命题为:_________________________________.
12. 如图,已知AB⊥CD,垂足为B,BC=BE,若直接应用“HL”判定△ABC≌△DBE,则需要添加的一个条件是_____________.
,
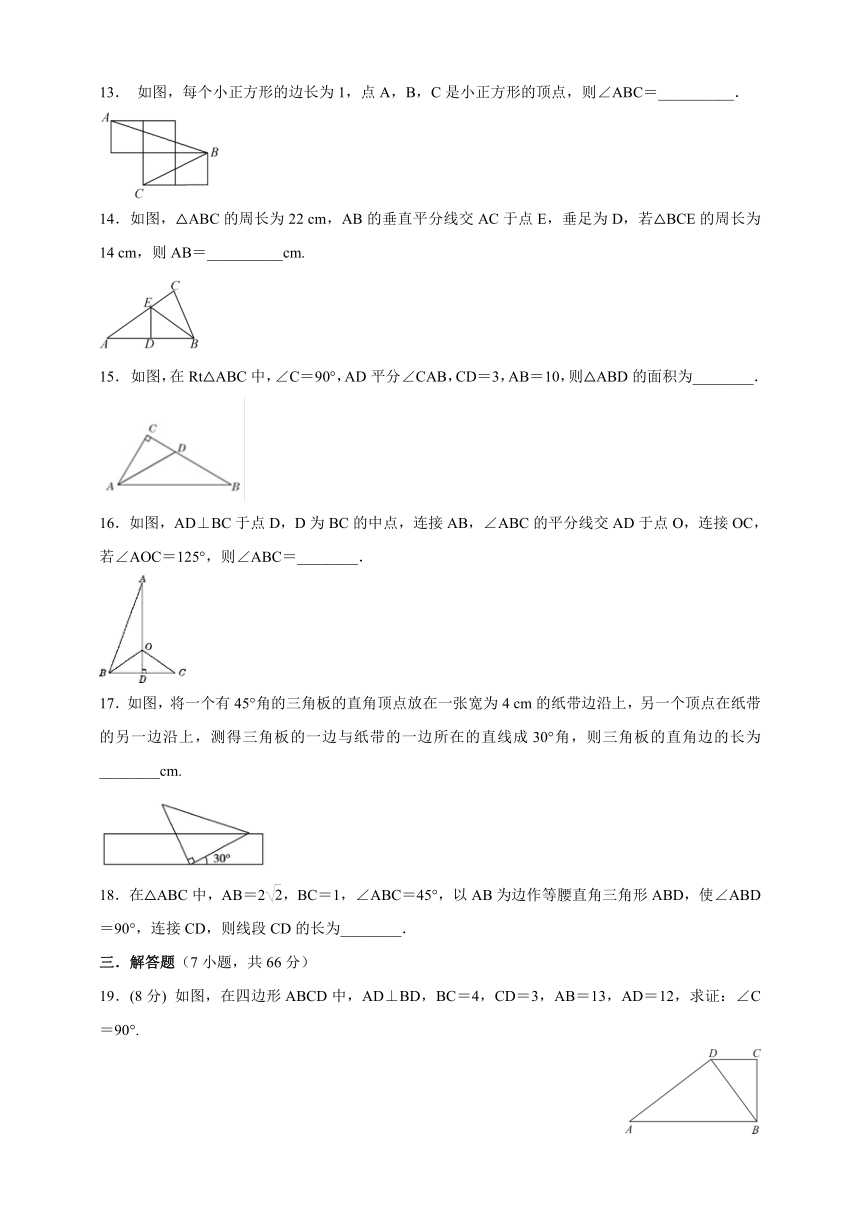
13. 如图,每个小正方形的边长为1,点A,B,C是小正方形的顶点,则∠ABC=__________.
14.如图,△ABC的周长为22 cm,AB的垂直平分线交AC于点E,垂足为D,若△BCE的周长为14 cm,则AB=__________cm.
15. 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,CD=3,AB=10,则△ABD的面积为________.
16.如图,AD⊥BC于点D,D为BC的中点,连接AB,∠ABC的平分线交AD于点O,连接OC,若∠AOC=125°,则∠ABC=________.
17.如图,将一个有45°角的三角板的直角顶点放在一张宽为4 cm的纸带边沿上,另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,则三角板的直角边的长为________cm.
18.在△ABC中,AB=2,BC=1,∠ABC=45°,以AB为边作等腰直角三角形ABD,使∠ABD=90°,连接CD,则线段CD的长为________.
三.解答题(7小题,共66分)
19.(8分) 如图,在四边形ABCD中,AD⊥BD,BC=4,CD=3,AB=13,AD=12,求证:∠C=90°.
20.(8分) 如图,在△ABC中,D为BC的中点,DE⊥BC于点D,交∠BAC的角平分线AE于点E,EF⊥AB于点F,EG⊥AC交AC的延长线于点G,求证:BF=CG.
21.(8分) 如图,在△ABC中,AC=8,∠A=30°,∠B=45°,求AB和BC的长.
22.(10分) 如图,把长方形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处.
(1)求证:B′E=BF;
(2)设AE=a,AB=b,BF=c,试猜想a,b,c之间的一种关系,并给予证明.
23.(10分) 如图,已知∠1=∠2,P为BN上的一点,PF⊥BC于点F,PA=PC.
(1)求证:∠PCB+∠BAP=180°;
(2)若BC=12 cm,AB=6 cm,PA=5 cm,求BP的长.
24.(10分) 如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=,求AD的长.
25.(12分) 数学课上,张老师举了下面的例题:
例1 等腰三角形ABC中,∠A=110°,求∠B的度数.(答案:35°)
例2 等腰三角形ABC中,∠A=40°,求∠B的度数.(答案:40°或70°或100°)
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形ABC中,∠A=80°,求∠B的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,∠A的度数不同,得到∠B的度数的个数也可能不同.如果在等腰三角形ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.
参考答案
1-5DCCCC 6-10CCBCC
11. 如果m是有理数,那么它是整数 12. AC=DE 13. 45° 14. 8 15.15 16.70° 17. 8
18. 或
19. 证明:∵AD⊥BD,AB=13,AD=12,∴BD=5.又∵BC=4,CD=3,∴CD2+BC2=BD2,∴∠C=90°
20. 证明:连接BE,CE,∵D为BC的中点,DE⊥BC,∴EB=EC,∵AE平分∠BAC,EF⊥AB,EG⊥AC,∴EF=EG,∴△BEF≌△CEG(HL),∴BF=CG
21. 解:过点C作CD⊥AB于点D,在Rt△ACD中,∠A=30°,AC=8,∴CD=AC=4,∴AD==4. ∵∠B=45°,CD⊥AB,∴∠B=∠BCD=45°,∴CD=BD=4,∴BC===4,AB=AD+BD=4+4.
22. (1)证明:由题意得B′F=BF,∠B′FE=∠BFE.又∵AD∥BC,∴∠B′EF=∠BFE,∴∠B′FE=∠B′EF,∴B′F=B′E,∴B′E=BF (2)a,b,c的关系为a2+b2=c2,连接BE,则BE=B′E,由(1)知B′E=BF=c,∴BE=c,∵AE2+AB2=BE2,又∵AE=a,AB=b,∴a2+b2=c2(若写a+b>c也可以)
23. M解:(1)证明:过点P作PE⊥AB于点E,∵∠1=∠2,PF⊥BC,PE⊥AB,∴PE=PF.在△APE和△CPF中,∴△APE≌△CPF(HL),∴∠PAE=∠PCB.∵∠PAE+∠PAB=180°,∴∠PCB+∠BAP=180°.
(2)∵△APE≌△CPF,∴AE=FC,∵BC=12 cm,AB=6 cm,∴AE=×(12-6)=3 (cm),BE=AB+AE=6+3=9 (cm),在Rt△PAE中,PE==4 (cm),在Rt△PBE中,PB== (cm).
24. 解:(1)证明:∵BE⊥AC,AD⊥BC,∴∠ADC=∠BEC=90°,∠DAC+∠ACD=∠DBF+∠DCA=90°,∴∠DAC=∠DBE,又∵∠BAD=45°,∴∠BAD=∠DBA,∴AD=BD,∴△ADC≌△BDF(ASA),∴BF=AC,又∵AB=BC,BE⊥AC,∴AE=CE,∴AC=2AE,∴BF=2AE.(2)∵△BFD≌△ACD,∴FD=CD=,∴FC==2,又∵AE=CE,FE⊥AC,∴FC=AF,∴AF=2,∴AD=AF+FD=2+.
25.解:(1)若∠A为顶角,则∠B=(180°-80°)÷2=50°;若∠A为底角,∠B为顶,则∠B=180°-2×80°=20°;若∠A为底角,∠B为底角,则∠B=80°. 故∠B为50°或20°或80°.
(2)分两种情况:①当90≤x<180时,∠A只能为顶角,∴∠B的度数只有一个.
②当0<x<90时,若∠A为顶角,则∠B=°;若∠A为底角,∠B为顶角,则∠B=(180-2x)°;若∠A为底角,∠B为底角,则∠B=x°. 当≠180-2x且180-2x≠x且≠x,即x≠60时,∠B有三个不同的度数.
综上所述,当0<x<90且x≠60时,∠B有三个不同的度数.
一、选择题(共10小题,3*10=30)
1.下列条件中不能判断△ABC为直角三角形的是( )
A.AB2+AC2=BC2
B.∠B∶∠C∶∠A=1∶2∶3
C.∠B+∠C=∠A
D.AB∶BC∶CA=1∶2∶3
2.已知一个等腰三角形的两内角的度数之比为1∶4,则这个等腰三角形顶角的度数为( )
A.20° B.120°
C.20°或120° D.36°
3.如图,在△AEF中,尺规作图如下:分别以点E,点F为圆心,大于EF的长为半径作弧,两弧相交于G,H两点,作直线GH,交EF于点O,连接AO,则下列结论正确的是( )
A.AO平分∠EAF
B.AO垂直平分EF
C.GH垂直平分EF
D.GH平分AF
4.如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点D,DE垂直平分AB,垂足为E,若BC=3,则AD的长为( )
A. B.2 C.2 D.4
5.如图,在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB,垂足为D,则BD?AD的值为( )
A. B.
C. D.
6. 如图,在△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为( )
A.5 B.6 C.8 D.10
7.等边三角形的边长为2,则该三角形的面积为( )
A.4 B.2
C. D.3
8.某市在旧城改造中,计划在一块如图所示的△ABC空地上种植一草皮以美化环境,已知∠A=150°,这种草皮每平方米售价a元,则购买这种草皮至少需要( )
A.300a元 B.150a元
C.450a元 D.225a元
9.等腰三角形一腰上的高与另一腰的夹角为20°,则顶角的度数是( )
A.70° B.110°
C.70°或110° D.20°或160°
10.如图,已知∠MON=30°,点A1,A2,A3……在射线ON上,点B1,B2,B3……在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4……均为等边三角形,若OA1=1,则△A6B6A7的边长为( )
A.6 B.12 C.32 D.64
二.填空题(共8小题,3*8=24)
11. 命题:“如果m是整数,那么它是有理数”,则它的逆命题为:_________________________________.
12. 如图,已知AB⊥CD,垂足为B,BC=BE,若直接应用“HL”判定△ABC≌△DBE,则需要添加的一个条件是_____________.
,
13. 如图,每个小正方形的边长为1,点A,B,C是小正方形的顶点,则∠ABC=__________.
14.如图,△ABC的周长为22 cm,AB的垂直平分线交AC于点E,垂足为D,若△BCE的周长为14 cm,则AB=__________cm.
15. 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,CD=3,AB=10,则△ABD的面积为________.
16.如图,AD⊥BC于点D,D为BC的中点,连接AB,∠ABC的平分线交AD于点O,连接OC,若∠AOC=125°,则∠ABC=________.
17.如图,将一个有45°角的三角板的直角顶点放在一张宽为4 cm的纸带边沿上,另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,则三角板的直角边的长为________cm.
18.在△ABC中,AB=2,BC=1,∠ABC=45°,以AB为边作等腰直角三角形ABD,使∠ABD=90°,连接CD,则线段CD的长为________.
三.解答题(7小题,共66分)
19.(8分) 如图,在四边形ABCD中,AD⊥BD,BC=4,CD=3,AB=13,AD=12,求证:∠C=90°.
20.(8分) 如图,在△ABC中,D为BC的中点,DE⊥BC于点D,交∠BAC的角平分线AE于点E,EF⊥AB于点F,EG⊥AC交AC的延长线于点G,求证:BF=CG.
21.(8分) 如图,在△ABC中,AC=8,∠A=30°,∠B=45°,求AB和BC的长.
22.(10分) 如图,把长方形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处.
(1)求证:B′E=BF;
(2)设AE=a,AB=b,BF=c,试猜想a,b,c之间的一种关系,并给予证明.
23.(10分) 如图,已知∠1=∠2,P为BN上的一点,PF⊥BC于点F,PA=PC.
(1)求证:∠PCB+∠BAP=180°;
(2)若BC=12 cm,AB=6 cm,PA=5 cm,求BP的长.
24.(10分) 如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=,求AD的长.
25.(12分) 数学课上,张老师举了下面的例题:
例1 等腰三角形ABC中,∠A=110°,求∠B的度数.(答案:35°)
例2 等腰三角形ABC中,∠A=40°,求∠B的度数.(答案:40°或70°或100°)
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形ABC中,∠A=80°,求∠B的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,∠A的度数不同,得到∠B的度数的个数也可能不同.如果在等腰三角形ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.
参考答案
1-5DCCCC 6-10CCBCC
11. 如果m是有理数,那么它是整数 12. AC=DE 13. 45° 14. 8 15.15 16.70° 17. 8
18. 或
19. 证明:∵AD⊥BD,AB=13,AD=12,∴BD=5.又∵BC=4,CD=3,∴CD2+BC2=BD2,∴∠C=90°
20. 证明:连接BE,CE,∵D为BC的中点,DE⊥BC,∴EB=EC,∵AE平分∠BAC,EF⊥AB,EG⊥AC,∴EF=EG,∴△BEF≌△CEG(HL),∴BF=CG
21. 解:过点C作CD⊥AB于点D,在Rt△ACD中,∠A=30°,AC=8,∴CD=AC=4,∴AD==4. ∵∠B=45°,CD⊥AB,∴∠B=∠BCD=45°,∴CD=BD=4,∴BC===4,AB=AD+BD=4+4.
22. (1)证明:由题意得B′F=BF,∠B′FE=∠BFE.又∵AD∥BC,∴∠B′EF=∠BFE,∴∠B′FE=∠B′EF,∴B′F=B′E,∴B′E=BF (2)a,b,c的关系为a2+b2=c2,连接BE,则BE=B′E,由(1)知B′E=BF=c,∴BE=c,∵AE2+AB2=BE2,又∵AE=a,AB=b,∴a2+b2=c2(若写a+b>c也可以)
23. M解:(1)证明:过点P作PE⊥AB于点E,∵∠1=∠2,PF⊥BC,PE⊥AB,∴PE=PF.在△APE和△CPF中,∴△APE≌△CPF(HL),∴∠PAE=∠PCB.∵∠PAE+∠PAB=180°,∴∠PCB+∠BAP=180°.
(2)∵△APE≌△CPF,∴AE=FC,∵BC=12 cm,AB=6 cm,∴AE=×(12-6)=3 (cm),BE=AB+AE=6+3=9 (cm),在Rt△PAE中,PE==4 (cm),在Rt△PBE中,PB== (cm).
24. 解:(1)证明:∵BE⊥AC,AD⊥BC,∴∠ADC=∠BEC=90°,∠DAC+∠ACD=∠DBF+∠DCA=90°,∴∠DAC=∠DBE,又∵∠BAD=45°,∴∠BAD=∠DBA,∴AD=BD,∴△ADC≌△BDF(ASA),∴BF=AC,又∵AB=BC,BE⊥AC,∴AE=CE,∴AC=2AE,∴BF=2AE.(2)∵△BFD≌△ACD,∴FD=CD=,∴FC==2,又∵AE=CE,FE⊥AC,∴FC=AF,∴AF=2,∴AD=AF+FD=2+.
25.解:(1)若∠A为顶角,则∠B=(180°-80°)÷2=50°;若∠A为底角,∠B为顶,则∠B=180°-2×80°=20°;若∠A为底角,∠B为底角,则∠B=80°. 故∠B为50°或20°或80°.
(2)分两种情况:①当90≤x<180时,∠A只能为顶角,∴∠B的度数只有一个.
②当0<x<90时,若∠A为顶角,则∠B=°;若∠A为底角,∠B为顶角,则∠B=(180-2x)°;若∠A为底角,∠B为底角,则∠B=x°. 当≠180-2x且180-2x≠x且≠x,即x≠60时,∠B有三个不同的度数.
综上所述,当0<x<90且x≠60时,∠B有三个不同的度数.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
