6.2 同底数幂乘法幂的乘方积的乘方复习课件(39张)
文档属性
| 名称 | 6.2 同底数幂乘法幂的乘方积的乘方复习课件(39张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 765.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 19:04:58 | ||
图片预览










文档简介
同底数幂的乘法
幂的乘方
积的乘方
复习
鲁教版 (五四制)六年级下册
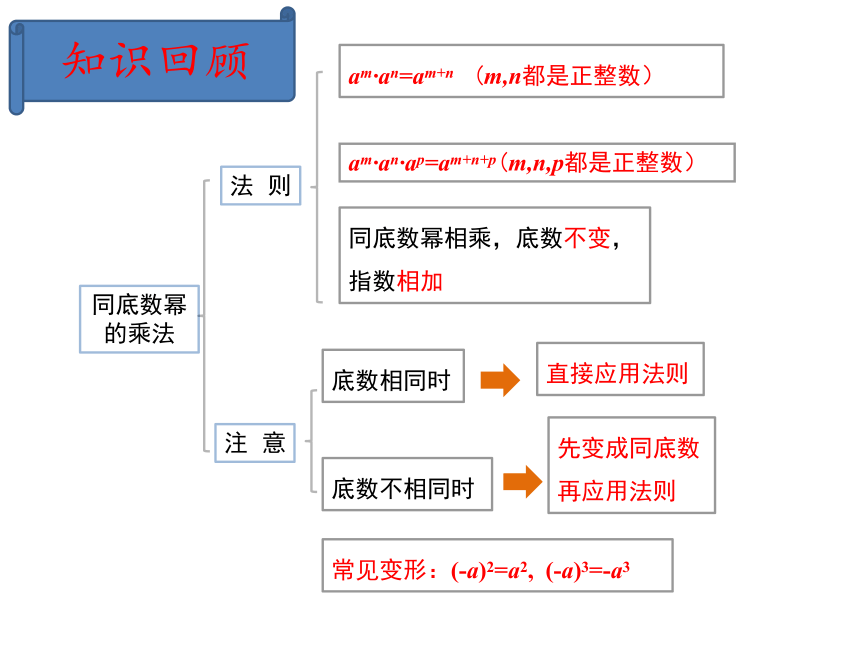
同底数幂的乘法
法则
am·an=am+n (m,n都是正整数)
注意
同底数幂相乘,底数不变,指数相加
am·an·ap=am+n+p(m,n,p都是正整数)
直接应用法则
常见变形:(-a)2=a2, (-a)3=-a3
底数相同时
底数不相同时
先变成同底数再应用法则
知识回顾
?
A .18
B . 12
C . 8
D. 27
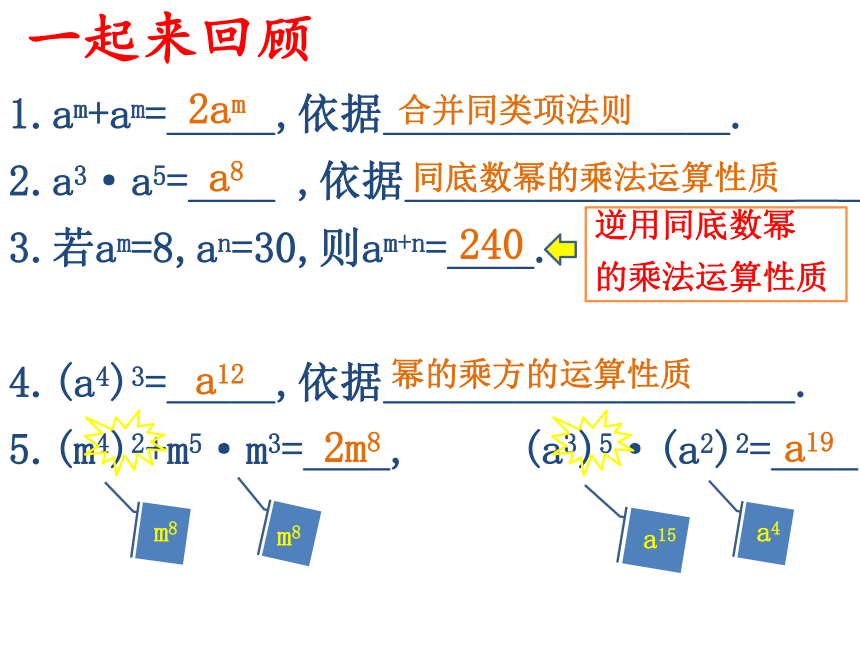
一起来回顾
B
?
?
?
?
?
C
3.下列各式计算正确的是 ( )
?
?
?
?
一起来回顾
D
4. 的运算结果应该是( )
?
?
?
?
C
(2)已知an-3·a2n+1=a10, 求n的值;
解:n-3+2n+1=10,
n=4;
5.(1)已知xa=8, xb=9, 求xa+b的值;
解:xa+b=xa·xb
=8×9=72;
(3) 3×27×9 = 32x-4, 求x的值;
解:3×27×9 =3×33×32=32x-4,
2x-4=6;
x=5.
一起来回顾
(am)n = amn (m,n都是正整数)
底数 ,
幂的乘方,
不变
相乘
幂 的 乘 方的运算 法 则:
指数 .
用语言叙述:
[(am)n]p=
幂的乘方的拓展
(amn)p=amnp
(m,n,p为正整数)
1.am+am=_____,依据________________.
2.a3·a5=____ ,依据__________________ _.
3.若am=8,an=30,则am+n=____.
4.(a4)3=_____,依据___________________.
5.(m4)2+m5·m3=____, (a3)5·(a2)2=____.
2am
合并同类项法则
a8
同底数幂的乘法运算性质
240
a12
幂的乘方的运算性质
2m8
a19
逆用同底数幂
的乘法运算性质
m8
m8
a15
a4
一起来回顾
2.计算:
(1) a5.a3+(2a2)4 (2) (-2a)3-(-a).a2
解:
原式=a8+ 2 4 a 8
=a8+16a8
= 17a8
解:
原式=(-2)3 a3+ a. a2
=-8a3+a3
= -7a3
一起来回顾
【例】计算
1、若am=2,an=3,求① am+n 的值。
② a3m+2n的值。
2、若9×27x = 34x+1,求x的值
解:∵am=2,an=3
∴a 3m+2n=a3m·a2n
=(am)3·(an)2
=23×32
=72
∴ am+n=am·an
=2×3=6
∴ 32 ×33x = 34x+1
即 33x+2 = 34x+1
∴ 3x+2 = 4x+1
x = 1
构建方程
化归思想
解: ∵ 9×27x = 34x+1
逆用公式
一起来回顾
【例1】计算:
⑴ (104)2 ; ⑵ (am)4 (m为正整数); ⑶ - (x3)2;
⑷ (-yn)5 ; ⑸ [(x-y)2]3; ⑹ [(a3)2]5.
⑹ [(a3)2]5 =
=104×2
=108 ;
⑴ (104)2
解:
⑵ (am)4
= am×4
= a4m ;
⑶ -(x3)2
=-x3×2
=-x6 ;
⑷ (-yn)5
=-yn×5
=-y5n ;
⑸ [(x-y)2]3 =
(x-y)2×3
= (x-y)6;
(am)n=amn(m,n都是正整数)
幂的乘方,底数不变,指数相乘
(a3×2)5
=a3×2×5
=a30.
推广:[(am)n]p=(amn)p=amnp
(m、n、p都是正整数).
=-(yn)5
积的乘方= .
(ab)n =
an·bn
积的乘方
乘方的积
(m,n都是正整数)
积中每个因式分别乘方的积
积的乘方法则
你能说出法则中“因式”这两个字的意义吗?
(a+b)n,可以用积的乘方法则计算吗?
即 “(a+b)n= an·bn ” 成立吗?
又 “(a+b)n= an+an ” 成立吗?
(abc)n=an·bn·cn
2.下列运算正确的是( )
A. x.x2=x2 B. (xy)2=xy2 C.(x2)3=x6
C
1.计算 (-x2y)2的结果是( )
A.x4y2 B.-x4y2 C.x2y2 D.-x2y2
A
3. 计算:(1) 82016×0.1252015= ________;
=8
(1) (2m)3 ; (2) (-xy)5; (3) (2×102)2 .
4.计算:
解:
(1)原式= 23 ·m3=8m3;
(2)原式=(-x)5 ·y5=-x5y5;
(3)原式=22 ×(102)2=4 ×104;
D.x2+x2=x4
82015×8×0.1252015
=(8×0.125)2015×8
一起来回顾
(1)(ab2)3=ab6 ( )
×
×
×
(2) (3xy)3=9x3y3 ( )
×
(3) (-2a2)2=-4a4 ( )
(4) (-ab2c)2=a2b4c ( )
判断:
(5) ( )
×
大家来找茬!
5. 用简便方法计算:
一起来回顾
类型一:直接运用幂的运算公式
方法技巧:am·an=am+n(m,n都是正整数),(am)n=amn(m,n都是整数),(ab)n=anbn(n是正整数).
1.计算:
(1)-22(x3)2·(x2)4-(x2)5·(x2)2;
解:-5x14
(2)(-4x3)2-[(-2x)2]3;
解:-48x6
(3)(a-b)(b-a)3·(b-a)4.
解:-(a-b)8
小专题 幂的运算五大类型
类型二:逆用幂的公式运算
2.计算:0.252017×42018-8100×0.5300.
解: 0.252017×42018-8100×0.5300
= 0.252017×42017×4-(23)100×0.5300
= (0.25×4)2017×4-2300×0.5300
= 12017×4-(2×0.5)300
= 4-1300
= 3
3.(1)已知ma=3,mb=5,求m3a+2b的值;
解:∵m3a+2b=(ma)3·(mb)2=33×52=675
(2)已知275=9×3m,求m的值.
解:∵原等式可变为(33)5=32×3m=32+m,即315=3m+2,∴m+2=15,∴m=13
变式训练:(1)计算: ;
(2)已知3×9m×27m=321,求m的值;
解:
(2)因为3×9m×27m
=3×(32)m×(33)m
=3×32m×33m=31+5m,
所以31+5m=321,
所以1+5m=21,
所以m=4.
变式训练:
1.已知x2n=4,求(3x3n)2-4(x2)2n的值;
2.已知xm=8,xn=2,求x2(m+n)的值
1. (3x3n)2-4(x2)2n
=9(x3n)2-4(x2)2n
=9(x2n)3-4(x2n)2
=9×43-4×42
=512.
2. x2(m+n)
=x2m+2n
=x2m×x2n
=(xm)2×(xn)2
=82×22
=64×4
=256.
类型四:比较幂的大小
方法技巧:1.化不同指数的幂为同指数的幂比较大小.2.化不同底数的幂为同底数的幂比较大小.
6.比较216与312的大小.
解:∵216=(24)4=164,
312=(33)4=274,
∵164<274,
∴216<312
7.a=833,b=1625,c=3219,试比较a,b,c的大小.
解:∵a=833=(23)33=299,
b=1625=(24)25=2100,
c=3219=(25)19=295,
∵95<99<100,
∴c<a<b
变式训练:1.比较2333,3222,5111的大小关系。
解:2333=23×111=(23)111=8111
3222=32×111=(32)111=9111
因为:5<8<9
所以:5111<2333<3222
变式训练:2.比较62525,12533,2551的大小关系。
解:因为62525=(54)25=5100,
12533=(53)33=599,
2551=(52)51=5102
而99<100<102,
所以12533<62525<2551
类型五:判断是否整除
方法技巧:利用幂的性质将式子转化为用除数表示.
8.52×32n+1×2n-3n×6n+2(n为整数),能被13整除吗?并说明理由.
解:它能被13整除,
理由:原式=52×(32n×3)×2n-3n×(6n×62)
=75×18n-36×18n
=39×18n=13×3×18n,
∴它能被13整除
讲授新课
你能计算下列两个算式吗?(填空)
(1)
=2( )
=2( )
2
(2)
=a( )
=a( )
(a≠0)
2
2
2
2
2
2
2
2
a
1
3-2
a
a
a
a
am-n
(3) 猜想:
(a≠0, m,n都是正整数,
且m>n)
(4)能不能证明你的结论呢?
5-3
除号相当于分数线
讲授新课
(m-n)个a
m个a
n个a
猜想:
讲授新课
同底数幂相除,底数不变,指数相减。
即
同底数幂的除法法则:
条件:①除法 ②同底数幂
结果:①底数不变 ②指数相减
注意:
(5)讨论为什么a≠0?
讲授新课
补充说明:
(1)底数a可以是单项式、多项式,也可以是分式。 但是a≠0。
(2)同底数幂除法法则的逆用。
am-n=am÷an
典型例题
例1 计算
(1)
(2)
(3)
(4)
解:
(1)
(2)解:
(3)解:
(4)解:
注意事项
注意
最后结果中幂的形式应是最简的.
①幂的指数、底数都应是最简的;
③幂的底数是积的形式时,要再用一次(ab)n=an bn.
②底数中系数不能为负;
若底数不同,先化为同底数,后运用法则。
例题讲解
( 1 ) a6÷a3 = a2
( )
×
a6÷a3 = a3
(2) a5÷a = a5
( )
×
a5÷ a = a4
(-c)4 ÷(-c)2 =c2
( 3 )(-c)4 ÷(-c)2 =-c2
( )
×
例2 判断正错,错误的改正
例3 计算
(1)
(2)
(3)
(1)解:
(2)解:
(3)解:
例题讲解
例4 同底数幂的除法法则逆用
例5 计算
解:原式=
a8 ÷ a6 ×a4
=a8-6+4
=a6
课堂练习
已知:am=3,an=5 求:
am-n的值 (2)a3m-2n的值
解:(1) am-n = am ÷ an = 3÷5 = 0.6
负号不要忘记
1
计算:
把xy看成一个整体
课堂练习
2.计算:
课堂练习
2.下面的计算对不对?如果不对,请改正.
×
×
课堂练习2
(1)
(2)
分析:本例的每个小题,由于底数不同,不能直接运用同底数幂的除法法则计算,但可以先利用其他的幂的运算法则转化为同底数幂的情况,再进行除法运算.
解:(1)
解:(2)
课堂练习3
已知: 10m=3, 10n=2. 求10m-n的值.
1:
解:10m-n=10m÷10n
=3÷2
=1.5
提高创新题
提高创新题
幂的乘方
积的乘方
复习
鲁教版 (五四制)六年级下册
同底数幂的乘法
法则
am·an=am+n (m,n都是正整数)
注意
同底数幂相乘,底数不变,指数相加
am·an·ap=am+n+p(m,n,p都是正整数)
直接应用法则
常见变形:(-a)2=a2, (-a)3=-a3
底数相同时
底数不相同时
先变成同底数再应用法则
知识回顾
?
A .18
B . 12
C . 8
D. 27
一起来回顾
B
?
?
?
?
?
C
3.下列各式计算正确的是 ( )
?
?
?
?
一起来回顾
D
4. 的运算结果应该是( )
?
?
?
?
C
(2)已知an-3·a2n+1=a10, 求n的值;
解:n-3+2n+1=10,
n=4;
5.(1)已知xa=8, xb=9, 求xa+b的值;
解:xa+b=xa·xb
=8×9=72;
(3) 3×27×9 = 32x-4, 求x的值;
解:3×27×9 =3×33×32=32x-4,
2x-4=6;
x=5.
一起来回顾
(am)n = amn (m,n都是正整数)
底数 ,
幂的乘方,
不变
相乘
幂 的 乘 方的运算 法 则:
指数 .
用语言叙述:
[(am)n]p=
幂的乘方的拓展
(amn)p=amnp
(m,n,p为正整数)
1.am+am=_____,依据________________.
2.a3·a5=____ ,依据__________________ _.
3.若am=8,an=30,则am+n=____.
4.(a4)3=_____,依据___________________.
5.(m4)2+m5·m3=____, (a3)5·(a2)2=____.
2am
合并同类项法则
a8
同底数幂的乘法运算性质
240
a12
幂的乘方的运算性质
2m8
a19
逆用同底数幂
的乘法运算性质
m8
m8
a15
a4
一起来回顾
2.计算:
(1) a5.a3+(2a2)4 (2) (-2a)3-(-a).a2
解:
原式=a8+ 2 4 a 8
=a8+16a8
= 17a8
解:
原式=(-2)3 a3+ a. a2
=-8a3+a3
= -7a3
一起来回顾
【例】计算
1、若am=2,an=3,求① am+n 的值。
② a3m+2n的值。
2、若9×27x = 34x+1,求x的值
解:∵am=2,an=3
∴a 3m+2n=a3m·a2n
=(am)3·(an)2
=23×32
=72
∴ am+n=am·an
=2×3=6
∴ 32 ×33x = 34x+1
即 33x+2 = 34x+1
∴ 3x+2 = 4x+1
x = 1
构建方程
化归思想
解: ∵ 9×27x = 34x+1
逆用公式
一起来回顾
【例1】计算:
⑴ (104)2 ; ⑵ (am)4 (m为正整数); ⑶ - (x3)2;
⑷ (-yn)5 ; ⑸ [(x-y)2]3; ⑹ [(a3)2]5.
⑹ [(a3)2]5 =
=104×2
=108 ;
⑴ (104)2
解:
⑵ (am)4
= am×4
= a4m ;
⑶ -(x3)2
=-x3×2
=-x6 ;
⑷ (-yn)5
=-yn×5
=-y5n ;
⑸ [(x-y)2]3 =
(x-y)2×3
= (x-y)6;
(am)n=amn(m,n都是正整数)
幂的乘方,底数不变,指数相乘
(a3×2)5
=a3×2×5
=a30.
推广:[(am)n]p=(amn)p=amnp
(m、n、p都是正整数).
=-(yn)5
积的乘方= .
(ab)n =
an·bn
积的乘方
乘方的积
(m,n都是正整数)
积中每个因式分别乘方的积
积的乘方法则
你能说出法则中“因式”这两个字的意义吗?
(a+b)n,可以用积的乘方法则计算吗?
即 “(a+b)n= an·bn ” 成立吗?
又 “(a+b)n= an+an ” 成立吗?
(abc)n=an·bn·cn
2.下列运算正确的是( )
A. x.x2=x2 B. (xy)2=xy2 C.(x2)3=x6
C
1.计算 (-x2y)2的结果是( )
A.x4y2 B.-x4y2 C.x2y2 D.-x2y2
A
3. 计算:(1) 82016×0.1252015= ________;
=8
(1) (2m)3 ; (2) (-xy)5; (3) (2×102)2 .
4.计算:
解:
(1)原式= 23 ·m3=8m3;
(2)原式=(-x)5 ·y5=-x5y5;
(3)原式=22 ×(102)2=4 ×104;
D.x2+x2=x4
82015×8×0.1252015
=(8×0.125)2015×8
一起来回顾
(1)(ab2)3=ab6 ( )
×
×
×
(2) (3xy)3=9x3y3 ( )
×
(3) (-2a2)2=-4a4 ( )
(4) (-ab2c)2=a2b4c ( )
判断:
(5) ( )
×
大家来找茬!
5. 用简便方法计算:
一起来回顾
类型一:直接运用幂的运算公式
方法技巧:am·an=am+n(m,n都是正整数),(am)n=amn(m,n都是整数),(ab)n=anbn(n是正整数).
1.计算:
(1)-22(x3)2·(x2)4-(x2)5·(x2)2;
解:-5x14
(2)(-4x3)2-[(-2x)2]3;
解:-48x6
(3)(a-b)(b-a)3·(b-a)4.
解:-(a-b)8
小专题 幂的运算五大类型
类型二:逆用幂的公式运算
2.计算:0.252017×42018-8100×0.5300.
解: 0.252017×42018-8100×0.5300
= 0.252017×42017×4-(23)100×0.5300
= (0.25×4)2017×4-2300×0.5300
= 12017×4-(2×0.5)300
= 4-1300
= 3
3.(1)已知ma=3,mb=5,求m3a+2b的值;
解:∵m3a+2b=(ma)3·(mb)2=33×52=675
(2)已知275=9×3m,求m的值.
解:∵原等式可变为(33)5=32×3m=32+m,即315=3m+2,∴m+2=15,∴m=13
变式训练:(1)计算: ;
(2)已知3×9m×27m=321,求m的值;
解:
(2)因为3×9m×27m
=3×(32)m×(33)m
=3×32m×33m=31+5m,
所以31+5m=321,
所以1+5m=21,
所以m=4.
变式训练:
1.已知x2n=4,求(3x3n)2-4(x2)2n的值;
2.已知xm=8,xn=2,求x2(m+n)的值
1. (3x3n)2-4(x2)2n
=9(x3n)2-4(x2)2n
=9(x2n)3-4(x2n)2
=9×43-4×42
=512.
2. x2(m+n)
=x2m+2n
=x2m×x2n
=(xm)2×(xn)2
=82×22
=64×4
=256.
类型四:比较幂的大小
方法技巧:1.化不同指数的幂为同指数的幂比较大小.2.化不同底数的幂为同底数的幂比较大小.
6.比较216与312的大小.
解:∵216=(24)4=164,
312=(33)4=274,
∵164<274,
∴216<312
7.a=833,b=1625,c=3219,试比较a,b,c的大小.
解:∵a=833=(23)33=299,
b=1625=(24)25=2100,
c=3219=(25)19=295,
∵95<99<100,
∴c<a<b
变式训练:1.比较2333,3222,5111的大小关系。
解:2333=23×111=(23)111=8111
3222=32×111=(32)111=9111
因为:5<8<9
所以:5111<2333<3222
变式训练:2.比较62525,12533,2551的大小关系。
解:因为62525=(54)25=5100,
12533=(53)33=599,
2551=(52)51=5102
而99<100<102,
所以12533<62525<2551
类型五:判断是否整除
方法技巧:利用幂的性质将式子转化为用除数表示.
8.52×32n+1×2n-3n×6n+2(n为整数),能被13整除吗?并说明理由.
解:它能被13整除,
理由:原式=52×(32n×3)×2n-3n×(6n×62)
=75×18n-36×18n
=39×18n=13×3×18n,
∴它能被13整除
讲授新课
你能计算下列两个算式吗?(填空)
(1)
=2( )
=2( )
2
(2)
=a( )
=a( )
(a≠0)
2
2
2
2
2
2
2
2
a
1
3-2
a
a
a
a
am-n
(3) 猜想:
(a≠0, m,n都是正整数,
且m>n)
(4)能不能证明你的结论呢?
5-3
除号相当于分数线
讲授新课
(m-n)个a
m个a
n个a
猜想:
讲授新课
同底数幂相除,底数不变,指数相减。
即
同底数幂的除法法则:
条件:①除法 ②同底数幂
结果:①底数不变 ②指数相减
注意:
(5)讨论为什么a≠0?
讲授新课
补充说明:
(1)底数a可以是单项式、多项式,也可以是分式。 但是a≠0。
(2)同底数幂除法法则的逆用。
am-n=am÷an
典型例题
例1 计算
(1)
(2)
(3)
(4)
解:
(1)
(2)解:
(3)解:
(4)解:
注意事项
注意
最后结果中幂的形式应是最简的.
①幂的指数、底数都应是最简的;
③幂的底数是积的形式时,要再用一次(ab)n=an bn.
②底数中系数不能为负;
若底数不同,先化为同底数,后运用法则。
例题讲解
( 1 ) a6÷a3 = a2
( )
×
a6÷a3 = a3
(2) a5÷a = a5
( )
×
a5÷ a = a4
(-c)4 ÷(-c)2 =c2
( 3 )(-c)4 ÷(-c)2 =-c2
( )
×
例2 判断正错,错误的改正
例3 计算
(1)
(2)
(3)
(1)解:
(2)解:
(3)解:
例题讲解
例4 同底数幂的除法法则逆用
例5 计算
解:原式=
a8 ÷ a6 ×a4
=a8-6+4
=a6
课堂练习
已知:am=3,an=5 求:
am-n的值 (2)a3m-2n的值
解:(1) am-n = am ÷ an = 3÷5 = 0.6
负号不要忘记
1
计算:
把xy看成一个整体
课堂练习
2.计算:
课堂练习
2.下面的计算对不对?如果不对,请改正.
×
×
课堂练习2
(1)
(2)
分析:本例的每个小题,由于底数不同,不能直接运用同底数幂的除法法则计算,但可以先利用其他的幂的运算法则转化为同底数幂的情况,再进行除法运算.
解:(1)
解:(2)
课堂练习3
已知: 10m=3, 10n=2. 求10m-n的值.
1:
解:10m-n=10m÷10n
=3÷2
=1.5
提高创新题
提高创新题
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
