_ 2020-2021学年八年级数学北师大版下册第一章《三角形的证明》角平分线解答题专项(一)(Word版 含解析)
文档属性
| 名称 | _ 2020-2021学年八年级数学北师大版下册第一章《三角形的证明》角平分线解答题专项(一)(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 196.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 19:07:07 | ||
图片预览



文档简介
北师大版八年级数学下册第一章《三角形的证明》
角平分线解答题专项(一)
1.如图,△ABC中,∠B>∠A,CD⊥AB于点D,∠ACB的平分线CE交AB于点E.
(1)若∠A=55°,∠B=75°,求∠DCE的度数;
(2)直接写出∠DCE,∠A,∠B之间的等量关系.
2.教材呈现:如图是华师版八年级上册数学教材第96页的部分内容.
定理证明:请根据教材中的分析,结合图①,写出“角平分线的性质定理”完整的证明过程.
定理应用:
如图②,△ABC的周长是12,BO、CO分别平分∠ABC和∠ACB,OD⊥BC于点D,若OD=3,则△ABC的面积为
.
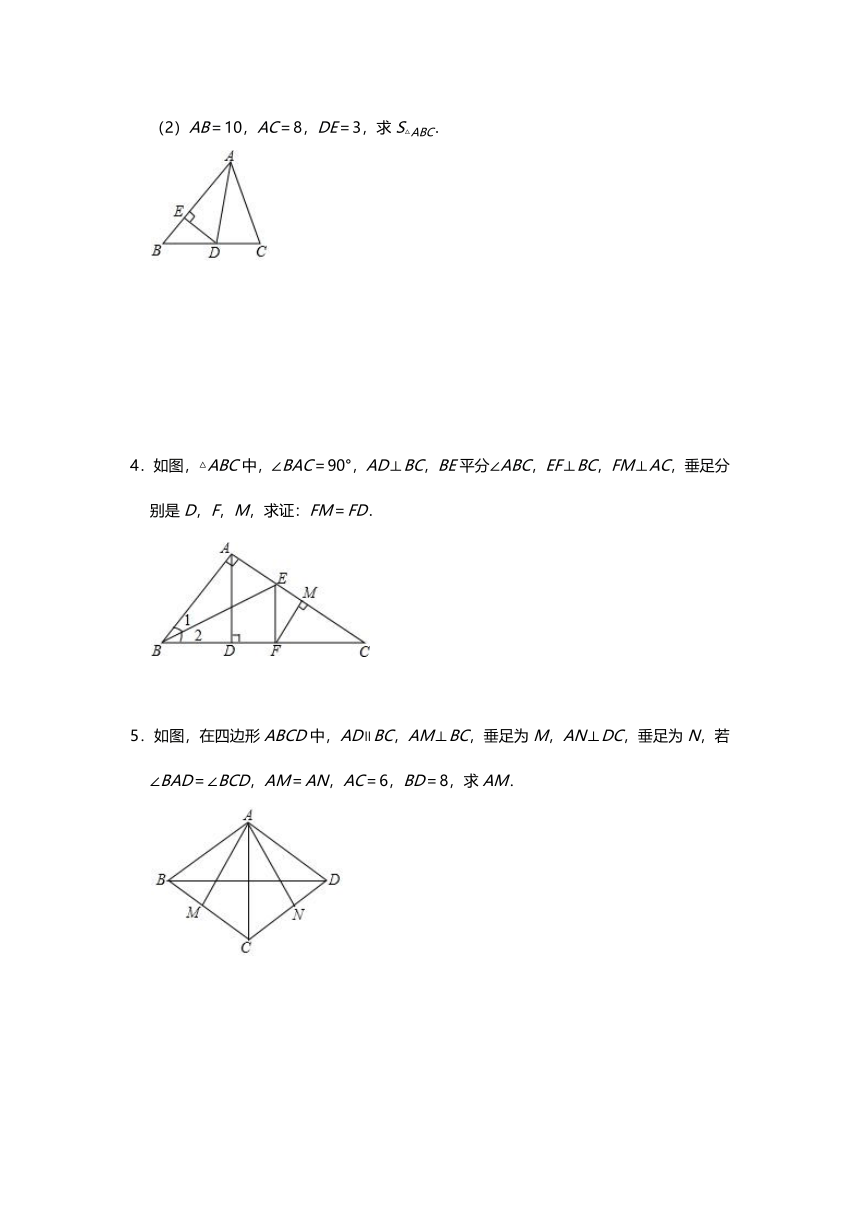
3.已知△ABC中,∠B=50°,∠C=70°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)求∠EDA的度数;
(2)AB=10,AC=8,DE=3,求S△ABC.
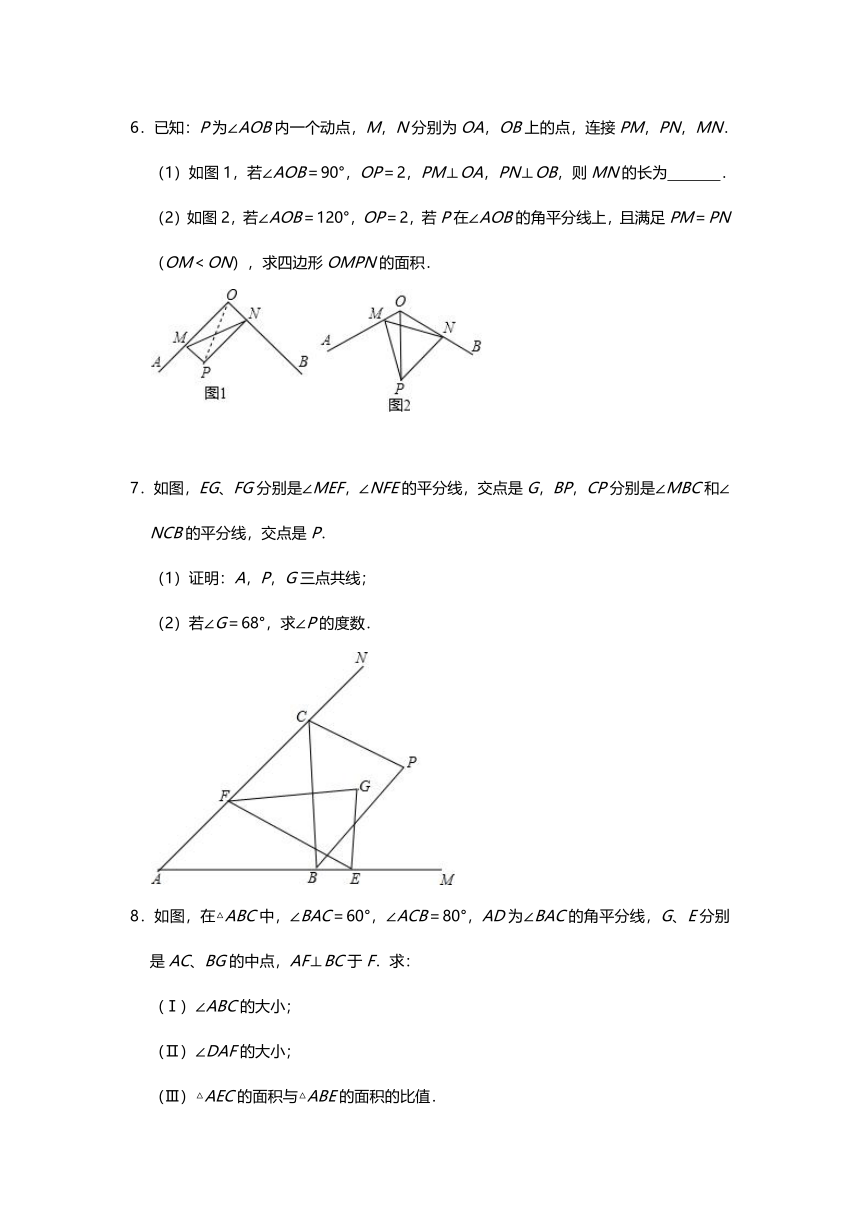
4.如图,△ABC中,∠BAC=90°,AD⊥BC,BE平分∠ABC,EF⊥BC,FM⊥AC,垂足分别是D,F,M,求证:FM=FD.
5.如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N,若∠BAD=∠BCD,AM=AN,AC=6,BD=8,求AM.
6.已知:P为∠AOB内一个动点,M,N分别为OA,OB上的点,连接PM,PN,MN.
(1)如图1,若∠AOB=90°,OP=2,PM⊥OA,PN⊥OB,则MN的长为
.
(2)如图2,若∠AOB=120°,OP=2,若P在∠AOB的角平分线上,且满足PM=PN(OM<ON),求四边形OMPN的面积.
7.如图,EG、FG分别是∠MEF,∠NFE的平分线,交点是G,BP,CP分别是∠MBC和∠NCB的平分线,交点是P.
(1)证明:A,P,G三点共线;
(2)若∠G=68°,求∠P的度数.
8.如图,在△ABC中,∠BAC=60°,∠ACB=80°,AD为∠BAC的角平分线,G、E分别是AC、BG的中点,AF⊥BC于F.求:
(Ⅰ)∠ABC的大小;
(Ⅱ)∠DAF的大小;
(Ⅲ)△AEC的面积与△ABE的面积的比值.
9.如图,D是∠MAN内部一点,点B是射线AM上一点,DE⊥AM于E,DF⊥AN于F,且DE=DF,连接AD.
(1)求证:AD平分∠MAN;(可不用全等)
(2)在射线AN上取一点C,使得DC=DB,若AB=6,BE=2,则AC长为
.
10.已知,如图,BD、CD是△ABC外角的平分线,DE⊥AB,DF⊥AC,求证:点D在∠A平分线上.
11.在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F.
(1)若BE=CF,求证:AD是△ABC的角平分线.
(2)若AD是△ABC的角平分线,求证:BE=CF.
12.已知:如图所示,在△ABC中,AD是△ABC的角平分线,E、F分别是AB,AC上的点,并且有∠EDF+∠EAF=180°,DG⊥AB于点G.
(1)试判断DE和DF的数量关系,并说明理由;
(2)若△ADF和△AED的面积分别为50和39,求△EDG的面积.
13.如图所示,若AB∥CD,AP,CP分别平分∠BAC和∠ACD,PE⊥AC于点E,且PE=3cm,求AB与CD之间的距离.
14.如图,在△ABC中,AC>AB,D是BA延长线上一点,点E是∠CAD平分线上一点,过点E作EM⊥AC于点M,EN⊥AD于点N,BE=CE.
(1)请你在不添加辅助线的情况下写出一对你认为全等的三角形,并加以证明;
(2)若AB=8,AC=10,求AM的长度.
15.如图,Rt△ABC的角平分线AD与BE相交于F,M是DE的中点,设FM=2.5,S△DEF=15,求CD,AB的长.
参考答案
1.解:(1)∵∠A=55°,∠B=75°,
∴∠ACB=50°,
∵CE平分∠ACB,
∴∠BCE=25°,
∵∠B=75°,CD⊥AB,
∴∠BCD=15°,
∴∠DCE=∠ECB﹣∠BCD=25°﹣15°=10°,
即∠DCE的度数是10°;
(2)∠DCE=(∠B﹣∠A),
理由:∵∠ACB=180°﹣∠A﹣∠B,CE平分∠ACB,
∴∠BCE=(180°﹣∠A﹣∠B),
∵CD⊥AB,
∴∠BCD=90°﹣∠B,
∴∠DCE=∠ECB﹣∠BCD=(180°﹣∠A﹣∠B)﹣(90°﹣∠B)=90°﹣∠A﹣∠B﹣90°+∠B=(∠B﹣∠A),
即∠DCE=(∠B﹣∠A).
2.定理证明:∵OC是∠AOB的角平分线,
∴∠AOP=∠BOP,
∵PD⊥OA,PE⊥OB,
∴PE=PD,
在△OEP和△ODP中,
∵,
∴△OEP≌△ODP(AAS),
∴PE=PD;
定理应用:过O作OE⊥AB与E,OF⊥AC于F,
∵BO、CO分别平分∠ABC和∠ACB,
∴EO=DO,OF=DO,
∵OD=3,
∴EO=FO=3,
∵△ABC的周长是12,
∴AB+BC+AC=12,
∴△ABC的面积:AB?EO+AC?FO+CB?DO=(AB+AC+BC)=×12=18,
故答案为:18.
3.解:(1)∵∠B=50°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣50°﹣70°=60°,
∵AD是△ABC的角平分线,
∴∠BAD=∠BAC=×60°=30°,
∵DE⊥AB,
∴∠DEA=90°,
∴∠EDA=180°﹣∠BAD﹣∠DEA=180°﹣30°﹣90°=60°;
(2)如图,过D作DF⊥AC于F,
∵AD是△ABC的角平分线,DE⊥AB,
∴DF=DE=3,
又∵AB=10,AC=8,
∴S△ABC=×AB×DE+×AC×DF=×10×3+×8×3=27.
4.证明:作EH⊥AD于H,
则四边形FDFE是矩形,
∴DF=HE,
∵BE平分∠ABC,EF⊥BC,∠BAC=90°,
∴EA=EF,
∵AD⊥BC,EF⊥BC,
∴AD∥EF,
∴∠HAE=∠MEF,
在△HAE和△MEF中,
,
∴△HAE≌△MEF,
∴EH=MF,
∴FM=FD.
5.
AM=.
6.(1)2;
(2)过P作PG⊥OA,PH⊥OB,
∵P在∠AOB的角平分线上,
∴PG=PH,
在Rt△PGM与Rt△PHN中,,
∴Rt△PGM≌Rt△PHN,
∵∠AOB=120°,
∴∠POA=∠POB=60°,
∴OG=OH=1,PG=PH=,
∴四边形OMPN的面积=四边形PGOH的面积=2△OPG的面积=2××=.
7.解:(1)过G作GP⊥AN于P,GQ⊥AM于Q,PR⊥EF于R,
∵EG、FG分别是∠MEF,∠NFE的平分线,
∴GP=GR=GQ,
∴G在∠NAN的角平分线上,
同理点P在∠NAN的角平分线上,
∴A,P,G三点共线;
(2)∵EQ、FQ分别是∠MEF和∠NFE的平分线,
∴∠QFE=∠NFE,∠QEF=∠MEF,
∴∠Q=180°﹣∠NFE﹣∠MEF
=180°﹣(∠NFE+∠MEF)
=180°﹣(360°﹣∠AFE﹣∠AEF)
=180°﹣(180°+∠A)
=90°﹣∠A=68°,
同理,∠P=90°﹣∠A=68°.
8.解:(Ⅰ)∵在△ABC中,∠BAC=60°,∠ACB=80°,
∴∠ABC=180°﹣60°﹣80°=40°;
(Ⅱ)∵AD为∠BAC的角平分线,
∴∠BAD=∠BAC=30°,
∴∠ADC=∠ABC+∠BAD=70°,
∵AF⊥BC,
∴∠AFD=90°,
∴∠DAF=20°,
(Ⅲ)∵G、E分别是AC、BG的中点,
∴△AEC的面积=S△ABC,△ABE的面积=S△ABC,
∴△AEC的面积与△ABE的面积的比值=2.
9.(1)证明:∵D是∠MAN内部一点,DE⊥AM于E,DF⊥AN于F,且DE=DF,
∴AD平分∠MAN;
(2)解:
分两种情况:
①如图1,当点C在线段AF上时,
∵DE⊥AM于E,DF⊥AN于F,
∴∠DEB=∠DFC=90°,
在Rt△DEB和Rt△DFC中,
,
∴Rt△DEB≌Rt△DFC,
∴CF=BE=2,
∴AC=AB=6,
②如图2,当点C在线段AF的延长线上时,
同理可证Rt△DEB≌Rt△DFC,
∴CF=BE=2,
∵AF=AE=AB+BE=8,
∴AC=8+2=10.
故答案为:6或10.
10.证明:过点D作DG⊥BC,
∵DB是∠CBE的平分线,CD是∠BCF的平分线,DE⊥AB,DF⊥AC,
∴DE=DG,DG=DF,
∴DE=DF,
∴点D在∠A平分线上.
11.证明:(1)∵DE⊥AB,DF⊥AC,
∴△BDE△DCF是直角三角形.
在Rt△BDE与Rt△DCF中,
,
∴Rt△BDE≌Rt△DCF(HL),
∴DE=DF,
又∵DE⊥AB,DF⊥AC,
∴AD是△ABC的角平分线;
(2)∵AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,
∵AD是BC边的中线,
∴BD=CD,
在Rt△BDE和Rt△CDF中,
,
∴Rt△BDE≌Rt△CDF(HL),
∴BE=CF.
12.(1)证明:过D作DN⊥AC于N,∵DG⊥AB于点G,
∴∠EGD=∠FND=90°,
∵AD平分∠BAC,DG⊥AB,DN⊥AC,
∴DG=DN(角平分线性质),
∵∠EAF+∠EDF=180°,
∴∠AED+∠AFD=360°﹣180°=180°,
∵∠AED+∠DEG=180°,
∴∠GED=∠NFD,
在△EGD和△FND中
,
∴△EMD≌△FND(AAS),
∴DE=DF;
(2)解:作DM=DE交AC于M,
∵DE=DF,DM=DE,
∴DM=DF,
∵AD是△ABC的角平分线,DG⊥AB,
∴DG=DN,
在Rt△DEG和Rt△DMN中,
,
∴△DEG≌△DNM(HL),
∵△ADF和△AED的面积分别为50和39,
∴S△MDF=S△ADF﹣S△ADM=50﹣39=11,
S△DNM=S△DEG=S△MDG==5.5.
13.解:如图,过点P作PM⊥AB于M,作PN⊥CD于N,
∵AP、CP分别平分∠BAC和∠ACD,PE⊥AC,
∴PM=PE=PN=3cm,
∴AB与CD之间的距离=PM+PN=3+3=6(cm).
14.解:
(1)△EAN≌△EAM,
证明如下:
∵EA平分∠CAD,
∴∠EAN=∠EAM,
∵EM⊥AC,EN⊥AD,
∴∠ENA=∠EMA=90°,
在△EAN和△EAM中
∴△EAN≌△EAM(AAS);
(2)由(1)可知EN=EM,
在Rt△△ENB和Rt△EMC中,
∴Rt△ENB≌Rt△EMC(HL),
∴AC=NB=10,
∴NA=BN﹣AB=10﹣8=2,
又由(1)可知AM=NA,
∴AM=2.
15.AB=30,CD=8或9.
角平分线解答题专项(一)
1.如图,△ABC中,∠B>∠A,CD⊥AB于点D,∠ACB的平分线CE交AB于点E.
(1)若∠A=55°,∠B=75°,求∠DCE的度数;
(2)直接写出∠DCE,∠A,∠B之间的等量关系.
2.教材呈现:如图是华师版八年级上册数学教材第96页的部分内容.
定理证明:请根据教材中的分析,结合图①,写出“角平分线的性质定理”完整的证明过程.
定理应用:
如图②,△ABC的周长是12,BO、CO分别平分∠ABC和∠ACB,OD⊥BC于点D,若OD=3,则△ABC的面积为
.
3.已知△ABC中,∠B=50°,∠C=70°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)求∠EDA的度数;
(2)AB=10,AC=8,DE=3,求S△ABC.
4.如图,△ABC中,∠BAC=90°,AD⊥BC,BE平分∠ABC,EF⊥BC,FM⊥AC,垂足分别是D,F,M,求证:FM=FD.
5.如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N,若∠BAD=∠BCD,AM=AN,AC=6,BD=8,求AM.
6.已知:P为∠AOB内一个动点,M,N分别为OA,OB上的点,连接PM,PN,MN.
(1)如图1,若∠AOB=90°,OP=2,PM⊥OA,PN⊥OB,则MN的长为
.
(2)如图2,若∠AOB=120°,OP=2,若P在∠AOB的角平分线上,且满足PM=PN(OM<ON),求四边形OMPN的面积.
7.如图,EG、FG分别是∠MEF,∠NFE的平分线,交点是G,BP,CP分别是∠MBC和∠NCB的平分线,交点是P.
(1)证明:A,P,G三点共线;
(2)若∠G=68°,求∠P的度数.
8.如图,在△ABC中,∠BAC=60°,∠ACB=80°,AD为∠BAC的角平分线,G、E分别是AC、BG的中点,AF⊥BC于F.求:
(Ⅰ)∠ABC的大小;
(Ⅱ)∠DAF的大小;
(Ⅲ)△AEC的面积与△ABE的面积的比值.
9.如图,D是∠MAN内部一点,点B是射线AM上一点,DE⊥AM于E,DF⊥AN于F,且DE=DF,连接AD.
(1)求证:AD平分∠MAN;(可不用全等)
(2)在射线AN上取一点C,使得DC=DB,若AB=6,BE=2,则AC长为
.
10.已知,如图,BD、CD是△ABC外角的平分线,DE⊥AB,DF⊥AC,求证:点D在∠A平分线上.
11.在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F.
(1)若BE=CF,求证:AD是△ABC的角平分线.
(2)若AD是△ABC的角平分线,求证:BE=CF.
12.已知:如图所示,在△ABC中,AD是△ABC的角平分线,E、F分别是AB,AC上的点,并且有∠EDF+∠EAF=180°,DG⊥AB于点G.
(1)试判断DE和DF的数量关系,并说明理由;
(2)若△ADF和△AED的面积分别为50和39,求△EDG的面积.
13.如图所示,若AB∥CD,AP,CP分别平分∠BAC和∠ACD,PE⊥AC于点E,且PE=3cm,求AB与CD之间的距离.
14.如图,在△ABC中,AC>AB,D是BA延长线上一点,点E是∠CAD平分线上一点,过点E作EM⊥AC于点M,EN⊥AD于点N,BE=CE.
(1)请你在不添加辅助线的情况下写出一对你认为全等的三角形,并加以证明;
(2)若AB=8,AC=10,求AM的长度.
15.如图,Rt△ABC的角平分线AD与BE相交于F,M是DE的中点,设FM=2.5,S△DEF=15,求CD,AB的长.
参考答案
1.解:(1)∵∠A=55°,∠B=75°,
∴∠ACB=50°,
∵CE平分∠ACB,
∴∠BCE=25°,
∵∠B=75°,CD⊥AB,
∴∠BCD=15°,
∴∠DCE=∠ECB﹣∠BCD=25°﹣15°=10°,
即∠DCE的度数是10°;
(2)∠DCE=(∠B﹣∠A),
理由:∵∠ACB=180°﹣∠A﹣∠B,CE平分∠ACB,
∴∠BCE=(180°﹣∠A﹣∠B),
∵CD⊥AB,
∴∠BCD=90°﹣∠B,
∴∠DCE=∠ECB﹣∠BCD=(180°﹣∠A﹣∠B)﹣(90°﹣∠B)=90°﹣∠A﹣∠B﹣90°+∠B=(∠B﹣∠A),
即∠DCE=(∠B﹣∠A).
2.定理证明:∵OC是∠AOB的角平分线,
∴∠AOP=∠BOP,
∵PD⊥OA,PE⊥OB,
∴PE=PD,
在△OEP和△ODP中,
∵,
∴△OEP≌△ODP(AAS),
∴PE=PD;
定理应用:过O作OE⊥AB与E,OF⊥AC于F,
∵BO、CO分别平分∠ABC和∠ACB,
∴EO=DO,OF=DO,
∵OD=3,
∴EO=FO=3,
∵△ABC的周长是12,
∴AB+BC+AC=12,
∴△ABC的面积:AB?EO+AC?FO+CB?DO=(AB+AC+BC)=×12=18,
故答案为:18.
3.解:(1)∵∠B=50°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣50°﹣70°=60°,
∵AD是△ABC的角平分线,
∴∠BAD=∠BAC=×60°=30°,
∵DE⊥AB,
∴∠DEA=90°,
∴∠EDA=180°﹣∠BAD﹣∠DEA=180°﹣30°﹣90°=60°;
(2)如图,过D作DF⊥AC于F,
∵AD是△ABC的角平分线,DE⊥AB,
∴DF=DE=3,
又∵AB=10,AC=8,
∴S△ABC=×AB×DE+×AC×DF=×10×3+×8×3=27.
4.证明:作EH⊥AD于H,
则四边形FDFE是矩形,
∴DF=HE,
∵BE平分∠ABC,EF⊥BC,∠BAC=90°,
∴EA=EF,
∵AD⊥BC,EF⊥BC,
∴AD∥EF,
∴∠HAE=∠MEF,
在△HAE和△MEF中,
,
∴△HAE≌△MEF,
∴EH=MF,
∴FM=FD.
5.
AM=.
6.(1)2;
(2)过P作PG⊥OA,PH⊥OB,
∵P在∠AOB的角平分线上,
∴PG=PH,
在Rt△PGM与Rt△PHN中,,
∴Rt△PGM≌Rt△PHN,
∵∠AOB=120°,
∴∠POA=∠POB=60°,
∴OG=OH=1,PG=PH=,
∴四边形OMPN的面积=四边形PGOH的面积=2△OPG的面积=2××=.
7.解:(1)过G作GP⊥AN于P,GQ⊥AM于Q,PR⊥EF于R,
∵EG、FG分别是∠MEF,∠NFE的平分线,
∴GP=GR=GQ,
∴G在∠NAN的角平分线上,
同理点P在∠NAN的角平分线上,
∴A,P,G三点共线;
(2)∵EQ、FQ分别是∠MEF和∠NFE的平分线,
∴∠QFE=∠NFE,∠QEF=∠MEF,
∴∠Q=180°﹣∠NFE﹣∠MEF
=180°﹣(∠NFE+∠MEF)
=180°﹣(360°﹣∠AFE﹣∠AEF)
=180°﹣(180°+∠A)
=90°﹣∠A=68°,
同理,∠P=90°﹣∠A=68°.
8.解:(Ⅰ)∵在△ABC中,∠BAC=60°,∠ACB=80°,
∴∠ABC=180°﹣60°﹣80°=40°;
(Ⅱ)∵AD为∠BAC的角平分线,
∴∠BAD=∠BAC=30°,
∴∠ADC=∠ABC+∠BAD=70°,
∵AF⊥BC,
∴∠AFD=90°,
∴∠DAF=20°,
(Ⅲ)∵G、E分别是AC、BG的中点,
∴△AEC的面积=S△ABC,△ABE的面积=S△ABC,
∴△AEC的面积与△ABE的面积的比值=2.
9.(1)证明:∵D是∠MAN内部一点,DE⊥AM于E,DF⊥AN于F,且DE=DF,
∴AD平分∠MAN;
(2)解:
分两种情况:
①如图1,当点C在线段AF上时,
∵DE⊥AM于E,DF⊥AN于F,
∴∠DEB=∠DFC=90°,
在Rt△DEB和Rt△DFC中,
,
∴Rt△DEB≌Rt△DFC,
∴CF=BE=2,
∴AC=AB=6,
②如图2,当点C在线段AF的延长线上时,
同理可证Rt△DEB≌Rt△DFC,
∴CF=BE=2,
∵AF=AE=AB+BE=8,
∴AC=8+2=10.
故答案为:6或10.
10.证明:过点D作DG⊥BC,
∵DB是∠CBE的平分线,CD是∠BCF的平分线,DE⊥AB,DF⊥AC,
∴DE=DG,DG=DF,
∴DE=DF,
∴点D在∠A平分线上.
11.证明:(1)∵DE⊥AB,DF⊥AC,
∴△BDE△DCF是直角三角形.
在Rt△BDE与Rt△DCF中,
,
∴Rt△BDE≌Rt△DCF(HL),
∴DE=DF,
又∵DE⊥AB,DF⊥AC,
∴AD是△ABC的角平分线;
(2)∵AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,
∵AD是BC边的中线,
∴BD=CD,
在Rt△BDE和Rt△CDF中,
,
∴Rt△BDE≌Rt△CDF(HL),
∴BE=CF.
12.(1)证明:过D作DN⊥AC于N,∵DG⊥AB于点G,
∴∠EGD=∠FND=90°,
∵AD平分∠BAC,DG⊥AB,DN⊥AC,
∴DG=DN(角平分线性质),
∵∠EAF+∠EDF=180°,
∴∠AED+∠AFD=360°﹣180°=180°,
∵∠AED+∠DEG=180°,
∴∠GED=∠NFD,
在△EGD和△FND中
,
∴△EMD≌△FND(AAS),
∴DE=DF;
(2)解:作DM=DE交AC于M,
∵DE=DF,DM=DE,
∴DM=DF,
∵AD是△ABC的角平分线,DG⊥AB,
∴DG=DN,
在Rt△DEG和Rt△DMN中,
,
∴△DEG≌△DNM(HL),
∵△ADF和△AED的面积分别为50和39,
∴S△MDF=S△ADF﹣S△ADM=50﹣39=11,
S△DNM=S△DEG=S△MDG==5.5.
13.解:如图,过点P作PM⊥AB于M,作PN⊥CD于N,
∵AP、CP分别平分∠BAC和∠ACD,PE⊥AC,
∴PM=PE=PN=3cm,
∴AB与CD之间的距离=PM+PN=3+3=6(cm).
14.解:
(1)△EAN≌△EAM,
证明如下:
∵EA平分∠CAD,
∴∠EAN=∠EAM,
∵EM⊥AC,EN⊥AD,
∴∠ENA=∠EMA=90°,
在△EAN和△EAM中
∴△EAN≌△EAM(AAS);
(2)由(1)可知EN=EM,
在Rt△△ENB和Rt△EMC中,
∴Rt△ENB≌Rt△EMC(HL),
∴AC=NB=10,
∴NA=BN﹣AB=10﹣8=2,
又由(1)可知AM=NA,
∴AM=2.
15.AB=30,CD=8或9.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
