28.2 解直角三角形及其应用同步练习(Word版 含答案)
文档属性
| 名称 | 28.2 解直角三角形及其应用同步练习(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 180.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 19:11:38 | ||
图片预览


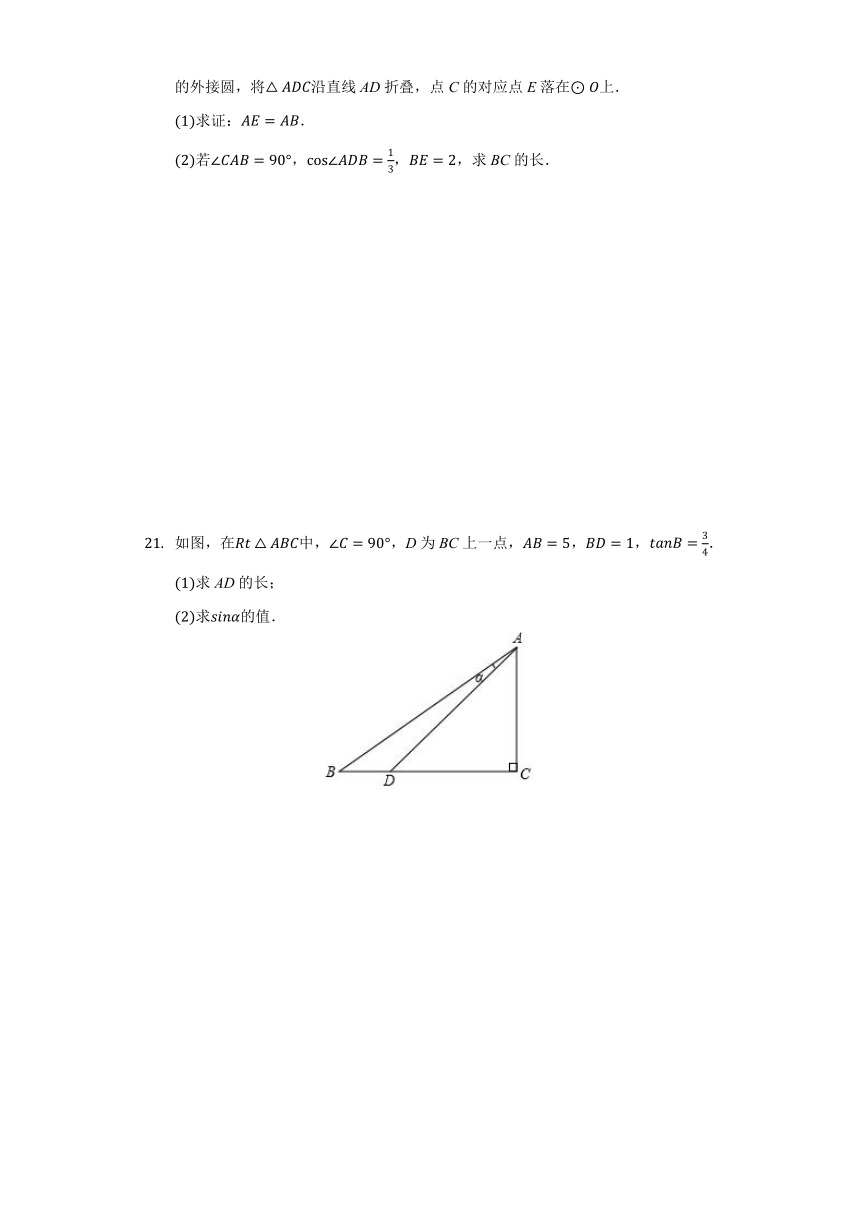
文档简介
解直角三角形及其应用练习
一、选择题
在中,,,,则的度数为???
A.
B.
C.
D.
如果一个等腰三角形的底角为,腰长为,那么这个三角形的面积为
A.
B.
C.
D.
如图,从地面B处测得热气球A的仰角为,从地面C处测得热气球A的仰角为若BC为,则热气球A的高度为?
???
A.
B.
C.
D.
如图,一艘海轮位于灯塔P的南偏东方向,距离灯塔40?海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的正东方向上的B处.这时,B处与灯塔P的距离BP的长可以表示为
A.
40海里
B.
海里
C.
海里
D.
海里
已知圆锥的底面半径为5cm,侧面积为,设圆锥的母线与高的夹角为,则的值为
A.
B.
C.
D.
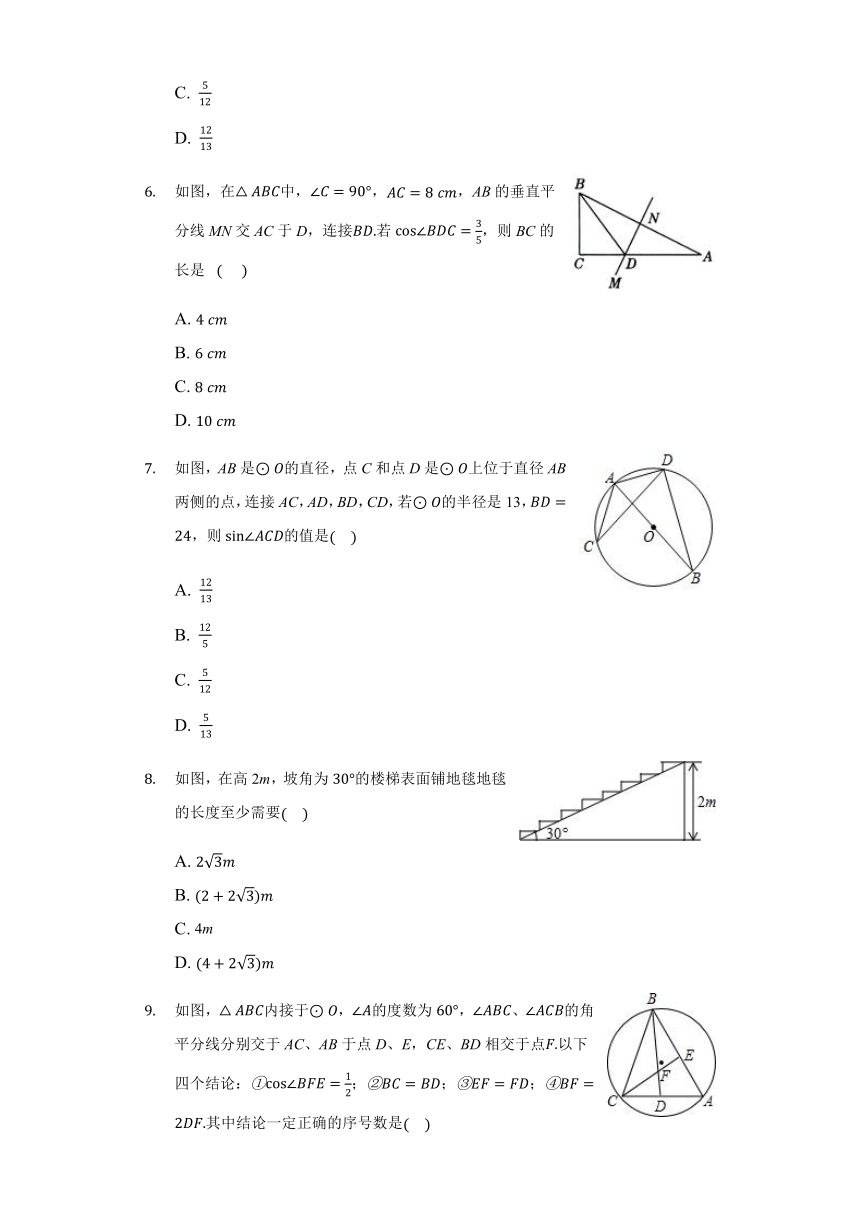
如图,在中,,,AB的垂直平分线MN交AC于D,连接若,则BC的长是?
???
A.
B.
C.
D.
如图,AB是的直径,点C和点D是上位于直径AB两侧的点,连接AC,AD,BD,CD,若的半径是13,,则的值是
A.
B.
C.
D.
如图,在高2m,坡角为的楼梯表面铺地毯地毯的长度至少需要
A.
B.
C.
4m
D.
如图,内接于,的度数为,、的角平分线分别交于AC、AB于点D、E,CE、BD相交于点以下四个结论:;;;其中结论一定正确的序号数是
A.
B.
C.
D.
在中,,,,则直角边BC的长是
A.
B.
C.
D.
如图,以坐标原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是上一点不与A,B重合,连接OP,设,则点P的坐标是
A.
B.
C.
D.
如图,中,,,,以点B为圆心,r为半径作,当时,与AC的位置关系是
A.
相离
B.
相切
C.
相交
D.
无法确定
如图,在山坡上种树,坡度:2,,则相邻两树的水平距离AC为
A.
5m
B.
C.
D.
10m
二、填空题
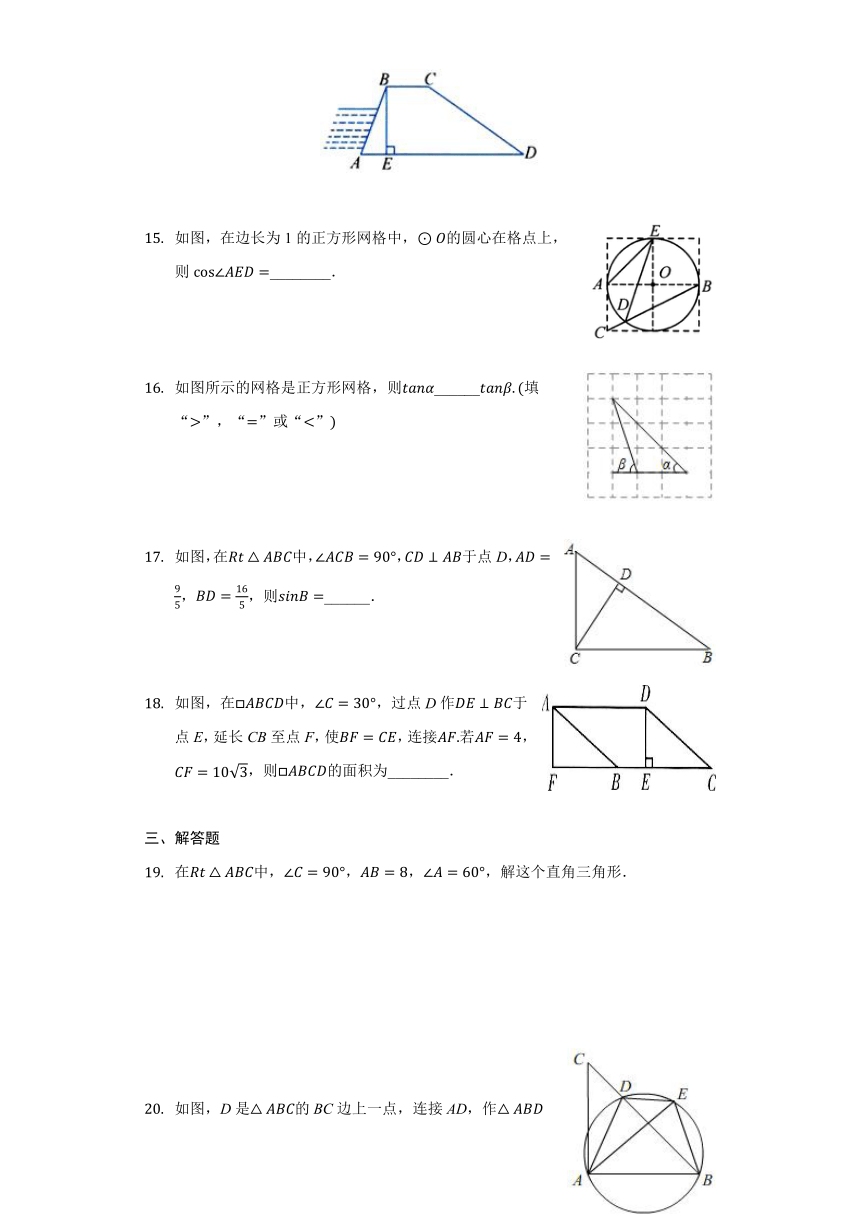
如图,某河堤的横断面是梯形ABCD,,于点E,米,米,,求AD的长度.
如图,在边长为1的正方形网格中,的圆心在格点上,则________.
如图所示的网格是正方形网格,则______填“”,“”或“”
如图,在中,,于点D,,,则______.
如图,在中,,过点D作于点E,延长CB至点F,使,连接若,,则的面积为________.
三、解答题
在中,,,,解这个直角三角形.
如图,D是的BC边上一点,连接AD,作的外接圆,将沿直线AD折叠,点C的对应点E落在上.
求证:.
若,,,求BC的长.
如图,在中,,D为BC上一点,,,.
求AD的长;
求的值.
如图,在中,,于D,如果,且求AB的长.
答案和解析
1.【答案】B
【解答】
解:由图可得
,?
则,
.
2.【答案】B
【解答】
解:如图,作底边上的高AD,
,,AD为高,
则,
,
,
.
3.【答案】B
【解答】
解:如图所示,过点A作于点D,
由题意知,,,米,
设米,
,
米,
在中,,
,
由可得,,
解得:.
4.【答案】D
【解析】解:一艘海轮位于灯塔P的南偏东方向,
,
海里,
海里;
5.【答案】C
【解析】解:设圆锥的母线长为R,由题意得,
解得.
,
6.【答案】A
【解答】
解:,,AB的垂直平分线MN交AC于D,
,
.
,
,
解得,
,
.
7.【答案】D
【解析】解:是直径,
,
的半径是13,
,
由勾股定理得:,
,
,
,
8.【答案】B
【解析】【试题解析】
解:如图,
由题意得:地毯的竖直的线段加起来等于BC,水平的线段相加正好等于AC,
即地毯的总长度至少为,
在中,,,.
,
.
.
9.【答案】B
【解析】解:
、的角平分线分别是BD,CE
,
即;故正确;
若成立,则应有
应有,
即,
此时,
,
而根据题意,没有条件可以说明是,
故错误;
点F是内心,作,
则,
,≌
,故正确;
由于点F是内心而不是各边中线的交点,故BF不一定成立,因此不正确.
因此本题正确的结论为.
10.【答案】B
【解析】解:在中,,
,
.
11.【答案】D
【解析】解:作于C,
在中,,
,
点P的坐标为,
12.【答案】B
【解答】解:中,,,,
,
,
,
,
与AC的位置关系是相切,
故选:B.
13.【答案】C
【解析】解:在山坡上种树,坡度:2,
设,则,
,
解得:,
故AC.
14.【答案】130米
【解答】
解:过C作于F,如图所示:
,
,
,
,,
,
米
故答案为130.
15.【答案】
【解答】
解:与都对,
,
在中,,,
根据勾股定理得:,
则.
故答案为.
16.【答案】
【解析】解:由图知,
锐角的正切值随角度的增大而增大,
,
17.【答案】
【解答】
解:,
,
,
∽,
,
,
,
由勾股定理可知:,
,
故答案为:.
18.【答案】
【解答】
解:四边形ABCD是平行四边形,
,,,
,
,
,
在和中,
≌,
,,
四边形AFED是矩形,
,
在中,,,
,
,
?ABCD的面积.
故答案为.
19.【答案】解:
在中,,,
,
,
,
由勾股定理得:.
20.【答案】解:由折叠的性质可知,≌,
,,
,
,
,
;
如图,过A作于点H,
,,
,
,,
,
.
,
,,
.
21.【答案】解:,可设,得,
,
,
解得,舍去,或,
,,
,
,
;
过点作于点E,
,可设,则,
,
,
解得,舍,或,
,
.
22.【答案】解:在中,
,,
,
,
,
,
由勾股定理得.
一、选择题
在中,,,,则的度数为???
A.
B.
C.
D.
如果一个等腰三角形的底角为,腰长为,那么这个三角形的面积为
A.
B.
C.
D.
如图,从地面B处测得热气球A的仰角为,从地面C处测得热气球A的仰角为若BC为,则热气球A的高度为?
???
A.
B.
C.
D.
如图,一艘海轮位于灯塔P的南偏东方向,距离灯塔40?海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的正东方向上的B处.这时,B处与灯塔P的距离BP的长可以表示为
A.
40海里
B.
海里
C.
海里
D.
海里
已知圆锥的底面半径为5cm,侧面积为,设圆锥的母线与高的夹角为,则的值为
A.
B.
C.
D.
如图,在中,,,AB的垂直平分线MN交AC于D,连接若,则BC的长是?
???
A.
B.
C.
D.
如图,AB是的直径,点C和点D是上位于直径AB两侧的点,连接AC,AD,BD,CD,若的半径是13,,则的值是
A.
B.
C.
D.
如图,在高2m,坡角为的楼梯表面铺地毯地毯的长度至少需要
A.
B.
C.
4m
D.
如图,内接于,的度数为,、的角平分线分别交于AC、AB于点D、E,CE、BD相交于点以下四个结论:;;;其中结论一定正确的序号数是
A.
B.
C.
D.
在中,,,,则直角边BC的长是
A.
B.
C.
D.
如图,以坐标原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是上一点不与A,B重合,连接OP,设,则点P的坐标是
A.
B.
C.
D.
如图,中,,,,以点B为圆心,r为半径作,当时,与AC的位置关系是
A.
相离
B.
相切
C.
相交
D.
无法确定
如图,在山坡上种树,坡度:2,,则相邻两树的水平距离AC为
A.
5m
B.
C.
D.
10m
二、填空题
如图,某河堤的横断面是梯形ABCD,,于点E,米,米,,求AD的长度.
如图,在边长为1的正方形网格中,的圆心在格点上,则________.
如图所示的网格是正方形网格,则______填“”,“”或“”
如图,在中,,于点D,,,则______.
如图,在中,,过点D作于点E,延长CB至点F,使,连接若,,则的面积为________.
三、解答题
在中,,,,解这个直角三角形.
如图,D是的BC边上一点,连接AD,作的外接圆,将沿直线AD折叠,点C的对应点E落在上.
求证:.
若,,,求BC的长.
如图,在中,,D为BC上一点,,,.
求AD的长;
求的值.
如图,在中,,于D,如果,且求AB的长.
答案和解析
1.【答案】B
【解答】
解:由图可得
,?
则,
.
2.【答案】B
【解答】
解:如图,作底边上的高AD,
,,AD为高,
则,
,
,
.
3.【答案】B
【解答】
解:如图所示,过点A作于点D,
由题意知,,,米,
设米,
,
米,
在中,,
,
由可得,,
解得:.
4.【答案】D
【解析】解:一艘海轮位于灯塔P的南偏东方向,
,
海里,
海里;
5.【答案】C
【解析】解:设圆锥的母线长为R,由题意得,
解得.
,
6.【答案】A
【解答】
解:,,AB的垂直平分线MN交AC于D,
,
.
,
,
解得,
,
.
7.【答案】D
【解析】解:是直径,
,
的半径是13,
,
由勾股定理得:,
,
,
,
8.【答案】B
【解析】【试题解析】
解:如图,
由题意得:地毯的竖直的线段加起来等于BC,水平的线段相加正好等于AC,
即地毯的总长度至少为,
在中,,,.
,
.
.
9.【答案】B
【解析】解:
、的角平分线分别是BD,CE
,
即;故正确;
若成立,则应有
应有,
即,
此时,
,
而根据题意,没有条件可以说明是,
故错误;
点F是内心,作,
则,
,≌
,故正确;
由于点F是内心而不是各边中线的交点,故BF不一定成立,因此不正确.
因此本题正确的结论为.
10.【答案】B
【解析】解:在中,,
,
.
11.【答案】D
【解析】解:作于C,
在中,,
,
点P的坐标为,
12.【答案】B
【解答】解:中,,,,
,
,
,
,
与AC的位置关系是相切,
故选:B.
13.【答案】C
【解析】解:在山坡上种树,坡度:2,
设,则,
,
解得:,
故AC.
14.【答案】130米
【解答】
解:过C作于F,如图所示:
,
,
,
,,
,
米
故答案为130.
15.【答案】
【解答】
解:与都对,
,
在中,,,
根据勾股定理得:,
则.
故答案为.
16.【答案】
【解析】解:由图知,
锐角的正切值随角度的增大而增大,
,
17.【答案】
【解答】
解:,
,
,
∽,
,
,
,
由勾股定理可知:,
,
故答案为:.
18.【答案】
【解答】
解:四边形ABCD是平行四边形,
,,,
,
,
,
在和中,
≌,
,,
四边形AFED是矩形,
,
在中,,,
,
,
?ABCD的面积.
故答案为.
19.【答案】解:
在中,,,
,
,
,
由勾股定理得:.
20.【答案】解:由折叠的性质可知,≌,
,,
,
,
,
;
如图,过A作于点H,
,,
,
,,
,
.
,
,,
.
21.【答案】解:,可设,得,
,
,
解得,舍去,或,
,,
,
,
;
过点作于点E,
,可设,则,
,
,
解得,舍,或,
,
.
22.【答案】解:在中,
,,
,
,
,
,
由勾股定理得.
