2020-2021学年人教版九年级数学下册28.1 锐角三角函数同步练习(Word版 含答案)
文档属性
| 名称 | 2020-2021学年人教版九年级数学下册28.1 锐角三角函数同步练习(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 188.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 19:08:02 | ||
图片预览



文档简介
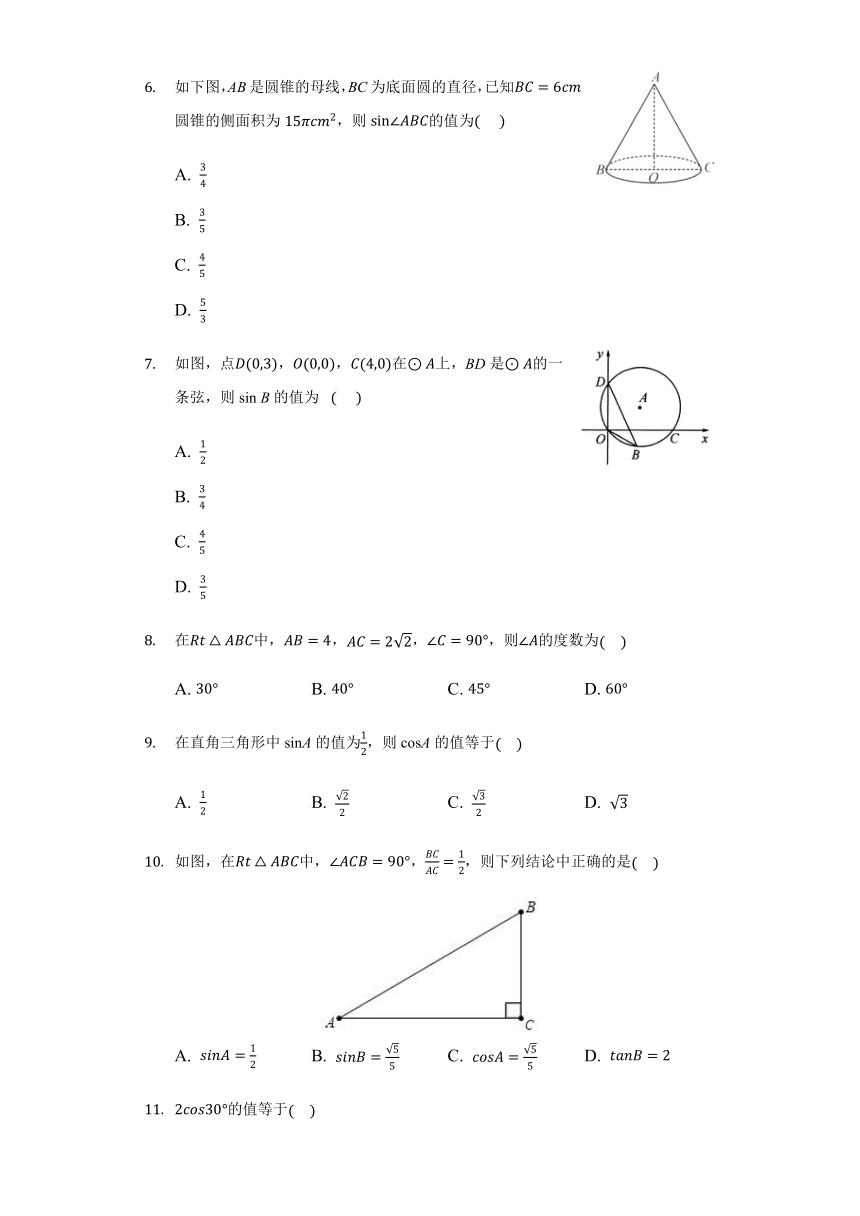
锐角三角函数练习
一、选择题
如图,在中,,,,则等于?
?
?
A.
B.
C.
D.
如果把一个锐角三角形三边的长都扩大为原来的两倍,那么锐角A的正切值?
???
A.
扩大为原来的两倍
B.
缩小为原来的
C.
不变
D.
无法确定
如图,将放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则tanA的值是
A.
B.
C.
2
D.
计算:
A.
B.
2
C.
D.
在中,若,则一定是?
???
A.
锐角三角形
B.
钝角三角形
C.
等边三角形
D.
等腰直角三角形
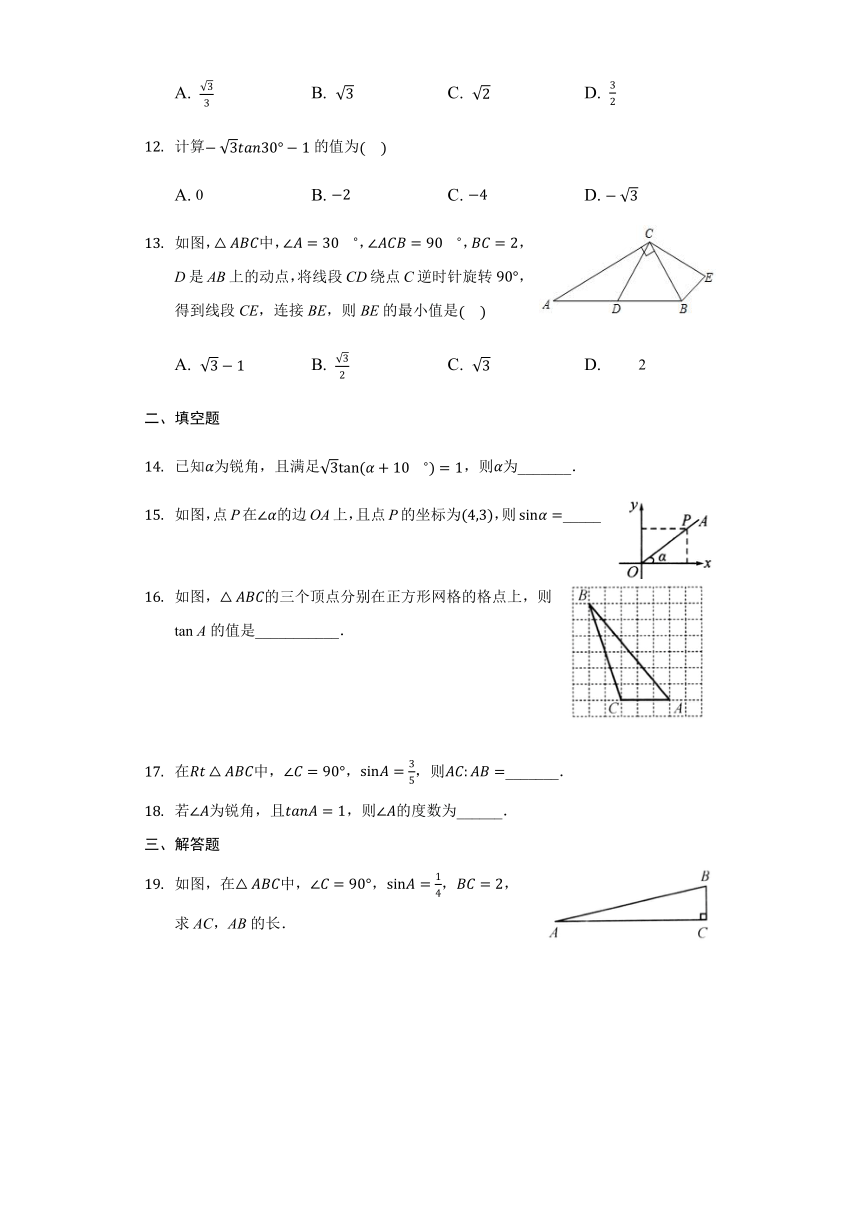
如下图,AB是圆锥的母线,BC为底面圆的直径,已知,圆锥的侧面积为,则的值为???
A.
B.
C.
D.
如图,点,,在上,BD是的一条弦,则sin
B的值为?
???
A.
B.
C.
D.
在中,,,,则的度数为
A.
B.
C.
D.
在直角三角形中sinA的值为,则cosA的值等于
A.
B.
C.
D.
如图,在中,,,则下列结论中正确的是
A.
B.
C.
D.
的值等于
A.
B.
C.
D.
计算的值为
A.
0
B.
C.
D.
如图,中,,,,D是AB上的动点,将线段CD绕点C逆时针旋转,得到线段CE,连接BE,则BE的最小值是
A.
B.
C.
D.
2
二、填空题
已知为锐角,且满足,则为_______.
如图,点P在的边OA上,且点P的坐标为,则_____.
如图,的三个顶点分别在正方形网格的格点上,则tan
A的值是___________.
在中,,,则_______.
若为锐角,且,则的度数为______.
三、解答题
如图,在中,,,,求AC,AB的长.
计算:.
解方程:;
.
答案和解析
1.【答案】A
【解答】
解:由勾股定理得,
.
2.【答案】C
【解答】
解:因为三边的长度都扩大为原来的两倍所得的三角形与原三角形相似,
所以锐角A的大小没改变,所以锐角A的余弦值也不变.
3.【答案】D
【解答】
解:连接BD.
则,,
则.
4.【答案】C
【解析】解:
5.【答案】D
【解答】
解:由,,得
,.
解得,,
则一定是等腰直角三角形,
故选D.
6.【答案】C
【解答】
解:设圆锥的母线长为R,由题意得
,
解得.
圆锥的高为,
,
7.【答案】D
【解答】
解:连结CD,
,,
,,
,
为的直径,且,
,
.
8.【答案】C
【解析】解:在中,,,
,
则.
9.【答案】C
【解答】
解:在直角三角形中sinA的值为,
.
.
10.【答案】D
【解析】解:在中,,,
设,则,故AB,
故,故A选项错误;
,故B选项错误;
,故C选项错误;
,故D选项正确;
11.【答案】B
【解析】解:.
12.【答案】B
【解析】解:原式,
13.【答案】A
【解析】解:如图,过点C作于K,将线段CK绕点C逆时针旋转得到CH,连接HE,延长HE交AB的延长线于J.
,
,
,,
≌,
,
,
四边形CKJH是矩形,
,
四边形CKJH是正方形,
点E在直线HJ上运动,当点E与J重合时,BE的值最小,
在中,,,
,,
,
的最小值为,
14.【答案】
【解答】
解:,
,
,
.
故答案为.
15.【答案】
【解答】
解:如图:
是的边OA上一点,且点P的坐标为,作,
,,
由勾股定理得,
,
故答案为.
16.【答案】
解:如图所示:
在中,,,
则,
故答案为.
17.【答案】4:5
【解答】
解:如图,在中,,,
,
设,,
,
:::5.
故答案为4:5.
18.【答案】
【解析】解:为锐角,且,,
.
19.【答案】解:在中,
,,
.
.
.
20.【答案】解:原式
.
21.【答案】解:,
,
,
或,
,;
原式
.
一、选择题
如图,在中,,,,则等于?
?
?
A.
B.
C.
D.
如果把一个锐角三角形三边的长都扩大为原来的两倍,那么锐角A的正切值?
???
A.
扩大为原来的两倍
B.
缩小为原来的
C.
不变
D.
无法确定
如图,将放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则tanA的值是
A.
B.
C.
2
D.
计算:
A.
B.
2
C.
D.
在中,若,则一定是?
???
A.
锐角三角形
B.
钝角三角形
C.
等边三角形
D.
等腰直角三角形
如下图,AB是圆锥的母线,BC为底面圆的直径,已知,圆锥的侧面积为,则的值为???
A.
B.
C.
D.
如图,点,,在上,BD是的一条弦,则sin
B的值为?
???
A.
B.
C.
D.
在中,,,,则的度数为
A.
B.
C.
D.
在直角三角形中sinA的值为,则cosA的值等于
A.
B.
C.
D.
如图,在中,,,则下列结论中正确的是
A.
B.
C.
D.
的值等于
A.
B.
C.
D.
计算的值为
A.
0
B.
C.
D.
如图,中,,,,D是AB上的动点,将线段CD绕点C逆时针旋转,得到线段CE,连接BE,则BE的最小值是
A.
B.
C.
D.
2
二、填空题
已知为锐角,且满足,则为_______.
如图,点P在的边OA上,且点P的坐标为,则_____.
如图,的三个顶点分别在正方形网格的格点上,则tan
A的值是___________.
在中,,,则_______.
若为锐角,且,则的度数为______.
三、解答题
如图,在中,,,,求AC,AB的长.
计算:.
解方程:;
.
答案和解析
1.【答案】A
【解答】
解:由勾股定理得,
.
2.【答案】C
【解答】
解:因为三边的长度都扩大为原来的两倍所得的三角形与原三角形相似,
所以锐角A的大小没改变,所以锐角A的余弦值也不变.
3.【答案】D
【解答】
解:连接BD.
则,,
则.
4.【答案】C
【解析】解:
5.【答案】D
【解答】
解:由,,得
,.
解得,,
则一定是等腰直角三角形,
故选D.
6.【答案】C
【解答】
解:设圆锥的母线长为R,由题意得
,
解得.
圆锥的高为,
,
7.【答案】D
【解答】
解:连结CD,
,,
,,
,
为的直径,且,
,
.
8.【答案】C
【解析】解:在中,,,
,
则.
9.【答案】C
【解答】
解:在直角三角形中sinA的值为,
.
.
10.【答案】D
【解析】解:在中,,,
设,则,故AB,
故,故A选项错误;
,故B选项错误;
,故C选项错误;
,故D选项正确;
11.【答案】B
【解析】解:.
12.【答案】B
【解析】解:原式,
13.【答案】A
【解析】解:如图,过点C作于K,将线段CK绕点C逆时针旋转得到CH,连接HE,延长HE交AB的延长线于J.
,
,
,,
≌,
,
,
四边形CKJH是矩形,
,
四边形CKJH是正方形,
点E在直线HJ上运动,当点E与J重合时,BE的值最小,
在中,,,
,,
,
的最小值为,
14.【答案】
【解答】
解:,
,
,
.
故答案为.
15.【答案】
【解答】
解:如图:
是的边OA上一点,且点P的坐标为,作,
,,
由勾股定理得,
,
故答案为.
16.【答案】
解:如图所示:
在中,,,
则,
故答案为.
17.【答案】4:5
【解答】
解:如图,在中,,,
,
设,,
,
:::5.
故答案为4:5.
18.【答案】
【解析】解:为锐角,且,,
.
19.【答案】解:在中,
,,
.
.
.
20.【答案】解:原式
.
21.【答案】解:,
,
,
或,
,;
原式
.
