27.2 相似三角形同步练习(Word版 含答案)
文档属性
| 名称 | 27.2 相似三角形同步练习(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 290.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 19:12:13 | ||
图片预览




文档简介
相似三角形练习
一、选择题
如果两个相似三角形对应边之比是1:3,那么它们的对应中线之比是
A.
1:3
B.
1:4
C.
1:6
D.
1:9
如图,在中,两条中线BE、CD相交于点O,则:
A.
2
B.
C.
D.
如下图,,若,,,则AB的长是???
A.
2
B.
3
C.
4
D.
5
如图,已知,则下列四个三角形中,与相似的是?
???
A.
B.
C.
D.
如下图,能保证与相似的条件是???
A.
B.
C.
D.
数学兴趣小组的同学们想利用树影测量树高.课外活动时他们在阳光下测得一根长为1米的竹竿的影子是米,同一时刻测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的台阶上,且影子的末端刚好落在最后一级台阶的上端C处,他们测得落在地面的影长为米,台阶总的高度为米,台阶水平总宽度为米.则树高为
A.
B.
C.
D.
如图,在中,点D是边AB上的一点,,,,则边AC的长为
A.
2
B.
4
C.
6
D.
8
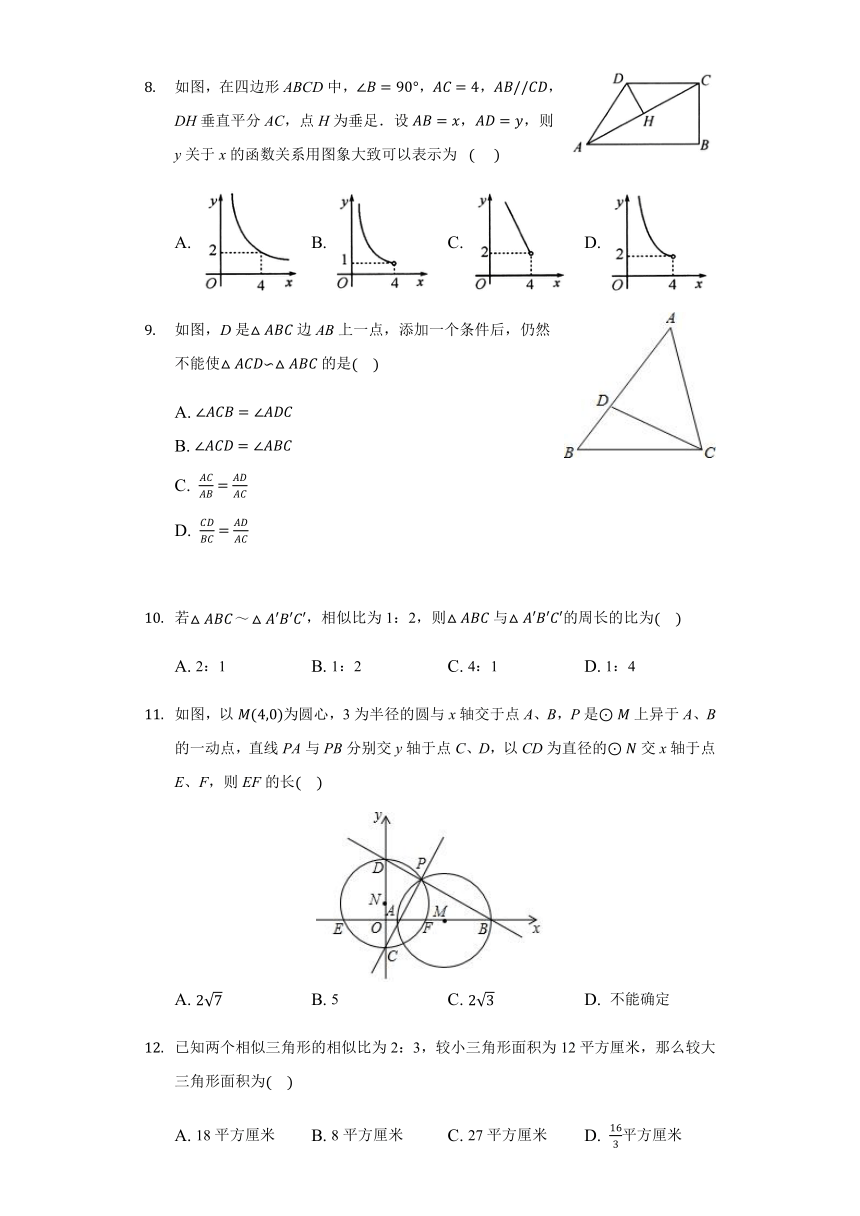
如图,在四边形ABCD中,,,,DH垂直平分AC,点H为垂足.设,,则y关于x的函数关系用图象大致可以表示为?
???
A.
B.
C.
D.
如图,D是边AB上一点,添加一个条件后,仍然不能使∽的是
A.
B.
C.
D.
若,相似比为1:2,则与的周长的比为
A.
2:1
B.
1:2
C.
4:1
D.
1:4
如图,以为圆心,3为半径的圆与x轴交于点A、B,P是上异于A、B的一动点,直线PA与PB分别交y轴于点C、D,以CD为直径的交x轴于点E、F,则EF的长
A.
B.
5
C.
D.
不能确定
已知两个相似三角形的相似比为2:3,较小三角形面积为12平方厘米,那么较大三角形面积为
A.
18平方厘米
B.
8平方厘米
C.
27平方厘米
D.
平方厘米
如图,在矩形ABCD中,,,点E、F在AD边上,BF和CE交于点G,若,则图中阴影部分的面积为
A.
25
B.
30
C.
35
D.
40
若∽,若,则的度数是
A.
B.
C.
D.
二、填空题
如图,在中,,,,则________.
如图,在中,,点D是AC边上的一点,DE垂直平分AB,垂足为点若,,则线段DE的长度为______.
如下图,在等边中,,P为BC边上一点,D为AC边上一点,若,,则________.
如图,A,B是双曲线上的两点,过点A作轴,交OB于点D,垂足为若的面积为1,D为OB的中点,则k的值为______.
三、解答题
如图,,DB平分,过点B作交AD于连接CM交DB于N.
求证:;
若,,求MN的长.
如图,是等边三角形,D为CB延长线上一点,E为BC延长线上一点,且求证:
∽;
.
如图,中,,.
请用尺规作图的方法在AB上找点D,使得保留作图痕迹,不写作法;
在的条件下,求AD的长.
如图,已知:,,,,.
求证:∽.
答案和解析
1.【答案】A
【解析】解:两个相似三角形对应边之比是1:3,
又相似三角形的对应高、中线、角平分线的比等于相似比,
它们的对应中线之比为1:3.
2.【答案】D
【解答】
解:、CD是中的两条中线,
是的中位线,
于是,
∽,
3.【答案】C
【解答】
解:∽,
,
,,,
,
解得:.
4.【答案】C
【解答】
解:由图可知,,,,
,
A.三角形各角的度数分别为,,,
B.三角形各角的度数都是,
C.三角形各角的度数分别为,,,
D.三角形各角的度数分别为,,,
只有C选项中三角形各角的度数与题干中三角形各角的度数相等,
5.【答案】C
【解答】
解:结合条件和图形我们可以找到和中的对应角:和,和,和C.
对应角的对边为对应边,即AD和AC,AE和AB,DE和CB分别为对应边.
相似三角形的对应边成比例,故.
6.【答案】B
【解答】
解:过点C作于点D,如图
,,
.
.
米,
则树高为4米.
7.【答案】B
【解析】解:,,
∽,
,
,
,
,
8.【答案】D
【解答】
解:垂直平分AC,
,,
,
,
,
,,
∽,
,
,
,
,
,
图象是D.
9.【答案】D
【解析】解:A、当时,再由,可得出∽,故此选项不合题意;
B、当时,再由,可得出∽,故此选项不合题意;
C、当时,再由,可得出∽,故此选项不合题意;
D、当时,无法得出∽,故此选项符合题意;
10.【答案】B
【解析】解:,相似比为1:2,
与的周长的比为1:2.
11.【答案】A
【解答】
解:如图示,连接NF,
设圆N半径为r,,则,,
以为圆心、3为半径的圆与x轴交于A、B两点,
,,
是的直径,
直径所对的圆周角是直角,
,
,,
,
,
又,,
,
,
∽,
,
即,
,
,
由垂径定理得:,,
即,
,
12.【答案】C
【解析】解:两个相似三角形的相似比是2:3,
两个相似三角形的面积比是4:9,又较小三角形的面积为12平方厘米,
那么较大三角形的面积为27平方厘米,
13.【答案】C
【解析】解:过点G作于N,延长NG交BC于M,
四边形ABCD是矩形,
,,
,
,
,,
∽,,
:::2,
又,
,,
,
,,
.
14.【答案】A
【解析】解:∽,,
.
15.【答案】6
【解答】
解:,,
∽,
,
,
,
故答案为6.
16.【答案】
【解析】【试题解析】
解:,,,
,
垂直平分AB,
,,
,
又,
∽,
,
即
.
17.【答案】
【解答】
解:由题意得,,
,,
,
∽,
,
,,
,
故答案为.
18.【答案】
【解析】解:如图,过B作轴于E,
轴于C,
与的面积相等,
的面积与梯形CDBE的面积相等,
又,
∽,
为BO的中点,
,即,
解得,
,
即,
解得,
又,
,
19.【答案】证明:平分,
,且,
∽
,
,
又,则
,且,,
,
,
∽
,
又,
20.【答案】证明:是等边三角形,
,,
,,
,
,
,
∽;
由知:∽,
,
,
,
.
21.【答案】解:如图所示,点D即为所求.
∽,
,即,
解得.
22.【答案】证明:,,,.
,,
,
,
∽.
一、选择题
如果两个相似三角形对应边之比是1:3,那么它们的对应中线之比是
A.
1:3
B.
1:4
C.
1:6
D.
1:9
如图,在中,两条中线BE、CD相交于点O,则:
A.
2
B.
C.
D.
如下图,,若,,,则AB的长是???
A.
2
B.
3
C.
4
D.
5
如图,已知,则下列四个三角形中,与相似的是?
???
A.
B.
C.
D.
如下图,能保证与相似的条件是???
A.
B.
C.
D.
数学兴趣小组的同学们想利用树影测量树高.课外活动时他们在阳光下测得一根长为1米的竹竿的影子是米,同一时刻测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的台阶上,且影子的末端刚好落在最后一级台阶的上端C处,他们测得落在地面的影长为米,台阶总的高度为米,台阶水平总宽度为米.则树高为
A.
B.
C.
D.
如图,在中,点D是边AB上的一点,,,,则边AC的长为
A.
2
B.
4
C.
6
D.
8
如图,在四边形ABCD中,,,,DH垂直平分AC,点H为垂足.设,,则y关于x的函数关系用图象大致可以表示为?
???
A.
B.
C.
D.
如图,D是边AB上一点,添加一个条件后,仍然不能使∽的是
A.
B.
C.
D.
若,相似比为1:2,则与的周长的比为
A.
2:1
B.
1:2
C.
4:1
D.
1:4
如图,以为圆心,3为半径的圆与x轴交于点A、B,P是上异于A、B的一动点,直线PA与PB分别交y轴于点C、D,以CD为直径的交x轴于点E、F,则EF的长
A.
B.
5
C.
D.
不能确定
已知两个相似三角形的相似比为2:3,较小三角形面积为12平方厘米,那么较大三角形面积为
A.
18平方厘米
B.
8平方厘米
C.
27平方厘米
D.
平方厘米
如图,在矩形ABCD中,,,点E、F在AD边上,BF和CE交于点G,若,则图中阴影部分的面积为
A.
25
B.
30
C.
35
D.
40
若∽,若,则的度数是
A.
B.
C.
D.
二、填空题
如图,在中,,,,则________.
如图,在中,,点D是AC边上的一点,DE垂直平分AB,垂足为点若,,则线段DE的长度为______.
如下图,在等边中,,P为BC边上一点,D为AC边上一点,若,,则________.
如图,A,B是双曲线上的两点,过点A作轴,交OB于点D,垂足为若的面积为1,D为OB的中点,则k的值为______.
三、解答题
如图,,DB平分,过点B作交AD于连接CM交DB于N.
求证:;
若,,求MN的长.
如图,是等边三角形,D为CB延长线上一点,E为BC延长线上一点,且求证:
∽;
.
如图,中,,.
请用尺规作图的方法在AB上找点D,使得保留作图痕迹,不写作法;
在的条件下,求AD的长.
如图,已知:,,,,.
求证:∽.
答案和解析
1.【答案】A
【解析】解:两个相似三角形对应边之比是1:3,
又相似三角形的对应高、中线、角平分线的比等于相似比,
它们的对应中线之比为1:3.
2.【答案】D
【解答】
解:、CD是中的两条中线,
是的中位线,
于是,
∽,
3.【答案】C
【解答】
解:∽,
,
,,,
,
解得:.
4.【答案】C
【解答】
解:由图可知,,,,
,
A.三角形各角的度数分别为,,,
B.三角形各角的度数都是,
C.三角形各角的度数分别为,,,
D.三角形各角的度数分别为,,,
只有C选项中三角形各角的度数与题干中三角形各角的度数相等,
5.【答案】C
【解答】
解:结合条件和图形我们可以找到和中的对应角:和,和,和C.
对应角的对边为对应边,即AD和AC,AE和AB,DE和CB分别为对应边.
相似三角形的对应边成比例,故.
6.【答案】B
【解答】
解:过点C作于点D,如图
,,
.
.
米,
则树高为4米.
7.【答案】B
【解析】解:,,
∽,
,
,
,
,
8.【答案】D
【解答】
解:垂直平分AC,
,,
,
,
,
,,
∽,
,
,
,
,
,
图象是D.
9.【答案】D
【解析】解:A、当时,再由,可得出∽,故此选项不合题意;
B、当时,再由,可得出∽,故此选项不合题意;
C、当时,再由,可得出∽,故此选项不合题意;
D、当时,无法得出∽,故此选项符合题意;
10.【答案】B
【解析】解:,相似比为1:2,
与的周长的比为1:2.
11.【答案】A
【解答】
解:如图示,连接NF,
设圆N半径为r,,则,,
以为圆心、3为半径的圆与x轴交于A、B两点,
,,
是的直径,
直径所对的圆周角是直角,
,
,,
,
,
又,,
,
,
∽,
,
即,
,
,
由垂径定理得:,,
即,
,
12.【答案】C
【解析】解:两个相似三角形的相似比是2:3,
两个相似三角形的面积比是4:9,又较小三角形的面积为12平方厘米,
那么较大三角形的面积为27平方厘米,
13.【答案】C
【解析】解:过点G作于N,延长NG交BC于M,
四边形ABCD是矩形,
,,
,
,
,,
∽,,
:::2,
又,
,,
,
,,
.
14.【答案】A
【解析】解:∽,,
.
15.【答案】6
【解答】
解:,,
∽,
,
,
,
故答案为6.
16.【答案】
【解析】【试题解析】
解:,,,
,
垂直平分AB,
,,
,
又,
∽,
,
即
.
17.【答案】
【解答】
解:由题意得,,
,,
,
∽,
,
,,
,
故答案为.
18.【答案】
【解析】解:如图,过B作轴于E,
轴于C,
与的面积相等,
的面积与梯形CDBE的面积相等,
又,
∽,
为BO的中点,
,即,
解得,
,
即,
解得,
又,
,
19.【答案】证明:平分,
,且,
∽
,
,
又,则
,且,,
,
,
∽
,
又,
20.【答案】证明:是等边三角形,
,,
,,
,
,
,
∽;
由知:∽,
,
,
,
.
21.【答案】解:如图所示,点D即为所求.
∽,
,即,
解得.
22.【答案】证明:,,,.
,,
,
,
∽.
