1.7.1整式的除法课件(22张)
图片预览







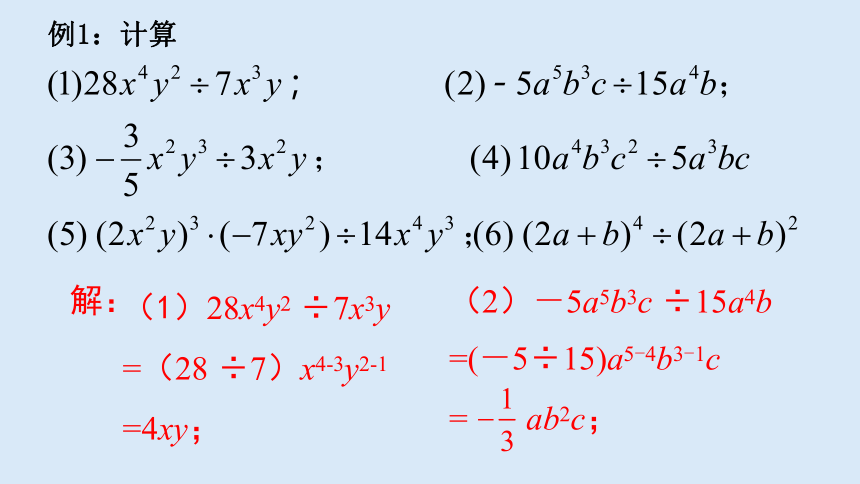
文档简介
(共22张PPT)
第一章
整式的乘除
1.7
整式的除法
北师大版七年级数学下册
学习目标
理解和掌握单项式除以单项式的运算法则,运用运算法则熟练、准确地进行计算.
课前复习
1.同底数幂的除法法则
am÷an
=
am-n
(a≠0,m、n都是正整数,m>n)
同底数幂相除,底数不变,指数相减.
2.快速抢答:
(1)
a20÷a10;
(2)
yz2
z3;
(3)
(?c)4
÷(?c)2;
(4)
2x4
x6.
=
a10
=
yz5
=
c2
=
2x10
?
?
3.单项式乘单项式的运算法则是什么?
你能计算下列各题吗?如果能,说说你的理由.
单项式除以单项式的法则
方法1:利用类似分数约分的方法
约分时,先约系数,再约同底数幂,分子中单独存在的字母及其指数直接作为商的因式.
方法2:利用乘除法的互逆关系
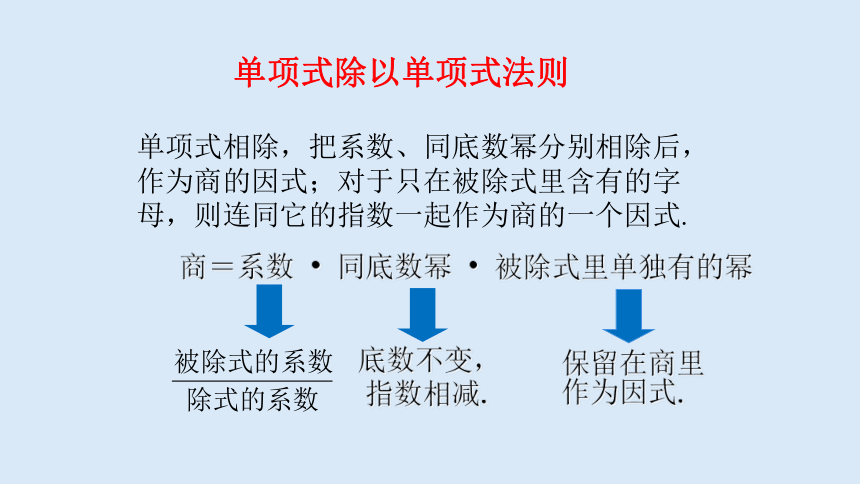
单项式除以单项式法则
单项式相除,把系数、同底数幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连同它的指数一起作为商的一个因式.
底数不变,
指数相减.
保留在商里
作为因式.
商=系数
?
同底数幂
?
被除式里单独有的幂
单项式相乘
单项式相除
第一步
第二步
第三步
系数相乘
系数相除
同底数幂相乘
同底数幂相除
其余字母不变连同其指数作为积的因式
只在被除式里含有的字母连同其指数一起作为商的因式
对比学习
例1:计算
解:
(1)28x4y2
÷7x3y
=(28
÷7)x4-3y2-1
=4xy;
(2)-5a5b3c
÷15a4b
=(-5÷15)a5-4b3-1c
=
ab2c;
例1:计算
解:
例1:计算
解:
注意运算顺序:先乘方,再乘除,最后算加减
可以把
看成一个整体
练习1:下列计算有错吗?错在哪里?应怎样改正?
×
×
×
×
(1)4a8
÷2a
2=
2a
4
(
)
(2)
(
)
(3)(-9x5)
÷(-3x)
=
-3x4
(
)
(4)
(
)
2a6
3x4
2a2bc
(1)解:原式
(2)解:原式
练习2:计算
解:
练习2:计算
练习3、计算
解:(1)原式
注意:单项式的乘方、乘除混合运算要注意运算顺序,先乘方后乘除,有括号的先算括号里面的.
解:(2)原式
练习3、计算
解:(3)原式
注意:乘除混合运算应按从左到右的顺序进行计算
练习3、计算
例2
下雨时,常常是“先见闪电、后闻雷鸣”,这是因为光速比声速快的缘故.已知光在空气中的传播速度为3.0×108米/秒,而声音在空气中的传播速度约300米/秒,你知道光速是声速的多少倍吗?
单项式除以单项式的法则的应用
解:3×108÷300
=3×108÷(3×102)
=106
=1000000
答:光速大约是声速的1000000倍,即100万倍.
例3
若a(xmy4)3÷(3x2yn)2=4x2y2,求a、m、n的值.
解:∵a(xmy4)3÷(3x2yn)2=4x2y2,
∴ax3my12÷9x4y2n=4x2y2,
∴a÷9=4,3m-4=2,12-2n=2,
解得a=36,m=2,n=5.
题目分析:先利用单项式除以单项式法则计算等式左边的式子,再与等式右边的式子进行比较求解.
随堂练习
C
2.计算12a5b4c4÷(-3a2b2c)÷2a3b2c3,其结果正确的
是(
)
A.-2
B.0
C.1
D.2
A
A
1.单项式除法法则
单项式相除,把系数,同底数幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连同它的指数一起作为商的因式.
2.在运算过程中注意数学方法和数学思想的应用,
在实际应用中要把数学问题转化成数学问题
.
课堂小结
注意事项:1.不要遗漏只在被除式中有而除式中没有的字母及字母的指数;
2.系数相除时,应连同它前面的符号一起进行运算.
第一章
整式的乘除
1.7
整式的除法
北师大版七年级数学下册
学习目标
理解和掌握单项式除以单项式的运算法则,运用运算法则熟练、准确地进行计算.
课前复习
1.同底数幂的除法法则
am÷an
=
am-n
(a≠0,m、n都是正整数,m>n)
同底数幂相除,底数不变,指数相减.
2.快速抢答:
(1)
a20÷a10;
(2)
yz2
z3;
(3)
(?c)4
÷(?c)2;
(4)
2x4
x6.
=
a10
=
yz5
=
c2
=
2x10
?
?
3.单项式乘单项式的运算法则是什么?
你能计算下列各题吗?如果能,说说你的理由.
单项式除以单项式的法则
方法1:利用类似分数约分的方法
约分时,先约系数,再约同底数幂,分子中单独存在的字母及其指数直接作为商的因式.
方法2:利用乘除法的互逆关系
单项式除以单项式法则
单项式相除,把系数、同底数幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连同它的指数一起作为商的一个因式.
底数不变,
指数相减.
保留在商里
作为因式.
商=系数
?
同底数幂
?
被除式里单独有的幂
单项式相乘
单项式相除
第一步
第二步
第三步
系数相乘
系数相除
同底数幂相乘
同底数幂相除
其余字母不变连同其指数作为积的因式
只在被除式里含有的字母连同其指数一起作为商的因式
对比学习
例1:计算
解:
(1)28x4y2
÷7x3y
=(28
÷7)x4-3y2-1
=4xy;
(2)-5a5b3c
÷15a4b
=(-5÷15)a5-4b3-1c
=
ab2c;
例1:计算
解:
例1:计算
解:
注意运算顺序:先乘方,再乘除,最后算加减
可以把
看成一个整体
练习1:下列计算有错吗?错在哪里?应怎样改正?
×
×
×
×
(1)4a8
÷2a
2=
2a
4
(
)
(2)
(
)
(3)(-9x5)
÷(-3x)
=
-3x4
(
)
(4)
(
)
2a6
3x4
2a2bc
(1)解:原式
(2)解:原式
练习2:计算
解:
练习2:计算
练习3、计算
解:(1)原式
注意:单项式的乘方、乘除混合运算要注意运算顺序,先乘方后乘除,有括号的先算括号里面的.
解:(2)原式
练习3、计算
解:(3)原式
注意:乘除混合运算应按从左到右的顺序进行计算
练习3、计算
例2
下雨时,常常是“先见闪电、后闻雷鸣”,这是因为光速比声速快的缘故.已知光在空气中的传播速度为3.0×108米/秒,而声音在空气中的传播速度约300米/秒,你知道光速是声速的多少倍吗?
单项式除以单项式的法则的应用
解:3×108÷300
=3×108÷(3×102)
=106
=1000000
答:光速大约是声速的1000000倍,即100万倍.
例3
若a(xmy4)3÷(3x2yn)2=4x2y2,求a、m、n的值.
解:∵a(xmy4)3÷(3x2yn)2=4x2y2,
∴ax3my12÷9x4y2n=4x2y2,
∴a÷9=4,3m-4=2,12-2n=2,
解得a=36,m=2,n=5.
题目分析:先利用单项式除以单项式法则计算等式左边的式子,再与等式右边的式子进行比较求解.
随堂练习
C
2.计算12a5b4c4÷(-3a2b2c)÷2a3b2c3,其结果正确的
是(
)
A.-2
B.0
C.1
D.2
A
A
1.单项式除法法则
单项式相除,把系数,同底数幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连同它的指数一起作为商的因式.
2.在运算过程中注意数学方法和数学思想的应用,
在实际应用中要把数学问题转化成数学问题
.
课堂小结
注意事项:1.不要遗漏只在被除式中有而除式中没有的字母及字母的指数;
2.系数相除时,应连同它前面的符号一起进行运算.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
