1.5.1平方差公式课件（21张）

第一章 整式的乘除
1.5.1 平方差公式
1.经历探索平方差公式的过程，理解并掌握平方差公式的推导和应用；
2.理解平方差公式的结构特征，并能运用公式进行简单的运算.
学习目标
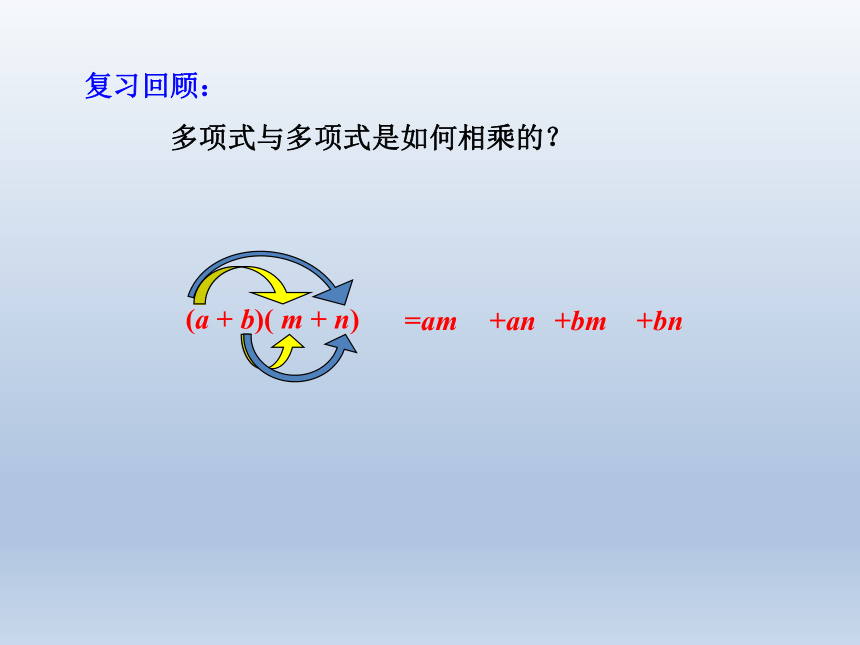
复习回顾：
多项式与多项式是如何相乘的？
(a + b)( m + n)
=am
+an
+bm
+bn
知识点1：平方差公式
计算下列各题
(1) (x+2) (x－2)；
(2) (1+3a) (1－3a )；
(3) (x+5y) (x－5y)；
(4)(2y+z) (2y－z) .
观察以上算式及其运算结果，你有什么发现？
知识点1：平方差公式
计算下列各题
(1) (x+2) (x－2) =x2 － 4
(2) (1+3a) (1－3a )=1－9a2
(3) (x+5y) (x－5y)=x2－25y2
(4)(2y+z) (2y－z) =4y2－z2
观察以上算式及其运算结果，你有什么发现？
=x2 － 22
=1－（3a）2
=x2－（5y）2
=(2y)2－z2
两数和与这两数差的积,等于这两数的平方的差.
平方差公式：
(a+b)(a-b)= .
平方差
a2-b2
文字语言：两个数的和与这两个数的差的积，等于
这两个数的 .
用自己的语言叙述这个式子.
如何推导这个式子呢？
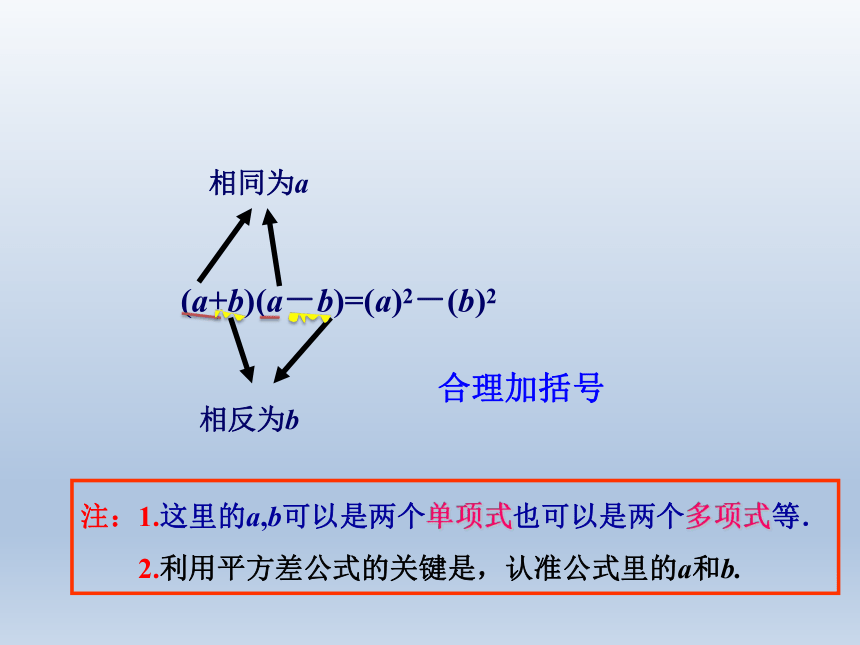
(a+b)(a－b)=(a)2－(b)2
相同为a
相反为b
注：1.这里的a,b可以是两个单项式也可以是两个多项式等．
2.利用平方差公式的关键是，认准公式里的a和b.
合理加括号
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
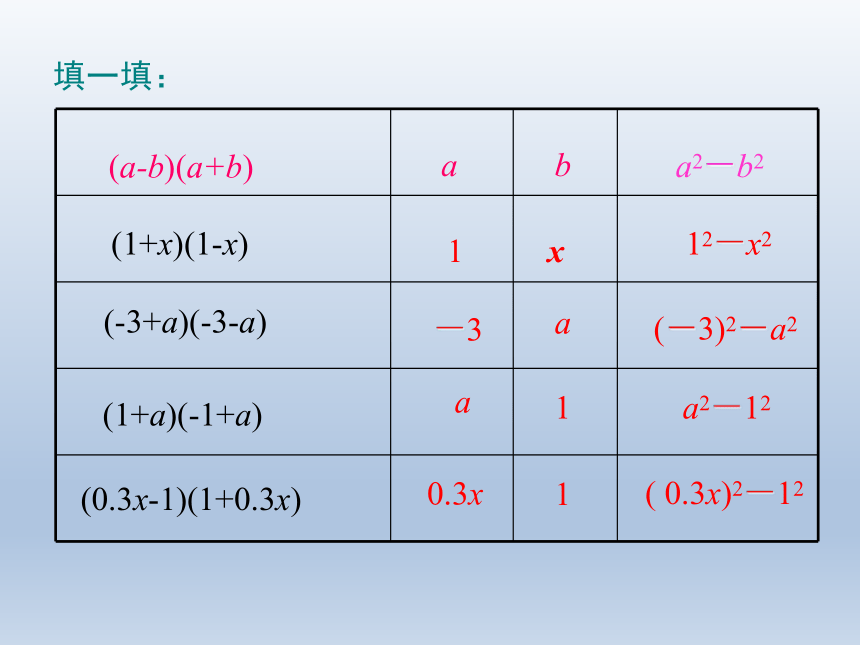
填一填：

a
b
a2－b2
1
x
－3
a
12－x2
(－3)2－a2
a
1
a2－12
0.3x
1
( 0.3x)2－12
(a-b)(a+b)
例1 利用平方差公式计算：
(1) (5+6x)(5－6x)；(2) (x－2y)(x+2y)；
(3) (－m+n)(－m－n) .
解：(1) (5+6x)(5－6x)= 52－(6x)2=25－36x2；
(2) (x－2y)(x+2y)= x2－(2y)2= x2－4y2 ；
(3) (－m+n)(－m－n) = (－m)2－n2 = m2－n2 .
例2 利用平方差公式计算：
(1) (5+6x)(5－6x)；(2) (x－2y)(x+2y)；
(3) (－m+n)(－m－n) .
解：(1) (5+6x)(5－6x)= 52－(6x)2=25－36x2；
(2) (x－2y)(x+2y)= x2－(2y)2= x2－4y2 ；
(3) (－m+n)(－m－n) = (－m)2－n2 = m2－n2 .
注：利用平方差公式的关键是，认准公式里的a和b;
符号相同的为a,符号相反的为b.
例2 观察下面两幅图，你能根据此图从几何的角度推导出平方差公式吗？
①
②
平方差公式常见变形（重要）
1.下列计算能运用平方差公式的是(　　)
A．(m＋n)(－m－n) B．(2x＋3)(3x－2)
C．(5a2－b2c)(bc2＋5a2)
D. ( m2－ n3)(－ m2－ n3)
D
2.下列运算正确的是(　　)
A．x3＋x5＝x8
B．x3＋x5＝x15
C．(x＋1)(x－1)＝x2－1
D．(2x)5＝2x5
C
3.计算：
(1) (a+2) (a－2)； (2) (3a+2b) (3a－2b)；
(3) (－x －1) (1－x) ；(4) (－4k+3) (－4k－3).
(1)(a＋2)(a－2)＝a2－22＝a2－4.
(2)(3a＋2b)(3a－2b)＝(3a)2－(2b)2＝9a2－4b2.
(3)(－x－1)(1－x)＝(－x－1)(－x＋1)
＝(－x)2－12＝x2－1.
(4)(－4k＋3)(－4k－3)＝(－4k)2－32＝16k2－9.
解：
3.(x+1)(x2+1)(x4+1)(x-1)＝_________．
x8-1
C
4.下列运算正确的是(　　)
A．3x＋2y＝5xy
B．(m2)3＝m5
C．(a＋1)(a－1)＝a2－1
D. ＝2
5.若(2x＋3y)(mx－ny)＝9y2－4x2，则(　　)
A．m＝2，n＝3 　　　
B．m＝－2，n＝－3
C．m＝2，n＝－3 　　
D．m＝－2，n＝3
B
6.如图①，在边长为a的正方形中剪去一个边长为b的小正方形(a＞b)，把剩下部分沿虚线剪开拼成一个梯形(如图②)，利用这两个图形的面积，可以验证的公式是(　　)
A．a2＋b2＝(a＋b)(a－b)
B．a2－b2＝(a＋b)(a－b)
C．(a＋b)2＝a2＋2ab＋b2
D．(a－b)2＝a2－2ab＋b2
B
3.已知x2-4y2=12,x+2y=4,求x-2y的值．
能力提升
1.已知a＋b＝3，a－b＝1，则a2－b2的值为___．
2.若x，y满足|x＋y＋5|＋(x－y－9)2＝0，则x2－y2的值为(　　)
A．14 B．－14 C．45 D．－45
4.计算 ．
能力提升
1.已知a＋b＝3，a－b＝1，则a2－b2的值为___．
3
2.若x，y满足|x＋y＋5|＋(x－y－9)2＝0，则x2－y2的值为(　　)
A．14 B．－14 C．45 D．－45
D
3.已知x2-4y2=12,x+2y=4,求x-2y的值．
能力提升
解：∵x2-4y2=（x+2y）（x-2y）,
x2-4y2=12,x+2y=4；
∴12=4（x-2y）
∴x-2y=3．
4.计算 ．
能力提升