1.5.2平方差公式的应用课件(18张)
文档属性
| 名称 | 1.5.2平方差公式的应用课件(18张) |  | |
| 格式 | ppt | ||
| 文件大小 | 809.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 19:12:34 | ||
图片预览






文档简介
(共18张PPT)
1.5.2
1.掌握平方差公式的结构特征,能运用公式进行简
便运算;
2.会用几何图形说明公式的意义,体会数形结合的
思想方法.
学习目标
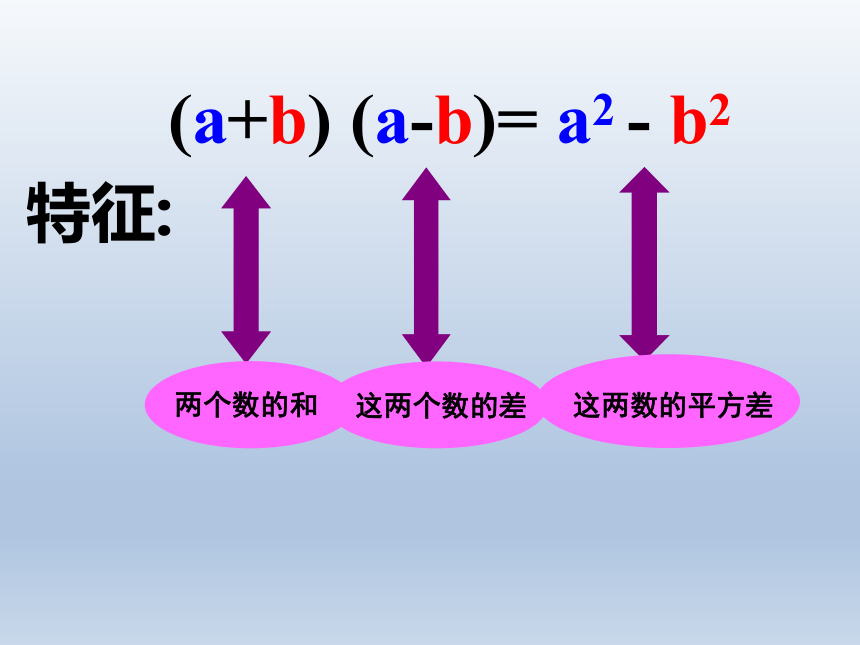
(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,
等于这两个数的平方差。
平方差公式
复习回顾
(a+b)
(a-b)=
a2
-
b2
特征:
两个数的和
这两个数的差
这两数的平方差
(a+b)(a-b)=(a)2-(b)2=a2-b2
相同为a
相反为b
合理加括号
注:1.这里的a,b可以是两个单项式也可以是两个多项式等.
2.利用平方差公式的关键是,认准公式里的a和b.
=4
a2-9;
=4x4-y2.
解原式=(2a+3)(2a-3)
=(2a)2-32
解原式=(-2x2
)2-y2
(1)(3+2a)(-3+2a)
(2)(-2x2-y)(-2x2+y)
利用平方差公式计算:
练习
注意:
运用平方差公式的关键:找到公式中的a和b.
(1)判—找出相同项和相反项;
(2)化—化成公式的标准形式;
(3)套—利用公式计算。
运用公式之前先观察左边式子是否符合平方差公式的特点
平方差公式的应用
(1)计算下列各组算式,并观察它们的共同特点:
(2)从以上的过程中,你发现了什么规律?
(3)请用字母表示这一规律,你能说明它的正确性吗?
7×9=
8×8=
11×13=
12×12=
79×81=
80×80=
例1:
用平方差公式进行计算:
(1)103×97;
(2)
解:(1)原式=(100+3)
(100-3)
=1002-32
=9
991
(2)原式=(173+73)
(173-73)
=246×100
=24600
注意:不能直接应用公式的,要经过变形才可以应用
练习:
运用平方差公式计算:
(1)
2
014×2
016-2
0152;(2)
1.03×0.97;
解:
(1)原式
=(2
015-1)(2
015+1)-2
0152
=2
0152-1-2
0152
=-1;
(2)原式
=(1+0.03)(1-0.03)
=12-0.032
=1-0.000
9
=0.999
1;
例2:计算:
(1)a2(a+b)(a-b)+a2b2;
(2)
(y+2)
(y-2)
–
(y-1)
(y+5)
.
=
y2-4-y2-4y+5
=
-
4y
+
1.
解:(1)原式=a2(a2-b2)+a2b2
=a4-a2b2+a2b2
=a4;
原式=(y2-22)-[y·
y+
y
·5+(-1)·
y+
(-1)×5]
=
y2-4-(y2+4y-5)
(2)
练习:计算:
(1)(3x+4)(3x-4)-(2x+3)(3x-2);
(2)(2x-5)(2x+5)
–2x(2x-3)
.
解:(1)原式=(9x2-16)-(6x2+5x-6)
=9x2-16-6x2-5x+6
=3x2-5x-10.
原式=(2x)2-25-(4x2-6x)
=4x2-25-4x2+6x
=6x-25.
(2)
注:在知识应用中利用了整体思想,根据平方差公式把a+b看成一个整体进行计算.
解:原式=[(a+b)-2c][(a+b)+2c]
=(a+b)2-(2c)2
=a2+ab+ab+b2-4c2
=a2+2ab+b2-4c2
y+z
x-y
x
y
x-z
z
挑战自我
解:原式=[a+(2b-c)][a-(2b-c)]
=a2-(2b-c)2
=a2-(4b2-2bc-2bc+c2)
=a2-4b2+2bc+2bc-c2
=a2-4b2+4bc-c2
练习
计算:(a+2b-c)(a-2b+c)
C
小试牛刀
2.若A=(2+1)(22+1)(24+1),则A的值是______.
解析:A=(2+1)(22+1)(24+1)
=[(2-1)(2+1)(22+1)(24+1)]÷(2-1)
=[(22-1)(22+1)(24+1)]÷(2-1)
=[(24-1)(24+1)]÷(2-1)
=(28-1)÷(2-1)
=28-1.
28-1
能力拓展:
1.(x-y)(x+y)(x2+y2);
解:原式=(x2-y2)(x2+y2)=x4-y4;
作业
1.5.2
1.掌握平方差公式的结构特征,能运用公式进行简
便运算;
2.会用几何图形说明公式的意义,体会数形结合的
思想方法.
学习目标
(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,
等于这两个数的平方差。
平方差公式
复习回顾
(a+b)
(a-b)=
a2
-
b2
特征:
两个数的和
这两个数的差
这两数的平方差
(a+b)(a-b)=(a)2-(b)2=a2-b2
相同为a
相反为b
合理加括号
注:1.这里的a,b可以是两个单项式也可以是两个多项式等.
2.利用平方差公式的关键是,认准公式里的a和b.
=4
a2-9;
=4x4-y2.
解原式=(2a+3)(2a-3)
=(2a)2-32
解原式=(-2x2
)2-y2
(1)(3+2a)(-3+2a)
(2)(-2x2-y)(-2x2+y)
利用平方差公式计算:
练习
注意:
运用平方差公式的关键:找到公式中的a和b.
(1)判—找出相同项和相反项;
(2)化—化成公式的标准形式;
(3)套—利用公式计算。
运用公式之前先观察左边式子是否符合平方差公式的特点
平方差公式的应用
(1)计算下列各组算式,并观察它们的共同特点:
(2)从以上的过程中,你发现了什么规律?
(3)请用字母表示这一规律,你能说明它的正确性吗?
7×9=
8×8=
11×13=
12×12=
79×81=
80×80=
例1:
用平方差公式进行计算:
(1)103×97;
(2)
解:(1)原式=(100+3)
(100-3)
=1002-32
=9
991
(2)原式=(173+73)
(173-73)
=246×100
=24600
注意:不能直接应用公式的,要经过变形才可以应用
练习:
运用平方差公式计算:
(1)
2
014×2
016-2
0152;(2)
1.03×0.97;
解:
(1)原式
=(2
015-1)(2
015+1)-2
0152
=2
0152-1-2
0152
=-1;
(2)原式
=(1+0.03)(1-0.03)
=12-0.032
=1-0.000
9
=0.999
1;
例2:计算:
(1)a2(a+b)(a-b)+a2b2;
(2)
(y+2)
(y-2)
–
(y-1)
(y+5)
.
=
y2-4-y2-4y+5
=
-
4y
+
1.
解:(1)原式=a2(a2-b2)+a2b2
=a4-a2b2+a2b2
=a4;
原式=(y2-22)-[y·
y+
y
·5+(-1)·
y+
(-1)×5]
=
y2-4-(y2+4y-5)
(2)
练习:计算:
(1)(3x+4)(3x-4)-(2x+3)(3x-2);
(2)(2x-5)(2x+5)
–2x(2x-3)
.
解:(1)原式=(9x2-16)-(6x2+5x-6)
=9x2-16-6x2-5x+6
=3x2-5x-10.
原式=(2x)2-25-(4x2-6x)
=4x2-25-4x2+6x
=6x-25.
(2)
注:在知识应用中利用了整体思想,根据平方差公式把a+b看成一个整体进行计算.
解:原式=[(a+b)-2c][(a+b)+2c]
=(a+b)2-(2c)2
=a2+ab+ab+b2-4c2
=a2+2ab+b2-4c2
y+z
x-y
x
y
x-z
z
挑战自我
解:原式=[a+(2b-c)][a-(2b-c)]
=a2-(2b-c)2
=a2-(4b2-2bc-2bc+c2)
=a2-4b2+2bc+2bc-c2
=a2-4b2+4bc-c2
练习
计算:(a+2b-c)(a-2b+c)
C
小试牛刀
2.若A=(2+1)(22+1)(24+1),则A的值是______.
解析:A=(2+1)(22+1)(24+1)
=[(2-1)(2+1)(22+1)(24+1)]÷(2-1)
=[(22-1)(22+1)(24+1)]÷(2-1)
=[(24-1)(24+1)]÷(2-1)
=(28-1)÷(2-1)
=28-1.
28-1
能力拓展:
1.(x-y)(x+y)(x2+y2);
解:原式=(x2-y2)(x2+y2)=x4-y4;
作业
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
