18.1.2平行四边形的判定 课件(21张)
文档属性
| 名称 | 18.1.2平行四边形的判定 课件(21张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 888.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 00:00:00 | ||
图片预览


文档简介
18.1.2 平行四边形的判定(2)
人教版数学八年级下册
A
B
C
D
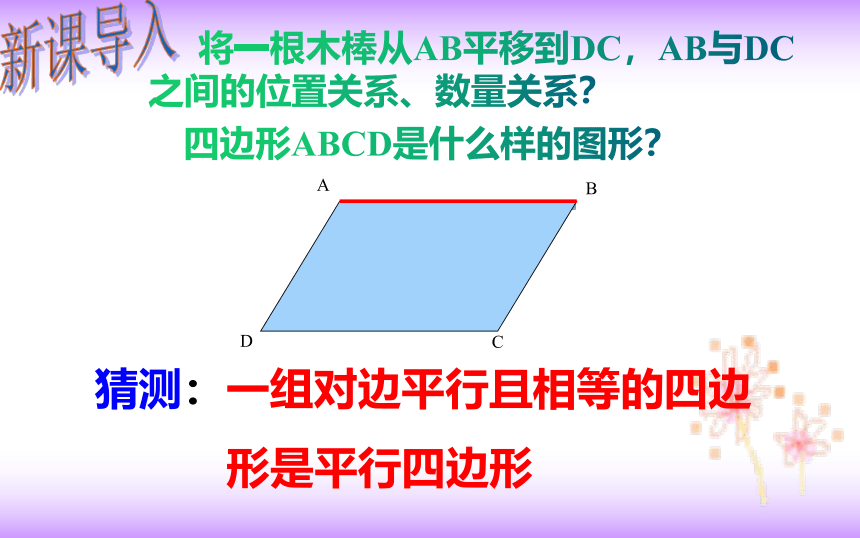
猜测:一组对边平行且相等的四边
形是平行四边形
将一根木棒从AB平移到DC,AB与DC 之间的位置关系、数量关系?
四边形ABCD是什么样的图形?
新课导入
A
B
C
D
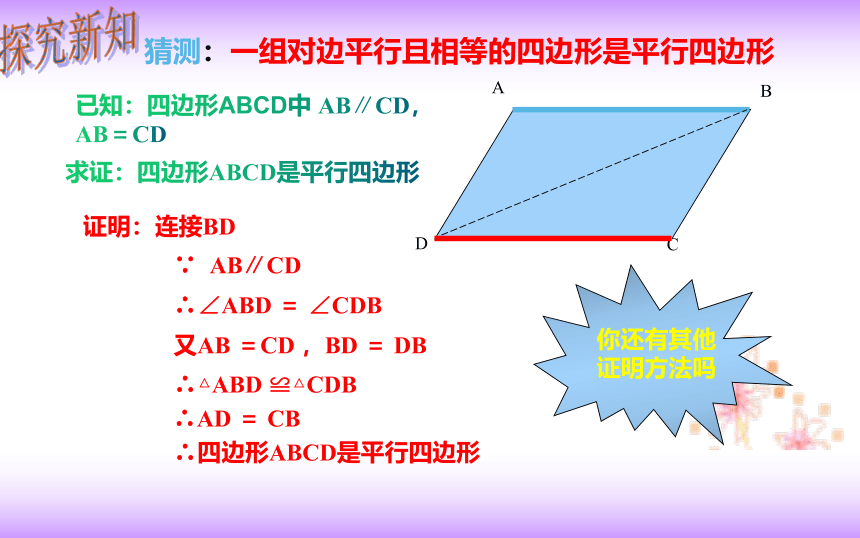
猜测:一组对边平行且相等的四边形是平行四边形
已知:四边形ABCD中 AB∥CD, AB=CD
求证:四边形ABCD是平行四边形
证明:连接BD
∵ AB∥CD
∴∠ABD = ∠CDB
又AB =CD ,BD = DB
∴△ABD ≌△CDB
∴AD = CB
∴四边形ABCD是平行四边形
你还有其他证明方法吗
探究新知
平行四边形的判定定理4:
一组对边平行且相等的四边形是平行四边形.
几何语言描述:
在四边形ABCD中,∵
B
D
A
C
AB=CD,
∴四边形ABCD是平行四边形.
AB∥CD,
探究新知
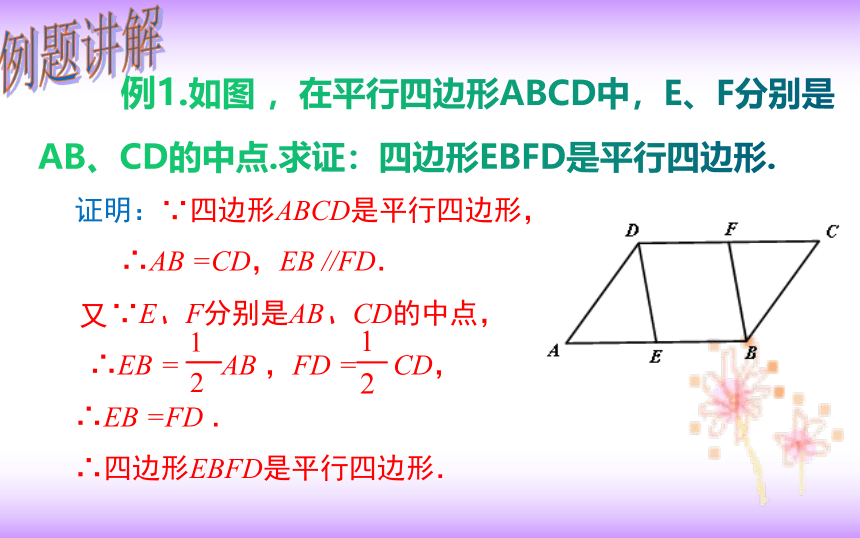
例1.如图 ,在平行四边形ABCD中,E、F分别是AB、CD的中点.求证:四边形EBFD是平行四边形.
证明:∵四边形ABCD是平行四边形,
∵E、F分别是AB、CD的中点,
∴EB = AB ,FD = CD,
∴EB =FD .
∴四边形EBFD是平行四边形.
∴AB =CD,EB //FD.
又
例题讲解
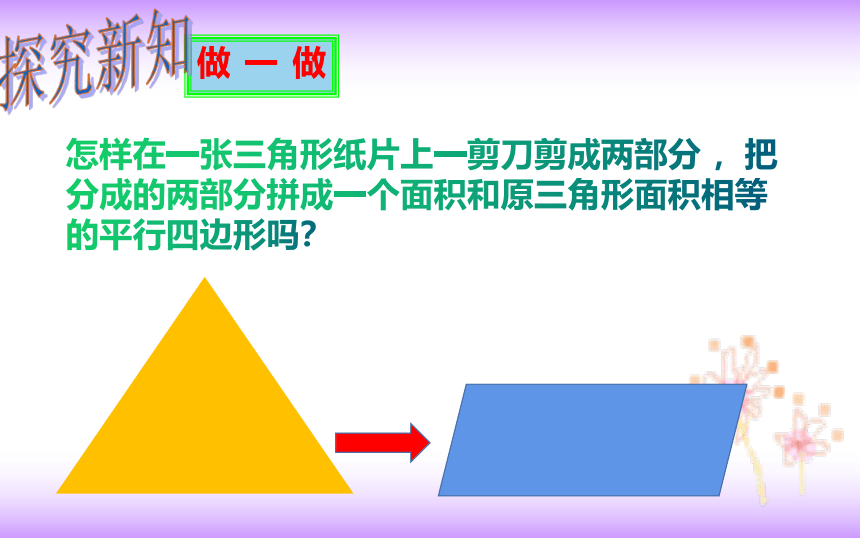
怎样在一张三角形纸片上一剪刀剪成两部分 ,把分成的两部分拼成一个面积和原三角形面积相等的平行四边形吗?
做 一 做
探究新知
A
B
C
D
E
A
E
D
C
B
F
C
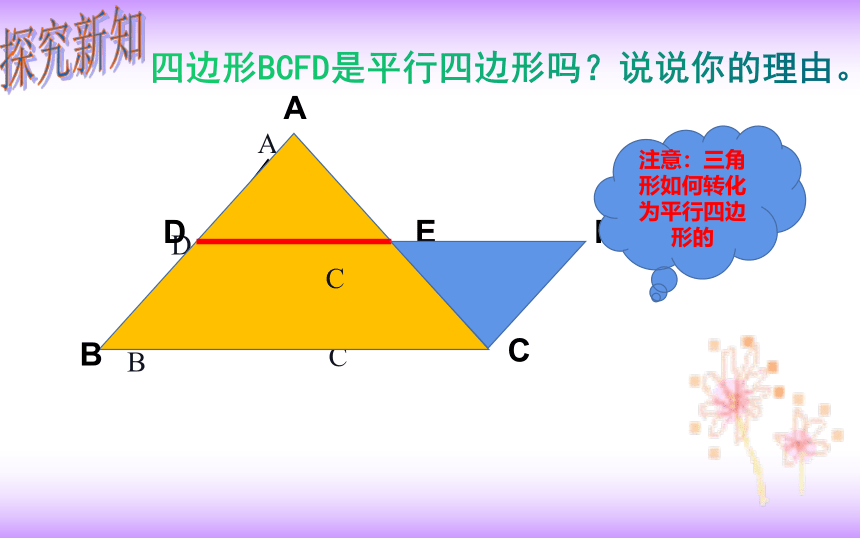
四边形BCFD是平行四边形吗?说说你的理由。
探究新知
注意:三角形如何转化为平行四边形的
A
E
D
C
B
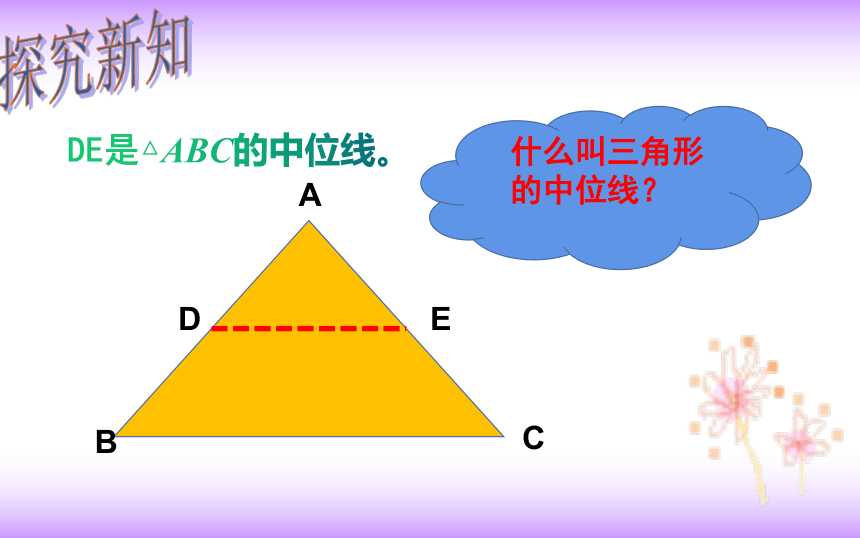
DE是△ABC的中位线。
什么叫三角形的中位线?
探究新知
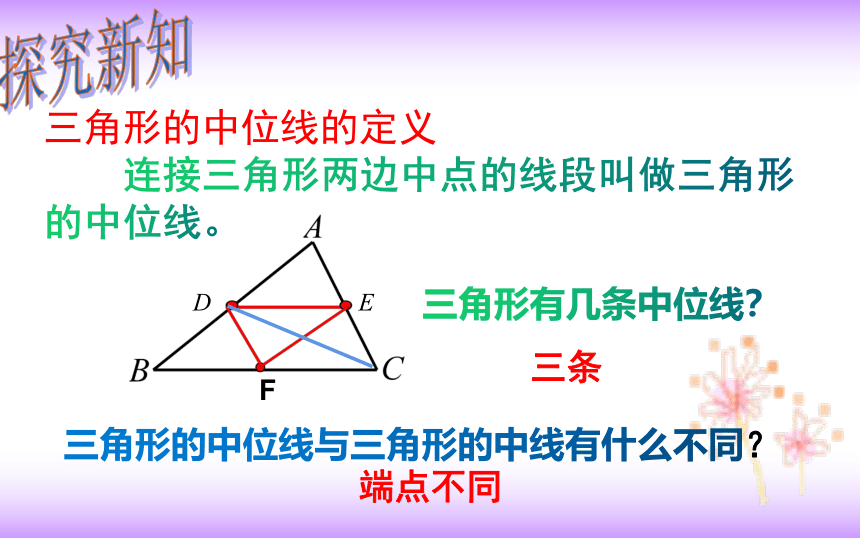
三角形的中位线的定义
连接三角形两边中点的线段叫做三角形的中位线。
D
E
三角形有几条中位线?
三角形的中位线与三角形的中线有什么不同?
三条
端点不同
F
探究新知
E
D
A
C
B
A
E
D
C
B
F
问题1: △ABC中,中位线DE与BC存在什么关系?
DE∥BC
位置关系
数量关系
探究新知
已知:在△ABC 中,DE是△ABC 的中位线
求证:DE ∥ BC,且DE= BC
如 图,延 长DE 到 F,使EF=DE ,
连 结CD, CF, AF.
证明.:
B
C
∵AE=CE, DE=EF
∴四边形ADCF是平行四边形
∴CF DA
∴CF BD
∴四边形ADCF是平行四边形
∴DF BC
又∵DE= DF
∴DE ∥ BC 且 DE= BC
A
C
D
E
F
探究新知
∵DE=EF 、∠AED=∠CEF 、AE=EC
∴△ADE ≌ △CFE
∴AD=FC 、∠A=∠ECF
∴AB∥FC
又AD=DB ∴BD∥= CF
所以 ,四边形BCFD是平行四边形
∴DE ∥ BC 且 DE= BC
已知:在△ABC 中,DE是△ABC 的中位线
求证:DE ∥ BC,且DE= BC
A
C
D
E
F
B
探究新知
证明方法2.:如 图,延 长DE 到 F,使EF=DE
,连 结CF.
三角形中位线定理
三角形的中位线平行且等于第三边的一半.
几何语言:
∵DE是△ABC的中位线
① 证明平行问题
② 证明一条线段是另一条线段的两倍或一半
用 途
A
D
E
B
C
探究新知
例2:如图,A、B两点被池塘隔开,在AB外选一点C,连接AC和BC,并分别找出AC和BC的中点D、E,如果测得DE=20m,那么A、B两点的距离是 _____ m,
理由________________________________________________
40
三角形中位线平行于三角形的第三边,并且等于第三边的一半
解:∵D、E分别是是 AC 、BC的中点
∴DE是△ABC的中位线
∴由三角形的中位线定理:DE∥AB且DE= AB
∴AB=2DE=40cm;
例题讲解
例3 在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.
∴EF∥HG,且EF=HG.
所以四边形EFGH是平行四边形.
解:连结AC.
∵EF是△ABC的一条中位线,
又∵HG是△DAC的一条中位线,
∴EF∥AC,且
∴HG∥AC,且
A
B
C
D
E
F
G
H
例题讲解
1.△ABC中,D、E分别是AB、AC的中点,
BC=10cm,则DE=______.
A
E
D
C
B
(1)
B
D
A
E
C
(2)
2. △ABC中,D、E分别是AB、AC的中点,∠A=50°, ∠B=70°,则∠AED=_____.
5cm
60°
巩固练习
3.已知:如图, E、F分别为AB、AC的中点。
(1)∵ E、F分别为AB、AC的中点。
∴ _____∥____ ,
______=_______ 或______= ______ ? ????
5
12
A
B
C
E
F
EF
EF
BC
BC
2EF
BC
(2)若BC =10cm,则EF =____cm
(3)若EF =6cm, 则BC =__ __cm。
巩固练习
4.如图,点C是AB的中点,AD=CE,CD=BE.
(1)求证:△ACD ≌ △CBE;
(2)求证:四边形CBED是平行四边形.
证明:(1)∵点C是AB的中点,∴AC=BC.
在△ADC与△CEB中,
AD=CE , CD=BE , AC=BC ,
∴△ADC≌△CEB(SSS).
(2)∵△ADC≌△CEB,
∴∠ACD=∠CBE,∴CD∥BE.
又∵CD=BE,
∴四边形CBED是平行四边形.
A
D
C
E
B
巩固练习
两组对边分别平行的四边形是平行四边形
平形四边形的判定
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
边
角
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
对角线
判定一个四边形是平行四边形的方法:
(定义)
三角形中位线定义:连接三角形两边中点的线段叫做三角形的中位线。
三角形中位线性质:三角形的中位线平行于第三边,且等于第三边的一半。
任意四边形四边中点连线所组成的四边形是:平行四边行
课堂小结
布置作业
教科书50页,习 题 18.1 4,6,11题
教科书第60页第3、6题
布置作业
再见
人教版数学八年级下册
A
B
C
D
猜测:一组对边平行且相等的四边
形是平行四边形
将一根木棒从AB平移到DC,AB与DC 之间的位置关系、数量关系?
四边形ABCD是什么样的图形?
新课导入
A
B
C
D
猜测:一组对边平行且相等的四边形是平行四边形
已知:四边形ABCD中 AB∥CD, AB=CD
求证:四边形ABCD是平行四边形
证明:连接BD
∵ AB∥CD
∴∠ABD = ∠CDB
又AB =CD ,BD = DB
∴△ABD ≌△CDB
∴AD = CB
∴四边形ABCD是平行四边形
你还有其他证明方法吗
探究新知
平行四边形的判定定理4:
一组对边平行且相等的四边形是平行四边形.
几何语言描述:
在四边形ABCD中,∵
B
D
A
C
AB=CD,
∴四边形ABCD是平行四边形.
AB∥CD,
探究新知
例1.如图 ,在平行四边形ABCD中,E、F分别是AB、CD的中点.求证:四边形EBFD是平行四边形.
证明:∵四边形ABCD是平行四边形,
∵E、F分别是AB、CD的中点,
∴EB = AB ,FD = CD,
∴EB =FD .
∴四边形EBFD是平行四边形.
∴AB =CD,EB //FD.
又
例题讲解
怎样在一张三角形纸片上一剪刀剪成两部分 ,把分成的两部分拼成一个面积和原三角形面积相等的平行四边形吗?
做 一 做
探究新知
A
B
C
D
E
A
E
D
C
B
F
C
四边形BCFD是平行四边形吗?说说你的理由。
探究新知
注意:三角形如何转化为平行四边形的
A
E
D
C
B
DE是△ABC的中位线。
什么叫三角形的中位线?
探究新知
三角形的中位线的定义
连接三角形两边中点的线段叫做三角形的中位线。
D
E
三角形有几条中位线?
三角形的中位线与三角形的中线有什么不同?
三条
端点不同
F
探究新知
E
D
A
C
B
A
E
D
C
B
F
问题1: △ABC中,中位线DE与BC存在什么关系?
DE∥BC
位置关系
数量关系
探究新知
已知:在△ABC 中,DE是△ABC 的中位线
求证:DE ∥ BC,且DE= BC
如 图,延 长DE 到 F,使EF=DE ,
连 结CD, CF, AF.
证明.:
B
C
∵AE=CE, DE=EF
∴四边形ADCF是平行四边形
∴CF DA
∴CF BD
∴四边形ADCF是平行四边形
∴DF BC
又∵DE= DF
∴DE ∥ BC 且 DE= BC
A
C
D
E
F
探究新知
∵DE=EF 、∠AED=∠CEF 、AE=EC
∴△ADE ≌ △CFE
∴AD=FC 、∠A=∠ECF
∴AB∥FC
又AD=DB ∴BD∥= CF
所以 ,四边形BCFD是平行四边形
∴DE ∥ BC 且 DE= BC
已知:在△ABC 中,DE是△ABC 的中位线
求证:DE ∥ BC,且DE= BC
A
C
D
E
F
B
探究新知
证明方法2.:如 图,延 长DE 到 F,使EF=DE
,连 结CF.
三角形中位线定理
三角形的中位线平行且等于第三边的一半.
几何语言:
∵DE是△ABC的中位线
① 证明平行问题
② 证明一条线段是另一条线段的两倍或一半
用 途
A
D
E
B
C
探究新知
例2:如图,A、B两点被池塘隔开,在AB外选一点C,连接AC和BC,并分别找出AC和BC的中点D、E,如果测得DE=20m,那么A、B两点的距离是 _____ m,
理由________________________________________________
40
三角形中位线平行于三角形的第三边,并且等于第三边的一半
解:∵D、E分别是是 AC 、BC的中点
∴DE是△ABC的中位线
∴由三角形的中位线定理:DE∥AB且DE= AB
∴AB=2DE=40cm;
例题讲解
例3 在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.
∴EF∥HG,且EF=HG.
所以四边形EFGH是平行四边形.
解:连结AC.
∵EF是△ABC的一条中位线,
又∵HG是△DAC的一条中位线,
∴EF∥AC,且
∴HG∥AC,且
A
B
C
D
E
F
G
H
例题讲解
1.△ABC中,D、E分别是AB、AC的中点,
BC=10cm,则DE=______.
A
E
D
C
B
(1)
B
D
A
E
C
(2)
2. △ABC中,D、E分别是AB、AC的中点,∠A=50°, ∠B=70°,则∠AED=_____.
5cm
60°
巩固练习
3.已知:如图, E、F分别为AB、AC的中点。
(1)∵ E、F分别为AB、AC的中点。
∴ _____∥____ ,
______=_______ 或______= ______ ? ????
5
12
A
B
C
E
F
EF
EF
BC
BC
2EF
BC
(2)若BC =10cm,则EF =____cm
(3)若EF =6cm, 则BC =__ __cm。
巩固练习
4.如图,点C是AB的中点,AD=CE,CD=BE.
(1)求证:△ACD ≌ △CBE;
(2)求证:四边形CBED是平行四边形.
证明:(1)∵点C是AB的中点,∴AC=BC.
在△ADC与△CEB中,
AD=CE , CD=BE , AC=BC ,
∴△ADC≌△CEB(SSS).
(2)∵△ADC≌△CEB,
∴∠ACD=∠CBE,∴CD∥BE.
又∵CD=BE,
∴四边形CBED是平行四边形.
A
D
C
E
B
巩固练习
两组对边分别平行的四边形是平行四边形
平形四边形的判定
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
边
角
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
对角线
判定一个四边形是平行四边形的方法:
(定义)
三角形中位线定义:连接三角形两边中点的线段叫做三角形的中位线。
三角形中位线性质:三角形的中位线平行于第三边,且等于第三边的一半。
任意四边形四边中点连线所组成的四边形是:平行四边行
课堂小结
布置作业
教科书50页,习 题 18.1 4,6,11题
教科书第60页第3、6题
布置作业
再见
