2020-2021学年人教版八年级数学下册第18章平行四边形 单元测试卷(Word版 含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册第18章平行四边形 单元测试卷(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 188.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 18:36:27 | ||
图片预览




文档简介
1121410011836400 平行四边形单元测试
选择题
1.在平行四边形ABCD中,∠B=110°,延长AD至F,延长CD至E,连接EF,则∠E+∠F=( )
A.110° B.30° C.50° D.70°
2.在下列条件中,不能够判定一个四边形是平行四边形的是( )
A.一组对边平行,另一组对边相等 B.一组对边平行且相等
C.两组对边分别平行 D.对角线互相平分
3.如图2,在菱形ABCD中,对角线AC=4,∠BAD=120°,则菱形ABCD的周长为()
A.20 B.18 C.16 D.15
4.如图所示,正方形ABCD中,E,F是对角线AC上两点,连接BE,BF,DE,DF,则添加下列哪一个条件可以判定四边形BEDF是菱形( )
A.∠1=∠2 B.BE=DF C.∠EDF=60° D.AB=AF
5.如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
A.8false B.8 C.4false D.6
6.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是()
A.当AB=BC时,它是菱形 B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形 D.当AC=BD时,它是正方形
7.如图,正方形false边长为4,对角线false上有一动点false,过false作false于false,false于false,连结false,则false的最小值为( )
A.false B.2 C.4 D.false
8.如图所示,四边形false、false、false均为平行四边形,其中false、false两点分别在false、false上.若四边形false、false、false的面积分别为false、false、false,则关于false、false、false的大小关系,正确的是( )
A.false B.false C.false D.false
9.如图,正方形ABCD内有两条相交线段MN,EF,M,N,E,F分别在边AB,CD,AD,BC上.小明认为:若MN=EF,则MN⊥EF;小亮认为:若MN⊥EF,则MN=EF,你认为( )
A.仅小明对 B.仅小亮对 C.两人都对 D.两人都不对
10.已知?ABCD中,AD=2AB,F是BC的中点,作AE⊥CD,垂足E在线段CD上,连结EF、AF,下列结论:①2∠BAF=∠BAD;②EF=AF;③S△ABF≤S△AEF;④∠BFE=3∠CEF,中一定成立的是( )
A.①②④ B.①③ C.②③④ D.①②③④
二、填空。
11.矩形的一边长是3.6㎝, 两条对角线的夹角为60?,则矩形对角线长是___________.
12.矩形ABCD中,AB=5,BC=4,将矩形折叠,使得点B落在线段CD的点F处,则线段BE的长为_____________.
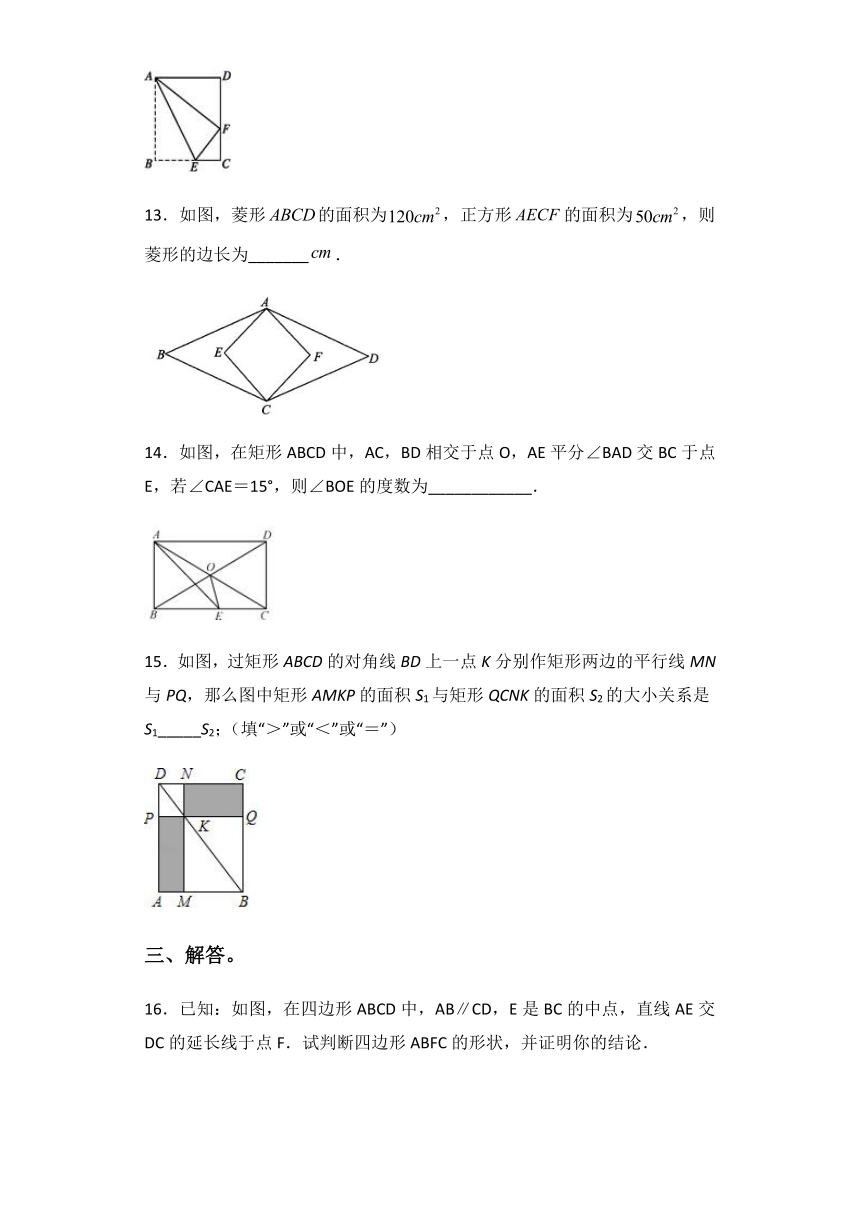
13.如图,菱形false的面积为false,正方形false的面积为false,则菱形的边长为_______false.
14.如图,在矩形ABCD中,AC,BD相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,则∠BOE的度数为____________.
15.如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中矩形AMKP的面积S1与矩形QCNK的面积S2的大小关系是S1_____S2;(填“>”或“<”或“=”)
三、解答。
16.已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.
17.如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E.求证:DA=DE.
18.如图,等腰三角形ABC中,AB=AC,AH垂直BC,点E是AH上一点,延长AH至点F,使FH=EH,
(1)求证:四边形EBFC是菱形;
(2)如果false=false,求证:false.
19.如图,在矩形ABCD中,AB=8cm,BC=16cm,点P从点D出发向点A运动,运动到点A停止,同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
(1)当t为何值时,四边形ABQP是矩形;
(2)当t为何值时,四边形AQCP是菱形;
(3)分别求出(2)中菱形AQCP的周长和面积.
20.如图,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且∠PAE=∠E,PE交CD于点F.
(1)求证:PC=PE;
(2)求∠CPE的度数.
答案
1-5:DACBD
6-10:DADCD
11.7.2cm或cm
12.2.5
13.false;
14.false
15.=
16.四边形ABFC是平行四边形;证明见解析.
【详解】
四边形ABFC是平行四边形;理由如下:
∵AB∥CD,
∴∠BAE=∠CFE,
∵E是BC的中点,
∴BE=CE,
在△ABE和△FCE中, false
∴△ABE≌△FCE(AAS);
∴AB=CF,
又∵AB∥CF,
∴四边形ABFC是平行四边形.
17.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,∴∠E=∠BAE,
∵AE平分∠BAD,∴∠BAE=∠DAE,
∴∠E=∠DAE,
∴DA=DE.
18.(1)证明见解析;(2)证明见解析.
【详解】
证明:(1)∵AB=AC,AH⊥CB,
∴BH=HC.
∵FH=EH,
∴四边形EBFC是平行四边形.
又∵AH⊥CB,
∴四边形EBFC是菱形.
(2)证明:如图,
∵四边形EBFC是菱形.
∴∠2=∠3=false∠ECF.
∵AB=AC,AH⊥CB,
∴∠4=false∠BAC.
∵∠BAC=∠ECF,
∴∠4=∠3.
∵AH⊥CB
∴∠4+∠1+∠2=90°.
∴∠3+∠1+∠2=90°.
即:AC⊥CF.
19.(1)8;(2)6;(3),40cm,80cm2.
【详解】
(1)当四边形ABQP是矩形时,BQ=AP,即:t=16-t,
解得t=8.
答:当t=8时,四边形ABQP是矩形;
(2)设t秒后,四边形AQCP是菱形
当AQ=CQ,即false=16-t时,四边形AQCP为菱形.
解得:t=6.
答:当t=6时,四边形AQCP是菱形;
(3)当t=6时,CQ=10,则周长为:4CQ=40cm,
面积为:10×8=80(cm2).
20.(1)见解析;(2)90°
【详解】
(1)证明:在正方形ABCD中,AD=DC,∠ADP=∠CDP=45°
在△ADP和△CDP中
false
∴△ADP≌△CDP(SAS)
∴PA=PC
∵∠PAE=∠E
∴PA=PE
∴PC=PE
(2)解: 在正方形ABCD中,∠ADC=90°
∴∠EDF=90°
由(1)知,△ADP≌△CDP
∴∠DAP=∠DCP
∵∠DAP=∠E
∴∠DCP=∠E
∵∠CFP=∠EFD(对顶角相等)
∴180°-∠PFC-∠PCF=180°-∠DFE-∠E
即∠CPE=∠EDF=90°
选择题
1.在平行四边形ABCD中,∠B=110°,延长AD至F,延长CD至E,连接EF,则∠E+∠F=( )
A.110° B.30° C.50° D.70°
2.在下列条件中,不能够判定一个四边形是平行四边形的是( )
A.一组对边平行,另一组对边相等 B.一组对边平行且相等
C.两组对边分别平行 D.对角线互相平分
3.如图2,在菱形ABCD中,对角线AC=4,∠BAD=120°,则菱形ABCD的周长为()
A.20 B.18 C.16 D.15
4.如图所示,正方形ABCD中,E,F是对角线AC上两点,连接BE,BF,DE,DF,则添加下列哪一个条件可以判定四边形BEDF是菱形( )
A.∠1=∠2 B.BE=DF C.∠EDF=60° D.AB=AF
5.如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
A.8false B.8 C.4false D.6
6.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是()
A.当AB=BC时,它是菱形 B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形 D.当AC=BD时,它是正方形
7.如图,正方形false边长为4,对角线false上有一动点false,过false作false于false,false于false,连结false,则false的最小值为( )
A.false B.2 C.4 D.false
8.如图所示,四边形false、false、false均为平行四边形,其中false、false两点分别在false、false上.若四边形false、false、false的面积分别为false、false、false,则关于false、false、false的大小关系,正确的是( )
A.false B.false C.false D.false
9.如图,正方形ABCD内有两条相交线段MN,EF,M,N,E,F分别在边AB,CD,AD,BC上.小明认为:若MN=EF,则MN⊥EF;小亮认为:若MN⊥EF,则MN=EF,你认为( )
A.仅小明对 B.仅小亮对 C.两人都对 D.两人都不对
10.已知?ABCD中,AD=2AB,F是BC的中点,作AE⊥CD,垂足E在线段CD上,连结EF、AF,下列结论:①2∠BAF=∠BAD;②EF=AF;③S△ABF≤S△AEF;④∠BFE=3∠CEF,中一定成立的是( )
A.①②④ B.①③ C.②③④ D.①②③④
二、填空。
11.矩形的一边长是3.6㎝, 两条对角线的夹角为60?,则矩形对角线长是___________.
12.矩形ABCD中,AB=5,BC=4,将矩形折叠,使得点B落在线段CD的点F处,则线段BE的长为_____________.
13.如图,菱形false的面积为false,正方形false的面积为false,则菱形的边长为_______false.
14.如图,在矩形ABCD中,AC,BD相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,则∠BOE的度数为____________.
15.如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中矩形AMKP的面积S1与矩形QCNK的面积S2的大小关系是S1_____S2;(填“>”或“<”或“=”)
三、解答。
16.已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.
17.如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E.求证:DA=DE.
18.如图,等腰三角形ABC中,AB=AC,AH垂直BC,点E是AH上一点,延长AH至点F,使FH=EH,
(1)求证:四边形EBFC是菱形;
(2)如果false=false,求证:false.
19.如图,在矩形ABCD中,AB=8cm,BC=16cm,点P从点D出发向点A运动,运动到点A停止,同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
(1)当t为何值时,四边形ABQP是矩形;
(2)当t为何值时,四边形AQCP是菱形;
(3)分别求出(2)中菱形AQCP的周长和面积.
20.如图,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且∠PAE=∠E,PE交CD于点F.
(1)求证:PC=PE;
(2)求∠CPE的度数.
答案
1-5:DACBD
6-10:DADCD
11.7.2cm或cm
12.2.5
13.false;
14.false
15.=
16.四边形ABFC是平行四边形;证明见解析.
【详解】
四边形ABFC是平行四边形;理由如下:
∵AB∥CD,
∴∠BAE=∠CFE,
∵E是BC的中点,
∴BE=CE,
在△ABE和△FCE中, false
∴△ABE≌△FCE(AAS);
∴AB=CF,
又∵AB∥CF,
∴四边形ABFC是平行四边形.
17.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,∴∠E=∠BAE,
∵AE平分∠BAD,∴∠BAE=∠DAE,
∴∠E=∠DAE,
∴DA=DE.
18.(1)证明见解析;(2)证明见解析.
【详解】
证明:(1)∵AB=AC,AH⊥CB,
∴BH=HC.
∵FH=EH,
∴四边形EBFC是平行四边形.
又∵AH⊥CB,
∴四边形EBFC是菱形.
(2)证明:如图,
∵四边形EBFC是菱形.
∴∠2=∠3=false∠ECF.
∵AB=AC,AH⊥CB,
∴∠4=false∠BAC.
∵∠BAC=∠ECF,
∴∠4=∠3.
∵AH⊥CB
∴∠4+∠1+∠2=90°.
∴∠3+∠1+∠2=90°.
即:AC⊥CF.
19.(1)8;(2)6;(3),40cm,80cm2.
【详解】
(1)当四边形ABQP是矩形时,BQ=AP,即:t=16-t,
解得t=8.
答:当t=8时,四边形ABQP是矩形;
(2)设t秒后,四边形AQCP是菱形
当AQ=CQ,即false=16-t时,四边形AQCP为菱形.
解得:t=6.
答:当t=6时,四边形AQCP是菱形;
(3)当t=6时,CQ=10,则周长为:4CQ=40cm,
面积为:10×8=80(cm2).
20.(1)见解析;(2)90°
【详解】
(1)证明:在正方形ABCD中,AD=DC,∠ADP=∠CDP=45°
在△ADP和△CDP中
false
∴△ADP≌△CDP(SAS)
∴PA=PC
∵∠PAE=∠E
∴PA=PE
∴PC=PE
(2)解: 在正方形ABCD中,∠ADC=90°
∴∠EDF=90°
由(1)知,△ADP≌△CDP
∴∠DAP=∠DCP
∵∠DAP=∠E
∴∠DCP=∠E
∵∠CFP=∠EFD(对顶角相等)
∴180°-∠PFC-∠PCF=180°-∠DFE-∠E
即∠CPE=∠EDF=90°
