18.2特殊的平行四边形 培优训练卷(Word版 含答案)
文档属性
| 名称 | 18.2特殊的平行四边形 培优训练卷(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 403.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 00:00:00 | ||
图片预览



文档简介
《特殊的平行四边形》同步培优训练
选择题
1.如图,在△ABC中,点D在BC上,DE∥AC,DF∥AB,下列四个判断中不正确的是( )
A.四边形AEDF是平行四边形
B.若∠BAC=90°,则四边形AEDF是矩形
C.若AD平分∠BAC,则四边形AEDF是矩形
D.若AD⊥BC且AB=AC,则四边形AEDF是菱形
2.如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF=( )
A.30° B.45° C.55° D.60°
3.如图,在菱形false中,点false在边false上,false.若false,则边false的长为( )
A.false B.false C.false D.false
4.已知在四边形ABCD中,对角线AC与BD相交于点O,false,下列判断中错误的是( )
A.如果false,false,那么四边形ABCD是平行四边形
B.如果false,false,那么四边形ABCD是矩形
C.如果false,false,那么四边形ABCD是菱形
D.如果false,AC垂直平分BD,那么四边形ABCD是正方形
5.如图,将一张长方形纸片ABCD按图中方式折叠,若AE=3,AB=4,BE=5,则重叠部分的面积为( )
A.6 B.8 C.10 D.12
6.如图,在菱形ABCD中,AB=5,对角线AC与BD相交于点O,且AC:BD=3:4,AE⊥CD于点E,则AE的长是( )
A.4 B.245 C.5 D.125
7.在四边形false中,false,如果再添加一个条件,即可推出该四边形是正方形,这个条件可以是( )
A.false B.false C.false D.false
8.如图所示,矩形ABCD中,AE平分false交BC于E,false,则下面的结论:①false是等边三角形;②false;③false;④false,其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
9.如图,在菱形false中,false,false的垂直平分线交对角线false于点false,false为垂足,连结false,则false等于( )
A.30° B.35° C.40° D.45°
10.如图,菱形false中,过顶点false作false交对角线false于false点,已知false,则false的大小为( )
A.false B.false C.false D.false
二、填空。
11.如图,在正方形ABCD的外侧,作等边△ADE,则∠AEB=_______
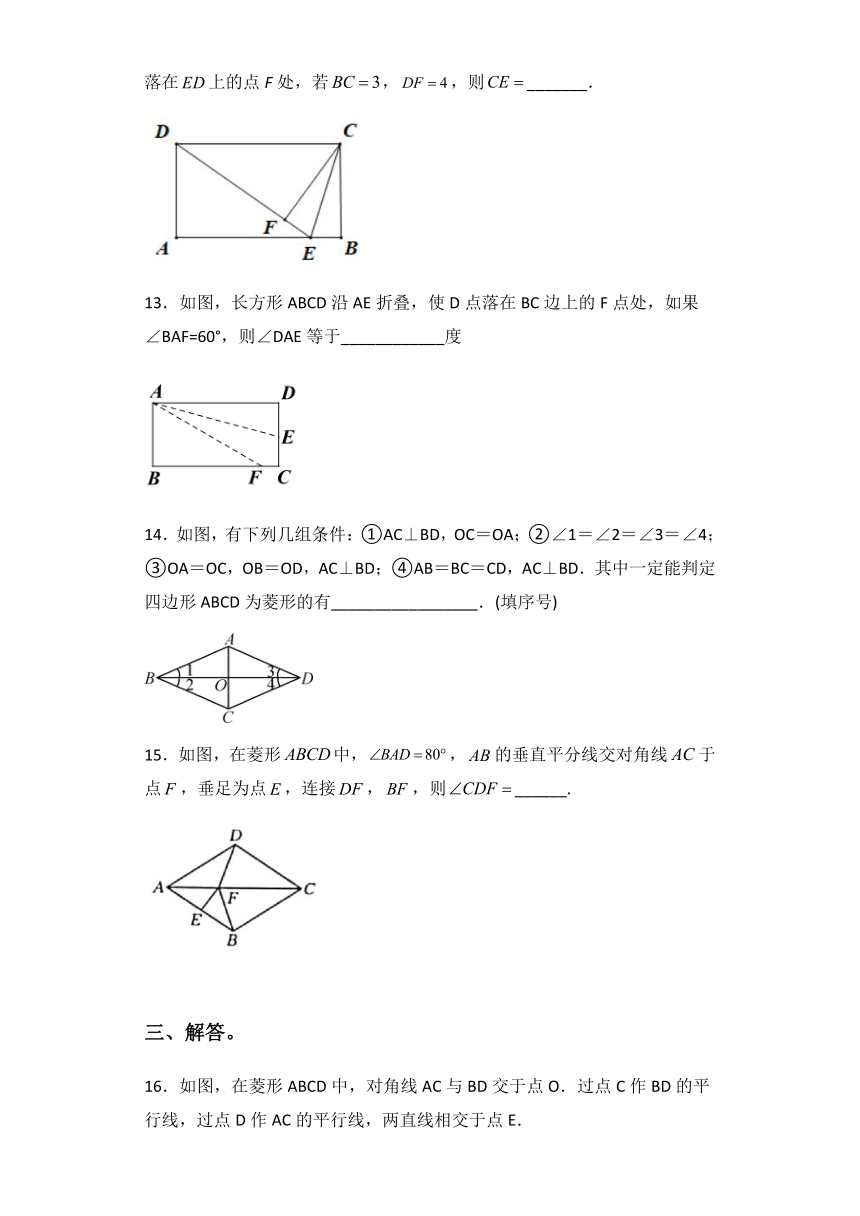
12.如图,E为矩形false的边false上一点,将矩形沿false折叠,使点B恰好落在false上的点F处,若false,false,则false_______.
13.如图,长方形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠BAF=60°,则∠DAE等于____________度
14.如图,有下列几组条件:①AC⊥BD,OC=OA;②∠1=∠2=∠3=∠4;③OA=OC,OB=OD,AC⊥BD;④AB=BC=CD,AC⊥BD.其中一定能判定四边形ABCD为菱形的有_________________.(填序号)
15.如图,在菱形false中,false,false的垂直平分线交对角线false于点false,垂足为点false,连接false,false,则false______.
三、解答。
16.如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
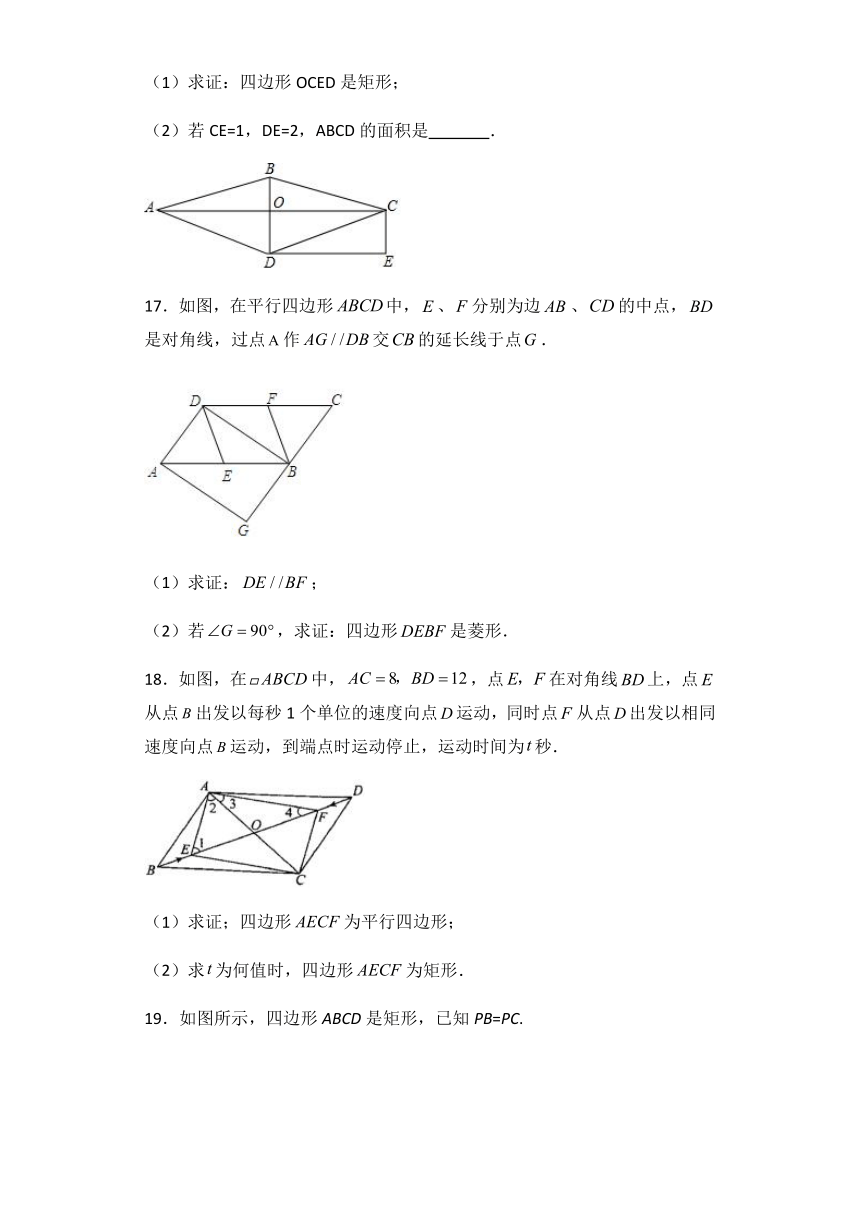
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面积是 .
17.如图,在平行四边形false中,false、false分别为边false、false的中点,false是对角线,过点false作false交false的延长线于点false.
(1)求证:false;
(2)若false,求证:四边形false是菱形.
18.如图,在false中,false,点false在对角线false上,点false从点false出发以每秒1个单位的速度向点false运动,同时点false从点false出发以相同速度向点false运动,到端点时运动停止,运动时间为false秒.
(1)求证;四边形false为平行四边形;
(2)求false为何值时,四边形false为矩形.
19.如图所示,四边形ABCD是矩形,已知PB=PC.?
(1)若P是矩形外一点,求证:PA=PD;?
(2)若P是矩形边AD(或BC)上的一点,则PA PD;
(3)若点P在矩形ABCD内部,上述结论是否仍然成立?
20.在正方形false中,false是false边上一点,
(1)将false绕点false按顺时针方向旋转。使false、false重合,得到false,如图(a)所示.观察可知:与false相等的线段是__________,false__________.
(2)如图(b)所示,正方形false中,false、false分别是false、false边上的点,且false,试通过旋转的方式说明:false.
(3)在(2)的条件下,连接false分别交false、false于点false、false,如图(c)所示.判断false、false、false之间的关系,直接写出结论.
答案
1-5:CBBAC
6-10:BACCD
11.15°
12.false
13.15°
14.②③④
15.false.
16.(1)∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠COD=90°.
∵CE∥OD,DE∥OC,
∴四边形OCED是平行四边形,
又∠COD=90°,
∴平行四边形OCED是矩形;
(2)由(1)知,平行四边形OCED是矩形,则CE=OD=1,DE=OC=2.
∵四边形ABCD是菱形,
∴AC=2OC=4,BD=2OD=2,
∴菱形ABCD的面积为:falseAC?BD=false×4×2=4,
故答案为4.
17.(1)见解析;(2)见解析
【详解】
证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵点E、F分别是AB、CD的中点,
∴BE=falseAB,DF=falseCD.
∴BE=DF,BE∥DF,
∴四边形DFBE是平行四边形,
∴DE∥BF;
(2)∵∠G=90°,AG∥BD,AD∥BG,
∴四边形AGBD是矩形,
∴∠ADB=90°,
在Rt△ADB中
∵E为AB的中点,
∴AE=BE=DE,
∵四边形DFBE是平行四边形,
∴四边形DEBF是菱形.
18.(1)见解收析;(2)当false或false时,四边形false为矩形
【详解】
(1)在false中,
∵false,
∴false.
由题意知,false.
在false与false中,false,
∴false,
∴false,
同理可得false,
∴false,
∴四边形false为平行四边形.
(2)当false或false时,四边形false为矩形.理由如下:
由平行四边形的性质知false,要使false是直角,
只需false,
则false.
∵false,
∴false,
∴false,
即false.
此时false或false.
19.(1)详见解析;(2)=;(3)成立,理由详见解析.
【详解】
(1)证明:如图①,
∵四边形ABCD是矩形,?
∴AB=DC,∠ABC=∠DCB=90°,
∵PB=PC,?
∴∠PBC=∠PCB,
∴∠PBA=∠PCD.
在△APB和△DPC中,false,
∴△APB≌△DPC,
∴PA=PD;
(2) 如图②,当P是矩形边AD上的一点,
∵四边形ABCD是矩形,
∴∠A=∠D=90°,AB=DC,PB=PC,
∴Rt△APB≌Rt△DPC(HL),
∴PA=PD,
当P是矩形边BC上的一点,同理可得:PA=PD,
∴若P是矩形边AD(或BC)上的一点,则PA=PD;
(3)成立.
理由如下:
如图③,
∵四边形ABCD是矩形,?
∴AB=DC,∠ABC=∠DCB=90°,
∵PB=PC,?
∴∠PBC=∠PCB,
∴∠PBA=∠PCD.
在△APB和△DPC中,false,
∴△APB≌△DPC,
∴PA=PD.
20.(1)false,false;(2)见解析;(3)false
【详解】
(1)如图(a).
∵△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF.
∵DE=BF,∠AFB=∠AED.
故答案为:BF,AED;
(2)将△ADQ绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABE,如图2,
则∠D=∠ABE=90°,即点E、B、P共线,∠EAQ=∠BAD=90°,AE=AQ,BE=DQ.
∵∠PAQ=45°,
∴∠PAE=45°,
∴∠PAQ=∠PAE,
在△APE和△APQ中,
∵false,
∴△APE≌△APQ(SAS),
∴PE=PQ,
而PE=PB+BE=PB+DQ,
∴DQ+BP=PQ;
(3)BM2+DN2=MN2.证明如下:
∵四边形ABCD为正方形,
∴∠ABD=∠ADB=45°,
如图3,将△ADN绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABK,
则∠ABK=∠ADN=45°,BK=DN,AK=AN,
与(2)一样可证明△AMN≌△AMK,得到MN=MK.
∵∠MBK=∠MBA+∠KBA=45°+45°=90°,
∴△BMK为直角三角形,
∴BK2+BM2=MK2,
∴BM2+DN2=MN2.
选择题
1.如图,在△ABC中,点D在BC上,DE∥AC,DF∥AB,下列四个判断中不正确的是( )
A.四边形AEDF是平行四边形
B.若∠BAC=90°,则四边形AEDF是矩形
C.若AD平分∠BAC,则四边形AEDF是矩形
D.若AD⊥BC且AB=AC,则四边形AEDF是菱形
2.如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF=( )
A.30° B.45° C.55° D.60°
3.如图,在菱形false中,点false在边false上,false.若false,则边false的长为( )
A.false B.false C.false D.false
4.已知在四边形ABCD中,对角线AC与BD相交于点O,false,下列判断中错误的是( )
A.如果false,false,那么四边形ABCD是平行四边形
B.如果false,false,那么四边形ABCD是矩形
C.如果false,false,那么四边形ABCD是菱形
D.如果false,AC垂直平分BD,那么四边形ABCD是正方形
5.如图,将一张长方形纸片ABCD按图中方式折叠,若AE=3,AB=4,BE=5,则重叠部分的面积为( )
A.6 B.8 C.10 D.12
6.如图,在菱形ABCD中,AB=5,对角线AC与BD相交于点O,且AC:BD=3:4,AE⊥CD于点E,则AE的长是( )
A.4 B.245 C.5 D.125
7.在四边形false中,false,如果再添加一个条件,即可推出该四边形是正方形,这个条件可以是( )
A.false B.false C.false D.false
8.如图所示,矩形ABCD中,AE平分false交BC于E,false,则下面的结论:①false是等边三角形;②false;③false;④false,其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
9.如图,在菱形false中,false,false的垂直平分线交对角线false于点false,false为垂足,连结false,则false等于( )
A.30° B.35° C.40° D.45°
10.如图,菱形false中,过顶点false作false交对角线false于false点,已知false,则false的大小为( )
A.false B.false C.false D.false
二、填空。
11.如图,在正方形ABCD的外侧,作等边△ADE,则∠AEB=_______
12.如图,E为矩形false的边false上一点,将矩形沿false折叠,使点B恰好落在false上的点F处,若false,false,则false_______.
13.如图,长方形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠BAF=60°,则∠DAE等于____________度
14.如图,有下列几组条件:①AC⊥BD,OC=OA;②∠1=∠2=∠3=∠4;③OA=OC,OB=OD,AC⊥BD;④AB=BC=CD,AC⊥BD.其中一定能判定四边形ABCD为菱形的有_________________.(填序号)
15.如图,在菱形false中,false,false的垂直平分线交对角线false于点false,垂足为点false,连接false,false,则false______.
三、解答。
16.如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面积是 .
17.如图,在平行四边形false中,false、false分别为边false、false的中点,false是对角线,过点false作false交false的延长线于点false.
(1)求证:false;
(2)若false,求证:四边形false是菱形.
18.如图,在false中,false,点false在对角线false上,点false从点false出发以每秒1个单位的速度向点false运动,同时点false从点false出发以相同速度向点false运动,到端点时运动停止,运动时间为false秒.
(1)求证;四边形false为平行四边形;
(2)求false为何值时,四边形false为矩形.
19.如图所示,四边形ABCD是矩形,已知PB=PC.?
(1)若P是矩形外一点,求证:PA=PD;?
(2)若P是矩形边AD(或BC)上的一点,则PA PD;
(3)若点P在矩形ABCD内部,上述结论是否仍然成立?
20.在正方形false中,false是false边上一点,
(1)将false绕点false按顺时针方向旋转。使false、false重合,得到false,如图(a)所示.观察可知:与false相等的线段是__________,false__________.
(2)如图(b)所示,正方形false中,false、false分别是false、false边上的点,且false,试通过旋转的方式说明:false.
(3)在(2)的条件下,连接false分别交false、false于点false、false,如图(c)所示.判断false、false、false之间的关系,直接写出结论.
答案
1-5:CBBAC
6-10:BACCD
11.15°
12.false
13.15°
14.②③④
15.false.
16.(1)∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠COD=90°.
∵CE∥OD,DE∥OC,
∴四边形OCED是平行四边形,
又∠COD=90°,
∴平行四边形OCED是矩形;
(2)由(1)知,平行四边形OCED是矩形,则CE=OD=1,DE=OC=2.
∵四边形ABCD是菱形,
∴AC=2OC=4,BD=2OD=2,
∴菱形ABCD的面积为:falseAC?BD=false×4×2=4,
故答案为4.
17.(1)见解析;(2)见解析
【详解】
证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵点E、F分别是AB、CD的中点,
∴BE=falseAB,DF=falseCD.
∴BE=DF,BE∥DF,
∴四边形DFBE是平行四边形,
∴DE∥BF;
(2)∵∠G=90°,AG∥BD,AD∥BG,
∴四边形AGBD是矩形,
∴∠ADB=90°,
在Rt△ADB中
∵E为AB的中点,
∴AE=BE=DE,
∵四边形DFBE是平行四边形,
∴四边形DEBF是菱形.
18.(1)见解收析;(2)当false或false时,四边形false为矩形
【详解】
(1)在false中,
∵false,
∴false.
由题意知,false.
在false与false中,false,
∴false,
∴false,
同理可得false,
∴false,
∴四边形false为平行四边形.
(2)当false或false时,四边形false为矩形.理由如下:
由平行四边形的性质知false,要使false是直角,
只需false,
则false.
∵false,
∴false,
∴false,
即false.
此时false或false.
19.(1)详见解析;(2)=;(3)成立,理由详见解析.
【详解】
(1)证明:如图①,
∵四边形ABCD是矩形,?
∴AB=DC,∠ABC=∠DCB=90°,
∵PB=PC,?
∴∠PBC=∠PCB,
∴∠PBA=∠PCD.
在△APB和△DPC中,false,
∴△APB≌△DPC,
∴PA=PD;
(2) 如图②,当P是矩形边AD上的一点,
∵四边形ABCD是矩形,
∴∠A=∠D=90°,AB=DC,PB=PC,
∴Rt△APB≌Rt△DPC(HL),
∴PA=PD,
当P是矩形边BC上的一点,同理可得:PA=PD,
∴若P是矩形边AD(或BC)上的一点,则PA=PD;
(3)成立.
理由如下:
如图③,
∵四边形ABCD是矩形,?
∴AB=DC,∠ABC=∠DCB=90°,
∵PB=PC,?
∴∠PBC=∠PCB,
∴∠PBA=∠PCD.
在△APB和△DPC中,false,
∴△APB≌△DPC,
∴PA=PD.
20.(1)false,false;(2)见解析;(3)false
【详解】
(1)如图(a).
∵△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF.
∵DE=BF,∠AFB=∠AED.
故答案为:BF,AED;
(2)将△ADQ绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABE,如图2,
则∠D=∠ABE=90°,即点E、B、P共线,∠EAQ=∠BAD=90°,AE=AQ,BE=DQ.
∵∠PAQ=45°,
∴∠PAE=45°,
∴∠PAQ=∠PAE,
在△APE和△APQ中,
∵false,
∴△APE≌△APQ(SAS),
∴PE=PQ,
而PE=PB+BE=PB+DQ,
∴DQ+BP=PQ;
(3)BM2+DN2=MN2.证明如下:
∵四边形ABCD为正方形,
∴∠ABD=∠ADB=45°,
如图3,将△ADN绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABK,
则∠ABK=∠ADN=45°,BK=DN,AK=AN,
与(2)一样可证明△AMN≌△AMK,得到MN=MK.
∵∠MBK=∠MBA+∠KBA=45°+45°=90°,
∴△BMK为直角三角形,
∴BK2+BM2=MK2,
∴BM2+DN2=MN2.
