第十七章勾股定理 章末复习与小结课件(22张)
文档属性
| 名称 | 第十七章勾股定理 章末复习与小结课件(22张) |  | |
| 格式 | pptx | ||
| 文件大小 | 320.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 19:45:37 | ||
图片预览







文档简介
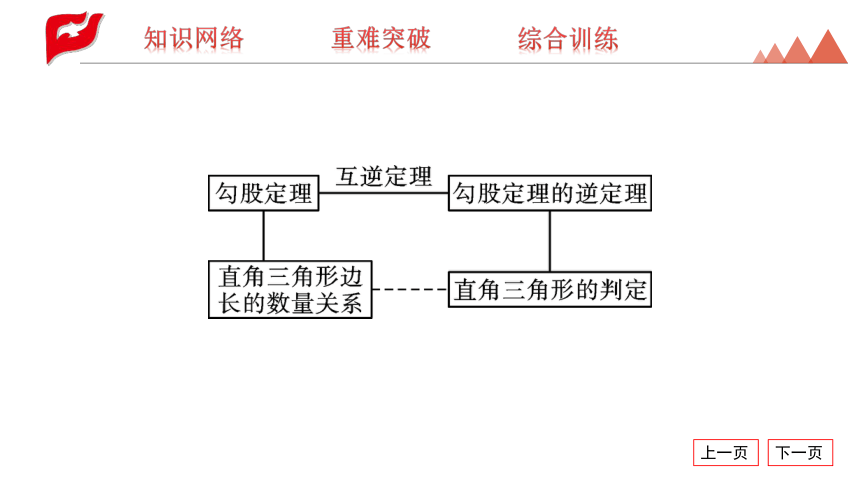
第十七章(勾股定理)
章末复习与小结
八年级数学下册人教版
重热点一 勾股定理
【例1】如图是“赵爽弦图”,△ABH,△BCG,△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH的长为( )
A.2
B.4
C.6
D.8
C
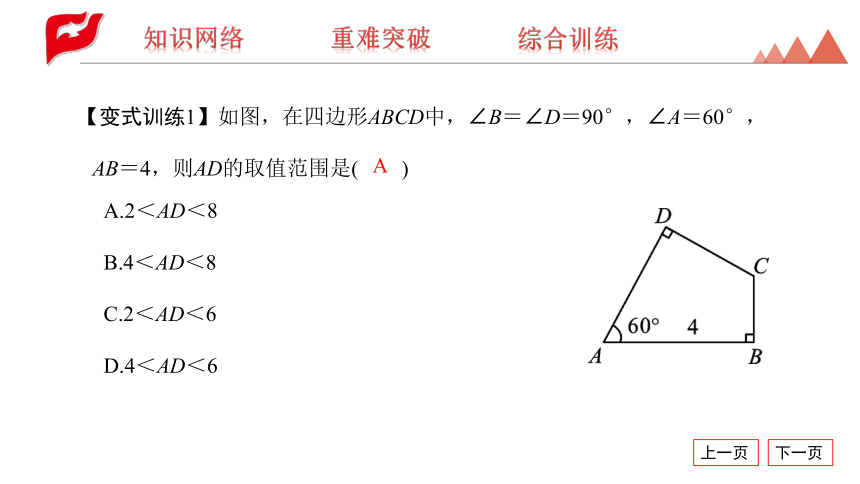
【变式训练1】如图,在四边形ABCD中,∠B=∠D=90°,∠A=60°,AB=4,则AD的取值范围是( )
A.2<AD<8
B.4<AD<8
C.2<AD<6
D.4<AD<6
A
【变式训练2】在△ABC中,∠C=90°,AC=8 cm,BC=6 cm.动点P从点C开始,按C→A→B→C的路径运动,速度为每秒2 cm,运动的时间为t秒.以下结论:①当t为6秒时,CP把△ABC的周长分成相等的两部分;②当t为6.5秒时,CP把△ABC分成面积相等的两部分;③当t为3秒或5.4秒或6秒或6.5秒时,△BCP为等腰三角形.其中正确的有( )
A.①②③ B.①② C.②③ D.①③
A
重热点二 勾股定理的逆定理
【例2】(9分)如图,在5×5的方格纸中,每一个小正方形的边长都为1,四边形ABCD的顶点都在格点上.
(1)∠BCD是不是直角?请说明理由;
解:(1)∠BCD是直角.……………………………………………………(1分)
理由如下:连接BD.
∵BC2=22+42=20,CD2=12+22=5,BD2=32+42=25,…………(4分)
∴BD2=BC2+CD2,∴∠BCD是直角. …………………………………(6分)
(2)求四边形ABCD的面积.(可以根据需要添加字母)
(2)根据图示知,S四边形ABCD=S正方形AHEJ-S△BCE-S△ABH-S△ADI-S△DCF-S正方形DFJI,………………………………………(7分)
则S四边形ABCD= 5×5- ×2×4- ×1×5- ×1×4-
×2×1-1×1=14.5,即四边形ABCD的面积是14.5. ………………………………………………………………(9分)
评分说明:
1.正确判断∠BCD是直角,得1分;
2.正确计算三条线段的长度的平方得3分;
3.正确利用勾股定理的逆定理,得到∠BCD是直角得2分;
4.正确分割四边形的面积,得1分;
5.正确计算四边形面积得2分.
重热点三 勾股定理的应用
【例3】如图,∠AOB=90°,OA=9 cm,OB=3 cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿BC方向匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,则机器人行走的路程BC长为________.
5 cm
一、选择题
1.分别以下列四组数作为三角形的三边长:①3,4,5;②5,12,13;③8,15,17;④32,42,52.其中能构成直角三角形的有( )
A.4组 B.3组 C.2组 D.1组
B
2.如图,在△ABC中,∠C=90°,CB=8 cm,AC=6 cm,则点C到AB的距离是( )
A.4.8 cm
B.6 cm
C.8 cm
D. cm
A
3.一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,∠B=90°,AB=8米,BC=6米.当DC2=AE2+BC2时,AE的长为( )
A.2米
B.2.5米
C.3.4米
D.3.6米
C
4.在古代《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”译文:“有一架秋千,当它静止时,踏板离地1尺,将它往前推送10尺(水平距离)时,秋千的踏板就和人一样高,这个人的身高为5尺,秋千的绳索始终拉得很直,试问绳索有多长?”则绳索的长为( )
A.12.5尺
B.13.5尺
C.14.5尺
D.15.5尺
C
二、填空题
5.将一根长为x cm的细木棒放进一个内部长、宽、高分别是50 cm,40 cm,30 cm的木箱中,则x的最大值为________.
6.如图,某自动感应门的正上方装着一个感应器,离地2.5米,当物体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.6米的学生正对门,缓慢走到离门1.2米的地方时,感应门才自动打开,则感应器的最大感应距离是________米.
1.5
7.在△ABC中,如果AB=5 cm,AC=4 cm,BC边上的高线AD=3 cm,那么BC的长为_____________________cm.
三、解答题
8.如图,在平面直角坐标系中,四边形OABC为长方形,点A的坐标为(10,0),点C的坐标为(0,6),将边BC折叠,使点B落在边OA上的点D处,求线段EA的长.
解:∵点A的坐标为(10,0),点C的坐标为(0,6),
∴OA=10,OC=6.
由题意,得AB=OC=6,CD=BC=AO=10,
∠EAD=∠COD=90°,DE=BE.
在Rt△COD中,根据勾股定理,得
∴DA=OA-OD=2,设EA=x,则BE=ED=6-x.
在Rt△EAD中,根据勾股定理,得EA2+AD2=ED2,
∴x2+22=(6-x)2,解得 ,∴EA的长为
9.在一条东西走向的河的一侧有一村庄C,河边原有两个取水点A,B,且AB=AC.由于某种原因,由C到A的路现在已经不通,为方便村民取水,该村庄决定在河边新建一个取水点H(点A,H,B在一条直线上),并新修一条路CH,测得BC=3 km,CH=2.4 km,BH=1.8 km.
(1)问CH是否为从村庄C到河边的最近路线?请通过计算加以说明;
解:是.理由如下:在△CHB中,
∵CH2+BH2=2.42+1.82=9,BC2=9,
∴CH2+BH2=BC2,
∴△CHB是直角三角形,且∠CHB=90°,
∴CH⊥AB,∴CH是从村庄C到河边的最近路线.
(2)求原来的路线AC的长.
解:设AC=x km,则AB=x km,
AH=AB-BH=(x-1.8)km.
在Rt△ACH中,由勾股定理,得AC2=AH2+CH2,
即x2=(x-1.8)2+2.42,解得x=2.5.
答:原来的路线AC的长为2.5 km.
章末复习与小结
八年级数学下册人教版
重热点一 勾股定理
【例1】如图是“赵爽弦图”,△ABH,△BCG,△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH的长为( )
A.2
B.4
C.6
D.8
C
【变式训练1】如图,在四边形ABCD中,∠B=∠D=90°,∠A=60°,AB=4,则AD的取值范围是( )
A.2<AD<8
B.4<AD<8
C.2<AD<6
D.4<AD<6
A
【变式训练2】在△ABC中,∠C=90°,AC=8 cm,BC=6 cm.动点P从点C开始,按C→A→B→C的路径运动,速度为每秒2 cm,运动的时间为t秒.以下结论:①当t为6秒时,CP把△ABC的周长分成相等的两部分;②当t为6.5秒时,CP把△ABC分成面积相等的两部分;③当t为3秒或5.4秒或6秒或6.5秒时,△BCP为等腰三角形.其中正确的有( )
A.①②③ B.①② C.②③ D.①③
A
重热点二 勾股定理的逆定理
【例2】(9分)如图,在5×5的方格纸中,每一个小正方形的边长都为1,四边形ABCD的顶点都在格点上.
(1)∠BCD是不是直角?请说明理由;
解:(1)∠BCD是直角.……………………………………………………(1分)
理由如下:连接BD.
∵BC2=22+42=20,CD2=12+22=5,BD2=32+42=25,…………(4分)
∴BD2=BC2+CD2,∴∠BCD是直角. …………………………………(6分)
(2)求四边形ABCD的面积.(可以根据需要添加字母)
(2)根据图示知,S四边形ABCD=S正方形AHEJ-S△BCE-S△ABH-S△ADI-S△DCF-S正方形DFJI,………………………………………(7分)
则S四边形ABCD= 5×5- ×2×4- ×1×5- ×1×4-
×2×1-1×1=14.5,即四边形ABCD的面积是14.5. ………………………………………………………………(9分)
评分说明:
1.正确判断∠BCD是直角,得1分;
2.正确计算三条线段的长度的平方得3分;
3.正确利用勾股定理的逆定理,得到∠BCD是直角得2分;
4.正确分割四边形的面积,得1分;
5.正确计算四边形面积得2分.
重热点三 勾股定理的应用
【例3】如图,∠AOB=90°,OA=9 cm,OB=3 cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿BC方向匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,则机器人行走的路程BC长为________.
5 cm
一、选择题
1.分别以下列四组数作为三角形的三边长:①3,4,5;②5,12,13;③8,15,17;④32,42,52.其中能构成直角三角形的有( )
A.4组 B.3组 C.2组 D.1组
B
2.如图,在△ABC中,∠C=90°,CB=8 cm,AC=6 cm,则点C到AB的距离是( )
A.4.8 cm
B.6 cm
C.8 cm
D. cm
A
3.一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,∠B=90°,AB=8米,BC=6米.当DC2=AE2+BC2时,AE的长为( )
A.2米
B.2.5米
C.3.4米
D.3.6米
C
4.在古代《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”译文:“有一架秋千,当它静止时,踏板离地1尺,将它往前推送10尺(水平距离)时,秋千的踏板就和人一样高,这个人的身高为5尺,秋千的绳索始终拉得很直,试问绳索有多长?”则绳索的长为( )
A.12.5尺
B.13.5尺
C.14.5尺
D.15.5尺
C
二、填空题
5.将一根长为x cm的细木棒放进一个内部长、宽、高分别是50 cm,40 cm,30 cm的木箱中,则x的最大值为________.
6.如图,某自动感应门的正上方装着一个感应器,离地2.5米,当物体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.6米的学生正对门,缓慢走到离门1.2米的地方时,感应门才自动打开,则感应器的最大感应距离是________米.
1.5
7.在△ABC中,如果AB=5 cm,AC=4 cm,BC边上的高线AD=3 cm,那么BC的长为_____________________cm.
三、解答题
8.如图,在平面直角坐标系中,四边形OABC为长方形,点A的坐标为(10,0),点C的坐标为(0,6),将边BC折叠,使点B落在边OA上的点D处,求线段EA的长.
解:∵点A的坐标为(10,0),点C的坐标为(0,6),
∴OA=10,OC=6.
由题意,得AB=OC=6,CD=BC=AO=10,
∠EAD=∠COD=90°,DE=BE.
在Rt△COD中,根据勾股定理,得
∴DA=OA-OD=2,设EA=x,则BE=ED=6-x.
在Rt△EAD中,根据勾股定理,得EA2+AD2=ED2,
∴x2+22=(6-x)2,解得 ,∴EA的长为
9.在一条东西走向的河的一侧有一村庄C,河边原有两个取水点A,B,且AB=AC.由于某种原因,由C到A的路现在已经不通,为方便村民取水,该村庄决定在河边新建一个取水点H(点A,H,B在一条直线上),并新修一条路CH,测得BC=3 km,CH=2.4 km,BH=1.8 km.
(1)问CH是否为从村庄C到河边的最近路线?请通过计算加以说明;
解:是.理由如下:在△CHB中,
∵CH2+BH2=2.42+1.82=9,BC2=9,
∴CH2+BH2=BC2,
∴△CHB是直角三角形,且∠CHB=90°,
∴CH⊥AB,∴CH是从村庄C到河边的最近路线.
(2)求原来的路线AC的长.
解:设AC=x km,则AB=x km,
AH=AB-BH=(x-1.8)km.
在Rt△ACH中,由勾股定理,得AC2=AH2+CH2,
即x2=(x-1.8)2+2.42,解得x=2.5.
答:原来的路线AC的长为2.5 km.
