2.4.2 一元一次不等式应用 课件(共19张PPT)
文档属性
| 名称 | 2.4.2 一元一次不等式应用 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 00:00:00 | ||
图片预览






文档简介
2.4.2 一元一次不等式应用
第二章 一元一次不等式和一元一次不等式组
2020-2021北师大版七年级数学下册
1.会通过列一元一次不等式去解决生活中的实际问题,经历 “实际问题抽象为不等式模型”的过程;
2.体会解不等式过程中的化归思想与类比思想,体会分类讨论思想在用不等式解决实际问题中的应用.
学习目标
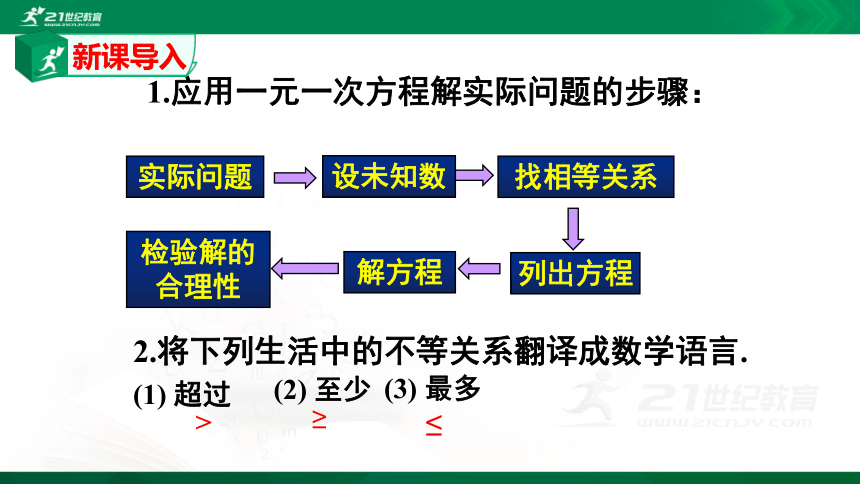
1.应用一元一次方程解实际问题的步骤:
实际问题
找相等关系
设未知数
列出方程
检验解的合理性
解方程
2.将下列生活中的不等关系翻译成数学语言.
(1) 超过
(2) 至少
(3) 最多
>
≥
≤
新课导入
一元一次不等式的应用
1.某种商品进价为200元,标价300元出售,商场规定可以打折销售,但其利润率不能少于5%.请你帮助售货员计算一下,这种商品最多可以按几折销售?
解得x≥7.
答:这种商品最多可以按7折销售.
解:设这种商品可以按x折销售,由题意得
不等关系:利润率=(售价-进价)/进价≥5%
利润=售价-进价≥利润率×进价
探究新知
经济问题的概念:
(1)成本价(进价);
(2)标价(定价);
(3)售价(打折价、成交价);
(4)利润=售价-成本价
(5)利润率=利润/成本价
=(售价-成本价)/成本价
打折—乘 x/10
利润=成本价×利润率
解:设小明答对了x道题,则答错或不答的共有
(25-x)道题,根据题意,得
4x-1×(25-x) ≥85
解得 x≥22
答:小明至少答对了22道题,由于共有25道题,因此他可能答对22,23,24或25道题。
2.一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分,在这次竞赛中小明被评为优秀(85分或85分以上),小明至少答对了几道题?
不等关系:答对的分数-答错或不答的分数≥ 85
一元一次不等式的应用
应用一元一次不等式解决实际问题的步骤:
实际问题
解不等式
列不等式
结合实际
确定答案
找出不等关系
设未知数
总结归纳
1.某种商品进价为400元,出售时标价500元,商场准备打折销售,但要保持利润不低于10%.则至多可打几折?
解:设此商品可以按x折销售,由题意得
解得:x ≥8.8
答:设此商品可以按8.8折销售
课堂练习
2.小明准备用26元钱买火腿肠和方便面,已知一根火腿肠2元钱,一盒方便面3元钱,他买了5盒方便面,他还可能买多少根火腿肠?
解:设小明买了x根火腿肠,根据题意得:
2x+3×5 ≤26
解得 x ≤5.5
∵x只能取正整数
∴x可以取1、2、3、4、5
答:他还可能买了1、2、3、4、5根火腿肠。
3.为了举办班级晚会,孔明准备去商店购买20个乒乓球做道具,并买一些乒乓球拍做奖品,已知乒乓球每个1.5元,球拍每个22元,如果购买金额不能超过200元,且买的球拍要尽可能多,那么孔明应该买多少个球拍?
解:设购买球拍x个,依题意得:
1.5×20+22x≤200,
解得x ≤7 ,
∵ x取整数, ∴ x的最大值为7.
答:孔明应该买7个球拍.
4.小兰准备用30元买钢笔和笔记本,已知一支钢笔4.5元,一本笔记本3元.
(1)她买了5本笔记本,则她最多还可以买多少支钢笔?
钢笔费用+笔记本的费用≤30
解:设她还可以买x支钢笔,由题意,得
4.5x+3×5≤30
∵X为整数,∴X=3
答:最多还可以买3支钢笔
4.小兰准备用30元买钢笔和笔记本,已知一支钢笔4.5元,一本笔记本3元。(2)如果她钢笔和笔记本共买了8件,则她最多可以买多少支钢笔?则她有多少种购买方案?
解:设她可以买x支钢笔,则笔记本为(8-x)个,得
4.5x+3(8-x)≤30
解得:x≤4
答:她最多可以买4支钢笔,有5种买法。
∵x为整数,∴x可取0、1、2、3、4
5.我班几个同学合影留念,每人交0.7元,已知一张彩色底片0.68元,打印一张相片0.5元,每人分一张,在将收来的钱尽量用掉的前提下,这张相片上的同学最少有几人?
解:设这张相片上的同学有x人,根据题意,得
0.7x≥0.68+0.5x
x≥3.4
∵X为整数,∴X=4
答:这张相片上的同学最少有4人。
6. 当一个人坐下时,不宜提举超过4.5 kg的重物,以免受伤. 小明坐在书桌前,桌上有两本各重1.2 kg的画册和一批每本重0.4 kg的记事本. 如果小明想坐着搬动这两本画册和一些记事本. 问他最多只应搬动多少本记事本?
解: 设小明最多只应搬动x本记事本,则
解得 x≤5.25.
1.2×2+0.4x≤4.5.
答:小明最多只应搬动5本记事本.
由于记事本的数目必须是整数,所以x 的最大值为5.
分析: 本题涉及的数量关系是:
画册的总重+记事本的总重≤4.5 kg.
7.小明家的客厅长5 m,宽4 m.现在想购买边长为60 cm的正方形地板砖把地面铺满,至少需要购买多少块这样的地板砖?
解: 设需要购买x块地板砖,则有
5×4≤0.6×0.6x
解得 x ≥ 55.6
由于地板砖的数目必须是整数,所以x的最
小值为56.
答:小明至少要购买56块地板砖.
8. 某童装店按每套90元的价格购进40套童装,应缴纳的税费为销售额的10%. 如果要获得不低于900元的纯利润,每套童装的售价至少是多少元?
解: 设每套童装的售价是 x 元.
则 40x-90×40-40x·10%≥900.
解得
x ≥ 125.
答:每套童装的售价至少是125元.
分析: 本题涉及的数量关系是:
销售额-成本-税费≥纯利润(900元).
一元一次不等式的应用
实际问题
↓
根据题意列不等式
↓
解一元一次不等式
→
→
根据实际问题找出符合条件的解集或整数解
↑
得出解决问题的答案
课堂小结
谢谢聆听
第二章 一元一次不等式和一元一次不等式组
2020-2021北师大版七年级数学下册
1.会通过列一元一次不等式去解决生活中的实际问题,经历 “实际问题抽象为不等式模型”的过程;
2.体会解不等式过程中的化归思想与类比思想,体会分类讨论思想在用不等式解决实际问题中的应用.
学习目标
1.应用一元一次方程解实际问题的步骤:
实际问题
找相等关系
设未知数
列出方程
检验解的合理性
解方程
2.将下列生活中的不等关系翻译成数学语言.
(1) 超过
(2) 至少
(3) 最多
>
≥
≤
新课导入
一元一次不等式的应用
1.某种商品进价为200元,标价300元出售,商场规定可以打折销售,但其利润率不能少于5%.请你帮助售货员计算一下,这种商品最多可以按几折销售?
解得x≥7.
答:这种商品最多可以按7折销售.
解:设这种商品可以按x折销售,由题意得
不等关系:利润率=(售价-进价)/进价≥5%
利润=售价-进价≥利润率×进价
探究新知
经济问题的概念:
(1)成本价(进价);
(2)标价(定价);
(3)售价(打折价、成交价);
(4)利润=售价-成本价
(5)利润率=利润/成本价
=(售价-成本价)/成本价
打折—乘 x/10
利润=成本价×利润率
解:设小明答对了x道题,则答错或不答的共有
(25-x)道题,根据题意,得
4x-1×(25-x) ≥85
解得 x≥22
答:小明至少答对了22道题,由于共有25道题,因此他可能答对22,23,24或25道题。
2.一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分,在这次竞赛中小明被评为优秀(85分或85分以上),小明至少答对了几道题?
不等关系:答对的分数-答错或不答的分数≥ 85
一元一次不等式的应用
应用一元一次不等式解决实际问题的步骤:
实际问题
解不等式
列不等式
结合实际
确定答案
找出不等关系
设未知数
总结归纳
1.某种商品进价为400元,出售时标价500元,商场准备打折销售,但要保持利润不低于10%.则至多可打几折?
解:设此商品可以按x折销售,由题意得
解得:x ≥8.8
答:设此商品可以按8.8折销售
课堂练习
2.小明准备用26元钱买火腿肠和方便面,已知一根火腿肠2元钱,一盒方便面3元钱,他买了5盒方便面,他还可能买多少根火腿肠?
解:设小明买了x根火腿肠,根据题意得:
2x+3×5 ≤26
解得 x ≤5.5
∵x只能取正整数
∴x可以取1、2、3、4、5
答:他还可能买了1、2、3、4、5根火腿肠。
3.为了举办班级晚会,孔明准备去商店购买20个乒乓球做道具,并买一些乒乓球拍做奖品,已知乒乓球每个1.5元,球拍每个22元,如果购买金额不能超过200元,且买的球拍要尽可能多,那么孔明应该买多少个球拍?
解:设购买球拍x个,依题意得:
1.5×20+22x≤200,
解得x ≤7 ,
∵ x取整数, ∴ x的最大值为7.
答:孔明应该买7个球拍.
4.小兰准备用30元买钢笔和笔记本,已知一支钢笔4.5元,一本笔记本3元.
(1)她买了5本笔记本,则她最多还可以买多少支钢笔?
钢笔费用+笔记本的费用≤30
解:设她还可以买x支钢笔,由题意,得
4.5x+3×5≤30
∵X为整数,∴X=3
答:最多还可以买3支钢笔
4.小兰准备用30元买钢笔和笔记本,已知一支钢笔4.5元,一本笔记本3元。(2)如果她钢笔和笔记本共买了8件,则她最多可以买多少支钢笔?则她有多少种购买方案?
解:设她可以买x支钢笔,则笔记本为(8-x)个,得
4.5x+3(8-x)≤30
解得:x≤4
答:她最多可以买4支钢笔,有5种买法。
∵x为整数,∴x可取0、1、2、3、4
5.我班几个同学合影留念,每人交0.7元,已知一张彩色底片0.68元,打印一张相片0.5元,每人分一张,在将收来的钱尽量用掉的前提下,这张相片上的同学最少有几人?
解:设这张相片上的同学有x人,根据题意,得
0.7x≥0.68+0.5x
x≥3.4
∵X为整数,∴X=4
答:这张相片上的同学最少有4人。
6. 当一个人坐下时,不宜提举超过4.5 kg的重物,以免受伤. 小明坐在书桌前,桌上有两本各重1.2 kg的画册和一批每本重0.4 kg的记事本. 如果小明想坐着搬动这两本画册和一些记事本. 问他最多只应搬动多少本记事本?
解: 设小明最多只应搬动x本记事本,则
解得 x≤5.25.
1.2×2+0.4x≤4.5.
答:小明最多只应搬动5本记事本.
由于记事本的数目必须是整数,所以x 的最大值为5.
分析: 本题涉及的数量关系是:
画册的总重+记事本的总重≤4.5 kg.
7.小明家的客厅长5 m,宽4 m.现在想购买边长为60 cm的正方形地板砖把地面铺满,至少需要购买多少块这样的地板砖?
解: 设需要购买x块地板砖,则有
5×4≤0.6×0.6x
解得 x ≥ 55.6
由于地板砖的数目必须是整数,所以x的最
小值为56.
答:小明至少要购买56块地板砖.
8. 某童装店按每套90元的价格购进40套童装,应缴纳的税费为销售额的10%. 如果要获得不低于900元的纯利润,每套童装的售价至少是多少元?
解: 设每套童装的售价是 x 元.
则 40x-90×40-40x·10%≥900.
解得
x ≥ 125.
答:每套童装的售价至少是125元.
分析: 本题涉及的数量关系是:
销售额-成本-税费≥纯利润(900元).
一元一次不等式的应用
实际问题
↓
根据题意列不等式
↓
解一元一次不等式
→
→
根据实际问题找出符合条件的解集或整数解
↑
得出解决问题的答案
课堂小结
谢谢聆听
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
