18.2.2 菱形课件(26张)
图片预览


文档简介
1.经历类比矩形判定探索菱形判定方法的过程,会推理论证。
2.掌握菱形判定定理,会灵活应用,体会转化的数学思想。
3.培养主动探究、观察归纳、几何说理能力。
平行四边形
菱形
一组邻边相等
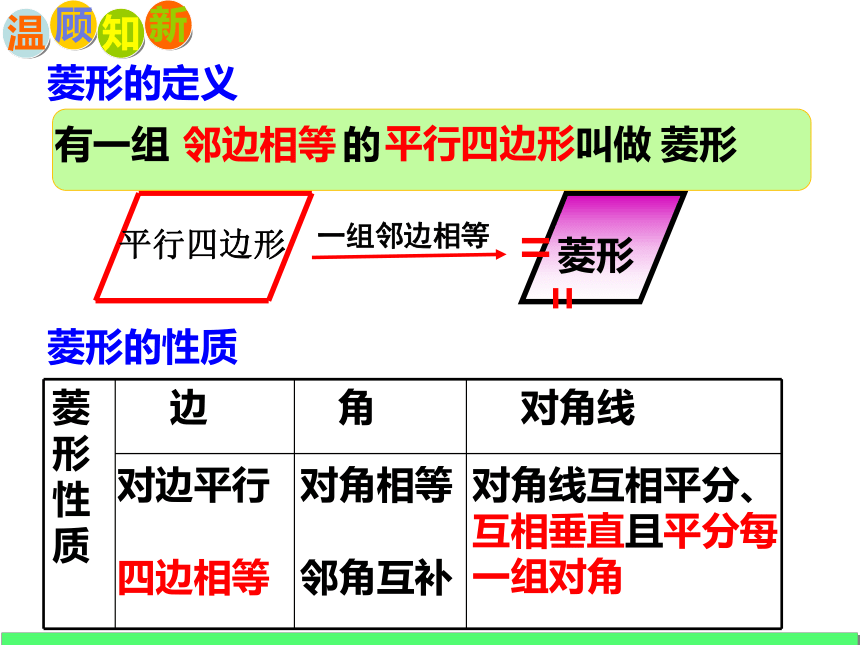
菱形的定义
有一组 的 叫做
邻边相等
平行四边形
菱形
菱形的性质
菱形性质
边
角
对角线
对边平行
对角相等
对角线互相平分、互相垂直且平分每一组对角
邻角互补
四边相等
温
顾
知
新
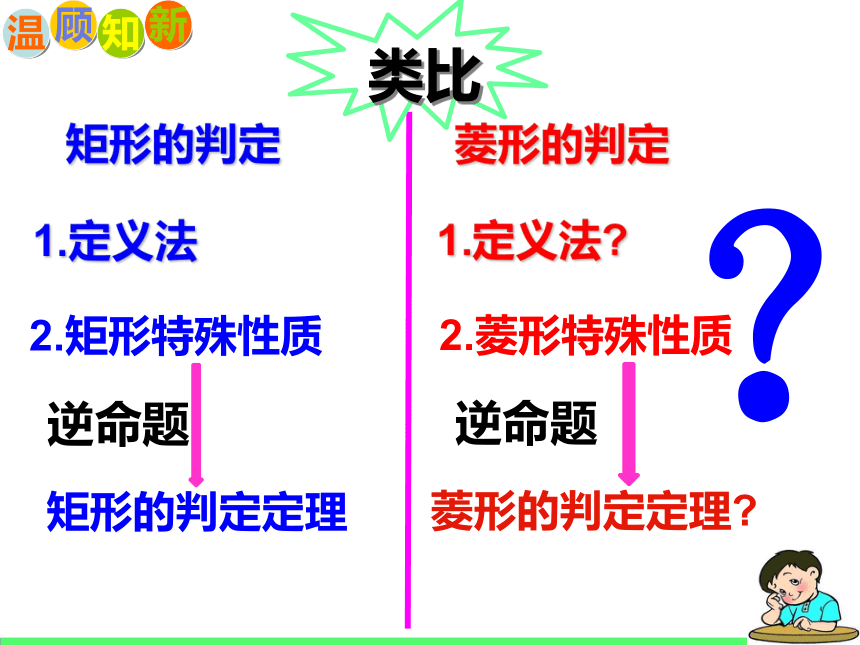
类比
矩形的判定
1.定义法
2.矩形特殊性质
矩形的判定定理
逆命题
菱形的判定
1.定义法?
2.菱形特殊性质
逆命题
菱形的判定定理?
?
温
顾
知
新
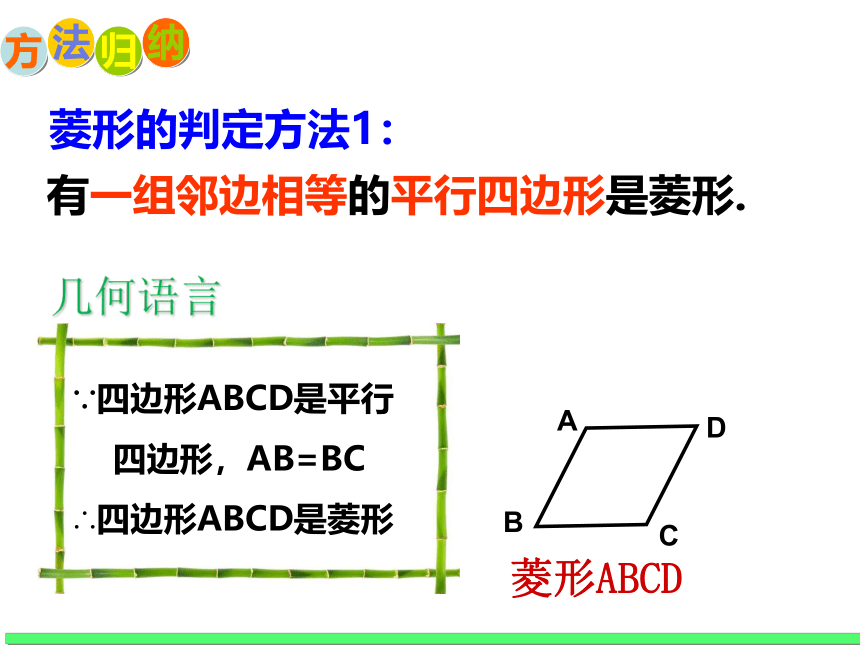
几何语言
∵四边形ABCD是平行
四边形,AB=BC
∴四边形ABCD是菱形
A
B
C
D
菱形ABCD
方
法
归
纳
有一组邻边相等的平行四边形是菱形.
菱形的判定方法1:
探
究
新
知
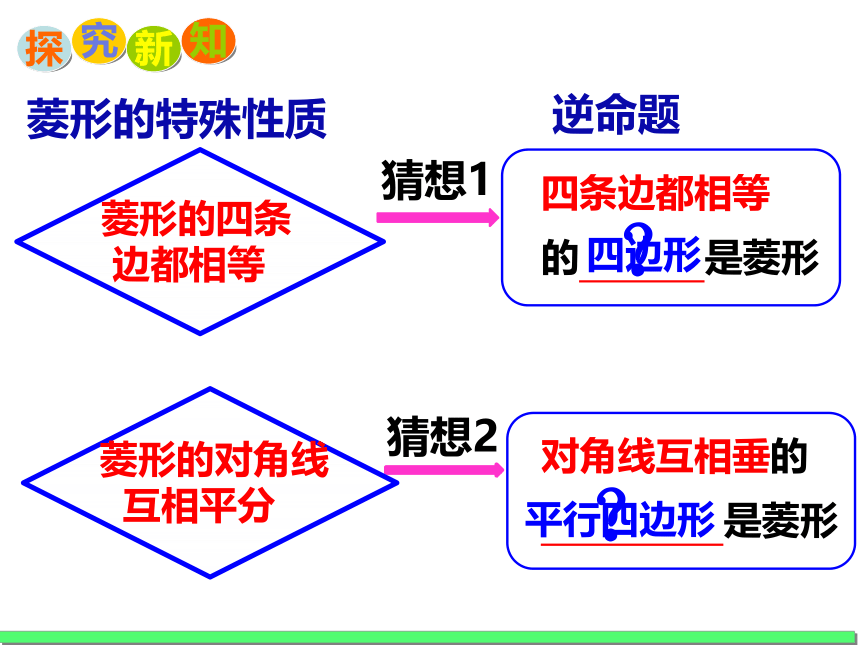
菱形的特殊性质
逆命题
四条边都相等
的 是菱形
菱形的四条
边都相等
?
对角线互相垂的
是菱形
菱形的对角线
互相平分
?
猜想1
猜想2
四边形
平行四边形
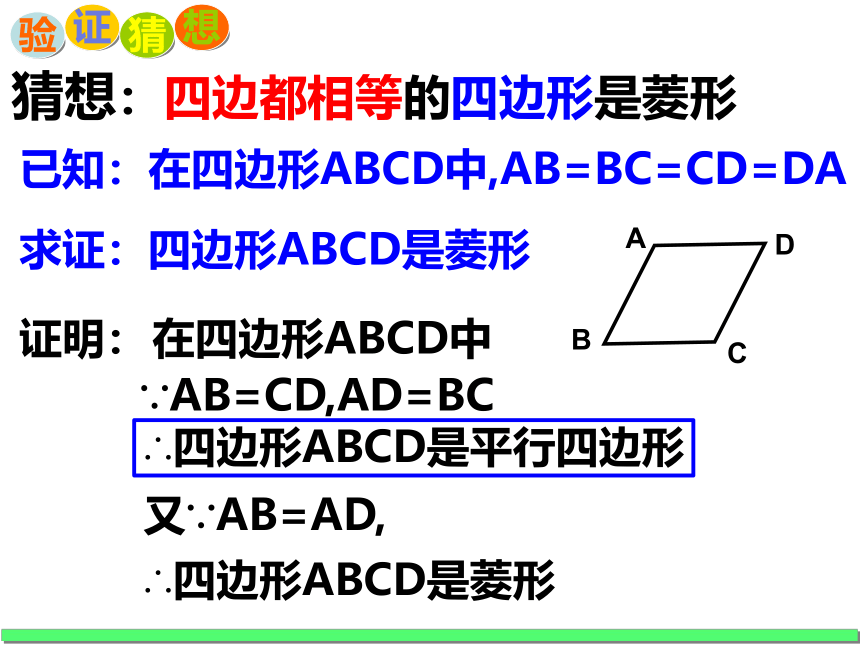
已知:在四边形ABCD中,AB=BC=CD=DA
证明:
在四边形ABCD中
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=AD,
∴四边形ABCD是菱形
A
B
C
D
猜想:四边都相等的四边形是菱形
求证:四边形ABCD是菱形
验
证
猜
想
几何语言
方
法
归
纳
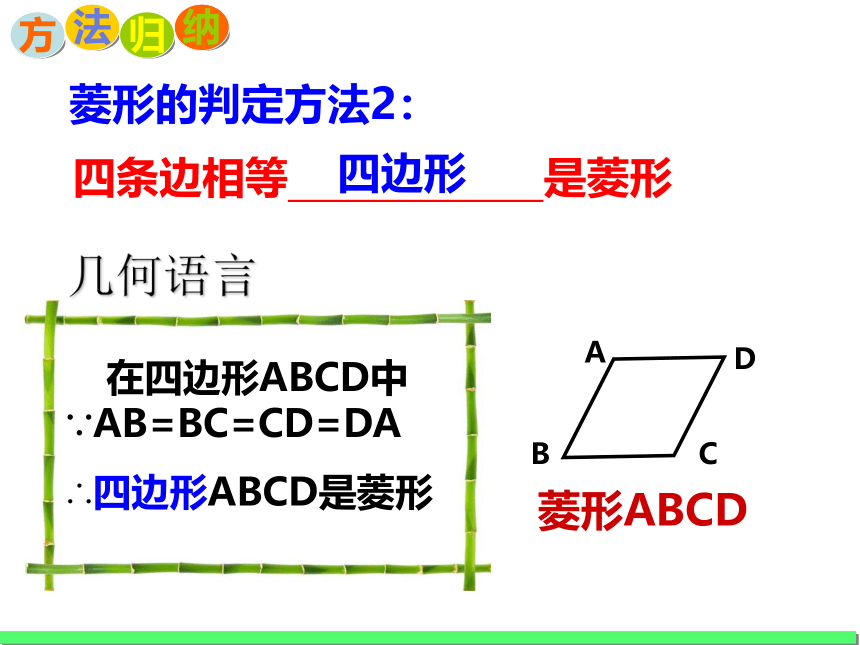
在四边形ABCD中∵AB=BC=CD=DA
∴四边形ABCD是菱形
A
B
C
D
菱形ABCD
菱形的判定方法2:
四边形
四条边相等 是菱形
验
证
猜
想
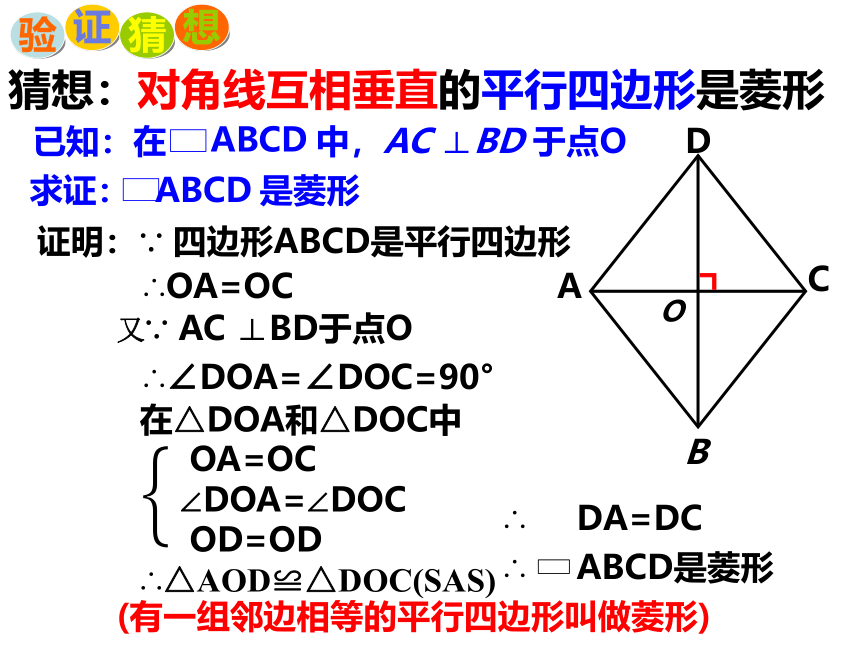
猜想:对角线互相垂直的平行四边形是菱形
已知:在 中,AC ⊥BD 于点O
ABCD
求证: 是菱形
ABCD
证明:
∵ 四边形ABCD是平行四边形
又∵ AC ⊥BD于点O
∴OA=OC
∴∠DOA=∠DOC=90°
OA=OC
∠DOA=∠DOC
OD=OD
∴△AOD≌△DOC(SAS)
在△DOA和△DOC中
∴ DA=DC
D
C
B
A
O
┓
∴ ABCD是菱形
{
(有一组邻边相等的平行四边形叫做菱形)
验
证
猜
想
猜想:对角线互相垂直的平行四边形是菱形
已知:在 中,AC ⊥BD 于点O
ABCD
求证: 是菱形
ABCD
证明:
∵ 四边形ABCD是平行四边形
又∵ AC ⊥BD于点O
∴ OA=OC
∴ DA=DC
D
C
B
A
O
┓
∴ ABCD是菱形
(线段垂直平分线上的点,到线段两个端点的距离相等)
(有一组邻边相等的平行四边形叫做菱形)
几何语言
方
法
归
纳
∵ 四边形ABCD是平行四边形
又∵AC⊥BD于点O;
∴□ ABCD是菱形
菱形的判定方法3:
对角线互相垂直的 是菱形
平行四边形
A
B
C
D
菱形ABCD
O
方
法
归
纳
①有一组邻边相等
②对角线互相垂直
四条边相等的四边形是菱形
判定菱形时,要注意是从“四边形”出发,还是从“平行四边形”出发这个前提条件
明
辨
是
非
1.有一组邻边相等的四边形是菱形。
2.对角线互相平分且邻边相等的四边形是菱形。
3.有三边相等的四边形是菱形。
4.对角线互相垂直的四边形是菱形。
5.对角线互相垂直且平分的四边形是菱形。
判断下列命题是否正确,错误的请改正.
①先判定平行四边形;
②再寻找一个条件.
活
学
活
用
如图,在四边形ABCD中,已知AB∥ CD,
AB=CD,在不添加任何辅助线的前提下,请你添加一个适当的条件,使四边形ABCD是菱形 : (只需添加一个即可)
A
B
C
D
O
体验之旅----努力造就实力
探索之旅----态度决定高度
智慧之旅----善用内在潜能
闯关之旅----拼搏成就梦想
四条边都相等
菱形
一组邻边相等
对角线互相垂直
对角线互相平分
一组对边平行且相等
二组对边平行或相等
四边形
平行四边形
两组对角相等
善于总结是学习的前提条件
我的收获----
数学课上,老师让同学们判断一个四边形是否为菱形,下面是某合作小组4名同学拟定的方案,其中正确的是 ( )
A.测量对角线是否相等
B.测量对角线是否垂直
C.测量一组对角是否相等
D.测量四边是否相等
D
(四条边都相等的四边形是菱形)
体验之旅----努力造就实力
如图, ABCD 的对角线AC、BD相交于点O,
且AO=3,BO=4,AB=5.
求证: ABCD是菱形.
A
B
C
D
O
证明:∵ AO=3,BO=4,AB=5
∴AB2=AO2+BO2
∴△OAB是直角三角形
∴AC⊥BD于点O
又∵四边形ABCD是平行四边形
∴四边形ABCD是菱形
(对角线互相垂直的平行四边形是菱形)
探索之旅----态度决定高度
∴AO2+BO2=32+42=25,AB2=25
已知:如图,AD平分∠BAC,DE∥AC 交AB
于E,DF∥AB交AC于F.
求证:四边形AEDF是菱形.
∴ □AEDF是菱形
∵DE∥AC DF∥AB
∴四边形AEDF是平行四边形
∵ DE∥AC∴∠2=∠3
∵ AD平分∠BAC∴ ∠1=∠2
∴AE=DE
∴ ∠1=∠3
证明:
(一组邻边相等的平行四边形是菱形)
A
B
C
F
D
E
1
2
3
智慧之旅----善用内在潜能
(2018.新疆中考)
如图,在矩形ABCD中,点P是线段AD上的一个动点,O是BD的中点,PO的延长线交BC于点Q。
(1)求证:四边形PBQD是平行四边形;
(2)若AD=6cm,AB=4cm,P从A出发以1cm/s的速度向D运动(不于D重合),设点P运动的时间为t秒。
①请用t表示PD的长;
②当t为何值时,四边形
PBQD是菱形。
C
B
D
P
O
A
Q
闯关之旅----拼搏成就梦想
四条边都相等
菱形
一组邻边相等
对角线互相垂直
对角线互相平分
一组对边平行且相等
二组对边平行或相等
四边形
平行四边形
两组对角相等
善于总结是学习的前提条件
我的收获----
菱形的判定
已知平行四边形,邻边相等叫菱形;
两对角线若垂直,顺理成章成菱形 。
任意一个四边形,四边相等叫菱形;
四边形的对角线,垂直平分是菱形 。
我
有
绝
招
1.大练习册一个课时
2.导学案--课后练习 ①必做 ②选做
分
层
作
业
如图,两张等宽的纸条交叉重叠在一起,重叠的部分ABCD是菱形吗?求证:
(1)四边形ABCD是平行四边形
(2)过A作AE⊥BC于E点, 过A作AF⊥CD 于F.用等积法说明BC=CD.
(3)求证:四边形ABCD是菱形.
A
C
D
B
奇妙之旅----
D
C
B
A
解:过点A作AE⊥BC于点E,AF⊥CD于点F
∵ 两纸条的宽度相同
∴ AE=AF
由题意可知:AB∥CD, AD∥BC
∴ 四边形ABCD是平行四边形
∵ S ABCD=BC ? AE=CD? AF
又 ∵ AE=AF
∴ BC=CD
∴ 四边形ABCD是菱形
如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形。
H
G
F
E
D
C
B
A
证明:连接AC、BD
∵四边形ABCD是矩形
∴AC=BD
∵点E、F、G、H为各边中点
∴EF=FG=GH=HE
∴四边形EFGH是菱形
收获之旅----
中点四边形
2.掌握菱形判定定理,会灵活应用,体会转化的数学思想。
3.培养主动探究、观察归纳、几何说理能力。
平行四边形
菱形
一组邻边相等
菱形的定义
有一组 的 叫做
邻边相等
平行四边形
菱形
菱形的性质
菱形性质
边
角
对角线
对边平行
对角相等
对角线互相平分、互相垂直且平分每一组对角
邻角互补
四边相等
温
顾
知
新
类比
矩形的判定
1.定义法
2.矩形特殊性质
矩形的判定定理
逆命题
菱形的判定
1.定义法?
2.菱形特殊性质
逆命题
菱形的判定定理?
?
温
顾
知
新
几何语言
∵四边形ABCD是平行
四边形,AB=BC
∴四边形ABCD是菱形
A
B
C
D
菱形ABCD
方
法
归
纳
有一组邻边相等的平行四边形是菱形.
菱形的判定方法1:
探
究
新
知
菱形的特殊性质
逆命题
四条边都相等
的 是菱形
菱形的四条
边都相等
?
对角线互相垂的
是菱形
菱形的对角线
互相平分
?
猜想1
猜想2
四边形
平行四边形
已知:在四边形ABCD中,AB=BC=CD=DA
证明:
在四边形ABCD中
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=AD,
∴四边形ABCD是菱形
A
B
C
D
猜想:四边都相等的四边形是菱形
求证:四边形ABCD是菱形
验
证
猜
想
几何语言
方
法
归
纳
在四边形ABCD中∵AB=BC=CD=DA
∴四边形ABCD是菱形
A
B
C
D
菱形ABCD
菱形的判定方法2:
四边形
四条边相等 是菱形
验
证
猜
想
猜想:对角线互相垂直的平行四边形是菱形
已知:在 中,AC ⊥BD 于点O
ABCD
求证: 是菱形
ABCD
证明:
∵ 四边形ABCD是平行四边形
又∵ AC ⊥BD于点O
∴OA=OC
∴∠DOA=∠DOC=90°
OA=OC
∠DOA=∠DOC
OD=OD
∴△AOD≌△DOC(SAS)
在△DOA和△DOC中
∴ DA=DC
D
C
B
A
O
┓
∴ ABCD是菱形
{
(有一组邻边相等的平行四边形叫做菱形)
验
证
猜
想
猜想:对角线互相垂直的平行四边形是菱形
已知:在 中,AC ⊥BD 于点O
ABCD
求证: 是菱形
ABCD
证明:
∵ 四边形ABCD是平行四边形
又∵ AC ⊥BD于点O
∴ OA=OC
∴ DA=DC
D
C
B
A
O
┓
∴ ABCD是菱形
(线段垂直平分线上的点,到线段两个端点的距离相等)
(有一组邻边相等的平行四边形叫做菱形)
几何语言
方
法
归
纳
∵ 四边形ABCD是平行四边形
又∵AC⊥BD于点O;
∴□ ABCD是菱形
菱形的判定方法3:
对角线互相垂直的 是菱形
平行四边形
A
B
C
D
菱形ABCD
O
方
法
归
纳
①有一组邻边相等
②对角线互相垂直
四条边相等的四边形是菱形
判定菱形时,要注意是从“四边形”出发,还是从“平行四边形”出发这个前提条件
明
辨
是
非
1.有一组邻边相等的四边形是菱形。
2.对角线互相平分且邻边相等的四边形是菱形。
3.有三边相等的四边形是菱形。
4.对角线互相垂直的四边形是菱形。
5.对角线互相垂直且平分的四边形是菱形。
判断下列命题是否正确,错误的请改正.
①先判定平行四边形;
②再寻找一个条件.
活
学
活
用
如图,在四边形ABCD中,已知AB∥ CD,
AB=CD,在不添加任何辅助线的前提下,请你添加一个适当的条件,使四边形ABCD是菱形 : (只需添加一个即可)
A
B
C
D
O
体验之旅----努力造就实力
探索之旅----态度决定高度
智慧之旅----善用内在潜能
闯关之旅----拼搏成就梦想
四条边都相等
菱形
一组邻边相等
对角线互相垂直
对角线互相平分
一组对边平行且相等
二组对边平行或相等
四边形
平行四边形
两组对角相等
善于总结是学习的前提条件
我的收获----
数学课上,老师让同学们判断一个四边形是否为菱形,下面是某合作小组4名同学拟定的方案,其中正确的是 ( )
A.测量对角线是否相等
B.测量对角线是否垂直
C.测量一组对角是否相等
D.测量四边是否相等
D
(四条边都相等的四边形是菱形)
体验之旅----努力造就实力
如图, ABCD 的对角线AC、BD相交于点O,
且AO=3,BO=4,AB=5.
求证: ABCD是菱形.
A
B
C
D
O
证明:∵ AO=3,BO=4,AB=5
∴AB2=AO2+BO2
∴△OAB是直角三角形
∴AC⊥BD于点O
又∵四边形ABCD是平行四边形
∴四边形ABCD是菱形
(对角线互相垂直的平行四边形是菱形)
探索之旅----态度决定高度
∴AO2+BO2=32+42=25,AB2=25
已知:如图,AD平分∠BAC,DE∥AC 交AB
于E,DF∥AB交AC于F.
求证:四边形AEDF是菱形.
∴ □AEDF是菱形
∵DE∥AC DF∥AB
∴四边形AEDF是平行四边形
∵ DE∥AC∴∠2=∠3
∵ AD平分∠BAC∴ ∠1=∠2
∴AE=DE
∴ ∠1=∠3
证明:
(一组邻边相等的平行四边形是菱形)
A
B
C
F
D
E
1
2
3
智慧之旅----善用内在潜能
(2018.新疆中考)
如图,在矩形ABCD中,点P是线段AD上的一个动点,O是BD的中点,PO的延长线交BC于点Q。
(1)求证:四边形PBQD是平行四边形;
(2)若AD=6cm,AB=4cm,P从A出发以1cm/s的速度向D运动(不于D重合),设点P运动的时间为t秒。
①请用t表示PD的长;
②当t为何值时,四边形
PBQD是菱形。
C
B
D
P
O
A
Q
闯关之旅----拼搏成就梦想
四条边都相等
菱形
一组邻边相等
对角线互相垂直
对角线互相平分
一组对边平行且相等
二组对边平行或相等
四边形
平行四边形
两组对角相等
善于总结是学习的前提条件
我的收获----
菱形的判定
已知平行四边形,邻边相等叫菱形;
两对角线若垂直,顺理成章成菱形 。
任意一个四边形,四边相等叫菱形;
四边形的对角线,垂直平分是菱形 。
我
有
绝
招
1.大练习册一个课时
2.导学案--课后练习 ①必做 ②选做
分
层
作
业
如图,两张等宽的纸条交叉重叠在一起,重叠的部分ABCD是菱形吗?求证:
(1)四边形ABCD是平行四边形
(2)过A作AE⊥BC于E点, 过A作AF⊥CD 于F.用等积法说明BC=CD.
(3)求证:四边形ABCD是菱形.
A
C
D
B
奇妙之旅----
D
C
B
A
解:过点A作AE⊥BC于点E,AF⊥CD于点F
∵ 两纸条的宽度相同
∴ AE=AF
由题意可知:AB∥CD, AD∥BC
∴ 四边形ABCD是平行四边形
∵ S ABCD=BC ? AE=CD? AF
又 ∵ AE=AF
∴ BC=CD
∴ 四边形ABCD是菱形
如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形。
H
G
F
E
D
C
B
A
证明:连接AC、BD
∵四边形ABCD是矩形
∴AC=BD
∵点E、F、G、H为各边中点
∴EF=FG=GH=HE
∴四边形EFGH是菱形
收获之旅----
中点四边形
