第三章 变量之间的关系检测题(含答案)
文档属性
| 名称 | 第三章 变量之间的关系检测题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 450.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 07:57:43 | ||
图片预览



文档简介
21世纪教育网
–全国领先的中小学教育资源及组卷应用平台
北师大版2020-2021学年度下学期七年级数学(下册)
第三章变量之间的关系检测题
(有答案)
(时间:100分钟
满分:120分)
一、选择题
(每小题3分,共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
1、鱼是变温动物,又叫冷血动物.它们的体温随水温改变而变化,
在这一问题中,自变量是(
)
A.水深
B.体温
C.水温
D.时间
2、某承包队承接一条长210km的河道清淤工程,预计工期为140天,若每天清淤的长度保持不变,则还未完成的河道长度y(km)与施工时间x(天)之间的关系式为(
)
A.y=210?x?
?B.y=140x?210?
C.y=30?x??
D.y=210+x
3、某人利用计算机设计了一个程序,输入和输出的数据如下表:那么,当输入数据9时,输出的数据是(
)
输入
…
1
2
3
4
5
6
…
输出
…
…
A.
B.
C.
D.
4、在关系式y=5x?16中,下列说法:①x是自变量,y是因变量,5、?6是常量;②x可以取任何数值;③y是变量,5x与?16是常量;④y与x的关系还可以用列表法和图象法表示;⑤当y=?1时,x=?3.其中说法正确的是(
)
A.①②④
B.①②⑤
C.①③⑤
D.②④⑤
5、在球体的公式V=中,常量与变量分别是(
)
A.3、是常量,V、π、R是变量
B.是常量,V、R是变量
C.3、是常量,R是变量
D.3、是常量,V、R是变量
6、某地海拔高度h与温度T的关系可用T=20?6h来表示(其中温度单位℃,海拔高度单位为千米),则该地区某海拔高度为2500米的山顶上的温度为( )
A.6℃
B.5℃
C.4℃
D.3℃
7、已知△ABC的底边BC上的高为10cm,当它的底边BC从20cm变化到8cm时,△ABC的面
积(
)
A.从80cm
2
变化到160cm
2
B.从100cm
2
变化到40cm
2
C.从200cm
2
变化到80cm
2
D.从80cm
2
变化到200cm
2
8、某人从家出发到超市购物,购物后这个人到售报亭买报纸,然后回家.如图描述了这个人在购物过程中离家的距离s(米)与购物所用的时间t(分)之间的函数关系,用一个曲线图直观的表示出来.根据图象,下列信息错误的是(
)
A.这个人购物用时20分钟
B.超市阅报栏距这个人家240米
C.这个人购物后去报停用时10分钟
D.这个人从报停回家的速度为每分钟48米
9、在一条笔直的高速公路上依次有A、B、C三个服务区,一辆轿车从A出发,沿直线匀速行驶经过B服务区向C服务区进发,最终达到C服务区,设行驶x
(h)后,辆轿与B服务区的距离为y
(km),
y与x的关系如图所示,则下列说法正确的是(?
?)
A.B、C两个服务区的距离是120km
B.小轿车在B服务区休息了0.4小时
C.从B服务区到达C服务区共花了1.2小时
D.小轿车的行驶速度是90km/h
10、一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15km/h,水流速度为5km/h.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t(h),航行的路程为s(km),则s与t的函数图象大致是( )
二、填空题
(每题3分,共30分)
11、在一定高度,一个物体自由下落的距离h(m)与下落时间t(s)的关系为h=(g为重力加速度,g=9.8m/s2),在这个变化过程中,
是自变量,
是因变量.
12、在一个边长为4的正方形中挖去一个边长为x(0.
13、如图所示是关于变量x,y的程序计算,若开始输入的x值为?3,则最后输出因变量y的值为___.
14、某志愿者团队乘汽车赴450km外的农村小学参加活动,全程的前一部分为高速公路,后一部分
为乡村公路.若汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路
程y
(单位:km
)与时间x
(单位:h
)之间的关系如图所示,与下列结论:
①汽车在高速公路上的行驶速度为90km/h;②乡村公路总长为90km;
③汽车在乡村公路上的行驶速度为60km/h;
④该团队在出发后7.5h到达采访地;⑤该团队在高速公路上与在乡村公路上所用的时间相同.
其中正确的是
(填正确的序号)
15、用火柴棒摆“三角形”,如图所示:按照规律,第6个图形中需要火柴棒的根数是
.
16、把y=3(x+4)(x?2)
?2(x?3)(x+3)
?
(x?5)2化成y=ax+b的形式为
.
17、A、B两地相距48千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系,下列说法:①甲早出发了1.5小时;②乙出发4.5小时后追上甲;③甲的速度是4千米/小时;④乙先到达B地.其中正确的个数是
.
?
18、婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍;以上叙述中,自变量是
,因变量是
.
19、一个装有进水管和出水管的容器,从某一时刻起只打开进水管进水,经过一段时间,再打开出水管放水,至9分钟时,关停进水管.在打开进水管到关停进水管这段时间内,容器内的水量y(单位:升)与时间x(单位:分钟)之间的函数关系如图所示,关停进水管后,经过
分钟,容器中的水恰好放完.
20、小明和爸爸去爬山,他们从家里出发,爸爸骑摩托车,小明步行,图中的函数图象表示的是小明和爸爸行驶的过程(x表示小明从家出发所行的时间,y1表示小明所行的路程,y2表示爸爸所行的路程).有下列说法:
①小明的家与山的路程为2?000米;
②小明和爸爸同时从起点出发;
③小明在途中休息了20分钟;
④爸爸全程用了20分钟;
⑤小明和爸爸同时到达终点.
其中正确的说法是
.(把你认为正确说法的序号都填上)
三、解答题(共6题
共60分)
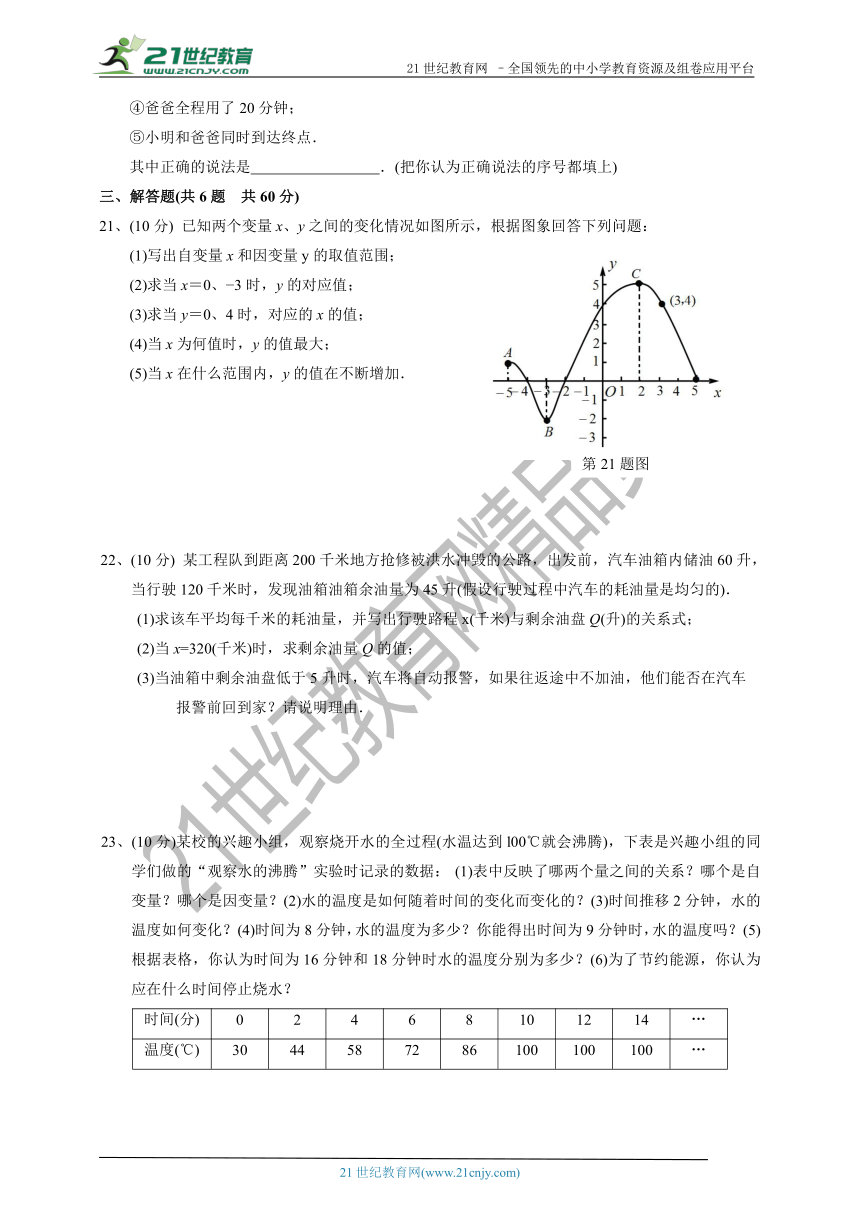
21、(10分)
已知两个变量x、y之间的变化情况如图所示,根据图象回答下列问题:
(1)写出自变量x和因变量y的取值范围;
(2)求当x=0、?3时,y的对应值;
(3)求当y=0、4时,对应的x的值;
(4)当x为何值时,y的值最大;
(5)当x在什么范围内,y的值在不断增加.
22、(10分)
某工程队到距离200千米地方抢修被洪水冲毁的公路,出发前,汽车油箱内储油60升,当行驶120千米时,发现油箱油箱余油量为45升(假设行驶过程中汽车的耗油量是均匀的).
(1)求该车平均每千米的耗油量,并写出行驶路程x(千米)与剩余油盘Q(升)的关系式;
(2)当x=320(千米)时,求剩余油量Q的值;
(3)当油箱中剩余油盘低于5升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车
报警前回到家?请说明理由.
?
23、(10分)某校的兴趣小组,观察烧开水的全过程(水温达到l00℃就会沸腾),下表是兴趣小组的同学们做的“观察水的沸腾”实验时记录的数据:
(1)表中反映了哪两个量之间的关系?哪个是自变量?哪个是因变量?(2)水的温度是如何随着时间的变化而变化的?(3)时间推移2分钟,水的温度如何变化?(4)时间为8分钟,水的温度为多少?你能得出时间为9分钟时,水的温度吗?(5)根据表格,你认为时间为16分钟和18分钟时水的温度分别为多少?(6)为了节约能源,你认为应在什么时间停止烧水?时间(分)
0
2
4
6
8
10
12
14
…
温度(℃)
30
44
58
72
86
100
100
100
…
24、(9分)
在一节弹簧秤测量物体重量的实验课上,第1小组把一根弹簧的上端按要求固定、在其下端悬挂物体,下表是测得的弹簧的长度y(cm)与所挂物体质量x(kg)的一组对应值的记录情况:
所挂物体质量x/kg
0
1
2
3
4
5
弹簧长度y/cm
15
18
21
24
27
30
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当所挂物体重量为4
kg时,弹簧伸长多少?不挂重物时呢?
(3)若所挂重物为8
kg时(在允许范围内),你能说出此时的弹簧长度吗?
25、(9分)
某机械公司生产一种轴承,由于产量较大需要租借仓库存放,经过调研得知,甲仓库的租用条件是每件4元,外加20000元月租费;乙仓库的租用条件是每件8元,无需月租费.
(1)分别写出甲、乙仓库的收费y甲(元)、y乙(元)与轴承的数量x(件)之间的关系式;
(2)存放数量为多少件时,仓库的费用相同?
(3)若存放轴承7000件,选择甲、乙哪个仓库比较合算.
26、(12分)
某市为打造交通枢纽城市,现有A,B两地之间的中心地段的公路需要修建,甲、乙两工程队共同承包,两队分别从A,B两地相向施工.已知甲队先施工3天,乙队才开始施工,乙队施工几天后因另有紧急任务暂停施工,因考虑工期,由甲队以原速的2倍修建,乙队完成紧急任务后又以原速恢复施工,直到道路修通.甲,乙两队各自修路长度与时间之间的关系如图所示,请结合图中信息解答下列问题:
?
(1)试问:在施工的过程中,甲队在提速前每天修道路多少米?
?
(2)求乙队中途暂停施工的天数;
(3)求A,B两地之间的道路长度.
参考答案
一、选择题(共10小题
每3分
共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
A
D
A
B
C
B
D
C
D
二、填空题(共10小题
每题3分
共30分)
11、t、h
12、y=16
?
x2
13、①③⑤
14、42
15、33
16、y=16x?31
17、
①③④
18、年龄、体重
19、6
20、①③④
三、解答题(共6题
共60分)
21、(10分)
已知两个变量x、y之间的变化情况如图所示,根据图象回答下列问题:
(1)写出自变量x和因变量y的取值范围;
(2)求当x=0、?3时,y的对应值;
(3)求当y=0、4时,对应的x的值;
(4)当x为何值时,y的值最大;
(5)当x在什么范围内,y的值在不断增加.
解:(1)根据函数图象可得:自变量x的取值范围
是?5~5,因变量y的变化范围为?2~5.
(2)当x=0时,y=4;当x=
?5时,y=1.
(3)当y=0时,x1=
?4,x2=
?2,x3=5;
当y=4时,x1=0,x2=3.
(4)当x=2时,图象有最高点,此时y的值最大.
(5)当x在?3~2范围内时,函数图象上升,y的值在不断增加.
22、(9分)
某工程队到距离200千米地方抢修被洪水冲毁的公路,出发前,汽车油箱内储油60升,当行驶120千米时,发现油箱油箱余油量为45升(假设行驶过程中汽车的耗油量是均匀的).
(1)求该车平均每千米的耗油量,并写出行驶路程x(千米)与剩余油盘Q(升)的关系式;
(2)当x=320(千米)时,求剩余油量Q的值;
(3)当油箱中剩余油盘低于5升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车
报警前回到家?请说明理由.
?
解:(1)该车平均每千米的耗油量为(60?45)÷120=0.125(升/千米),
行驶路程x(千米)与剩余油盘Q(升)的关系式为Q=60?0.125x;
(2)当x=320时,Q=60?0.1×320=20(L).
答:当x=320(千米)时,剩余油量Q的值为20L.
(3)(60?5)÷0.125=440(千米),
∵440>400,
∴他们能在汽车报警前回到家.
23、(10分)某校的兴趣小组,观察烧开水的全过程(水温达到l00℃就会沸腾),下表是兴趣小组的同学们做的“观察水的沸腾”实验时记录的数据:
(1)表中反映了哪两个量之间的关系?哪个是自变量?哪个是因变量?(2)水的温度是如何随着时间的变化而变化的?(3)时间推移2分钟,水的温度如何变化?(4)时间为8分钟,水的温度为多少?你能得出时间为9分钟时,水的温度吗?(5)根据表格,你认为时间为16分钟和18分钟时水的温度分别为多少?(6)为了节约能源,你认为应在什么时间停止烧水?
时间(分)
0
2
4
6
8
10
12
14
…
温度(℃)
30
44
58
72
86
100
100
100
…
(1)此表反映了水的温度与时间的关系,时间是自变量,水的温度是因变量;
(2)水的温度随着时间的增加而增加,到100℃时恒定;
(3)时间推移2分钟,水的温度增加14度,到10分钟时恒定;
(4)时间为8分钟,水的温度是86℃,时间为9分钟,水的温度是93℃;
(5)根据表格,时间为16分钟和18分钟时水的温度均为100℃;
(6)为了节约能源,应在10钟后停止烧水.
24、(10分)
在一节弹簧秤测量物体重量的实验课上,第1小组把一根弹簧的上端按要求固定、在其下端悬挂物体,下表是测得的弹簧的长度y(cm)与所挂物体质量x(kg)的一组对应值的记录情况:
所挂物体质量x/kg
0
1
2
3
4
5
弹簧长度y/cm
15
18
21
24
27
30
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当所挂物体重量为4
kg时,弹簧伸长多少?不挂重物时呢?
(3)若所挂重物为8
kg时(在允许范围内),你能说出此时的弹簧长度吗?
解:(1)上表反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量,弹簧长度是因变量;
(2)当所挂物体重量为4
kg时,弹簧伸长9
cm;当不挂重物时,弹簧长15
cm;
(3)根据上表可知所挂重物为8
kg时(在允许范围内)时的弹簧长度=15+3×8=39
cm.
25、(9分)
某机械公司生产一种轴承,由于产量较大需要租借仓库存放,经过调研得知,甲仓库的租用条件是每件4元,外加20000元月租费;乙仓库的租用条件是每件8元,无需月租费.
(1)分别写出甲、乙仓库的收费y甲(元)、y乙(元)与轴承的数量x(件)之间的关系式;
(2)存放数量为多少件时,仓库的费用相同?
(3)若存放轴承7000件,选择甲、乙哪个仓库比较合算.
解:(1)y1=4x+20000,y2=8x
(2)存放数量为x件时
4x+20000=8x
4x=20000
x=5000;
答:存放数量为5000件时,仓库的费用相同;
(3)第一种方式:4×7000+20000=28000+20000=48000,
第二种方式:8×7000=56000,
∵56000>48000.
∴第一种方式合算
26、(12分)
某市为打造交通枢纽城市,现有A,B两地之间的中心地段的公路需要修建,甲、乙两工程队共同承包,两队分别从A,B两地相向施工.已知甲队先施工3天,乙队才开始施工,乙队施工几天后因另有紧急任务暂停施工,因考虑工期,由甲队以原速的2倍修建,乙队完成紧急任务后又以原速恢复施工,直到道路修通.甲,乙两队各自修路长度与时间之间的关系如图所示,请结合图中信息解答下列问题:
?
(1)试问:在施工的过程中,甲队在提速前每天修道路多少米?
?
(2)求乙队中途暂停施工的天数;
(3)求A,B两地之间的道路长度.
解:(1)设甲队在提速前每天修道路x米,
根据题意,
得:5x=440,
?
解得:x=88,
?
即甲队在提速前每天修道路88米;
?
(2)根据题意,
乙队的速度为(440)÷(5?3)=220(米/天),
?
设乙队中途暂停施工的天数为t,可得:220×(6?3)+[11?(6+t)]=1100,
解得:t=3,
?
即乙队中途暂停施工的天数为3天;
?(3)由(1)知,甲队提速前的施工速度为88米/天,则提速后甲队是速度为
88×2=176(米/天),
?
设AB两地之间长度为y,
?则y=88×6+176×(11?6)+1100,
解得:y=2508,
?
则AB两地之间长度为2508米.
第8题图
第26题图
小明
爸爸
第26题图
第21题图
第20题图
(1)
(2)
(3)
第19题图
第17题图
第15题图
A
B
C
D
第14题图
第21题图
第13题图
第9题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
–全国领先的中小学教育资源及组卷应用平台
北师大版2020-2021学年度下学期七年级数学(下册)
第三章变量之间的关系检测题
(有答案)
(时间:100分钟
满分:120分)
一、选择题
(每小题3分,共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
1、鱼是变温动物,又叫冷血动物.它们的体温随水温改变而变化,
在这一问题中,自变量是(
)
A.水深
B.体温
C.水温
D.时间
2、某承包队承接一条长210km的河道清淤工程,预计工期为140天,若每天清淤的长度保持不变,则还未完成的河道长度y(km)与施工时间x(天)之间的关系式为(
)
A.y=210?x?
?B.y=140x?210?
C.y=30?x??
D.y=210+x
3、某人利用计算机设计了一个程序,输入和输出的数据如下表:那么,当输入数据9时,输出的数据是(
)
输入
…
1
2
3
4
5
6
…
输出
…
…
A.
B.
C.
D.
4、在关系式y=5x?16中,下列说法:①x是自变量,y是因变量,5、?6是常量;②x可以取任何数值;③y是变量,5x与?16是常量;④y与x的关系还可以用列表法和图象法表示;⑤当y=?1时,x=?3.其中说法正确的是(
)
A.①②④
B.①②⑤
C.①③⑤
D.②④⑤
5、在球体的公式V=中,常量与变量分别是(
)
A.3、是常量,V、π、R是变量
B.是常量,V、R是变量
C.3、是常量,R是变量
D.3、是常量,V、R是变量
6、某地海拔高度h与温度T的关系可用T=20?6h来表示(其中温度单位℃,海拔高度单位为千米),则该地区某海拔高度为2500米的山顶上的温度为( )
A.6℃
B.5℃
C.4℃
D.3℃
7、已知△ABC的底边BC上的高为10cm,当它的底边BC从20cm变化到8cm时,△ABC的面
积(
)
A.从80cm
2
变化到160cm
2
B.从100cm
2
变化到40cm
2
C.从200cm
2
变化到80cm
2
D.从80cm
2
变化到200cm
2
8、某人从家出发到超市购物,购物后这个人到售报亭买报纸,然后回家.如图描述了这个人在购物过程中离家的距离s(米)与购物所用的时间t(分)之间的函数关系,用一个曲线图直观的表示出来.根据图象,下列信息错误的是(
)
A.这个人购物用时20分钟
B.超市阅报栏距这个人家240米
C.这个人购物后去报停用时10分钟
D.这个人从报停回家的速度为每分钟48米
9、在一条笔直的高速公路上依次有A、B、C三个服务区,一辆轿车从A出发,沿直线匀速行驶经过B服务区向C服务区进发,最终达到C服务区,设行驶x
(h)后,辆轿与B服务区的距离为y
(km),
y与x的关系如图所示,则下列说法正确的是(?
?)
A.B、C两个服务区的距离是120km
B.小轿车在B服务区休息了0.4小时
C.从B服务区到达C服务区共花了1.2小时
D.小轿车的行驶速度是90km/h
10、一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15km/h,水流速度为5km/h.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t(h),航行的路程为s(km),则s与t的函数图象大致是( )
二、填空题
(每题3分,共30分)
11、在一定高度,一个物体自由下落的距离h(m)与下落时间t(s)的关系为h=(g为重力加速度,g=9.8m/s2),在这个变化过程中,
是自变量,
是因变量.
12、在一个边长为4的正方形中挖去一个边长为x(0
13、如图所示是关于变量x,y的程序计算,若开始输入的x值为?3,则最后输出因变量y的值为___.
14、某志愿者团队乘汽车赴450km外的农村小学参加活动,全程的前一部分为高速公路,后一部分
为乡村公路.若汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路
程y
(单位:km
)与时间x
(单位:h
)之间的关系如图所示,与下列结论:
①汽车在高速公路上的行驶速度为90km/h;②乡村公路总长为90km;
③汽车在乡村公路上的行驶速度为60km/h;
④该团队在出发后7.5h到达采访地;⑤该团队在高速公路上与在乡村公路上所用的时间相同.
其中正确的是
(填正确的序号)
15、用火柴棒摆“三角形”,如图所示:按照规律,第6个图形中需要火柴棒的根数是
.
16、把y=3(x+4)(x?2)
?2(x?3)(x+3)
?
(x?5)2化成y=ax+b的形式为
.
17、A、B两地相距48千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系,下列说法:①甲早出发了1.5小时;②乙出发4.5小时后追上甲;③甲的速度是4千米/小时;④乙先到达B地.其中正确的个数是
.
?
18、婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍;以上叙述中,自变量是
,因变量是
.
19、一个装有进水管和出水管的容器,从某一时刻起只打开进水管进水,经过一段时间,再打开出水管放水,至9分钟时,关停进水管.在打开进水管到关停进水管这段时间内,容器内的水量y(单位:升)与时间x(单位:分钟)之间的函数关系如图所示,关停进水管后,经过
分钟,容器中的水恰好放完.
20、小明和爸爸去爬山,他们从家里出发,爸爸骑摩托车,小明步行,图中的函数图象表示的是小明和爸爸行驶的过程(x表示小明从家出发所行的时间,y1表示小明所行的路程,y2表示爸爸所行的路程).有下列说法:
①小明的家与山的路程为2?000米;
②小明和爸爸同时从起点出发;
③小明在途中休息了20分钟;
④爸爸全程用了20分钟;
⑤小明和爸爸同时到达终点.
其中正确的说法是
.(把你认为正确说法的序号都填上)
三、解答题(共6题
共60分)
21、(10分)
已知两个变量x、y之间的变化情况如图所示,根据图象回答下列问题:
(1)写出自变量x和因变量y的取值范围;
(2)求当x=0、?3时,y的对应值;
(3)求当y=0、4时,对应的x的值;
(4)当x为何值时,y的值最大;
(5)当x在什么范围内,y的值在不断增加.
22、(10分)
某工程队到距离200千米地方抢修被洪水冲毁的公路,出发前,汽车油箱内储油60升,当行驶120千米时,发现油箱油箱余油量为45升(假设行驶过程中汽车的耗油量是均匀的).
(1)求该车平均每千米的耗油量,并写出行驶路程x(千米)与剩余油盘Q(升)的关系式;
(2)当x=320(千米)时,求剩余油量Q的值;
(3)当油箱中剩余油盘低于5升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车
报警前回到家?请说明理由.
?
23、(10分)某校的兴趣小组,观察烧开水的全过程(水温达到l00℃就会沸腾),下表是兴趣小组的同学们做的“观察水的沸腾”实验时记录的数据:
(1)表中反映了哪两个量之间的关系?哪个是自变量?哪个是因变量?(2)水的温度是如何随着时间的变化而变化的?(3)时间推移2分钟,水的温度如何变化?(4)时间为8分钟,水的温度为多少?你能得出时间为9分钟时,水的温度吗?(5)根据表格,你认为时间为16分钟和18分钟时水的温度分别为多少?(6)为了节约能源,你认为应在什么时间停止烧水?时间(分)
0
2
4
6
8
10
12
14
…
温度(℃)
30
44
58
72
86
100
100
100
…
24、(9分)
在一节弹簧秤测量物体重量的实验课上,第1小组把一根弹簧的上端按要求固定、在其下端悬挂物体,下表是测得的弹簧的长度y(cm)与所挂物体质量x(kg)的一组对应值的记录情况:
所挂物体质量x/kg
0
1
2
3
4
5
弹簧长度y/cm
15
18
21
24
27
30
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当所挂物体重量为4
kg时,弹簧伸长多少?不挂重物时呢?
(3)若所挂重物为8
kg时(在允许范围内),你能说出此时的弹簧长度吗?
25、(9分)
某机械公司生产一种轴承,由于产量较大需要租借仓库存放,经过调研得知,甲仓库的租用条件是每件4元,外加20000元月租费;乙仓库的租用条件是每件8元,无需月租费.
(1)分别写出甲、乙仓库的收费y甲(元)、y乙(元)与轴承的数量x(件)之间的关系式;
(2)存放数量为多少件时,仓库的费用相同?
(3)若存放轴承7000件,选择甲、乙哪个仓库比较合算.
26、(12分)
某市为打造交通枢纽城市,现有A,B两地之间的中心地段的公路需要修建,甲、乙两工程队共同承包,两队分别从A,B两地相向施工.已知甲队先施工3天,乙队才开始施工,乙队施工几天后因另有紧急任务暂停施工,因考虑工期,由甲队以原速的2倍修建,乙队完成紧急任务后又以原速恢复施工,直到道路修通.甲,乙两队各自修路长度与时间之间的关系如图所示,请结合图中信息解答下列问题:
?
(1)试问:在施工的过程中,甲队在提速前每天修道路多少米?
?
(2)求乙队中途暂停施工的天数;
(3)求A,B两地之间的道路长度.
参考答案
一、选择题(共10小题
每3分
共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
A
D
A
B
C
B
D
C
D
二、填空题(共10小题
每题3分
共30分)
11、t、h
12、y=16
?
x2
13、①③⑤
14、42
15、33
16、y=16x?31
17、
①③④
18、年龄、体重
19、6
20、①③④
三、解答题(共6题
共60分)
21、(10分)
已知两个变量x、y之间的变化情况如图所示,根据图象回答下列问题:
(1)写出自变量x和因变量y的取值范围;
(2)求当x=0、?3时,y的对应值;
(3)求当y=0、4时,对应的x的值;
(4)当x为何值时,y的值最大;
(5)当x在什么范围内,y的值在不断增加.
解:(1)根据函数图象可得:自变量x的取值范围
是?5~5,因变量y的变化范围为?2~5.
(2)当x=0时,y=4;当x=
?5时,y=1.
(3)当y=0时,x1=
?4,x2=
?2,x3=5;
当y=4时,x1=0,x2=3.
(4)当x=2时,图象有最高点,此时y的值最大.
(5)当x在?3~2范围内时,函数图象上升,y的值在不断增加.
22、(9分)
某工程队到距离200千米地方抢修被洪水冲毁的公路,出发前,汽车油箱内储油60升,当行驶120千米时,发现油箱油箱余油量为45升(假设行驶过程中汽车的耗油量是均匀的).
(1)求该车平均每千米的耗油量,并写出行驶路程x(千米)与剩余油盘Q(升)的关系式;
(2)当x=320(千米)时,求剩余油量Q的值;
(3)当油箱中剩余油盘低于5升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车
报警前回到家?请说明理由.
?
解:(1)该车平均每千米的耗油量为(60?45)÷120=0.125(升/千米),
行驶路程x(千米)与剩余油盘Q(升)的关系式为Q=60?0.125x;
(2)当x=320时,Q=60?0.1×320=20(L).
答:当x=320(千米)时,剩余油量Q的值为20L.
(3)(60?5)÷0.125=440(千米),
∵440>400,
∴他们能在汽车报警前回到家.
23、(10分)某校的兴趣小组,观察烧开水的全过程(水温达到l00℃就会沸腾),下表是兴趣小组的同学们做的“观察水的沸腾”实验时记录的数据:
(1)表中反映了哪两个量之间的关系?哪个是自变量?哪个是因变量?(2)水的温度是如何随着时间的变化而变化的?(3)时间推移2分钟,水的温度如何变化?(4)时间为8分钟,水的温度为多少?你能得出时间为9分钟时,水的温度吗?(5)根据表格,你认为时间为16分钟和18分钟时水的温度分别为多少?(6)为了节约能源,你认为应在什么时间停止烧水?
时间(分)
0
2
4
6
8
10
12
14
…
温度(℃)
30
44
58
72
86
100
100
100
…
(1)此表反映了水的温度与时间的关系,时间是自变量,水的温度是因变量;
(2)水的温度随着时间的增加而增加,到100℃时恒定;
(3)时间推移2分钟,水的温度增加14度,到10分钟时恒定;
(4)时间为8分钟,水的温度是86℃,时间为9分钟,水的温度是93℃;
(5)根据表格,时间为16分钟和18分钟时水的温度均为100℃;
(6)为了节约能源,应在10钟后停止烧水.
24、(10分)
在一节弹簧秤测量物体重量的实验课上,第1小组把一根弹簧的上端按要求固定、在其下端悬挂物体,下表是测得的弹簧的长度y(cm)与所挂物体质量x(kg)的一组对应值的记录情况:
所挂物体质量x/kg
0
1
2
3
4
5
弹簧长度y/cm
15
18
21
24
27
30
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当所挂物体重量为4
kg时,弹簧伸长多少?不挂重物时呢?
(3)若所挂重物为8
kg时(在允许范围内),你能说出此时的弹簧长度吗?
解:(1)上表反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量,弹簧长度是因变量;
(2)当所挂物体重量为4
kg时,弹簧伸长9
cm;当不挂重物时,弹簧长15
cm;
(3)根据上表可知所挂重物为8
kg时(在允许范围内)时的弹簧长度=15+3×8=39
cm.
25、(9分)
某机械公司生产一种轴承,由于产量较大需要租借仓库存放,经过调研得知,甲仓库的租用条件是每件4元,外加20000元月租费;乙仓库的租用条件是每件8元,无需月租费.
(1)分别写出甲、乙仓库的收费y甲(元)、y乙(元)与轴承的数量x(件)之间的关系式;
(2)存放数量为多少件时,仓库的费用相同?
(3)若存放轴承7000件,选择甲、乙哪个仓库比较合算.
解:(1)y1=4x+20000,y2=8x
(2)存放数量为x件时
4x+20000=8x
4x=20000
x=5000;
答:存放数量为5000件时,仓库的费用相同;
(3)第一种方式:4×7000+20000=28000+20000=48000,
第二种方式:8×7000=56000,
∵56000>48000.
∴第一种方式合算
26、(12分)
某市为打造交通枢纽城市,现有A,B两地之间的中心地段的公路需要修建,甲、乙两工程队共同承包,两队分别从A,B两地相向施工.已知甲队先施工3天,乙队才开始施工,乙队施工几天后因另有紧急任务暂停施工,因考虑工期,由甲队以原速的2倍修建,乙队完成紧急任务后又以原速恢复施工,直到道路修通.甲,乙两队各自修路长度与时间之间的关系如图所示,请结合图中信息解答下列问题:
?
(1)试问:在施工的过程中,甲队在提速前每天修道路多少米?
?
(2)求乙队中途暂停施工的天数;
(3)求A,B两地之间的道路长度.
解:(1)设甲队在提速前每天修道路x米,
根据题意,
得:5x=440,
?
解得:x=88,
?
即甲队在提速前每天修道路88米;
?
(2)根据题意,
乙队的速度为(440)÷(5?3)=220(米/天),
?
设乙队中途暂停施工的天数为t,可得:220×(6?3)+[11?(6+t)]=1100,
解得:t=3,
?
即乙队中途暂停施工的天数为3天;
?(3)由(1)知,甲队提速前的施工速度为88米/天,则提速后甲队是速度为
88×2=176(米/天),
?
设AB两地之间长度为y,
?则y=88×6+176×(11?6)+1100,
解得:y=2508,
?
则AB两地之间长度为2508米.
第8题图
第26题图
小明
爸爸
第26题图
第21题图
第20题图
(1)
(2)
(3)
第19题图
第17题图
第15题图
A
B
C
D
第14题图
第21题图
第13题图
第9题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
