第十章概率单元质量测评 2020-2021学年高一下学期数学人教A版(2019)必修第二册
文档属性
| 名称 | 第十章概率单元质量测评 2020-2021学年高一下学期数学人教A版(2019)必修第二册 |  | |
| 格式 | doc | ||
| 文件大小 | 215.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 21:42:11 | ||
图片预览




文档简介
第十章 单元质量测评
时间:120分钟 满分:150分
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若“A∪B”发生(A,B中至少有一个发生)的概率为0.6,则,同时发生的概率为( )
A.0.6 B.0.36 C.0.24 D.0.4
2.若干个人站成一排,其中为互斥事件的是( )
A.“甲站排头”与“乙站排头”
B.“甲站排头”与“乙不站排尾”
C.“甲站排头”与“乙站排尾”
D.“甲不站排头”与“乙不站排尾”
3.口袋内装有一些大小相同的红球、白球和黑球,从中摸出1个球,摸出红球的概率是0.52,摸出白球的概率是0.28,那么摸出黑球的概率是( )
A.0.2 B.0.28 C.0.52 D.0.8
4.在5盒酸奶中,有2盒已经过了保质期,从中任取2盒,取到的酸奶中有已过保质期的概率为( )
A. B. C. D.
5.从2名男生和2名女生中任意选择两人在星期六、星期日参加某公益活动,每天一人,则星期六安排一名男生、星期日安排一名女生的概率为( )
A. B. C. D.
6.已知A={1,2,3},B={x∈R|x2-ax+b=0,a∈A,b∈A},则事件“A∩B=B”发生的概率是( )
A. B. C. D.1
7.某公司共有职工8000名,从中随机抽取了100名,调查上、下班乘车所用时间,得下表:
所用时间(分钟) [0,20) [20,40) [40,60) [60,80) [80,100]
人数 25 50 15 5 5
公司规定,按照乘车所用时间每月发给职工路途补贴,补贴金额y(元)与乘车时间t(分钟)的关系是y=200+40,其中表示不超过的最大整数.以样本频率为概率,则公司一名职工每月用于路途补贴不超过300元的概率为( )
A.0.5 B.0.7 C.0.8 D.0.9
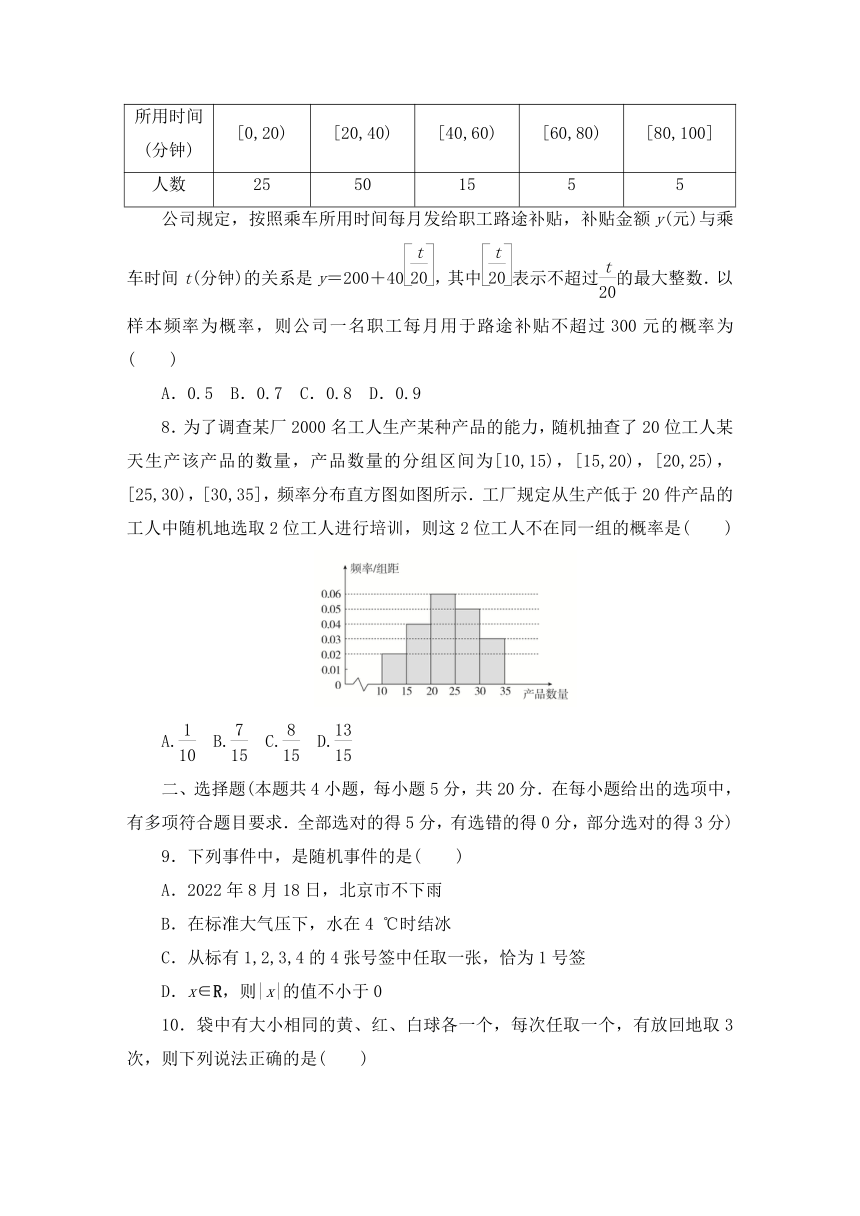
8.为了调查某厂2000名工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35],频率分布直方图如图所示.工厂规定从生产低于20件产品的工人中随机地选取2位工人进行培训,则这2位工人不在同一组的概率是( )
A. B. C. D.
二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分)
9.下列事件中,是随机事件的是( )
A.2022年8月18日,北京市不下雨
B.在标准大气压下,水在4 ℃时结冰
C.从标有1,2,3,4的4张号签中任取一张,恰为1号签
D.x∈R,则|x|的值不小于0
10.袋中有大小相同的黄、红、白球各一个,每次任取一个,有放回地取3次,则下列说法正确的是( )
A.取出的3个球颜色相同的概率为
B.取出的3个球颜色不全相同的概率为
C.取出的3个球颜色全不相同的概率为
D.取出的3个球无红球的概率为
11.某年级有12个班,现要从2班到12班中选1个班的学生参加一项活动,有人提议:掷两个骰子,得到的点数之和是几就选几班,这种选法( )
A.公平,每个班被选到的概率都为
B.不公平,6班被选到的概率最大
C.不公平,2班和12班被选到的概率最小
D.不公平,7班被选到的概率最大
12.甲、乙两个质地均匀且完全一样的四面体,每个面都是正三角形,甲四个面上分别标有数字1,2,3,4,乙四个面上分别标有数字5,6,7,8,同时抛掷这两个四面体一次,记事件A为“两个四面体朝下一面的数字之和为奇数”,事件B为“甲四面体朝下一面的数字为奇数”,事件C为“乙四面体朝下一面的数字为偶数”,则下列结论正确的是( )
A.P(A)=P(B)=P(C)
B.P(BC)=P(AC)=P(AB)
C.P(ABC)=
D.P(A)P(B)P(C)=
三、填空题(本题共4小题,每小题5分,共20分)
13.甲、乙两名运动员各自等可能地从红、白、蓝3种颜色的运动服中选择1种,则他们选择相同颜色运动服的概率为________.
14.A,B,C,D四名学生按任意次序站成一排,则A或B在边上的概率为________.
15.设两个相互独立的事件A与B,若事件A发生的概率为p,事件B发生的概率为1-p,则A与B同时发生的概率的最大值是________.
16.甲、乙两名同学参加一项射击比赛游戏,其中任何一人每射击一次命中目标得2分,未命中目标得0分.若甲、乙两人射击的命中率分别为和p,且甲、乙两人各射击一次得分之和为2的概率为.假设甲、乙两人射击互不影响,则p的值为________,两人各射击一次得分之和不少于2的概率为________.(本题第一空3分,第二空2分)
四、解答题(本题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分10分)已知二次函数f(x)=ax2-bx+1,设集合P={1,2,3},Q={-1,1,2,3,4},分别从集合P和Q中随机取1个数,作为a和b,得到数对(a,b).
(1)列举出所有的数对(a,b),并求函数f(x)有零点的概率;
(2)求函数f(x)在区间[1,+∞)上单调递增的概率.
18.(本小题满分12分)某中学调查了某班全部45名同学参加书法社团和演讲社团的情况,数据如下表(单位:人):
参加书法社团 未参加书法社团
参加演讲社团 8 5
未参加演讲社团 2 30
(1)从该班随机选1名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的8名同学中,有5名男同学A1,A2,A3,A4,A5,3名女同学B1,B2,B3.现从这5名男同学和3名女同学中各随机选1人,求A1被选中且B1未被选中的概率.
19.(本小题满分12分)某地区有小学21所,中学14所,大学7所,现采用比例分配的分层随机抽样的方法从这些学校中抽取6所学校对学生进行视力调查.
(1)求应从小学、中学、大学中分别抽取的学校数目;
(2)若从抽取的6所学校中随机抽取2所学校做进一步数据分析:
①列出所有可能的抽取结果;
②求抽取的2所学校均为小学的概率.
20.(本小题满分12分)袋子中放有大小和形状相同的小球若干个,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个.已知从袋子中随机抽取1个小球,取到标号是2的小球的概率是.
(1)求n的值;
(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为a,第二次取出的小球标号为b.记事件A表示“a+b=2”,求事件A的概率.
21.(本小题满分12分)在某次1500米体能测试中,甲、乙、丙三人各自通过测试的概率分别为,,,求:
(1)3人都通过体能测试的概率;
(2)只有2人通过体能测试的概率;
(3)只有1人通过体能测试的概率.
22.(本小题满分12分)某中学作为蓝色海洋教育特色学校,随机抽取100名学生,进行一次海洋知识测试,按测试成绩(假设考试成绩均在[65,90)内)分组如下:第一组[65,70),第二组[70,75),第三组[75,80),第四组[80,85),第五组[85,90),得到频率分布直方图如图.
(1)求测试成绩在[80,85)内的频率;
(2)从第三、四、五组学生中用比例分配的分层随机抽样的方法抽取6名学生组成海洋知识宣讲小组,定期在校内进行义务宣讲,并在这6名学生中随机选取2名参加市组织的蓝色海洋教育义务宣讲队,求第四组至少有1名学生被抽中的概率.
第十章 单元质量测评
时间:120分钟 满分:150分
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若“A∪B”发生(A,B中至少有一个发生)的概率为0.6,则,同时发生的概率为( )
A.0.6 B.0.36 C.0.24 D.0.4
答案 D
解析 “A∪B”发生指A,B中至少有一个发生,它的对立事件为A,B都不发生,即,同时发生.
2.若干个人站成一排,其中为互斥事件的是( )
A.“甲站排头”与“乙站排头”
B.“甲站排头”与“乙不站排尾”
C.“甲站排头”与“乙站排尾”
D.“甲不站排头”与“乙不站排尾”
答案 A
解析 由互斥事件的定义可得,“甲站排头”与“乙站排头”为互斥事件.
3.口袋内装有一些大小相同的红球、白球和黑球,从中摸出1个球,摸出红球的概率是0.52,摸出白球的概率是0.28,那么摸出黑球的概率是( )
A.0.2 B.0.28 C.0.52 D.0.8
答案 A
解析 设“摸出红球”为事件M,“摸出白球”为事件N,“摸出黑球”为事件E,则P(M)+P(N)+P(E)=1,所以P(E)=1-P(M)-P(N)=1-0.52-0.28=0.2.故选A.
4.在5盒酸奶中,有2盒已经过了保质期,从中任取2盒,取到的酸奶中有已过保质期的概率为( )
A. B. C. D.
答案 C
解析 对5盒酸奶编号1~5,4,5代表过期.从中任取2盒,则样本点有(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5),共10个,这10个样本点出现的可能性相等.含4,5的有7个,所以所求概率为,故选C.
5.从2名男生和2名女生中任意选择两人在星期六、星期日参加某公益活动,每天一人,则星期六安排一名男生、星期日安排一名女生的概率为( )
A. B. C. D.
答案 A
解析 设2名男生记为A1,A2,2名女生记为B1,B2,任意选择两人在星期六、星期日参加某公益活动,有A1A2,A1B1,A1B2,A2B1,A2B2,B1B2,A2A1,B1A1,B2A1,B1A2,B2A2,B2B1,共12种情况,这12种情况发生的可能性是相等的.而星期六安排一名男生、星期日安排一名女生有A1B1,A1B2,A2B1,A2B2,共4种情况,则所求事件发生的概率为P==.故选A.
6.已知A={1,2,3},B={x∈R|x2-ax+b=0,a∈A,b∈A},则事件“A∩B=B”发生的概率是( )
A. B. C. D.1
答案 C
解析 ∵A∩B=B,∴B可能为?,{1},{2},{3},{1,2},{2,3},{1,3}.当B=?时,a2-4b<0,满足条件的a,b为a=1,b=1,2,3;a=2,b=2,3;a=3,b=3.当B={1}时,满足条件的a,b为a=2,b=1.当B={2},{3}时,没有满足条件的a,b.当B={1,2}时,满足条件的a,b为a=3,b=2.当B={2,3},{1,3}时,没有满足条件的a,b,∴事件“A∩B=B”发生的概率为=.故选C.
7.某公司共有职工8000名,从中随机抽取了100名,调查上、下班乘车所用时间,得下表:
所用时间(分钟) [0,20) [20,40) [40,60) [60,80) [80,100]
人数 25 50 15 5 5
公司规定,按照乘车所用时间每月发给职工路途补贴,补贴金额y(元)与乘车时间t(分钟)的关系是y=200+40,其中表示不超过的最大整数.以样本频率为概率,则公司一名职工每月用于路途补贴不超过300元的概率为( )
A.0.5 B.0.7 C.0.8 D.0.9
答案 D
解析 由题意知y≤300,即200+40≤300,即≤2.5,解得0≤t<60,由表可知t∈[0,60)的人数为90,故所求概率为=0.9.
8.为了调查某厂2000名工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35],频率分布直方图如图所示.工厂规定从生产低于20件产品的工人中随机地选取2位工人进行培训,则这2位工人不在同一组的概率是( )
A. B. C. D.
答案 C
解析 根据题中频率分布直方图可知产品件数在[10,15),[15,20)内的人数分别为5×0.02×20=2,5×0.04×20=4,
设生产产品件数在[10,15)内的2人分别是A,B,
设生产产品件数在[15,20)内的4人分别是C,D,E,F,
则从生产低于20件产品的工人中随机地选取2位工人的结果有(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共15种,这15种结果出现的可能性相等.
2位工人不在同一组的结果有(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),共8种.
则选取的这2人不在同一组的概率为.
二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分)
9.下列事件中,是随机事件的是( )
A.2022年8月18日,北京市不下雨
B.在标准大气压下,水在4 ℃时结冰
C.从标有1,2,3,4的4张号签中任取一张,恰为1号签
D.x∈R,则|x|的值不小于0
答案 AC
解析 A,C为随机事件,B为不可能事件,D为必然事件.
10.袋中有大小相同的黄、红、白球各一个,每次任取一个,有放回地取3次,则下列说法正确的是( )
A.取出的3个球颜色相同的概率为
B.取出的3个球颜色不全相同的概率为
C.取出的3个球颜色全不相同的概率为
D.取出的3个球无红球的概率为
答案 BC
解析 有放回地取球3次,共27种可能结果,其中颜色相同的结果有3种,其概率为=,故A错误;颜色不全相同的结果有24种,其概率为=,故B正确;颜色全不相同的结果有6种,其概率为=,故C正确;无红球的结果有8种,其概率为,故D错误.故选BC.
11.某年级有12个班,现要从2班到12班中选1个班的学生参加一项活动,有人提议:掷两个骰子,得到的点数之和是几就选几班,这种选法( )
A.公平,每个班被选到的概率都为
B.不公平,6班被选到的概率最大
C.不公平,2班和12班被选到的概率最小
D.不公平,7班被选到的概率最大
答案 CD
解析 设i班被选到的概率为P(i),i=2,3,4,…,12,则P(2)=P(12)=,P(3)=P(11)=,P(4)=P(10)=,P(5)=P(9)=,P(6)=P(8)=,P(7)=,故选CD.
12.甲、乙两个质地均匀且完全一样的四面体,每个面都是正三角形,甲四个面上分别标有数字1,2,3,4,乙四个面上分别标有数字5,6,7,8,同时抛掷这两个四面体一次,记事件A为“两个四面体朝下一面的数字之和为奇数”,事件B为“甲四面体朝下一面的数字为奇数”,事件C为“乙四面体朝下一面的数字为偶数”,则下列结论正确的是( )
A.P(A)=P(B)=P(C)
B.P(BC)=P(AC)=P(AB)
C.P(ABC)=
D.P(A)P(B)P(C)=
答案 ABD
解析 记(x,y)中的x表示甲四面体朝下一面的数字,y表示乙四面体朝下一面的数字,则所有可能出现的结果为(1,5),(1,6),(1,7),(1,8),(2,5),(2,6),(2,7),(2,8),(3,5),(3,6),(3,7),(3,8),(4,5),(4,6),(4,7),(4,8),共16种,且每种结果出现的可能性相等.满足事件A的结果有8种,则P(A)==,满足事件B的结果有8种,则P(B)==,满足事件C的结果有8种,则P(C)==,则P(A)=P(B)=P(C),故A正确;事件B和事件C同时发生的结果有4种,则P(BC)==,事件A和事件C同时发生的结果有4种,则P(AC)==,事件A和事件B同时发生的结果有4种,则P(AB)==,则P(BC)=P(AC)=P(AB),故B正确;事件A、事件B和事件C同时发生的结果有4种,则P(ABC)==,故C错误;因为P(A)P(B)P(C)=××=,故D正确.故选ABD.
三、填空题(本题共4小题,每小题5分,共20分)
13.甲、乙两名运动员各自等可能地从红、白、蓝3种颜色的运动服中选择1种,则他们选择相同颜色运动服的概率为________.
答案
解析 甲、乙两名运动员各自等可能地从红、白、蓝3种颜色的运动服中选择1种的所有可能情况为(红,白),(白,红),(红,蓝),(蓝,红),(白,蓝),(蓝,白),(红,红),(白,白),(蓝,蓝),共9种,这9种情况发生的可能性是相等的.他们选择相同颜色运动服的所有可能情况为(红,红),(白,白),(蓝,蓝),共3种.故所求概率为P==.
14.A,B,C,D四名学生按任意次序站成一排,则A或B在边上的概率为________.
答案
解析 A,B,C,D四名学生按任意次序站成一排,基本事件数共24种,这24种基本事件发生的可能性是相等的,如下图所示.
A,B都不在边上共4种,所以A或B在边上的概率为P=1-=.
15.设两个相互独立的事件A与B,若事件A发生的概率为p,事件B发生的概率为1-p,则A与B同时发生的概率的最大值是________.
答案
解析 A与B同时发生,即事件AB发生,根据相互独立事件的概率的乘法公式,得P(AB)=P(A)P(B)=p(1-p)=p-p2=-2+.当p=时,P(AB)取得最大值.
16.甲、乙两名同学参加一项射击比赛游戏,其中任何一人每射击一次命中目标得2分,未命中目标得0分.若甲、乙两人射击的命中率分别为和p,且甲、乙两人各射击一次得分之和为2的概率为.假设甲、乙两人射击互不影响,则p的值为________,两人各射击一次得分之和不少于2的概率为________.(本题第一空3分,第二空2分)
答案
解析 设“甲射击一次,命中目标”为事件A,“乙射击一次,命中目标”为事件B,则“甲射击一次,未命中目标”为事件,“乙射击一次,未命中目标”为事件,则P(A)=,P()=1-=,P(B)=p,P()=1-p,依题意得×(1-p)+×p=,解得p=.得分之和不少于2的对立事件为得分之和为0,故所求概率为1-×=.
四、解答题(本题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分10分)已知二次函数f(x)=ax2-bx+1,设集合P={1,2,3},Q={-1,1,2,3,4},分别从集合P和Q中随机取1个数,作为a和b,得到数对(a,b).
(1)列举出所有的数对(a,b),并求函数f(x)有零点的概率;
(2)求函数f(x)在区间[1,+∞)上单调递增的概率.
解 (1)(a,b)所有可能的结果为(1,-1),(1,1),(1,2),(1,3),(1,4),(2,-1),(2,1),(2,2),(2,3),(2,4),(3,-1),(3,1),(3,2),(3,3),(3,4),共15种.
若函数f(x)有零点,则b2-4a≥0,有(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),共6种情况满足条件,
所以函数f(x)有零点的概率为=.
(2)函数f(x)的图象的对称轴为直线x=,a>0,
又f(x)在区间[1,+∞)上单调递增,则≤1,有(1,-1),(1,1),(1,2),(2,-1),(2,1),(2,2),(2,3),(2,4),(3,-1),(3,1),(3,2),(3,3),(3,4),共13种情况满足条件,所以函数f(x)在区间[1,+∞)上单调递增的概率为.
18.(本小题满分12分)某中学调查了某班全部45名同学参加书法社团和演讲社团的情况,数据如下表(单位:人):
参加书法社团 未参加书法社团
参加演讲社团 8 5
未参加演讲社团 2 30
(1)从该班随机选1名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的8名同学中,有5名男同学A1,A2,A3,A4,A5,3名女同学B1,B2,B3.现从这5名男同学和3名女同学中各随机选1人,求A1被选中且B1未被选中的概率.
解 (1)记“该同学至少参加上述一个社团”为事件A,则P(A)==.
所以该同学至少参加上述一个社团的概率为.
(2)从5名男同学和3名女同学中各随机选1人的所有的样本点有(A1,B1),(A1,B2),(A1,B3),(A2,B1),(A2,B2),(A2,B3),(A3,B1),(A3,B2),(A3,B3),(A4,B1),(A4,B2),(A4,B3),(A5,B1),(A5,B2),(A5,B3),共15个,这15个样本点发生的可能性是相等的.其中A1被选中且B1未被选中的有(A1,B2),(A1,B3),共2个,所以A1被选中且B1未被选中的概率为P=.
19.(本小题满分12分)某地区有小学21所,中学14所,大学7所,现采用比例分配的分层随机抽样的方法从这些学校中抽取6所学校对学生进行视力调查.
(1)求应从小学、中学、大学中分别抽取的学校数目;
(2)若从抽取的6所学校中随机抽取2所学校做进一步数据分析:
①列出所有可能的抽取结果;
②求抽取的2所学校均为小学的概率.
解 (1)从小学中抽取的学校数目为6×=3,从中学中抽取的学校数目为6×=2,从大学中抽取的学校数目为6×=1.
(2)①在抽取到的6所学校中,3所小学分别记为A1,A2,A3,2所中学分别记为A4,A5,大学记为A6,则抽取2所学校的所有可能结果为(A1,A2),(A1,A3),(A1,A4),(A1,A5),(A1,A6),(A2,A3),(A2,A4),(A2,A5),(A2,A6),(A3,A4),(A3,A5),(A3,A6),(A4,A5),(A4,A6),(A5,A6),共15种,每种结果出现的可能性相等.
②从6所学校中抽取的2所学校均为小学(记为事件B)的所有可能结果为(A1,A2),(A1,A3),(A2,A3),共3种.
所以P(B)==.
所以抽取的2所学校均为小学的概率为.
20.(本小题满分12分)袋子中放有大小和形状相同的小球若干个,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个.已知从袋子中随机抽取1个小球,取到标号是2的小球的概率是.
(1)求n的值;
(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为a,第二次取出的小球标号为b.记事件A表示“a+b=2”,求事件A的概率.
解 (1)由题意可知,取到标号为2的小球的概率为,可得=,解得n=2.
(2)不放回地随机抽取2个小球的所有样本点为:(0,1),(0,21),(0,22),(1,0),(1,21),(1,22),(21,0),(21,1),(21,22),(22,0),(22,1),(22,21),共12个,这12个样本点发生的可能性是相等的.事件A包含的样本点为(0,21),(0,22),(21,0),(22,0),共4个.所以P(A)==.
21.(本小题满分12分)在某次1500米体能测试中,甲、乙、丙三人各自通过测试的概率分别为,,,求:
(1)3人都通过体能测试的概率;
(2)只有2人通过体能测试的概率;
(3)只有1人通过体能测试的概率.
解 设事件A表示“甲通过体能测试”,事件B表示“乙通过体能测试”,事件C表示“丙通过体能测试”.由题意有:
P(A)=,P(B)=,P(C)=.
(1)设M1表示事件“甲、乙、丙3人都通过体能测试”,即M1=ABC.
由事件A,B,C相互独立,可得
P(M1)=P(ABC)=P(A)P(B)P(C)=××=.
所以3人都通过体能测试的概率为.
(2)设M2表示事件“甲、乙、丙3人中只有2人通过体能测试”,则M2=AB∪AC∪BC,由于事件A,B,C,,,均相互独立,并且事件AB,AC,BC两两互斥,因此所求概率为
P(M2)=P(A)P(B)P()+P(A)P()P(C)+P()P(B)P(C)=××+××+××=.
所以只有2人通过体能测试的概率为.
(3)设M3表示事件“甲、乙、丙3人中只有1人通过体能测试”,则M3=A ∪B∪ C,
由于事件A,B,C,,,均相互独立,并且事件A ,B, C两两互斥,因此所求概率为P(M3)=P(A)P()P()+P()P(B)P()+P()P()P(C)=××+××+××=.
所以只有1人通过体能测试的概率为.
22.(本小题满分12分)某中学作为蓝色海洋教育特色学校,随机抽取100名学生,进行一次海洋知识测试,按测试成绩(假设考试成绩均在[65,90)内)分组如下:第一组[65,70),第二组[70,75),第三组[75,80),第四组[80,85),第五组[85,90),得到频率分布直方图如图.
(1)求测试成绩在[80,85)内的频率;
(2)从第三、四、五组学生中用比例分配的分层随机抽样的方法抽取6名学生组成海洋知识宣讲小组,定期在校内进行义务宣讲,并在这6名学生中随机选取2名参加市组织的蓝色海洋教育义务宣讲队,求第四组至少有1名学生被抽中的概率.
解 (1)测试成绩在[80,85)内的频率为1-(0.01+0.07+0.06+0.02)×5=0.2.
(2)第三组的人数为0.06×5×100=30,第四组的人数为0.2×100=20,第五组的人数为0.02×5×100=10,所以第三组抽取3人,第四组抽取2人,第五组抽取1人.
设第三组抽到的3人为A1,A2,A3,第四组抽到的2人为B1,B2,第五组抽到的1人为C.
从6名学生中随机选取2名学生的所有可能结果有15种:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C),(A2,A3),(A2,B1),(A2,B2),(A2,C),(A3,B1),(A3,B2),(A3,C),(B1,B2),(B1,C),(B2,C),这15种结果出现的可能性相等.
设“第四组2名学生中至少有1名学生被抽中”为事件M,则事件M包含的样本点有(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),(B1,C),(B2,C),共9种.
所以第四组至少有1名学生被抽中的概率P(M)==.
时间:120分钟 满分:150分
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若“A∪B”发生(A,B中至少有一个发生)的概率为0.6,则,同时发生的概率为( )
A.0.6 B.0.36 C.0.24 D.0.4
2.若干个人站成一排,其中为互斥事件的是( )
A.“甲站排头”与“乙站排头”
B.“甲站排头”与“乙不站排尾”
C.“甲站排头”与“乙站排尾”
D.“甲不站排头”与“乙不站排尾”
3.口袋内装有一些大小相同的红球、白球和黑球,从中摸出1个球,摸出红球的概率是0.52,摸出白球的概率是0.28,那么摸出黑球的概率是( )
A.0.2 B.0.28 C.0.52 D.0.8
4.在5盒酸奶中,有2盒已经过了保质期,从中任取2盒,取到的酸奶中有已过保质期的概率为( )
A. B. C. D.
5.从2名男生和2名女生中任意选择两人在星期六、星期日参加某公益活动,每天一人,则星期六安排一名男生、星期日安排一名女生的概率为( )
A. B. C. D.
6.已知A={1,2,3},B={x∈R|x2-ax+b=0,a∈A,b∈A},则事件“A∩B=B”发生的概率是( )
A. B. C. D.1
7.某公司共有职工8000名,从中随机抽取了100名,调查上、下班乘车所用时间,得下表:
所用时间(分钟) [0,20) [20,40) [40,60) [60,80) [80,100]
人数 25 50 15 5 5
公司规定,按照乘车所用时间每月发给职工路途补贴,补贴金额y(元)与乘车时间t(分钟)的关系是y=200+40,其中表示不超过的最大整数.以样本频率为概率,则公司一名职工每月用于路途补贴不超过300元的概率为( )
A.0.5 B.0.7 C.0.8 D.0.9
8.为了调查某厂2000名工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35],频率分布直方图如图所示.工厂规定从生产低于20件产品的工人中随机地选取2位工人进行培训,则这2位工人不在同一组的概率是( )
A. B. C. D.
二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分)
9.下列事件中,是随机事件的是( )
A.2022年8月18日,北京市不下雨
B.在标准大气压下,水在4 ℃时结冰
C.从标有1,2,3,4的4张号签中任取一张,恰为1号签
D.x∈R,则|x|的值不小于0
10.袋中有大小相同的黄、红、白球各一个,每次任取一个,有放回地取3次,则下列说法正确的是( )
A.取出的3个球颜色相同的概率为
B.取出的3个球颜色不全相同的概率为
C.取出的3个球颜色全不相同的概率为
D.取出的3个球无红球的概率为
11.某年级有12个班,现要从2班到12班中选1个班的学生参加一项活动,有人提议:掷两个骰子,得到的点数之和是几就选几班,这种选法( )
A.公平,每个班被选到的概率都为
B.不公平,6班被选到的概率最大
C.不公平,2班和12班被选到的概率最小
D.不公平,7班被选到的概率最大
12.甲、乙两个质地均匀且完全一样的四面体,每个面都是正三角形,甲四个面上分别标有数字1,2,3,4,乙四个面上分别标有数字5,6,7,8,同时抛掷这两个四面体一次,记事件A为“两个四面体朝下一面的数字之和为奇数”,事件B为“甲四面体朝下一面的数字为奇数”,事件C为“乙四面体朝下一面的数字为偶数”,则下列结论正确的是( )
A.P(A)=P(B)=P(C)
B.P(BC)=P(AC)=P(AB)
C.P(ABC)=
D.P(A)P(B)P(C)=
三、填空题(本题共4小题,每小题5分,共20分)
13.甲、乙两名运动员各自等可能地从红、白、蓝3种颜色的运动服中选择1种,则他们选择相同颜色运动服的概率为________.
14.A,B,C,D四名学生按任意次序站成一排,则A或B在边上的概率为________.
15.设两个相互独立的事件A与B,若事件A发生的概率为p,事件B发生的概率为1-p,则A与B同时发生的概率的最大值是________.
16.甲、乙两名同学参加一项射击比赛游戏,其中任何一人每射击一次命中目标得2分,未命中目标得0分.若甲、乙两人射击的命中率分别为和p,且甲、乙两人各射击一次得分之和为2的概率为.假设甲、乙两人射击互不影响,则p的值为________,两人各射击一次得分之和不少于2的概率为________.(本题第一空3分,第二空2分)
四、解答题(本题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分10分)已知二次函数f(x)=ax2-bx+1,设集合P={1,2,3},Q={-1,1,2,3,4},分别从集合P和Q中随机取1个数,作为a和b,得到数对(a,b).
(1)列举出所有的数对(a,b),并求函数f(x)有零点的概率;
(2)求函数f(x)在区间[1,+∞)上单调递增的概率.
18.(本小题满分12分)某中学调查了某班全部45名同学参加书法社团和演讲社团的情况,数据如下表(单位:人):
参加书法社团 未参加书法社团
参加演讲社团 8 5
未参加演讲社团 2 30
(1)从该班随机选1名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的8名同学中,有5名男同学A1,A2,A3,A4,A5,3名女同学B1,B2,B3.现从这5名男同学和3名女同学中各随机选1人,求A1被选中且B1未被选中的概率.
19.(本小题满分12分)某地区有小学21所,中学14所,大学7所,现采用比例分配的分层随机抽样的方法从这些学校中抽取6所学校对学生进行视力调查.
(1)求应从小学、中学、大学中分别抽取的学校数目;
(2)若从抽取的6所学校中随机抽取2所学校做进一步数据分析:
①列出所有可能的抽取结果;
②求抽取的2所学校均为小学的概率.
20.(本小题满分12分)袋子中放有大小和形状相同的小球若干个,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个.已知从袋子中随机抽取1个小球,取到标号是2的小球的概率是.
(1)求n的值;
(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为a,第二次取出的小球标号为b.记事件A表示“a+b=2”,求事件A的概率.
21.(本小题满分12分)在某次1500米体能测试中,甲、乙、丙三人各自通过测试的概率分别为,,,求:
(1)3人都通过体能测试的概率;
(2)只有2人通过体能测试的概率;
(3)只有1人通过体能测试的概率.
22.(本小题满分12分)某中学作为蓝色海洋教育特色学校,随机抽取100名学生,进行一次海洋知识测试,按测试成绩(假设考试成绩均在[65,90)内)分组如下:第一组[65,70),第二组[70,75),第三组[75,80),第四组[80,85),第五组[85,90),得到频率分布直方图如图.
(1)求测试成绩在[80,85)内的频率;
(2)从第三、四、五组学生中用比例分配的分层随机抽样的方法抽取6名学生组成海洋知识宣讲小组,定期在校内进行义务宣讲,并在这6名学生中随机选取2名参加市组织的蓝色海洋教育义务宣讲队,求第四组至少有1名学生被抽中的概率.
第十章 单元质量测评
时间:120分钟 满分:150分
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若“A∪B”发生(A,B中至少有一个发生)的概率为0.6,则,同时发生的概率为( )
A.0.6 B.0.36 C.0.24 D.0.4
答案 D
解析 “A∪B”发生指A,B中至少有一个发生,它的对立事件为A,B都不发生,即,同时发生.
2.若干个人站成一排,其中为互斥事件的是( )
A.“甲站排头”与“乙站排头”
B.“甲站排头”与“乙不站排尾”
C.“甲站排头”与“乙站排尾”
D.“甲不站排头”与“乙不站排尾”
答案 A
解析 由互斥事件的定义可得,“甲站排头”与“乙站排头”为互斥事件.
3.口袋内装有一些大小相同的红球、白球和黑球,从中摸出1个球,摸出红球的概率是0.52,摸出白球的概率是0.28,那么摸出黑球的概率是( )
A.0.2 B.0.28 C.0.52 D.0.8
答案 A
解析 设“摸出红球”为事件M,“摸出白球”为事件N,“摸出黑球”为事件E,则P(M)+P(N)+P(E)=1,所以P(E)=1-P(M)-P(N)=1-0.52-0.28=0.2.故选A.
4.在5盒酸奶中,有2盒已经过了保质期,从中任取2盒,取到的酸奶中有已过保质期的概率为( )
A. B. C. D.
答案 C
解析 对5盒酸奶编号1~5,4,5代表过期.从中任取2盒,则样本点有(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5),共10个,这10个样本点出现的可能性相等.含4,5的有7个,所以所求概率为,故选C.
5.从2名男生和2名女生中任意选择两人在星期六、星期日参加某公益活动,每天一人,则星期六安排一名男生、星期日安排一名女生的概率为( )
A. B. C. D.
答案 A
解析 设2名男生记为A1,A2,2名女生记为B1,B2,任意选择两人在星期六、星期日参加某公益活动,有A1A2,A1B1,A1B2,A2B1,A2B2,B1B2,A2A1,B1A1,B2A1,B1A2,B2A2,B2B1,共12种情况,这12种情况发生的可能性是相等的.而星期六安排一名男生、星期日安排一名女生有A1B1,A1B2,A2B1,A2B2,共4种情况,则所求事件发生的概率为P==.故选A.
6.已知A={1,2,3},B={x∈R|x2-ax+b=0,a∈A,b∈A},则事件“A∩B=B”发生的概率是( )
A. B. C. D.1
答案 C
解析 ∵A∩B=B,∴B可能为?,{1},{2},{3},{1,2},{2,3},{1,3}.当B=?时,a2-4b<0,满足条件的a,b为a=1,b=1,2,3;a=2,b=2,3;a=3,b=3.当B={1}时,满足条件的a,b为a=2,b=1.当B={2},{3}时,没有满足条件的a,b.当B={1,2}时,满足条件的a,b为a=3,b=2.当B={2,3},{1,3}时,没有满足条件的a,b,∴事件“A∩B=B”发生的概率为=.故选C.
7.某公司共有职工8000名,从中随机抽取了100名,调查上、下班乘车所用时间,得下表:
所用时间(分钟) [0,20) [20,40) [40,60) [60,80) [80,100]
人数 25 50 15 5 5
公司规定,按照乘车所用时间每月发给职工路途补贴,补贴金额y(元)与乘车时间t(分钟)的关系是y=200+40,其中表示不超过的最大整数.以样本频率为概率,则公司一名职工每月用于路途补贴不超过300元的概率为( )
A.0.5 B.0.7 C.0.8 D.0.9
答案 D
解析 由题意知y≤300,即200+40≤300,即≤2.5,解得0≤t<60,由表可知t∈[0,60)的人数为90,故所求概率为=0.9.
8.为了调查某厂2000名工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35],频率分布直方图如图所示.工厂规定从生产低于20件产品的工人中随机地选取2位工人进行培训,则这2位工人不在同一组的概率是( )
A. B. C. D.
答案 C
解析 根据题中频率分布直方图可知产品件数在[10,15),[15,20)内的人数分别为5×0.02×20=2,5×0.04×20=4,
设生产产品件数在[10,15)内的2人分别是A,B,
设生产产品件数在[15,20)内的4人分别是C,D,E,F,
则从生产低于20件产品的工人中随机地选取2位工人的结果有(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共15种,这15种结果出现的可能性相等.
2位工人不在同一组的结果有(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),共8种.
则选取的这2人不在同一组的概率为.
二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分)
9.下列事件中,是随机事件的是( )
A.2022年8月18日,北京市不下雨
B.在标准大气压下,水在4 ℃时结冰
C.从标有1,2,3,4的4张号签中任取一张,恰为1号签
D.x∈R,则|x|的值不小于0
答案 AC
解析 A,C为随机事件,B为不可能事件,D为必然事件.
10.袋中有大小相同的黄、红、白球各一个,每次任取一个,有放回地取3次,则下列说法正确的是( )
A.取出的3个球颜色相同的概率为
B.取出的3个球颜色不全相同的概率为
C.取出的3个球颜色全不相同的概率为
D.取出的3个球无红球的概率为
答案 BC
解析 有放回地取球3次,共27种可能结果,其中颜色相同的结果有3种,其概率为=,故A错误;颜色不全相同的结果有24种,其概率为=,故B正确;颜色全不相同的结果有6种,其概率为=,故C正确;无红球的结果有8种,其概率为,故D错误.故选BC.
11.某年级有12个班,现要从2班到12班中选1个班的学生参加一项活动,有人提议:掷两个骰子,得到的点数之和是几就选几班,这种选法( )
A.公平,每个班被选到的概率都为
B.不公平,6班被选到的概率最大
C.不公平,2班和12班被选到的概率最小
D.不公平,7班被选到的概率最大
答案 CD
解析 设i班被选到的概率为P(i),i=2,3,4,…,12,则P(2)=P(12)=,P(3)=P(11)=,P(4)=P(10)=,P(5)=P(9)=,P(6)=P(8)=,P(7)=,故选CD.
12.甲、乙两个质地均匀且完全一样的四面体,每个面都是正三角形,甲四个面上分别标有数字1,2,3,4,乙四个面上分别标有数字5,6,7,8,同时抛掷这两个四面体一次,记事件A为“两个四面体朝下一面的数字之和为奇数”,事件B为“甲四面体朝下一面的数字为奇数”,事件C为“乙四面体朝下一面的数字为偶数”,则下列结论正确的是( )
A.P(A)=P(B)=P(C)
B.P(BC)=P(AC)=P(AB)
C.P(ABC)=
D.P(A)P(B)P(C)=
答案 ABD
解析 记(x,y)中的x表示甲四面体朝下一面的数字,y表示乙四面体朝下一面的数字,则所有可能出现的结果为(1,5),(1,6),(1,7),(1,8),(2,5),(2,6),(2,7),(2,8),(3,5),(3,6),(3,7),(3,8),(4,5),(4,6),(4,7),(4,8),共16种,且每种结果出现的可能性相等.满足事件A的结果有8种,则P(A)==,满足事件B的结果有8种,则P(B)==,满足事件C的结果有8种,则P(C)==,则P(A)=P(B)=P(C),故A正确;事件B和事件C同时发生的结果有4种,则P(BC)==,事件A和事件C同时发生的结果有4种,则P(AC)==,事件A和事件B同时发生的结果有4种,则P(AB)==,则P(BC)=P(AC)=P(AB),故B正确;事件A、事件B和事件C同时发生的结果有4种,则P(ABC)==,故C错误;因为P(A)P(B)P(C)=××=,故D正确.故选ABD.
三、填空题(本题共4小题,每小题5分,共20分)
13.甲、乙两名运动员各自等可能地从红、白、蓝3种颜色的运动服中选择1种,则他们选择相同颜色运动服的概率为________.
答案
解析 甲、乙两名运动员各自等可能地从红、白、蓝3种颜色的运动服中选择1种的所有可能情况为(红,白),(白,红),(红,蓝),(蓝,红),(白,蓝),(蓝,白),(红,红),(白,白),(蓝,蓝),共9种,这9种情况发生的可能性是相等的.他们选择相同颜色运动服的所有可能情况为(红,红),(白,白),(蓝,蓝),共3种.故所求概率为P==.
14.A,B,C,D四名学生按任意次序站成一排,则A或B在边上的概率为________.
答案
解析 A,B,C,D四名学生按任意次序站成一排,基本事件数共24种,这24种基本事件发生的可能性是相等的,如下图所示.
A,B都不在边上共4种,所以A或B在边上的概率为P=1-=.
15.设两个相互独立的事件A与B,若事件A发生的概率为p,事件B发生的概率为1-p,则A与B同时发生的概率的最大值是________.
答案
解析 A与B同时发生,即事件AB发生,根据相互独立事件的概率的乘法公式,得P(AB)=P(A)P(B)=p(1-p)=p-p2=-2+.当p=时,P(AB)取得最大值.
16.甲、乙两名同学参加一项射击比赛游戏,其中任何一人每射击一次命中目标得2分,未命中目标得0分.若甲、乙两人射击的命中率分别为和p,且甲、乙两人各射击一次得分之和为2的概率为.假设甲、乙两人射击互不影响,则p的值为________,两人各射击一次得分之和不少于2的概率为________.(本题第一空3分,第二空2分)
答案
解析 设“甲射击一次,命中目标”为事件A,“乙射击一次,命中目标”为事件B,则“甲射击一次,未命中目标”为事件,“乙射击一次,未命中目标”为事件,则P(A)=,P()=1-=,P(B)=p,P()=1-p,依题意得×(1-p)+×p=,解得p=.得分之和不少于2的对立事件为得分之和为0,故所求概率为1-×=.
四、解答题(本题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分10分)已知二次函数f(x)=ax2-bx+1,设集合P={1,2,3},Q={-1,1,2,3,4},分别从集合P和Q中随机取1个数,作为a和b,得到数对(a,b).
(1)列举出所有的数对(a,b),并求函数f(x)有零点的概率;
(2)求函数f(x)在区间[1,+∞)上单调递增的概率.
解 (1)(a,b)所有可能的结果为(1,-1),(1,1),(1,2),(1,3),(1,4),(2,-1),(2,1),(2,2),(2,3),(2,4),(3,-1),(3,1),(3,2),(3,3),(3,4),共15种.
若函数f(x)有零点,则b2-4a≥0,有(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),共6种情况满足条件,
所以函数f(x)有零点的概率为=.
(2)函数f(x)的图象的对称轴为直线x=,a>0,
又f(x)在区间[1,+∞)上单调递增,则≤1,有(1,-1),(1,1),(1,2),(2,-1),(2,1),(2,2),(2,3),(2,4),(3,-1),(3,1),(3,2),(3,3),(3,4),共13种情况满足条件,所以函数f(x)在区间[1,+∞)上单调递增的概率为.
18.(本小题满分12分)某中学调查了某班全部45名同学参加书法社团和演讲社团的情况,数据如下表(单位:人):
参加书法社团 未参加书法社团
参加演讲社团 8 5
未参加演讲社团 2 30
(1)从该班随机选1名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的8名同学中,有5名男同学A1,A2,A3,A4,A5,3名女同学B1,B2,B3.现从这5名男同学和3名女同学中各随机选1人,求A1被选中且B1未被选中的概率.
解 (1)记“该同学至少参加上述一个社团”为事件A,则P(A)==.
所以该同学至少参加上述一个社团的概率为.
(2)从5名男同学和3名女同学中各随机选1人的所有的样本点有(A1,B1),(A1,B2),(A1,B3),(A2,B1),(A2,B2),(A2,B3),(A3,B1),(A3,B2),(A3,B3),(A4,B1),(A4,B2),(A4,B3),(A5,B1),(A5,B2),(A5,B3),共15个,这15个样本点发生的可能性是相等的.其中A1被选中且B1未被选中的有(A1,B2),(A1,B3),共2个,所以A1被选中且B1未被选中的概率为P=.
19.(本小题满分12分)某地区有小学21所,中学14所,大学7所,现采用比例分配的分层随机抽样的方法从这些学校中抽取6所学校对学生进行视力调查.
(1)求应从小学、中学、大学中分别抽取的学校数目;
(2)若从抽取的6所学校中随机抽取2所学校做进一步数据分析:
①列出所有可能的抽取结果;
②求抽取的2所学校均为小学的概率.
解 (1)从小学中抽取的学校数目为6×=3,从中学中抽取的学校数目为6×=2,从大学中抽取的学校数目为6×=1.
(2)①在抽取到的6所学校中,3所小学分别记为A1,A2,A3,2所中学分别记为A4,A5,大学记为A6,则抽取2所学校的所有可能结果为(A1,A2),(A1,A3),(A1,A4),(A1,A5),(A1,A6),(A2,A3),(A2,A4),(A2,A5),(A2,A6),(A3,A4),(A3,A5),(A3,A6),(A4,A5),(A4,A6),(A5,A6),共15种,每种结果出现的可能性相等.
②从6所学校中抽取的2所学校均为小学(记为事件B)的所有可能结果为(A1,A2),(A1,A3),(A2,A3),共3种.
所以P(B)==.
所以抽取的2所学校均为小学的概率为.
20.(本小题满分12分)袋子中放有大小和形状相同的小球若干个,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个.已知从袋子中随机抽取1个小球,取到标号是2的小球的概率是.
(1)求n的值;
(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为a,第二次取出的小球标号为b.记事件A表示“a+b=2”,求事件A的概率.
解 (1)由题意可知,取到标号为2的小球的概率为,可得=,解得n=2.
(2)不放回地随机抽取2个小球的所有样本点为:(0,1),(0,21),(0,22),(1,0),(1,21),(1,22),(21,0),(21,1),(21,22),(22,0),(22,1),(22,21),共12个,这12个样本点发生的可能性是相等的.事件A包含的样本点为(0,21),(0,22),(21,0),(22,0),共4个.所以P(A)==.
21.(本小题满分12分)在某次1500米体能测试中,甲、乙、丙三人各自通过测试的概率分别为,,,求:
(1)3人都通过体能测试的概率;
(2)只有2人通过体能测试的概率;
(3)只有1人通过体能测试的概率.
解 设事件A表示“甲通过体能测试”,事件B表示“乙通过体能测试”,事件C表示“丙通过体能测试”.由题意有:
P(A)=,P(B)=,P(C)=.
(1)设M1表示事件“甲、乙、丙3人都通过体能测试”,即M1=ABC.
由事件A,B,C相互独立,可得
P(M1)=P(ABC)=P(A)P(B)P(C)=××=.
所以3人都通过体能测试的概率为.
(2)设M2表示事件“甲、乙、丙3人中只有2人通过体能测试”,则M2=AB∪AC∪BC,由于事件A,B,C,,,均相互独立,并且事件AB,AC,BC两两互斥,因此所求概率为
P(M2)=P(A)P(B)P()+P(A)P()P(C)+P()P(B)P(C)=××+××+××=.
所以只有2人通过体能测试的概率为.
(3)设M3表示事件“甲、乙、丙3人中只有1人通过体能测试”,则M3=A ∪B∪ C,
由于事件A,B,C,,,均相互独立,并且事件A ,B, C两两互斥,因此所求概率为P(M3)=P(A)P()P()+P()P(B)P()+P()P()P(C)=××+××+××=.
所以只有1人通过体能测试的概率为.
22.(本小题满分12分)某中学作为蓝色海洋教育特色学校,随机抽取100名学生,进行一次海洋知识测试,按测试成绩(假设考试成绩均在[65,90)内)分组如下:第一组[65,70),第二组[70,75),第三组[75,80),第四组[80,85),第五组[85,90),得到频率分布直方图如图.
(1)求测试成绩在[80,85)内的频率;
(2)从第三、四、五组学生中用比例分配的分层随机抽样的方法抽取6名学生组成海洋知识宣讲小组,定期在校内进行义务宣讲,并在这6名学生中随机选取2名参加市组织的蓝色海洋教育义务宣讲队,求第四组至少有1名学生被抽中的概率.
解 (1)测试成绩在[80,85)内的频率为1-(0.01+0.07+0.06+0.02)×5=0.2.
(2)第三组的人数为0.06×5×100=30,第四组的人数为0.2×100=20,第五组的人数为0.02×5×100=10,所以第三组抽取3人,第四组抽取2人,第五组抽取1人.
设第三组抽到的3人为A1,A2,A3,第四组抽到的2人为B1,B2,第五组抽到的1人为C.
从6名学生中随机选取2名学生的所有可能结果有15种:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C),(A2,A3),(A2,B1),(A2,B2),(A2,C),(A3,B1),(A3,B2),(A3,C),(B1,B2),(B1,C),(B2,C),这15种结果出现的可能性相等.
设“第四组2名学生中至少有1名学生被抽中”为事件M,则事件M包含的样本点有(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),(B1,C),(B2,C),共9种.
所以第四组至少有1名学生被抽中的概率P(M)==.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
