第二章统计章末训练卷 (含解析)2020-2021学年高一下学期数学人教A版必修3
文档属性
| 名称 | 第二章统计章末训练卷 (含解析)2020-2021学年高一下学期数学人教A版必修3 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 00:00:00 | ||
图片预览


文档简介
人教A版必修3第二章章末训练卷
统计
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.问题:①某社区有500个家庭,其中高收入家庭125户,中等收入家庭280户,低收入家庭95户,为了了解社会购买力的某项指标,要从中抽出一个容量为100户的样本;②从10名学生中抽出3人参加座谈会,方法:Ⅰ简单随机抽样法;Ⅱ分层抽样法.则问题与方法配对正确的是( )
A.①Ⅰ②Ⅱ B.①Ⅰ②Ⅰ C.①Ⅱ②Ⅰ D.①Ⅱ②Ⅱ
2.某工厂利用随机数表对生产的700个零件进行抽样测试,先将700个零件进行编号,001,002,…,699,700,从中抽取70个样本,下图提供随机数表的第4行到第6行,若从表中第5行第6列开始向右读取数据,则得到的第8个样本编号是( )
A.623 B.368 C.253 D.072
3.设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,,n),用最小二乘法建立的回归方程为.
①y与x具有正的线性相关关系;
②回归直线过样本点的中心;
③若该大学某女生身高增加1cm,则其体重约增加;
④若该大学某女生身高为170cm,则其体重必为.
则上述判断不正确的个数是( )
A.1 B.2 C.3 D.4
4.“脱口秀大赛”上选手的分数分为观众评分和嘉宾评分.组织方将观众评分按照,,分组,绘制频率分布直方图如图所示.嘉宾评分的平均数为,观众评分的平均数为,中位数为,则下列选项正确的是( )
嘉宾
评分 96 97 96 89 97 98
A. B.
C. D.
5.若样本数据,,…,的标准差为,则数据,,…,的标准差为( )
A. B. C. D.
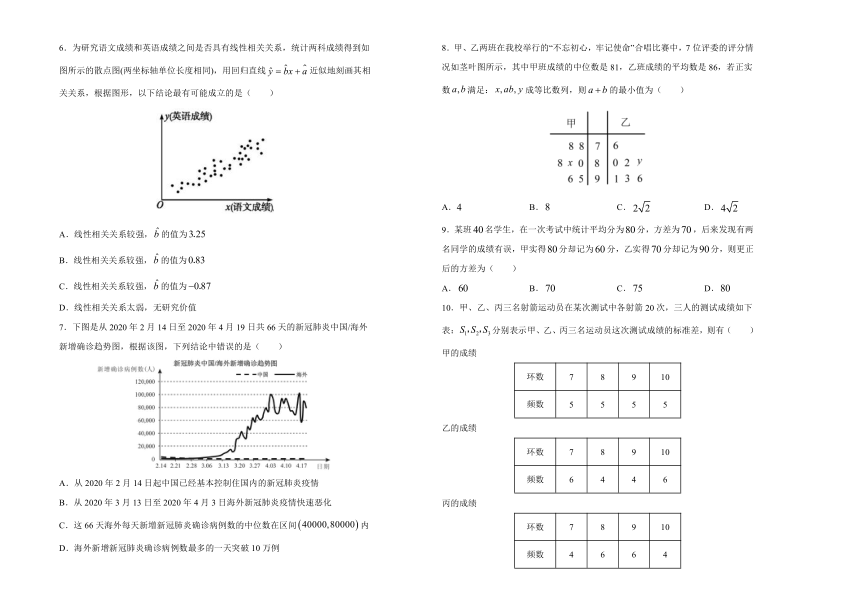
6.为研究语文成绩和英语成绩之间是否具有线性相关关系,统计两科成绩得到如图所示的散点图(两坐标轴单位长度相同),用回归直线近似地刻画其相关关系,根据图形,以下结论最有可能成立的是( )
A.线性相关关系较强,的值为
B.线性相关关系较强,的值为
C.线性相关关系较强,的值为
D.线性相关关系太弱,无研究价值
7.下图是从2020年2月14日至2020年4月19日共66天的新冠肺炎中国/海外新增确诊趋势图,根据该图,下列结论中错误的是( )
A.从2020年2月14日起中国已经基本控制住国内的新冠肺炎疫情
B.从2020年3月13日至2020年4月3日海外新冠肺炎疫情快速恶化
C.这66天海外每天新增新冠肺炎确诊病例数的中位数在区间内
D.海外新增新冠肺炎确诊病例数最多的一天突破10万例
8.甲、乙两班在我校举行的“不忘初心,牢记使命”合唱比赛中,7位评委的评分情况如茎叶图所示,其中甲班成绩的中位数是81,乙班成绩的平均数是86,若正实数满足:成等比数列,则的最小值为( )
A.4 B. C. D.
9.某班名学生,在一次考试中统计平均分为分,方差为,后来发现有两名同学的成绩有误,甲实得分却记为分,乙实得分却记为分,则更正后的方差为( )
A. B. C. D.
10.甲、乙、丙三名射箭运动员在某次测试中各射箭20次,三人的测试成绩如下表:分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有( )
甲的成绩
环数 7 8 9 10
频数 5 5 5 5
乙的成绩
环数 7 8 9 10
频数 6 4 4 6
丙的成绩
环数 7 8 9 10
频数 4 6 6 4
A. B.
C. D.
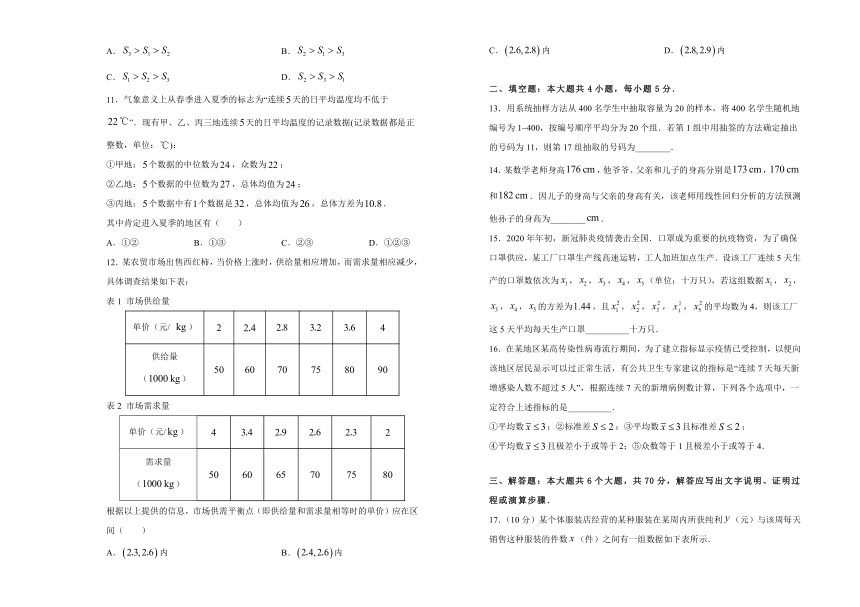
11.气象意义上从春季进入夏季的标志为“连续天的日平均温度均不低于”.现有甲、乙、丙三地连续天的日平均温度的记录数据(记录数据都是正整数,单位:):
①甲地:个数据的中位数为,众数为;
②乙地:个数据的中位数为,总体均值为;
③丙地:个数据中有个数据是,总体均值为,总体方差为.
其中肯定进入夏季的地区有( )
A.①② B.①③ C.②③ D.①②③
12.某农贸市场出售西红柿,当价格上涨时,供给量相应增加,而需求量相应减少,具体调查结果如下表:
表1 市场供给量
单价(元/ ) 2
4
供给量() 50 60 70 75 80 90
表2 市场需求量
单价(元/) 4
2
需求量() 50 60 65 70 75 80
根据以上提供的信息,市场供需平衡点(即供给量和需求量相等时的单价)应在区间( )
A.内 B.内
C.内 D.内
二、填空题:本大题共4小题,每小题5分.
13.用系统抽样方法从400名学生中抽取容量为20的样本,将400名学生随机地编号为1~400,按编号顺序平均分为20个组.若第1组中用抽签的方法确定抽出的号码为11,则第17组抽取的号码为________.
14.某数学老师身高,他爷爷、父亲和儿子的身高分别是,和.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为________.
15.2020年年初,新冠肺炎疫情袭击全国.口罩成为重要的抗疫物资,为了确保口罩供应,某工厂口罩生产线高速运转,工人加班加点生产.设该工厂连续5天生产的口罩数依次为,,,,(单位:十万只),若这组数据,,,,的方差为,且,,,,的平均数为4,则该工厂这5天平均每天生产口罩__________十万只.
16.在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各个选项中,一定符合上述指标的是__________.
①平均数;②标准差;③平均数且标准差;
④平均数且极差小于或等于2;⑤众数等于1且极差小于或等于4.
三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
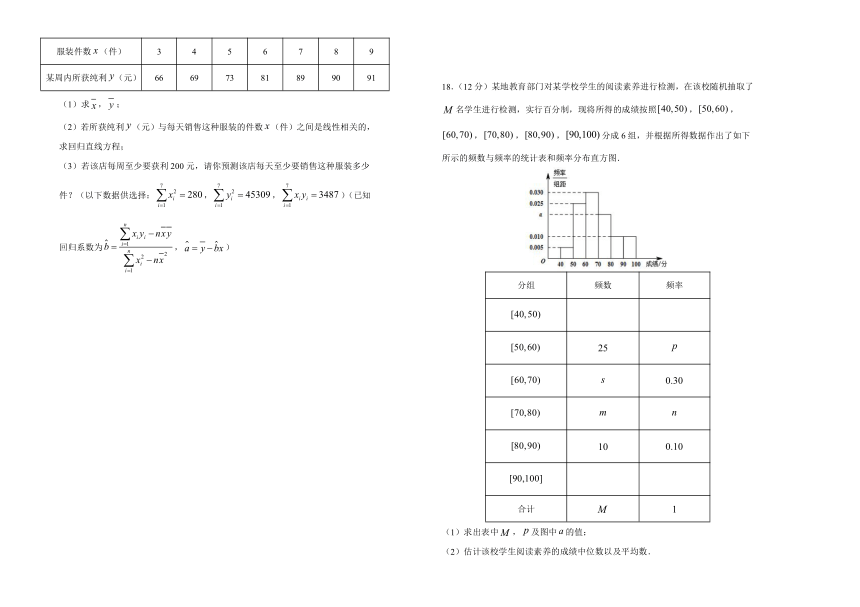
17.(10分)某个体服装店经营的某种服装在某周内所获纯利(元)与该周每天销售这种服装的件数(件)之间有一组数据如下表所示.
服装件数(件) 3 4 5 6 7 8 9
某周内所获纯利(元) 66 69 73 81 89 90 91
(1)求,;
(2)若所获纯利(元)与每天销售这种服装的件数(件)之间是线性相关的,求回归直线方程;
(3)若该店每周至少要获利200元,请你预测该店每天至少要销售这种服装多少件?(以下数据供选择:,,)(已知回归系数为,)
18.(12分)某地教育部门对某学校学生的阅读素养进行检测,在该校随机抽取了名学生进行检测,实行百分制,现将所得的成绩按照,,,,,分成6组,并根据所得数据作出了如下所示的频数与频率的统计表和频率分布直方图.
分组 频数 频率
25
10
合计
1
(1)求出表中,及图中的值;
(2)估计该校学生阅读素养的成绩中位数以及平均数.
19.(12分)一家保险公司决定对推销员实行月标管理,按以往月销售额(单位:千元)把推销员分为甲、乙、丙三个层次,各层次人数如下:
甲 乙 丙
月销售额
人数 120 240 90
(1)为了了解推销员对目标设定的意见,决定从甲、乙、丙三个层次中采取比例分配的分层随机抽样抽取30人进行座谈,请计算甲、乙、丙三个层次各应抽取多少人?
(2)确定销售日标是否合适,直接影响到公司的经济效益,如果目标定得过高,多数推销员完不成任务,会使推销员失去信心;如果目标定得太低,将不利于挖掘推销员的工作潜力.现已知按上面的方法抽取了部分推销员的月销售额(单位:千元):
公司为了使70%的推销员能够完成销售目标,根据这组样本数据,应将销售目标定为多少比较合理?
20.(12分)为了了解某工厂生产的产品情况,从该工厂生产的产品随机抽取了一个容量为200的样本,测量它们的尺寸(单位:),数据分为,,,,,,七组,其频率分布直方图如图所示.
(1)根据频率分布直方图,求200件样本中尺寸在内的样本数;
(2)记产品尺寸在内为等品,每件可获利6元;产品尺寸在内为不合格品,每件亏损3元;其余的为合格品,每件可获利4元.若该机器一个月共生产2000件产品.以样本的频率代替总体在各组的频率,若单月利润未能达到9000元,则需要对该工厂设备实施升级改造.试判断是否需要对该工厂设备实施升级改造.
21.(12分)6月17日是联合国确定的“世界防治荒漠化和干旱日”,为增强全社会对防治荒漠化的认识与关注,聚焦联合国2030可持续发展目标——实现全球土地退化零增长.自2004年以来,我国荒漠化和沙化状况呈现整体遏制、持续缩减、功能增强、成效明显的良好态势.治理沙漠离不开优质的树苗,现从苗圃中随机地抽测了200株树苗的高度(单位:cm),得到以下频率分布直方图.
(1)求直方图中的值及众数、中位数;
(2)若树高185cm及以上是可以移栽的合格树苗.
①求合格树苗的平均高度(结果精确到个位);
②从样本中按分层抽样方法抽取20株树苗作进一步研究,不合格树苗、合格树苗分别应抽取多少株?
22.(12分)在一次抽样调查中测得个样本点,得到下表及散点图.
(1)根据散点图判断与,哪一个适宜作为关于的回归方程;(给出判断即可,不必说明理由)
(2)根据(1)的判断结果试建立与的回归方程;(计算结果保留整数)
(3)在(2)的条件下,设且,试求的最小值.
参考公式:回归方程中,,.
人教A版必修3第二章章末训练卷
答 案
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】C
【解析】根据①中由于小区中各个家庭收入水平之间存在明显差别,故①要采用分层抽样的方法;
②中从10名同学中抽取3个参加座谈会,总体容量和样本容量均不大,要采用简单随机抽样的方法,
故选C.
2.【答案】B
【解析】从表中第5行第6列开始向右读取数据,依次得到(舍),(舍),(舍),(舍),(舍),,
由此可得出第8个样本编号是,故选B.
3.【答案】A
【解析】对选项A,因为,所以y与x具有正的线性相关关系,故A正确;
对选项B,回归直线过样本中心,故B正确;
对选项C,因为回归方程为,
所以身高增加,则其体重约增加,故C正确;
对选项D,时,,
但这是预测值,不可断定其体重为,故D错误,
故选A.
4.【答案】C
【解析】由表格中的数据可知,,
由频率分布直方图可知,,,
则,故选C.
5.【答案】B
【解析】设原数据的平均数为,则新数据的平均数为,
则原数据的方差为,
则新数据的方差为:
,
故数据,,…,的标准差为8,故选B.
6.【答案】B
【解析】题图中的相关的点均集中在某条直线的附近,所以线性相关性较强,且该直线的斜率小于1,结合各选项知,选B.
7.【答案】C
【解析】A.根据折线图从2020年2月14日起,中国新增确诊人数几乎为0,
所以A正确;
B.根据折线图可以看出从2020年3月13日至2020年4月3日海外新增确诊人数在小范围内有增有减,但总体上新增确诊人数在快速的增加,所以B正确;
C.由折线图可得这66天海外每天新增新冠肺炎确诊病例数的中位数大约出现在3月18日左右,其值小于,故C不正确;
D.由折线图可得在4月3日到4日和4月15日到16日海外新增新冠肺炎确诊病例数都超过10万例,所以D正确,
故选C.
8.【答案】A
【解析】甲班成绩的中位数是81,故,乙班成绩的平均数是86,
则,解得,
又成等比数列,故,所以,,
当且仅当,时,等号成立,
故选A.
9.【答案】A
【解析】因为甲实得分却记为分,少记20分;
乙实得分却记为分,多记20分,
所以总分没有变化,因此更正前后平均分没有变化,都是80分,
设甲乙之外其他同学的成绩分别为,,,,
因为更正前方差为,
所以,
可得,
更正后平方差
,
故选A.
10.【答案】B
【解析】,
;
,
;
,
,
由,得,故选B.
11.【答案】B
【解析】甲地的个数据的中位数为24,众数为22,则甲地连续天的日平均温度的记录数据中必有,,,其余2天的记录数据大于24,且不相等,
故甲地符合进入夏季的标准;
乙地的个数据的中位数为,总体均值为,当个数据为,,,,时,其连续天的日平均温度中有低于的,此时乙地不符合进入夏季的标准;
丙地的个数据中有个数据是,总体均值为,
设其余个数据分别为,,,,
则总体方差
,
若,,,有小于的数据时,则,即,
不满足题意,
所以,,,均大于或等于,故丙地符合进入夏季的标准,
综上所述,肯定进入夏季的地区有①③,故选B.
12.【答案】C
【解析】∵单价等于时,供给量,
∴当单价小于时,由于,∴供给量,
而此时,需要量,
故此时,供给量需要量;
而当单价等于时,需求量,
∴当单价大于时,∵,∴供给量,
而此时,需要量,
故此时,供给量需要量,
综上所述,市场供需平衡点(即供给量和需求量相等时的单价)应在区间内,
故选C.
二、填空题:本大题共4小题,每小题5分.
13.【答案】331
【解析】由抽取时的分段间隔是20.即抽取20名同学,其编号构成首项为11,公差为20的等差数列,第17组抽取的号码,
故答案为331.
14.【答案】185
【解析】设父亲身高为x cm,儿子身高为y cm,则
x 173 170 176
y 170 176 182
,,
,,
∴,
当时,.
15.【答案】
【解析】依题意,得,
设,,,,的平均数为,
根据方差的计算公式有,
,
即,,
故答案为.
16.【答案】④⑤
【解析】①错,举反例:;其平均数,但不符合上述指标;
②错,举反例:;其标准差,但不符合上述指标;
③错,举反例:;其平均数且标准差,但不符合上述指标;
④对,若极差小于,符合上述指标;
若极差小于或等于,有可能⑴;⑵;⑶;⑷;⑸,
在平均数的条件下,只有⑴⑵⑶成立,符合上述指标;
⑤对,在众数等于且极差小于或等于,则最大数不超过,符合指标,
所以选④⑤.
三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.【答案】(1)6,;(2);(3)32件.
【解析】(1),.
(2)∵,,
∴纯利与每天销售件数之间的回归直线方程为.
(3)当时,,所以,
因此若该店每周至少要获纯利200元,则该店每天至少要销售这种服装32件.
18.【答案】(1),,;(2)中位数是,平均数是.
【解析】(1)由频率统计表可知:,,
由频率分布直方图可知:,
解得.
(2)∵前两组的频率和为;
前三组的频率和为,
∴中位数在内,设中位数为,
则,解得,即中位数为.
平均数为,
∴估计该校学生阅读素养的成绩中位数是,平均数是.
19.【答案】(1),,;(2)元,理由见解析.
【解析】(1)根据表中数据可得,三层共有人,抽样比为,
故应该从甲层抽取人;从乙层抽取人;从丙层抽取人.
(2)将个数据按照从小到大的顺序进行排序,可得:
,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,
为使得的销售员完成目标,只需求出第百分位数即可.
由可知样本数据的第百分位数为第项与第项数据的平均数,
即,
则应该将销售目标定位元比较合理.
20.【答案】(1)件;(2)需要对该工厂设备实施升级改造.
【解析】(1)因为,
解得,
所以200件样本中尺寸在内的样本数为(件).
(2)由题意可得,这批产品中优等品有件,
这批产品中不合格品有件,
这批产品中合格品有件,
元.
所以该工厂生产的产品一个月所获得的利润为8960元,
因为,所以需要对该工厂设备实施升级改造.
21.【答案】(1),众数190,中位数为190;(2)①;②不合格树苗、合格树苗分别应抽取7株和13株.
【解析】(1),
,
众数为,
设中位数为,因为,
,
则,
,.
(2)①树苗高度185cm及以上的频率是,
.
②不合格的抽取株,合格的抽取株,
故不合格树苗、合格树苗分别应抽取7株和13株.
22.【答案】(1);(2);(3).
【解析】(1)由题中散点图可以判断,适宜作为关于的回归方程.
(2)令,则,
原数据变为
由表可知与近似具有线性相关关系,计算得,
,
,
所以,,则,
所以关于的回归方程是.
(3)由(2)得,,
任取、,且,即,
可得,
因为,则,,所以,,
所以,函数在区间上单调递增,则.
统计
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.问题:①某社区有500个家庭,其中高收入家庭125户,中等收入家庭280户,低收入家庭95户,为了了解社会购买力的某项指标,要从中抽出一个容量为100户的样本;②从10名学生中抽出3人参加座谈会,方法:Ⅰ简单随机抽样法;Ⅱ分层抽样法.则问题与方法配对正确的是( )
A.①Ⅰ②Ⅱ B.①Ⅰ②Ⅰ C.①Ⅱ②Ⅰ D.①Ⅱ②Ⅱ
2.某工厂利用随机数表对生产的700个零件进行抽样测试,先将700个零件进行编号,001,002,…,699,700,从中抽取70个样本,下图提供随机数表的第4行到第6行,若从表中第5行第6列开始向右读取数据,则得到的第8个样本编号是( )
A.623 B.368 C.253 D.072
3.设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,,n),用最小二乘法建立的回归方程为.
①y与x具有正的线性相关关系;
②回归直线过样本点的中心;
③若该大学某女生身高增加1cm,则其体重约增加;
④若该大学某女生身高为170cm,则其体重必为.
则上述判断不正确的个数是( )
A.1 B.2 C.3 D.4
4.“脱口秀大赛”上选手的分数分为观众评分和嘉宾评分.组织方将观众评分按照,,分组,绘制频率分布直方图如图所示.嘉宾评分的平均数为,观众评分的平均数为,中位数为,则下列选项正确的是( )
嘉宾
评分 96 97 96 89 97 98
A. B.
C. D.
5.若样本数据,,…,的标准差为,则数据,,…,的标准差为( )
A. B. C. D.
6.为研究语文成绩和英语成绩之间是否具有线性相关关系,统计两科成绩得到如图所示的散点图(两坐标轴单位长度相同),用回归直线近似地刻画其相关关系,根据图形,以下结论最有可能成立的是( )
A.线性相关关系较强,的值为
B.线性相关关系较强,的值为
C.线性相关关系较强,的值为
D.线性相关关系太弱,无研究价值
7.下图是从2020年2月14日至2020年4月19日共66天的新冠肺炎中国/海外新增确诊趋势图,根据该图,下列结论中错误的是( )
A.从2020年2月14日起中国已经基本控制住国内的新冠肺炎疫情
B.从2020年3月13日至2020年4月3日海外新冠肺炎疫情快速恶化
C.这66天海外每天新增新冠肺炎确诊病例数的中位数在区间内
D.海外新增新冠肺炎确诊病例数最多的一天突破10万例
8.甲、乙两班在我校举行的“不忘初心,牢记使命”合唱比赛中,7位评委的评分情况如茎叶图所示,其中甲班成绩的中位数是81,乙班成绩的平均数是86,若正实数满足:成等比数列,则的最小值为( )
A.4 B. C. D.
9.某班名学生,在一次考试中统计平均分为分,方差为,后来发现有两名同学的成绩有误,甲实得分却记为分,乙实得分却记为分,则更正后的方差为( )
A. B. C. D.
10.甲、乙、丙三名射箭运动员在某次测试中各射箭20次,三人的测试成绩如下表:分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有( )
甲的成绩
环数 7 8 9 10
频数 5 5 5 5
乙的成绩
环数 7 8 9 10
频数 6 4 4 6
丙的成绩
环数 7 8 9 10
频数 4 6 6 4
A. B.
C. D.
11.气象意义上从春季进入夏季的标志为“连续天的日平均温度均不低于”.现有甲、乙、丙三地连续天的日平均温度的记录数据(记录数据都是正整数,单位:):
①甲地:个数据的中位数为,众数为;
②乙地:个数据的中位数为,总体均值为;
③丙地:个数据中有个数据是,总体均值为,总体方差为.
其中肯定进入夏季的地区有( )
A.①② B.①③ C.②③ D.①②③
12.某农贸市场出售西红柿,当价格上涨时,供给量相应增加,而需求量相应减少,具体调查结果如下表:
表1 市场供给量
单价(元/ ) 2
4
供给量() 50 60 70 75 80 90
表2 市场需求量
单价(元/) 4
2
需求量() 50 60 65 70 75 80
根据以上提供的信息,市场供需平衡点(即供给量和需求量相等时的单价)应在区间( )
A.内 B.内
C.内 D.内
二、填空题:本大题共4小题,每小题5分.
13.用系统抽样方法从400名学生中抽取容量为20的样本,将400名学生随机地编号为1~400,按编号顺序平均分为20个组.若第1组中用抽签的方法确定抽出的号码为11,则第17组抽取的号码为________.
14.某数学老师身高,他爷爷、父亲和儿子的身高分别是,和.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为________.
15.2020年年初,新冠肺炎疫情袭击全国.口罩成为重要的抗疫物资,为了确保口罩供应,某工厂口罩生产线高速运转,工人加班加点生产.设该工厂连续5天生产的口罩数依次为,,,,(单位:十万只),若这组数据,,,,的方差为,且,,,,的平均数为4,则该工厂这5天平均每天生产口罩__________十万只.
16.在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各个选项中,一定符合上述指标的是__________.
①平均数;②标准差;③平均数且标准差;
④平均数且极差小于或等于2;⑤众数等于1且极差小于或等于4.
三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)某个体服装店经营的某种服装在某周内所获纯利(元)与该周每天销售这种服装的件数(件)之间有一组数据如下表所示.
服装件数(件) 3 4 5 6 7 8 9
某周内所获纯利(元) 66 69 73 81 89 90 91
(1)求,;
(2)若所获纯利(元)与每天销售这种服装的件数(件)之间是线性相关的,求回归直线方程;
(3)若该店每周至少要获利200元,请你预测该店每天至少要销售这种服装多少件?(以下数据供选择:,,)(已知回归系数为,)
18.(12分)某地教育部门对某学校学生的阅读素养进行检测,在该校随机抽取了名学生进行检测,实行百分制,现将所得的成绩按照,,,,,分成6组,并根据所得数据作出了如下所示的频数与频率的统计表和频率分布直方图.
分组 频数 频率
25
10
合计
1
(1)求出表中,及图中的值;
(2)估计该校学生阅读素养的成绩中位数以及平均数.
19.(12分)一家保险公司决定对推销员实行月标管理,按以往月销售额(单位:千元)把推销员分为甲、乙、丙三个层次,各层次人数如下:
甲 乙 丙
月销售额
人数 120 240 90
(1)为了了解推销员对目标设定的意见,决定从甲、乙、丙三个层次中采取比例分配的分层随机抽样抽取30人进行座谈,请计算甲、乙、丙三个层次各应抽取多少人?
(2)确定销售日标是否合适,直接影响到公司的经济效益,如果目标定得过高,多数推销员完不成任务,会使推销员失去信心;如果目标定得太低,将不利于挖掘推销员的工作潜力.现已知按上面的方法抽取了部分推销员的月销售额(单位:千元):
公司为了使70%的推销员能够完成销售目标,根据这组样本数据,应将销售目标定为多少比较合理?
20.(12分)为了了解某工厂生产的产品情况,从该工厂生产的产品随机抽取了一个容量为200的样本,测量它们的尺寸(单位:),数据分为,,,,,,七组,其频率分布直方图如图所示.
(1)根据频率分布直方图,求200件样本中尺寸在内的样本数;
(2)记产品尺寸在内为等品,每件可获利6元;产品尺寸在内为不合格品,每件亏损3元;其余的为合格品,每件可获利4元.若该机器一个月共生产2000件产品.以样本的频率代替总体在各组的频率,若单月利润未能达到9000元,则需要对该工厂设备实施升级改造.试判断是否需要对该工厂设备实施升级改造.
21.(12分)6月17日是联合国确定的“世界防治荒漠化和干旱日”,为增强全社会对防治荒漠化的认识与关注,聚焦联合国2030可持续发展目标——实现全球土地退化零增长.自2004年以来,我国荒漠化和沙化状况呈现整体遏制、持续缩减、功能增强、成效明显的良好态势.治理沙漠离不开优质的树苗,现从苗圃中随机地抽测了200株树苗的高度(单位:cm),得到以下频率分布直方图.
(1)求直方图中的值及众数、中位数;
(2)若树高185cm及以上是可以移栽的合格树苗.
①求合格树苗的平均高度(结果精确到个位);
②从样本中按分层抽样方法抽取20株树苗作进一步研究,不合格树苗、合格树苗分别应抽取多少株?
22.(12分)在一次抽样调查中测得个样本点,得到下表及散点图.
(1)根据散点图判断与,哪一个适宜作为关于的回归方程;(给出判断即可,不必说明理由)
(2)根据(1)的判断结果试建立与的回归方程;(计算结果保留整数)
(3)在(2)的条件下,设且,试求的最小值.
参考公式:回归方程中,,.
人教A版必修3第二章章末训练卷
答 案
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】C
【解析】根据①中由于小区中各个家庭收入水平之间存在明显差别,故①要采用分层抽样的方法;
②中从10名同学中抽取3个参加座谈会,总体容量和样本容量均不大,要采用简单随机抽样的方法,
故选C.
2.【答案】B
【解析】从表中第5行第6列开始向右读取数据,依次得到(舍),(舍),(舍),(舍),(舍),,
由此可得出第8个样本编号是,故选B.
3.【答案】A
【解析】对选项A,因为,所以y与x具有正的线性相关关系,故A正确;
对选项B,回归直线过样本中心,故B正确;
对选项C,因为回归方程为,
所以身高增加,则其体重约增加,故C正确;
对选项D,时,,
但这是预测值,不可断定其体重为,故D错误,
故选A.
4.【答案】C
【解析】由表格中的数据可知,,
由频率分布直方图可知,,,
则,故选C.
5.【答案】B
【解析】设原数据的平均数为,则新数据的平均数为,
则原数据的方差为,
则新数据的方差为:
,
故数据,,…,的标准差为8,故选B.
6.【答案】B
【解析】题图中的相关的点均集中在某条直线的附近,所以线性相关性较强,且该直线的斜率小于1,结合各选项知,选B.
7.【答案】C
【解析】A.根据折线图从2020年2月14日起,中国新增确诊人数几乎为0,
所以A正确;
B.根据折线图可以看出从2020年3月13日至2020年4月3日海外新增确诊人数在小范围内有增有减,但总体上新增确诊人数在快速的增加,所以B正确;
C.由折线图可得这66天海外每天新增新冠肺炎确诊病例数的中位数大约出现在3月18日左右,其值小于,故C不正确;
D.由折线图可得在4月3日到4日和4月15日到16日海外新增新冠肺炎确诊病例数都超过10万例,所以D正确,
故选C.
8.【答案】A
【解析】甲班成绩的中位数是81,故,乙班成绩的平均数是86,
则,解得,
又成等比数列,故,所以,,
当且仅当,时,等号成立,
故选A.
9.【答案】A
【解析】因为甲实得分却记为分,少记20分;
乙实得分却记为分,多记20分,
所以总分没有变化,因此更正前后平均分没有变化,都是80分,
设甲乙之外其他同学的成绩分别为,,,,
因为更正前方差为,
所以,
可得,
更正后平方差
,
故选A.
10.【答案】B
【解析】,
;
,
;
,
,
由,得,故选B.
11.【答案】B
【解析】甲地的个数据的中位数为24,众数为22,则甲地连续天的日平均温度的记录数据中必有,,,其余2天的记录数据大于24,且不相等,
故甲地符合进入夏季的标准;
乙地的个数据的中位数为,总体均值为,当个数据为,,,,时,其连续天的日平均温度中有低于的,此时乙地不符合进入夏季的标准;
丙地的个数据中有个数据是,总体均值为,
设其余个数据分别为,,,,
则总体方差
,
若,,,有小于的数据时,则,即,
不满足题意,
所以,,,均大于或等于,故丙地符合进入夏季的标准,
综上所述,肯定进入夏季的地区有①③,故选B.
12.【答案】C
【解析】∵单价等于时,供给量,
∴当单价小于时,由于,∴供给量,
而此时,需要量,
故此时,供给量需要量;
而当单价等于时,需求量,
∴当单价大于时,∵,∴供给量,
而此时,需要量,
故此时,供给量需要量,
综上所述,市场供需平衡点(即供给量和需求量相等时的单价)应在区间内,
故选C.
二、填空题:本大题共4小题,每小题5分.
13.【答案】331
【解析】由抽取时的分段间隔是20.即抽取20名同学,其编号构成首项为11,公差为20的等差数列,第17组抽取的号码,
故答案为331.
14.【答案】185
【解析】设父亲身高为x cm,儿子身高为y cm,则
x 173 170 176
y 170 176 182
,,
,,
∴,
当时,.
15.【答案】
【解析】依题意,得,
设,,,,的平均数为,
根据方差的计算公式有,
,
即,,
故答案为.
16.【答案】④⑤
【解析】①错,举反例:;其平均数,但不符合上述指标;
②错,举反例:;其标准差,但不符合上述指标;
③错,举反例:;其平均数且标准差,但不符合上述指标;
④对,若极差小于,符合上述指标;
若极差小于或等于,有可能⑴;⑵;⑶;⑷;⑸,
在平均数的条件下,只有⑴⑵⑶成立,符合上述指标;
⑤对,在众数等于且极差小于或等于,则最大数不超过,符合指标,
所以选④⑤.
三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.【答案】(1)6,;(2);(3)32件.
【解析】(1),.
(2)∵,,
∴纯利与每天销售件数之间的回归直线方程为.
(3)当时,,所以,
因此若该店每周至少要获纯利200元,则该店每天至少要销售这种服装32件.
18.【答案】(1),,;(2)中位数是,平均数是.
【解析】(1)由频率统计表可知:,,
由频率分布直方图可知:,
解得.
(2)∵前两组的频率和为;
前三组的频率和为,
∴中位数在内,设中位数为,
则,解得,即中位数为.
平均数为,
∴估计该校学生阅读素养的成绩中位数是,平均数是.
19.【答案】(1),,;(2)元,理由见解析.
【解析】(1)根据表中数据可得,三层共有人,抽样比为,
故应该从甲层抽取人;从乙层抽取人;从丙层抽取人.
(2)将个数据按照从小到大的顺序进行排序,可得:
,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,
为使得的销售员完成目标,只需求出第百分位数即可.
由可知样本数据的第百分位数为第项与第项数据的平均数,
即,
则应该将销售目标定位元比较合理.
20.【答案】(1)件;(2)需要对该工厂设备实施升级改造.
【解析】(1)因为,
解得,
所以200件样本中尺寸在内的样本数为(件).
(2)由题意可得,这批产品中优等品有件,
这批产品中不合格品有件,
这批产品中合格品有件,
元.
所以该工厂生产的产品一个月所获得的利润为8960元,
因为,所以需要对该工厂设备实施升级改造.
21.【答案】(1),众数190,中位数为190;(2)①;②不合格树苗、合格树苗分别应抽取7株和13株.
【解析】(1),
,
众数为,
设中位数为,因为,
,
则,
,.
(2)①树苗高度185cm及以上的频率是,
.
②不合格的抽取株,合格的抽取株,
故不合格树苗、合格树苗分别应抽取7株和13株.
22.【答案】(1);(2);(3).
【解析】(1)由题中散点图可以判断,适宜作为关于的回归方程.
(2)令,则,
原数据变为
由表可知与近似具有线性相关关系,计算得,
,
,
所以,,则,
所以关于的回归方程是.
(3)由(2)得,,
任取、,且,即,
可得,
因为,则,,所以,,
所以,函数在区间上单调递增,则.
