2020-2021学年九年级下册数学北师大新版《第3章 圆》单元测试题(word版含解析)
文档属性
| 名称 | 2020-2021学年九年级下册数学北师大新版《第3章 圆》单元测试题(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 366.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 00:00:00 | ||
图片预览




文档简介
2020-2021学年九年级下册数学北师大新版《第3章
圆》单元测试题
一.选择题
1.下列说法正确的是( )
A.长度相等的两条弧是等弧
B.优弧一定大于劣弧
C.直径是圆中最长的弦
D.不同的圆中不可能有相等的弦
2.在圆柱形油槽内装有一些油,截面如图,油面宽AB为6dm,如果再注入一些油后,油面AB上升1dm,油面宽为8dm,圆柱形油槽直径MN为( )
A.6dm
B.8dm
C.10dm
D.12dm
3.如图所示,AB是直径,点E是弧AB中点,弦CD∥AB且平分OE,连AD,∠BAD度数为( )
A.45°
B.30°
C.15°
D.10
4.如图,两个半径都是4cm的圆外切于点C,一只蚂蚁由点A开始依A、B、C、D、E、F、C、G、A的顺序沿着圆周上的8段长度相等的路径绕行,蚂蚁在这8段路径上不断爬行,直到行走2006πcm后才停下来,则蚂蚁停的那一个点为( )
A.D点
B.E点
C.F点
D.G点
5.如图,若OB=5,AB=8,则AC的长为( )
A.
B.8
C.10
D.6
6.在平行四边形、矩形、正方形、菱形、等腰梯形、直角梯形中,必定存在外接圆的有( )
A.1个
B.2个
C.3个
D.4个
7.如图,等边三角形ABC中,AD⊥BC于D,△ABD的内切⊙O的半径为R,另有一个⊙O1与AB,BD,⊙O都相切,其半径为r1,则⊙O与⊙O1的面积之比为( )
A.1:9
B.9:1
C.8:1
D.与R,r1的取值有关
8.如图,△ABC中,∠A=60°,BC=6,它的周长为16.若⊙O与BC,AC,AB三边分别切于E,F,D点,则DF的长为( )
A.2
B.3
C.4
D.6
9.圆内接正方形的面积为a,则圆的面积为( )
A.2πa
B.
C.
D.以上都不对
10.已知⊙O半径为5,OP=8,点Q在⊙O上运动,设PQ的最大值为m,最小值为n,则m﹣n的值为( )
A.5
B.10
C.12
D.8
二.填空题
11.圆内接正五边形中,每个外角的度数=
度.
12.如图,已知半圆O的直径为AB,半径长为,点C在AB上,OC=,CD⊥AB,CD交半圆O于D,那么与半圆相切,且与BC,CD相切的圆O'的半径长是
.
13.已知,⊙O的直径为10cm,点O到直线a的距离为d:①若a与⊙O相切,则d=
cm;②若d=4cm,则a与⊙O有
个交点;③若d=6cm,则a与⊙O的位置关系是
.
14.如图,AB是⊙O的直径,若∠C=58°,则∠D=
.
15.如图所示,AB、CD是⊙O的直径,⊙O的半径为R,AB⊥CD,以B为圆心,以BC为半径作弧CED,则弧CED与弧CAD围成的新月形ACED的面积为
.
16.如图:⊙O内切于弓形ADB的最大的圆,且弧ADB的度数为120°,则⊙O的周长与弧AB的长的比是
.
17.如图,△ABC的内切圆⊙O分别切AB,AC,BC于F,E,D,若∠A=70°,则∠BOC=
度,∠EDF=
度.
18.在△ABC中,∠A=62°,点I是外接圆圆心,则∠BIC=
度.
19.点P是半径为5的⊙O内一点,且OP=4,在过P点的所有⊙O的弦中,最短弦的长为
.
20.在⊙O中,有两条弦AB和CD,如果=2,那么弦AB和2CD的大小关系为AB
2CD.
三.解答题
21.已知:如图,AB是⊙O的直径,OD⊥BC于D,AC=8cm,求OD的长.
22.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.
(1)求证:BD平分∠ABC;
(2)当BC=CE=2时,求DE的长度.
23.如图,以Rt△ABC的直角边AC为直径作⊙O,交斜边AB于点D,E为BC边的中点,连DE.
(1)请判断DE是否为⊙O的切线,并证明你的结论.
(2)当AD:DB=9:16时,DE=8cm时,求⊙O的半径R.
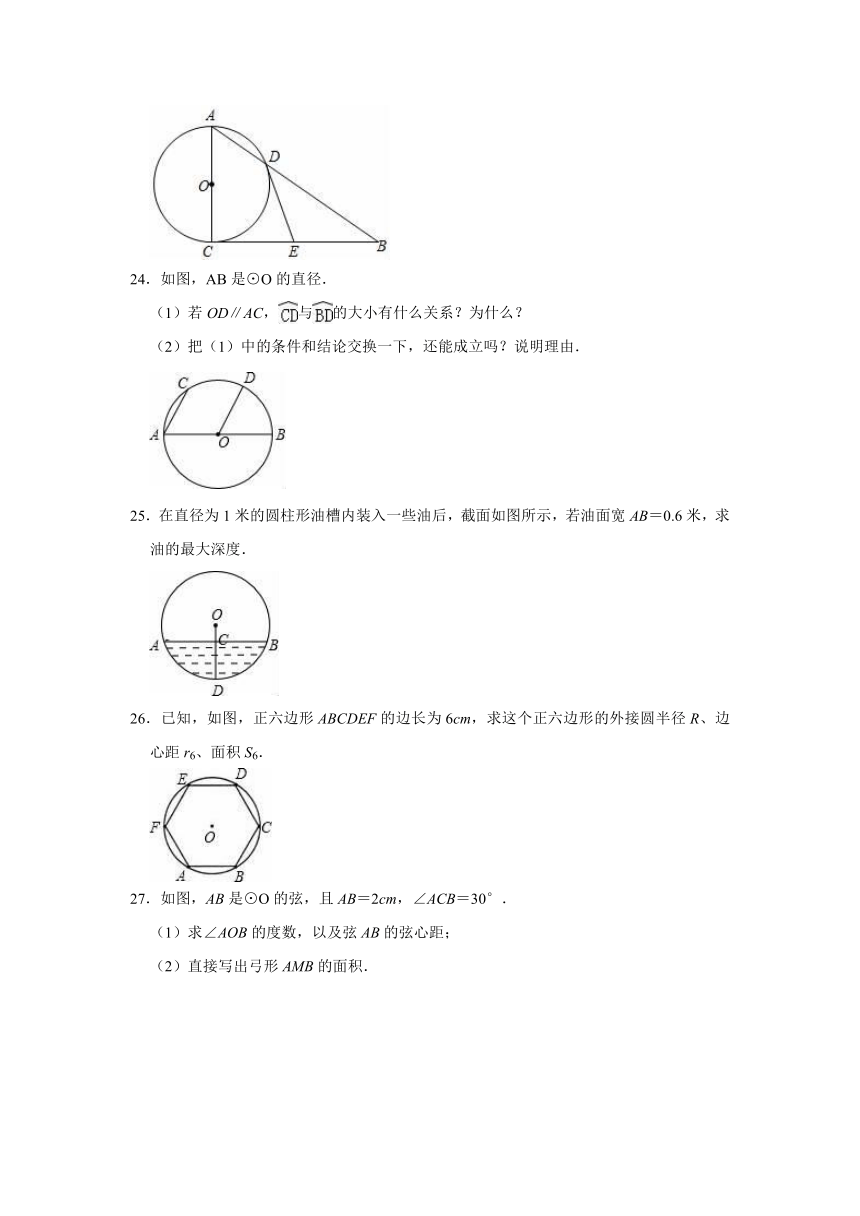
24.如图,AB是⊙O的直径.
(1)若OD∥AC,与的大小有什么关系?为什么?
(2)把(1)中的条件和结论交换一下,还能成立吗?说明理由.
25.在直径为1米的圆柱形油槽内装入一些油后,截面如图所示,若油面宽AB=0.6米,求油的最大深度.
26.已知,如图,正六边形ABCDEF的边长为6cm,求这个正六边形的外接圆半径R、边心距r6、面积S6.
27.如图,AB是⊙O的弦,且AB=2cm,∠ACB=30°.
(1)求∠AOB的度数,以及弦AB的弦心距;
(2)直接写出弓形AMB的面积.
28.某公司计划砌一个形状如图1所示的喷水池,经人建议人为如图2所示的形状,且外圆的半径不变,只是担心原来准备好的材料不够,请你比较两种方案,哪一种需要的材料多?
参考答案与试题解析
一.选择题
1.解:A、长度相等的两条弧不一定能重合,由等弧的概念可知,A错误.
B、必须在同圆或等圆中,优弧才大于劣弧,故B错误.
C、直径是过圆心的弦,也是圆内最长的弦,故C正确.
D、弦是连接圆上两点的线段,不同的圆中,可能有相等的弦,故D错误.
故选:C.
2.解:根据题意画出图形,如图所示,EF=1dm,AB=6dm,CD=8dm,设圆的半径为r,
∵OE⊥CD,OF⊥AB,
∴CE=DE=4dm,AF=BF=3dm,
在Rt△OCE和△OAF中,
根据勾股定理得:OE==,OF==,
∴OE﹣OF=1,即﹣=1,
=+1,
两边平方得,r2﹣9=r2﹣16+2+1,
=3,
两边平方得,r2﹣16=9,
r2=25,
解得:r=5,
则圆柱形油槽直径MN为10dm.
故选:C.
3.解:设CD与OE交于P,则连接OC,∵CD∥AB且平分OE,∴OP=?OC,
∴sin∠PCO=,
∴∠PCO=30°,
又∵CD∥AB,∴∠COA=∠PCO=30°,
∴∠BAD=∠BOD=15°.
故选:C.
4.解:C=π×8=8π,
2C=16π,
2006π=16π×125+6π,
所以停止在D点.
故选:A.
5.解:CD垂直AB于E,如图,则AE=BE=AB=×8=4,
在Rt△OBE中,OE===3,
∴CE=OE+OC=3+5=8,
在Rt△ACE中,AC===4.
故选:A.
6.解:根据圆内接多边形的性质可得:矩形,正方形与等腰梯形必定存在外接圆.故选C.
7.解:∵R+r1=2(R﹣r1),即R=3r1,
∴⊙O与⊙O1的面积之比为9:1.
故选:B.
8.解:∵⊙O与BC,AC,AB三边分别切于E,F,D点,
∴AD=AF,BE=BD,CE=CF,
∵BC=BE+CE=6,
∴BD+CF=6,
∵AD=AF,∠A=60°,
∴△ADF是等边三角形,
∴AD=AF=DF,
∵AB+AC+BC=16,BC=6,
∴AB+AC=10,
∵BD+CF=6,
∴AD+AF=4,
∵AD=AF=DF,
∴DF=AF=AD=×4=2,
故选:A.
9.解:∵圆内接正方形的面积为a,
则正方形的边长为,正方形的外接圆的半径为,
∴圆的面积为.
故选:B.
10.解:如图,m=PQ1=OP+OQ,n=PQ2=OP﹣OQ,
∴m﹣n=OP+OQ﹣(OP﹣OQ)=2OQ=10,
故选:B.
二.填空题
11.解:360°÷5=72°.
故答案为:72.
12.解:设⊙O'与半圆、BC、CD相切的切点分别为E、F、M,连接O'M,O'F,连接OO'并延长经过切点E,
则OO'=OE﹣O'E,O'M=O'F,
∵⊙O'与BC,CD相切,
∴O'F⊥OB,O'M⊥CD,
∴∠O'FA=90°,∠O'MC=90°,
∵CD⊥AB,
∴∠MCF=90°,
∴四边形O'MCF为正方形,
∴O'M=FC,
设O'F=x,则OF=x+,
∵O'F2+OF2=OO'2,
∴,
解得x1=2,x2=﹣18(舍去),
∴圆O'的半径长为2.
故答案为:2.
13.解:∵⊙O的直径为10cm,
∴⊙O的半径r=5cm.
①∵直线和圆相切,
∴d=r,则d=5cm;
②∵d=4cm<r=5cm,
∴直线和圆相交,
∴直线与圆有两个公共点;
③∵d=6cm>r=5cm,
∴直线a和⊙O相离.
14.解:连接OE,
∵∠C=58°,
∴∠AOE=2∠C=116°,
∵AB是⊙O的直径,
∴∠BOE=180°﹣∠AOE=64°,
∴∠D=∠BOE=32°.
故答案为:32°.
15.解:∵DC为直径,
∴∠CBD=90°,
∵AB⊥CD,
∴∠COB=90°,
∴BC=BD===R,
∴弧CED与弧CAD围成的新月形ACED的面积S=S△CBD+S圆O﹣S扇形CBD=R×R+R2﹣=R2,
故答案为:R2.
16.解:如图,确定弓形的圆心P,连接PB、PD,根据题意可知CD是⊙O的直径,PB,PD是⊙P的半径.
∵⊙O内切于弓形ADB的最大的圆,且弧ADB的度数为120°
∴PD⊥AB,∠BPD=60°
设PB=1,则PC=CD=
⊙O的周长是π,
弧AB的长是π,
∴⊙O的周长与弧AB的长的比是π:π=3:4,即.
17.解:∵O是△ABC的内心,
∴OB、OC是∠ABC、∠ACB的角平分线;
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°﹣70°)=55°;
∴∠BOC=180°﹣55°=125°.
∵CA、CB分别切⊙O于E、D,
∴CE=CD;又OC平分∠BCA,
∴OC⊥DE;
同理可得:OB⊥DF;
∴∠FDE=180°﹣∠BOC=55°.
18.解:∠BIC=2∠A=124°.
19.解:如图,∵OP⊥AB,OP=4,OB=5,
∴PB==3,
∴AB=2PB=6.
故答案为:6.
20.解:如图,取的中点E,连接AE,BE,
∵在⊙O中,=2,
∴==,
∴AE=BE=CD,
∵AE+BE>AB,
∴AB<2CD.
故答案为:<.
三.解答题
21.解:∵AB是⊙O的直径,
∴∠C=90°,
∵OD⊥BC,
∴∠BDO=∠C=90°,
∴OD∥AC,
∵OA=OB,
∴CD=BD,
即OD是△ABC的中位线,
∴OD=AC=×8=4(cm).
22.(1)证明:∵OD⊥AC,
∴=,
∴∠ABD=∠CBD,
∴BD平分∠ABC;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵OD⊥AC,
∴AE=CE=2,
在Rt△ABC中,AB==2,
∴OD=,
∵AE=CE,OA=OB,
∴OE为△ABC的中位线,
∴OE=BC=1,
∴DE=﹣1.
23.解:(1)DE是⊙O的切线,
证明:连接OE,OD;
在Rt△CDB,E为BC边的中点,
∴CE=DE.
在△OEC和△ODC中,
,
∴△OEC≌Rt△ODC(SSS).
∴∠ODC=∠OCE=90°.
∴DE是⊙O的切线.
(2)连接CD,
∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠BDC=90°,
∵E为BC的中点,
∴BC=2DE=16(cm),
∵∠BDC=∠ACB,∠B=∠B,
∴△BCD∽△BAC,
∴,
∴BC2=BD?AB,
设AD=9xcm(x>0),BD=16xcm,
∴162=25x?16x,
∴x=(负值舍去).
∴AB=20,AC=12.
∴⊙O的半径R=6(cm).
24.解:(1).
证明:延长DO交⊙O于E,
∵AC∥OD
∴
∵∠1=∠2
∴
∴;
(2)仍成立.
证明:延长DO交⊙O于点E,连接AD,
∵,
∴
∴∠3=∠D
∴AC∥OD.
25.解:连接OA.
∵OA=OD=0.5米,AC=AB=0.3米
∴OC2=OA2﹣AC2
∴OC==0.4米
∴CD=OD﹣OC=0.5﹣0.4=0.1米
故油的最大深度是0.1米.
26.解:连接OA,OB,过点O作OG⊥AB于G,
∵∠AOB=60°,OA=OB,
∴△AOB是等边三角形,
∴OA=OB=6,即R=6,
∵OA=OB=6,OG⊥AB,
∴AG=AB=×6=3,
∴在Rt△AOG中,r6=OG==3cm,
∴S6=×6×6×3=54cm2.
27.解:(1)过O作OD⊥AB于D,
∵∠ACB=30°.
∴∠AOB=2∠ACB=60°(一条弧所对的圆周角等于圆心角的一半),
∵OD过O,OD⊥AB,
∴AD=BD=AB=2=1(cm),
∵OA=OB,∠AOB=60°,
∴△AOB是等边三角形,
∴OA=OB=AB=2cm,
由勾股定理得:OD===(cm),
即弦AB的弦心距是cm;
(2)弓形AMB的面积是(π﹣)cm2,
理由是:S弓形=扇形AOB﹣S△AOB=60﹣=(π﹣)cm2.
28.解:一样多,设图示中的大圆的半径为R,每个小圆的半径为r1,r2,r3,r4
且r1+r2+r3+r4=R,则四个小圆的周长为2π(r1+r2+r3+r4)=2πR=大圆的周长,
故用的材料一样多.
圆》单元测试题
一.选择题
1.下列说法正确的是( )
A.长度相等的两条弧是等弧
B.优弧一定大于劣弧
C.直径是圆中最长的弦
D.不同的圆中不可能有相等的弦
2.在圆柱形油槽内装有一些油,截面如图,油面宽AB为6dm,如果再注入一些油后,油面AB上升1dm,油面宽为8dm,圆柱形油槽直径MN为( )
A.6dm
B.8dm
C.10dm
D.12dm
3.如图所示,AB是直径,点E是弧AB中点,弦CD∥AB且平分OE,连AD,∠BAD度数为( )
A.45°
B.30°
C.15°
D.10
4.如图,两个半径都是4cm的圆外切于点C,一只蚂蚁由点A开始依A、B、C、D、E、F、C、G、A的顺序沿着圆周上的8段长度相等的路径绕行,蚂蚁在这8段路径上不断爬行,直到行走2006πcm后才停下来,则蚂蚁停的那一个点为( )
A.D点
B.E点
C.F点
D.G点
5.如图,若OB=5,AB=8,则AC的长为( )
A.
B.8
C.10
D.6
6.在平行四边形、矩形、正方形、菱形、等腰梯形、直角梯形中,必定存在外接圆的有( )
A.1个
B.2个
C.3个
D.4个
7.如图,等边三角形ABC中,AD⊥BC于D,△ABD的内切⊙O的半径为R,另有一个⊙O1与AB,BD,⊙O都相切,其半径为r1,则⊙O与⊙O1的面积之比为( )
A.1:9
B.9:1
C.8:1
D.与R,r1的取值有关
8.如图,△ABC中,∠A=60°,BC=6,它的周长为16.若⊙O与BC,AC,AB三边分别切于E,F,D点,则DF的长为( )
A.2
B.3
C.4
D.6
9.圆内接正方形的面积为a,则圆的面积为( )
A.2πa
B.
C.
D.以上都不对
10.已知⊙O半径为5,OP=8,点Q在⊙O上运动,设PQ的最大值为m,最小值为n,则m﹣n的值为( )
A.5
B.10
C.12
D.8
二.填空题
11.圆内接正五边形中,每个外角的度数=
度.
12.如图,已知半圆O的直径为AB,半径长为,点C在AB上,OC=,CD⊥AB,CD交半圆O于D,那么与半圆相切,且与BC,CD相切的圆O'的半径长是
.
13.已知,⊙O的直径为10cm,点O到直线a的距离为d:①若a与⊙O相切,则d=
cm;②若d=4cm,则a与⊙O有
个交点;③若d=6cm,则a与⊙O的位置关系是
.
14.如图,AB是⊙O的直径,若∠C=58°,则∠D=
.
15.如图所示,AB、CD是⊙O的直径,⊙O的半径为R,AB⊥CD,以B为圆心,以BC为半径作弧CED,则弧CED与弧CAD围成的新月形ACED的面积为
.
16.如图:⊙O内切于弓形ADB的最大的圆,且弧ADB的度数为120°,则⊙O的周长与弧AB的长的比是
.
17.如图,△ABC的内切圆⊙O分别切AB,AC,BC于F,E,D,若∠A=70°,则∠BOC=
度,∠EDF=
度.
18.在△ABC中,∠A=62°,点I是外接圆圆心,则∠BIC=
度.
19.点P是半径为5的⊙O内一点,且OP=4,在过P点的所有⊙O的弦中,最短弦的长为
.
20.在⊙O中,有两条弦AB和CD,如果=2,那么弦AB和2CD的大小关系为AB
2CD.
三.解答题
21.已知:如图,AB是⊙O的直径,OD⊥BC于D,AC=8cm,求OD的长.
22.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.
(1)求证:BD平分∠ABC;
(2)当BC=CE=2时,求DE的长度.
23.如图,以Rt△ABC的直角边AC为直径作⊙O,交斜边AB于点D,E为BC边的中点,连DE.
(1)请判断DE是否为⊙O的切线,并证明你的结论.
(2)当AD:DB=9:16时,DE=8cm时,求⊙O的半径R.
24.如图,AB是⊙O的直径.
(1)若OD∥AC,与的大小有什么关系?为什么?
(2)把(1)中的条件和结论交换一下,还能成立吗?说明理由.
25.在直径为1米的圆柱形油槽内装入一些油后,截面如图所示,若油面宽AB=0.6米,求油的最大深度.
26.已知,如图,正六边形ABCDEF的边长为6cm,求这个正六边形的外接圆半径R、边心距r6、面积S6.
27.如图,AB是⊙O的弦,且AB=2cm,∠ACB=30°.
(1)求∠AOB的度数,以及弦AB的弦心距;
(2)直接写出弓形AMB的面积.
28.某公司计划砌一个形状如图1所示的喷水池,经人建议人为如图2所示的形状,且外圆的半径不变,只是担心原来准备好的材料不够,请你比较两种方案,哪一种需要的材料多?
参考答案与试题解析
一.选择题
1.解:A、长度相等的两条弧不一定能重合,由等弧的概念可知,A错误.
B、必须在同圆或等圆中,优弧才大于劣弧,故B错误.
C、直径是过圆心的弦,也是圆内最长的弦,故C正确.
D、弦是连接圆上两点的线段,不同的圆中,可能有相等的弦,故D错误.
故选:C.
2.解:根据题意画出图形,如图所示,EF=1dm,AB=6dm,CD=8dm,设圆的半径为r,
∵OE⊥CD,OF⊥AB,
∴CE=DE=4dm,AF=BF=3dm,
在Rt△OCE和△OAF中,
根据勾股定理得:OE==,OF==,
∴OE﹣OF=1,即﹣=1,
=+1,
两边平方得,r2﹣9=r2﹣16+2+1,
=3,
两边平方得,r2﹣16=9,
r2=25,
解得:r=5,
则圆柱形油槽直径MN为10dm.
故选:C.
3.解:设CD与OE交于P,则连接OC,∵CD∥AB且平分OE,∴OP=?OC,
∴sin∠PCO=,
∴∠PCO=30°,
又∵CD∥AB,∴∠COA=∠PCO=30°,
∴∠BAD=∠BOD=15°.
故选:C.
4.解:C=π×8=8π,
2C=16π,
2006π=16π×125+6π,
所以停止在D点.
故选:A.
5.解:CD垂直AB于E,如图,则AE=BE=AB=×8=4,
在Rt△OBE中,OE===3,
∴CE=OE+OC=3+5=8,
在Rt△ACE中,AC===4.
故选:A.
6.解:根据圆内接多边形的性质可得:矩形,正方形与等腰梯形必定存在外接圆.故选C.
7.解:∵R+r1=2(R﹣r1),即R=3r1,
∴⊙O与⊙O1的面积之比为9:1.
故选:B.
8.解:∵⊙O与BC,AC,AB三边分别切于E,F,D点,
∴AD=AF,BE=BD,CE=CF,
∵BC=BE+CE=6,
∴BD+CF=6,
∵AD=AF,∠A=60°,
∴△ADF是等边三角形,
∴AD=AF=DF,
∵AB+AC+BC=16,BC=6,
∴AB+AC=10,
∵BD+CF=6,
∴AD+AF=4,
∵AD=AF=DF,
∴DF=AF=AD=×4=2,
故选:A.
9.解:∵圆内接正方形的面积为a,
则正方形的边长为,正方形的外接圆的半径为,
∴圆的面积为.
故选:B.
10.解:如图,m=PQ1=OP+OQ,n=PQ2=OP﹣OQ,
∴m﹣n=OP+OQ﹣(OP﹣OQ)=2OQ=10,
故选:B.
二.填空题
11.解:360°÷5=72°.
故答案为:72.
12.解:设⊙O'与半圆、BC、CD相切的切点分别为E、F、M,连接O'M,O'F,连接OO'并延长经过切点E,
则OO'=OE﹣O'E,O'M=O'F,
∵⊙O'与BC,CD相切,
∴O'F⊥OB,O'M⊥CD,
∴∠O'FA=90°,∠O'MC=90°,
∵CD⊥AB,
∴∠MCF=90°,
∴四边形O'MCF为正方形,
∴O'M=FC,
设O'F=x,则OF=x+,
∵O'F2+OF2=OO'2,
∴,
解得x1=2,x2=﹣18(舍去),
∴圆O'的半径长为2.
故答案为:2.
13.解:∵⊙O的直径为10cm,
∴⊙O的半径r=5cm.
①∵直线和圆相切,
∴d=r,则d=5cm;
②∵d=4cm<r=5cm,
∴直线和圆相交,
∴直线与圆有两个公共点;
③∵d=6cm>r=5cm,
∴直线a和⊙O相离.
14.解:连接OE,
∵∠C=58°,
∴∠AOE=2∠C=116°,
∵AB是⊙O的直径,
∴∠BOE=180°﹣∠AOE=64°,
∴∠D=∠BOE=32°.
故答案为:32°.
15.解:∵DC为直径,
∴∠CBD=90°,
∵AB⊥CD,
∴∠COB=90°,
∴BC=BD===R,
∴弧CED与弧CAD围成的新月形ACED的面积S=S△CBD+S圆O﹣S扇形CBD=R×R+R2﹣=R2,
故答案为:R2.
16.解:如图,确定弓形的圆心P,连接PB、PD,根据题意可知CD是⊙O的直径,PB,PD是⊙P的半径.
∵⊙O内切于弓形ADB的最大的圆,且弧ADB的度数为120°
∴PD⊥AB,∠BPD=60°
设PB=1,则PC=CD=
⊙O的周长是π,
弧AB的长是π,
∴⊙O的周长与弧AB的长的比是π:π=3:4,即.
17.解:∵O是△ABC的内心,
∴OB、OC是∠ABC、∠ACB的角平分线;
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°﹣70°)=55°;
∴∠BOC=180°﹣55°=125°.
∵CA、CB分别切⊙O于E、D,
∴CE=CD;又OC平分∠BCA,
∴OC⊥DE;
同理可得:OB⊥DF;
∴∠FDE=180°﹣∠BOC=55°.
18.解:∠BIC=2∠A=124°.
19.解:如图,∵OP⊥AB,OP=4,OB=5,
∴PB==3,
∴AB=2PB=6.
故答案为:6.
20.解:如图,取的中点E,连接AE,BE,
∵在⊙O中,=2,
∴==,
∴AE=BE=CD,
∵AE+BE>AB,
∴AB<2CD.
故答案为:<.
三.解答题
21.解:∵AB是⊙O的直径,
∴∠C=90°,
∵OD⊥BC,
∴∠BDO=∠C=90°,
∴OD∥AC,
∵OA=OB,
∴CD=BD,
即OD是△ABC的中位线,
∴OD=AC=×8=4(cm).
22.(1)证明:∵OD⊥AC,
∴=,
∴∠ABD=∠CBD,
∴BD平分∠ABC;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵OD⊥AC,
∴AE=CE=2,
在Rt△ABC中,AB==2,
∴OD=,
∵AE=CE,OA=OB,
∴OE为△ABC的中位线,
∴OE=BC=1,
∴DE=﹣1.
23.解:(1)DE是⊙O的切线,
证明:连接OE,OD;
在Rt△CDB,E为BC边的中点,
∴CE=DE.
在△OEC和△ODC中,
,
∴△OEC≌Rt△ODC(SSS).
∴∠ODC=∠OCE=90°.
∴DE是⊙O的切线.
(2)连接CD,
∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠BDC=90°,
∵E为BC的中点,
∴BC=2DE=16(cm),
∵∠BDC=∠ACB,∠B=∠B,
∴△BCD∽△BAC,
∴,
∴BC2=BD?AB,
设AD=9xcm(x>0),BD=16xcm,
∴162=25x?16x,
∴x=(负值舍去).
∴AB=20,AC=12.
∴⊙O的半径R=6(cm).
24.解:(1).
证明:延长DO交⊙O于E,
∵AC∥OD
∴
∵∠1=∠2
∴
∴;
(2)仍成立.
证明:延长DO交⊙O于点E,连接AD,
∵,
∴
∴∠3=∠D
∴AC∥OD.
25.解:连接OA.
∵OA=OD=0.5米,AC=AB=0.3米
∴OC2=OA2﹣AC2
∴OC==0.4米
∴CD=OD﹣OC=0.5﹣0.4=0.1米
故油的最大深度是0.1米.
26.解:连接OA,OB,过点O作OG⊥AB于G,
∵∠AOB=60°,OA=OB,
∴△AOB是等边三角形,
∴OA=OB=6,即R=6,
∵OA=OB=6,OG⊥AB,
∴AG=AB=×6=3,
∴在Rt△AOG中,r6=OG==3cm,
∴S6=×6×6×3=54cm2.
27.解:(1)过O作OD⊥AB于D,
∵∠ACB=30°.
∴∠AOB=2∠ACB=60°(一条弧所对的圆周角等于圆心角的一半),
∵OD过O,OD⊥AB,
∴AD=BD=AB=2=1(cm),
∵OA=OB,∠AOB=60°,
∴△AOB是等边三角形,
∴OA=OB=AB=2cm,
由勾股定理得:OD===(cm),
即弦AB的弦心距是cm;
(2)弓形AMB的面积是(π﹣)cm2,
理由是:S弓形=扇形AOB﹣S△AOB=60﹣=(π﹣)cm2.
28.解:一样多,设图示中的大圆的半径为R,每个小圆的半径为r1,r2,r3,r4
且r1+r2+r3+r4=R,则四个小圆的周长为2π(r1+r2+r3+r4)=2πR=大圆的周长,
故用的材料一样多.
