2020-2021学年人教版八年级数学下册18.1.1平行四边形性质练习(Word版 含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册18.1.1平行四边形性质练习(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 519.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 00:00:00 | ||
图片预览



文档简介
平行四边形性质练习
一、选择题
1.小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是 ( )
?
A.
①,②?????????????B.
①,④?????????????C.
③,④?????????????D.
②,③?????????????
2.
如图,,E在CD延长线上,AB=6,DE=6,EF=9,则BF的长为(???).
?
A.
7?????????????B.
8?????????????C.
9?????????????D.
10?????????????
3.
如图,在平行四边形ABCD中,AD=2AB,CE平分∠BCD交AD边于点E,且AE=3,则AB的长为 ( )
?
A.
4?????????????B.
3?????????????C.
?????????????D.
2?????????????
4.
如图,将等边△ABC沿射线BC向右平移到△DCE的位置,连接AD,BD,则下列结论:
?①AD=BC;②BD,AC互相平分;③四边形ACED是菱形.其中正确的个数是 ( )
?
A.
0?????????????B.
1?????????????C.
2?????????????D.
3?????????????
二、填空题
5.如图,在平行四边形ABCD中,E是AD边上的中点.若∠ABE=∠EBC,AB=2,则平行四边形ABCD的周长是________.
?
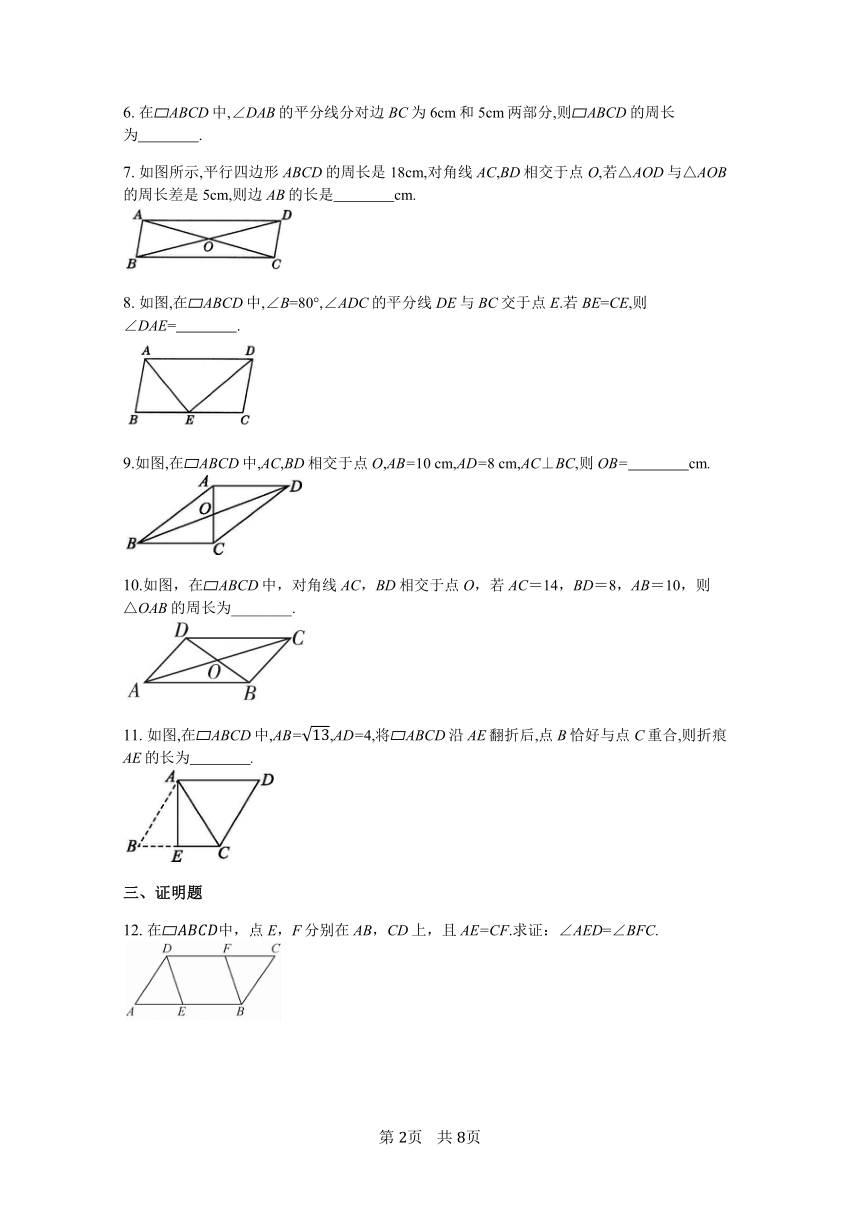
6.
在ABCD中,∠DAB的平分线分对边BC为6cm和5cm两部分,则ABCD的周长为 .?
7.
如图所示,平行四边形ABCD的周长是18cm,对角线AC,BD相交于点O,若△AOD与△AOB的周长差是5cm,则边AB的长是 cm.
?
8.
如图,在ABCD中,∠B=80°,∠ADC的平分线DE与BC交于点E.若BE=CE,则∠DAE= .
?
9.如图,在ABCD中,AC,BD相交于点O,AB=10?cm,AD=8?cm,AC⊥BC,则OB= cm.
?
10.如图,在ABCD中,对角线AC,BD相交于点O,若AC=14,BD=8,AB=10,则△OAB的周长为________.
?
11.
如图,在ABCD中,AB=,AD=4,将ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为 .
?
三、证明题
12.
在中,点E,F分别在AB,CD上,且AE=CF.求证:∠AED=∠BFC.
?
13.
如图,在平行四边形ABCD中,E,F是AC上的两点,若AE?=CF.求证:DE=BF,且DE//BF.
?
14.
如图,四边形ABCD是平行四边形,E,F是对角线BD上的点,∠1=∠2.
?
(1)求证:BE=DF;
(2)求证:AF∥CE.
四、解答题
15.?如图,已知平行四边形ABCD,DE是∠ADC的角平分线,交BC于点E.
?
(1)求证:CD=CE;
(2)若BE=CE,∠B=80°,求∠DAE的度数.
16.
如图,四边形ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.
?
(1)求∠APB的度数;
(2)如果AD=5cm,AP=8cm,求△APB的周长.
17.如图,已知点A(-4,2),B(-1,-2),ABCD的对角线交于坐标原点O.
?
(1)请直接写出点C,D的坐标;
(2)写出从线段AB到线段CD的变换过程;
(3)直接写出ABCD的面积.
参考答案
1.
【答案】D【解析】本题考查了平行四边形的判定.
?∵只有②③两块角的两边互相平行,角的两边的延长线的交点就是平行四边形的顶点,
?∴带②③两块碎玻璃,就可以确定平行四边形的大小.故选D.
2.
【答案】C
3.
【答案】B【解析】根据平行四边形的性质可得AB=DC,AD∥BC,∴∠DEC=∠BCE,∵∠BCE=∠DCE,∴∠DEC=∠DCE,∴DE=DC=AB.又∵AD=2AB,∴AD=2DE,即AE+DE=2DE,∴DE=AE=3,∴AB=3.
4.
【答案】D【解析】由平移的性质,可得△ABC≌△DCE,又因为△ABC是等边三角形且B,C,E三点在同一条直线上,所以∠ACD=60°,又AC=CD,所以△ADC为等边三角形,易证△ABC≌△ADC≌△DCE,所以AD=BC,四边形ABCD是菱形,四边形ACED是菱形.又由四边形ABCD是菱形可得BD,AC互相平分.故①②③均正确.
5.
【答案】12
?【解析】∵平行四边形ABCD,
?∴∠AEB=∠EBC,又∠ABE=∠EBC,
?∴∠ABE=∠AEB,∴AB=AE,∴AD=BC=2AB,
?∴C?ABCD=AB+CD+BC+AD=6AB=6×2=12.
6.
【答案】32?cm或34?cm
?【解析】情况一,如图①,BE=5?cm,CE=6?cm,
?∵四边形ABCD为平行四边形,
?∴AD=BC,AB=CD,AD∥BC,∵∠DAE=∠AEB.
?∵AE平分∠BAD,∴∠BAE=∠DAE,
?∴∠AEB=∠BAE,∴AB=BE=5?cm,
?∴C四边形ABCD=(5+5+6)×?2=32(cm).
?
?情况二,如图②,BE=6?cm,CE=5?cm.
?∵四边形ABCD为平行四边形,
?∴AD=BC,AB=CD,AD∥BC,∴∠DAE=∠AEB.
?∵AE平分∠BAD,∴∠BAE=∠DAE,
?∴∠AEB=∠BAE,∴AB=BE=6?cm,
?∴C四边形ABCD=(6+6+5)×2=34(cm).
7.
【答案】2
?【解析】设AB=xcm,则AD=(5+x)cm,由题意得2(x+5+x)=18,解得x=2,即AB=2cm.
8.
【答案】50°
?【解析】如图所示,过E作EP⊥AD交AD于点P,过E作EM⊥AB交AB于点M,作EN⊥DC交DC的延长线于点N,
?
?则由DE是∠ADC的角平分线,可知EP=EN.由∠EMB=∠ENC=90°,∠MEB=∠NEC,?BE=CE,可证△EMB≌△ENC(AAS),所以EM=EN,所以EM=EP,又EP⊥AD,?EM⊥AB,所以AE是∠BAD的角平分线,故由∠B=80°,可得∠BAD=100°,所以∠DAE=∠BAD=50°.
9.
【答案】
?【解析】本题考查平行四边形的性质和勾股定理,难度中等,先根据平行四边形的性质得出BC=AD=8,再根据勾股定理得出AC=6,进而得出OC=3,利用勾股定理得出OB==.
10.
【答案】21
?【解析】∵ABCD为平行四边形
?∴OA=AC.OB=BD?∴OA=7,OB=4,又AB=10.
?∴C△OAB=7+4+10=21.
11.
【答案】3
?【解析】本题考查图形翻折变换(折叠问题)和平行四边形的性质及勾股定理的知识,难度不大.
?∵四边形ABCD是平行四边形,∴BC=AD=4,又根据题意可知:AB=AC=,BE=CE=BC=2,∠AEB=∠AEC=90°,∴AE====3.故答案为3.
12.
【答案】证明:∵四边形ABCD是平行四边形,
?∴AD=CB,∠A=∠C,
?又AE=CF,
?∴△DAE≌△BCF(SAS),
?∴∠AED=∠BFC.
13.
【答案】证明:∵四边形ABCD是平行四边形,∴AD=?BC,AD//BC,∴.
?又∵AE?=CF,∴△ADE≌△CBF(?SAS),∴DE=BF,,?∴,∴DE//BF.
?
14.
(1)
【答案】∵四边形ABCD是平行四边形,
?∴AB=CD,AB∥CD,∴∠ABE=∠CDF.∴∠1=∠2,(两直线平行,内错角相等)
?∴∠AEB=∠CFD,
?∴△ABE≌△CDF,∴BE=DF.
?(2)
【答案】由第1问得△ABE≌△CDF,∴AE=CF.
?∵∠1=∠2,∴AE∥CF,(内错角相等,两直线平行)
?∴四边形AECF是平行四边形,(一组对边平行且相等的四边形是平行四边形)
?∴AF∥CE.
?
15.
(1)
【答案】如图,在?ABCD中,AD∥BC得,∠1=∠3
?又∠1=∠2,∴∠2=∠3,∴CD=CE(3分)
?
?(2)
【答案】由ABCD得,AB=CD
?又CD=CE,BE=CE
?∴AB=BE?∴∠BAE=∠BEA
?∵∠B=80°,∴∠BAE=50°,
?得:∠DAE=180°-50°-80°=50°.(6分)
?
16.
(1)
【答案】∵四边形ABCD是平行四边形,
?∴AD∥CB,
?∴∠DAB+∠CBA=180°.(两直线平行,同旁内角互补)
?又∵AP和BP分别平分∠DAB和∠CBA,
?∴∠PAB=∠DAB,∠PBA=∠CBA,
?∴∠PAB+∠PBA=×(∠DAB+∠CBA)=90°,
?∴∠APB=180°-(∠PAB+∠PBA)=?180°-90°=90°.
?(2)
【答案】∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,
?∴∠DPA=∠PAB.(两直线平行,内错角相等)
?∵AP平分∠DAB,
?∴∠DAP=∠PAB,∴∠DPA?=∠DAP,
?∴△ADP是等腰三角形,
?∴AD=DP=5?cm,
?同理PC=CB=5?cm,
?∴AB=CD=DP+PC=5?cm+5?cm=10?cm.
?在Rt△APB中,AB=10?cm,AP=8?cm,
?∴BP==6(cm),
?∴△APB的周长是6+8+10=24(cm).
?
17.
(1)
【答案】C(4,-2),D(1,2).
?在平行四边形ABCD中,由于对角线的交点恰好与坐标原点重合,所以A与C和B与D关于原点对称,所以C(4,-2),D(1,2);
?(2)
【答案】从线段AB到线段CD,可以看作是将线段AB绕O点旋转180°得到的.??
?因为平行四边形是中心对称图形,所以线段AB绕原点O旋转180°后得到线段CD;
?(3)
【答案】20.
?由ABCD四点的坐标可知:BC=4-(-1)=5,BC边上的高为4,所以?ABCD的面积为20.
?
第6页
共8页
第5页
共8页
一、选择题
1.小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是 ( )
?
A.
①,②?????????????B.
①,④?????????????C.
③,④?????????????D.
②,③?????????????
2.
如图,,E在CD延长线上,AB=6,DE=6,EF=9,则BF的长为(???).
?
A.
7?????????????B.
8?????????????C.
9?????????????D.
10?????????????
3.
如图,在平行四边形ABCD中,AD=2AB,CE平分∠BCD交AD边于点E,且AE=3,则AB的长为 ( )
?
A.
4?????????????B.
3?????????????C.
?????????????D.
2?????????????
4.
如图,将等边△ABC沿射线BC向右平移到△DCE的位置,连接AD,BD,则下列结论:
?①AD=BC;②BD,AC互相平分;③四边形ACED是菱形.其中正确的个数是 ( )
?
A.
0?????????????B.
1?????????????C.
2?????????????D.
3?????????????
二、填空题
5.如图,在平行四边形ABCD中,E是AD边上的中点.若∠ABE=∠EBC,AB=2,则平行四边形ABCD的周长是________.
?
6.
在ABCD中,∠DAB的平分线分对边BC为6cm和5cm两部分,则ABCD的周长为 .?
7.
如图所示,平行四边形ABCD的周长是18cm,对角线AC,BD相交于点O,若△AOD与△AOB的周长差是5cm,则边AB的长是 cm.
?
8.
如图,在ABCD中,∠B=80°,∠ADC的平分线DE与BC交于点E.若BE=CE,则∠DAE= .
?
9.如图,在ABCD中,AC,BD相交于点O,AB=10?cm,AD=8?cm,AC⊥BC,则OB= cm.
?
10.如图,在ABCD中,对角线AC,BD相交于点O,若AC=14,BD=8,AB=10,则△OAB的周长为________.
?
11.
如图,在ABCD中,AB=,AD=4,将ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为 .
?
三、证明题
12.
在中,点E,F分别在AB,CD上,且AE=CF.求证:∠AED=∠BFC.
?
13.
如图,在平行四边形ABCD中,E,F是AC上的两点,若AE?=CF.求证:DE=BF,且DE//BF.
?
14.
如图,四边形ABCD是平行四边形,E,F是对角线BD上的点,∠1=∠2.
?
(1)求证:BE=DF;
(2)求证:AF∥CE.
四、解答题
15.?如图,已知平行四边形ABCD,DE是∠ADC的角平分线,交BC于点E.
?
(1)求证:CD=CE;
(2)若BE=CE,∠B=80°,求∠DAE的度数.
16.
如图,四边形ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.
?
(1)求∠APB的度数;
(2)如果AD=5cm,AP=8cm,求△APB的周长.
17.如图,已知点A(-4,2),B(-1,-2),ABCD的对角线交于坐标原点O.
?
(1)请直接写出点C,D的坐标;
(2)写出从线段AB到线段CD的变换过程;
(3)直接写出ABCD的面积.
参考答案
1.
【答案】D【解析】本题考查了平行四边形的判定.
?∵只有②③两块角的两边互相平行,角的两边的延长线的交点就是平行四边形的顶点,
?∴带②③两块碎玻璃,就可以确定平行四边形的大小.故选D.
2.
【答案】C
3.
【答案】B【解析】根据平行四边形的性质可得AB=DC,AD∥BC,∴∠DEC=∠BCE,∵∠BCE=∠DCE,∴∠DEC=∠DCE,∴DE=DC=AB.又∵AD=2AB,∴AD=2DE,即AE+DE=2DE,∴DE=AE=3,∴AB=3.
4.
【答案】D【解析】由平移的性质,可得△ABC≌△DCE,又因为△ABC是等边三角形且B,C,E三点在同一条直线上,所以∠ACD=60°,又AC=CD,所以△ADC为等边三角形,易证△ABC≌△ADC≌△DCE,所以AD=BC,四边形ABCD是菱形,四边形ACED是菱形.又由四边形ABCD是菱形可得BD,AC互相平分.故①②③均正确.
5.
【答案】12
?【解析】∵平行四边形ABCD,
?∴∠AEB=∠EBC,又∠ABE=∠EBC,
?∴∠ABE=∠AEB,∴AB=AE,∴AD=BC=2AB,
?∴C?ABCD=AB+CD+BC+AD=6AB=6×2=12.
6.
【答案】32?cm或34?cm
?【解析】情况一,如图①,BE=5?cm,CE=6?cm,
?∵四边形ABCD为平行四边形,
?∴AD=BC,AB=CD,AD∥BC,∵∠DAE=∠AEB.
?∵AE平分∠BAD,∴∠BAE=∠DAE,
?∴∠AEB=∠BAE,∴AB=BE=5?cm,
?∴C四边形ABCD=(5+5+6)×?2=32(cm).
?
?情况二,如图②,BE=6?cm,CE=5?cm.
?∵四边形ABCD为平行四边形,
?∴AD=BC,AB=CD,AD∥BC,∴∠DAE=∠AEB.
?∵AE平分∠BAD,∴∠BAE=∠DAE,
?∴∠AEB=∠BAE,∴AB=BE=6?cm,
?∴C四边形ABCD=(6+6+5)×2=34(cm).
7.
【答案】2
?【解析】设AB=xcm,则AD=(5+x)cm,由题意得2(x+5+x)=18,解得x=2,即AB=2cm.
8.
【答案】50°
?【解析】如图所示,过E作EP⊥AD交AD于点P,过E作EM⊥AB交AB于点M,作EN⊥DC交DC的延长线于点N,
?
?则由DE是∠ADC的角平分线,可知EP=EN.由∠EMB=∠ENC=90°,∠MEB=∠NEC,?BE=CE,可证△EMB≌△ENC(AAS),所以EM=EN,所以EM=EP,又EP⊥AD,?EM⊥AB,所以AE是∠BAD的角平分线,故由∠B=80°,可得∠BAD=100°,所以∠DAE=∠BAD=50°.
9.
【答案】
?【解析】本题考查平行四边形的性质和勾股定理,难度中等,先根据平行四边形的性质得出BC=AD=8,再根据勾股定理得出AC=6,进而得出OC=3,利用勾股定理得出OB==.
10.
【答案】21
?【解析】∵ABCD为平行四边形
?∴OA=AC.OB=BD?∴OA=7,OB=4,又AB=10.
?∴C△OAB=7+4+10=21.
11.
【答案】3
?【解析】本题考查图形翻折变换(折叠问题)和平行四边形的性质及勾股定理的知识,难度不大.
?∵四边形ABCD是平行四边形,∴BC=AD=4,又根据题意可知:AB=AC=,BE=CE=BC=2,∠AEB=∠AEC=90°,∴AE====3.故答案为3.
12.
【答案】证明:∵四边形ABCD是平行四边形,
?∴AD=CB,∠A=∠C,
?又AE=CF,
?∴△DAE≌△BCF(SAS),
?∴∠AED=∠BFC.
13.
【答案】证明:∵四边形ABCD是平行四边形,∴AD=?BC,AD//BC,∴.
?又∵AE?=CF,∴△ADE≌△CBF(?SAS),∴DE=BF,,?∴,∴DE//BF.
?
14.
(1)
【答案】∵四边形ABCD是平行四边形,
?∴AB=CD,AB∥CD,∴∠ABE=∠CDF.∴∠1=∠2,(两直线平行,内错角相等)
?∴∠AEB=∠CFD,
?∴△ABE≌△CDF,∴BE=DF.
?(2)
【答案】由第1问得△ABE≌△CDF,∴AE=CF.
?∵∠1=∠2,∴AE∥CF,(内错角相等,两直线平行)
?∴四边形AECF是平行四边形,(一组对边平行且相等的四边形是平行四边形)
?∴AF∥CE.
?
15.
(1)
【答案】如图,在?ABCD中,AD∥BC得,∠1=∠3
?又∠1=∠2,∴∠2=∠3,∴CD=CE(3分)
?
?(2)
【答案】由ABCD得,AB=CD
?又CD=CE,BE=CE
?∴AB=BE?∴∠BAE=∠BEA
?∵∠B=80°,∴∠BAE=50°,
?得:∠DAE=180°-50°-80°=50°.(6分)
?
16.
(1)
【答案】∵四边形ABCD是平行四边形,
?∴AD∥CB,
?∴∠DAB+∠CBA=180°.(两直线平行,同旁内角互补)
?又∵AP和BP分别平分∠DAB和∠CBA,
?∴∠PAB=∠DAB,∠PBA=∠CBA,
?∴∠PAB+∠PBA=×(∠DAB+∠CBA)=90°,
?∴∠APB=180°-(∠PAB+∠PBA)=?180°-90°=90°.
?(2)
【答案】∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,
?∴∠DPA=∠PAB.(两直线平行,内错角相等)
?∵AP平分∠DAB,
?∴∠DAP=∠PAB,∴∠DPA?=∠DAP,
?∴△ADP是等腰三角形,
?∴AD=DP=5?cm,
?同理PC=CB=5?cm,
?∴AB=CD=DP+PC=5?cm+5?cm=10?cm.
?在Rt△APB中,AB=10?cm,AP=8?cm,
?∴BP==6(cm),
?∴△APB的周长是6+8+10=24(cm).
?
17.
(1)
【答案】C(4,-2),D(1,2).
?在平行四边形ABCD中,由于对角线的交点恰好与坐标原点重合,所以A与C和B与D关于原点对称,所以C(4,-2),D(1,2);
?(2)
【答案】从线段AB到线段CD,可以看作是将线段AB绕O点旋转180°得到的.??
?因为平行四边形是中心对称图形,所以线段AB绕原点O旋转180°后得到线段CD;
?(3)
【答案】20.
?由ABCD四点的坐标可知:BC=4-(-1)=5,BC边上的高为4,所以?ABCD的面积为20.
?
第6页
共8页
第5页
共8页
