2020-2021学年人教版八年级数学下册 18.1.1 平行四边形的性质 课后练习(Word版 含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册 18.1.1 平行四边形的性质 课后练习(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 374.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 00:00:00 | ||
图片预览

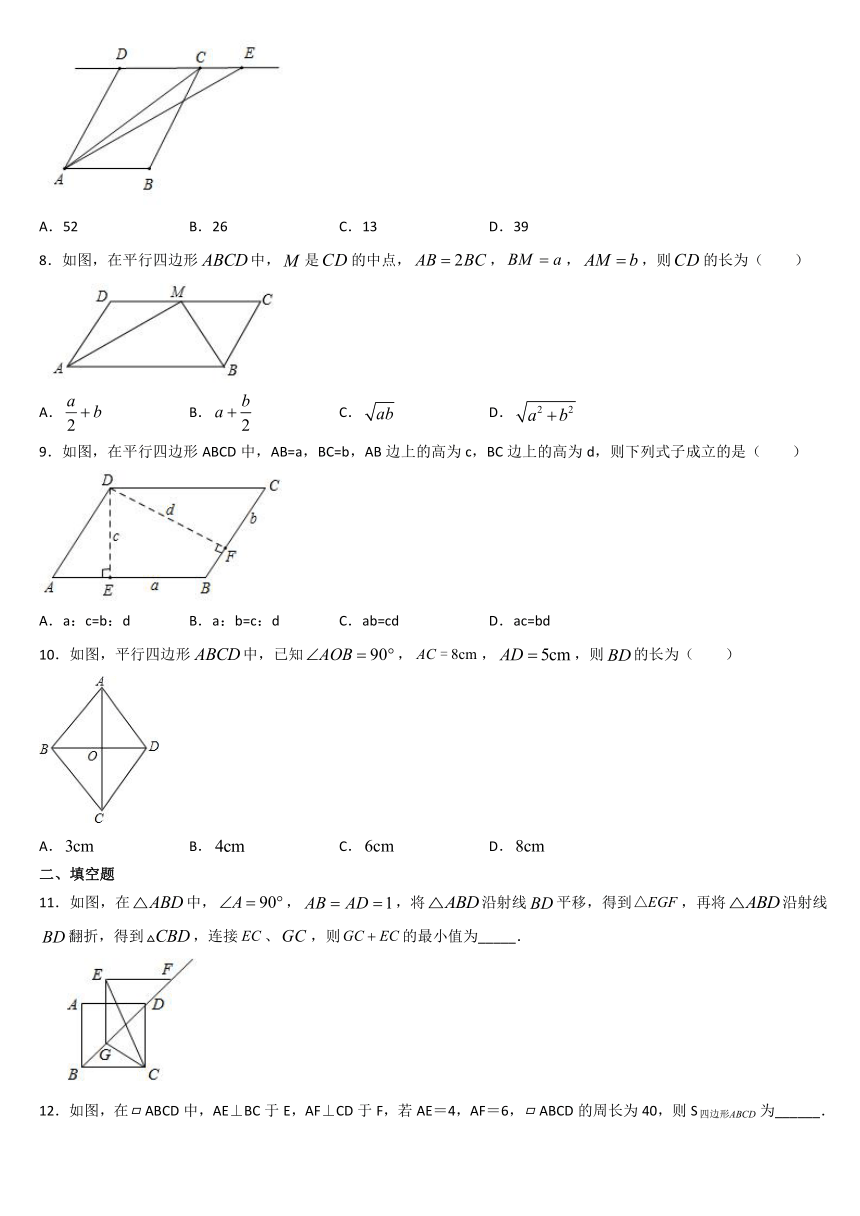

文档简介
人教版八年级数学下册
第十八章
平行四边形
18.1.1
平行四边形的性质
课后练习
一、选择题
1.平行四边形一边的长是,则这个平行四边形的两条对角线长可以是(
)
A.或
B.或
C.或
D.或
2.平行四边形的一边长是10cm,那么它的两条对角线的长可以是(
)
A.4cm和6cm
B.6cm和8cm
C.8cm和10cm
D.10cm和12cm
3.如图,在□ABCD中AE⊥BC,垂足为E,AF⊥CD,垂足为F,若AE:AF=2:3,□ABCD的周长为40,则AB的长为(
)
A.8
B.9
C.12
D.15
4.如图,平行四边形ABCD的对角线AC,BD相交于点O,则下列结论不一定成立的是(
)
A.AB//CD
B.AD=BC
C.OA=OC
D.∠ABD=∠CBD
5.如图所示,在平行四边形ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于(
)
A.2
cm
B.3
cm
C.4
cm
D.5
cm
6.如图1,平行四边形纸片的面积为120,.今沿两对角线将四边形剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(、重合)形成一轴对称图形(戊),如图2所示,则图形戊的两对角线长度和为(
)
A.26
B.29
C.
D.
7.如图,是直线上的一点,且.已知的面积为,则的面积为(
)
A.52
B.26
C.13
D.39
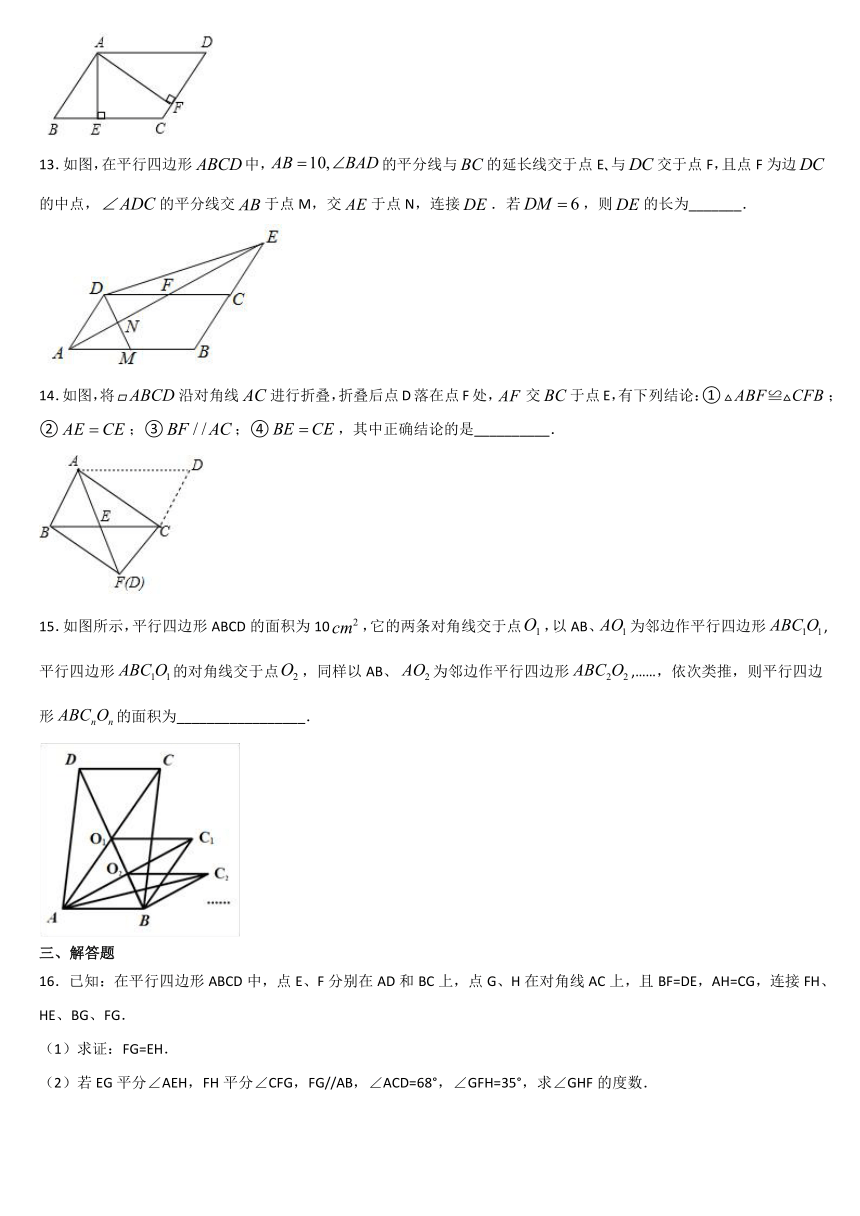
8.如图,在平行四边形中,是的中点,,,,则的长为(
)
A.
B.
C.
D.
9.如图,在平行四边形ABCD中,AB=a,BC=b,AB边上的高为c,BC边上的高为d,则下列式子成立的是(
)
A.a:c=b:d
B.a:b=c:d
C.ab=cd
D.ac=bd
10.如图,平行四边形中,已知,,,则的长为(
)
A.
B.
C.
D.
二、填空题
11.如图,在中,,,将沿射线平移,得到,再将沿射线翻折,得到,连接、,则的最小值为_____.
12.如图,在ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=4,AF=6,ABCD的周长为40,则S为______.
13.如图,在平行四边形中,的平分线与的延长线交于点E?与交于点F,且点F为边的中点,的平分线交于点M,交于点N,连接.若,则的长为_______.
14.如图,将沿对角线进行折叠,折叠后点D落在点F处,交于点E,有下列结论:①;②;③;④,其中正确结论的是__________.
15.如图所示,平行四边形ABCD的面积为10,它的两条对角线交于点,以AB、为邻边作平行四边形,平行四边形的对角线交于点,同样以AB、为邻边作平行四边形,……,依次类推,则平行四边形的面积为_________________.
三、解答题
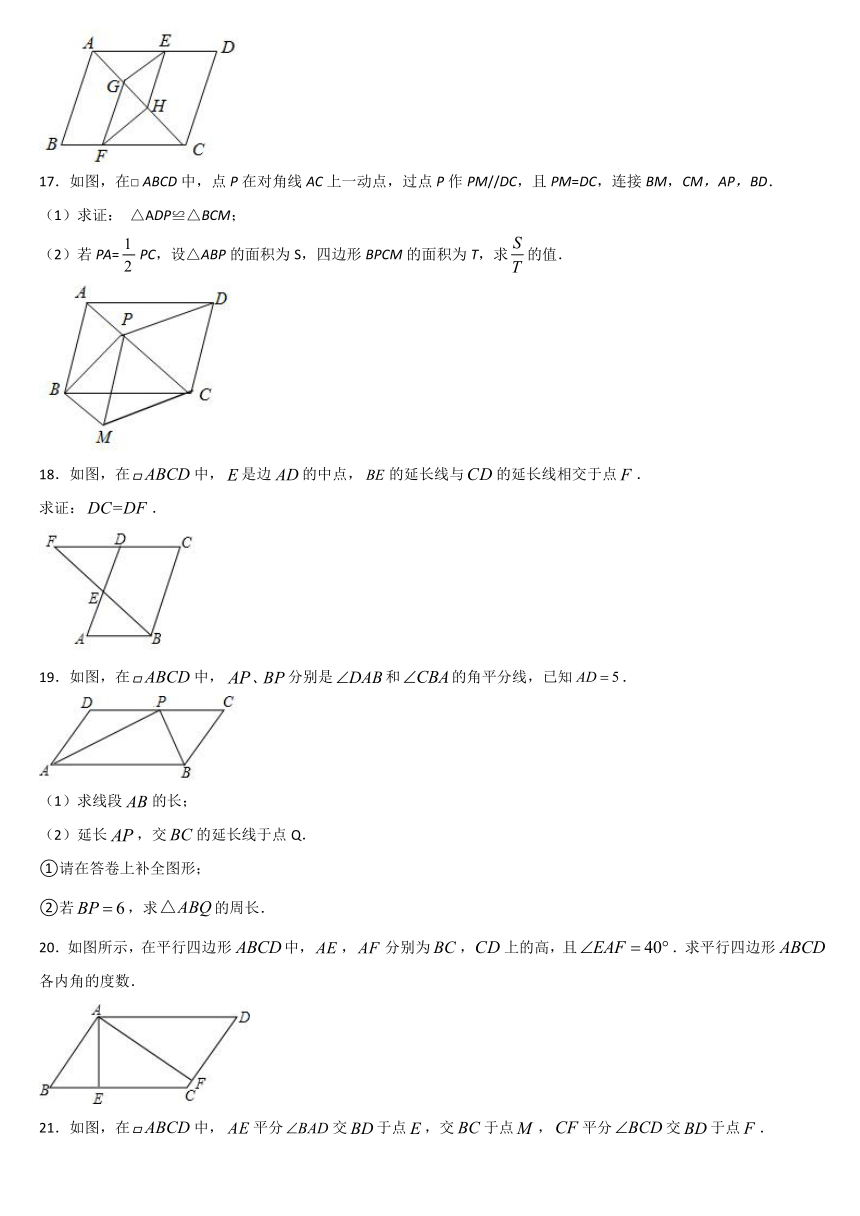
16.已知:在平行四边形ABCD中,点E、F分别在AD和BC上,点G、H在对角线AC上,且BF=DE,AH=CG,连接FH、HE、BG、FG.
(1)求证:FG=EH.
(2)若EG平分∠AEH,FH平分∠CFG,FG//AB,∠ACD=68°,∠GFH=35°,求∠GHF的度数.
17.如图,在□
ABCD中,点P在对角线AC上一动点,过点P作PM//DC,且PM=DC,连接BM,CM,AP,BD.
(1)求证:
△ADP≌△BCM;
(2)若PA=PC,设△ABP的面积为S,四边形BPCM的面积为T,求的值.
18.如图,在中,是边的中点,的延长线与的延长线相交于点.
求证:.
19.如图,在中,?分别是和的角平分线,已知.
(1)求线段的长;
(2)延长,交的延长线于点Q.
①请在答卷上补全图形;
②若,求的周长.
20.如图所示,在平行四边形中,,分别为,上的高,且.求平行四边形各内角的度数.
21.如图,在中,平分交于点,交于点,平分交于点.
(1)若,求的度数;
(2)求证:.
22.如图,已知?ABCD的对角线AC、BD相交于点O,AD=12,BD=10,AC=26.
(1)求△ADO的周长;
(2)求证:△ADO是直角三角形.
23.下面是小明设计的“作平行四边形的高”的尺规作图过程
已知:平行四边形ABCD.
求作:,垂足为点E.
作法:如图,
①分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于P,Q两点;
②作直线PQ,交AB于点O;
③以点O为圆心,OA长为半径做圆,交线段BC于点E;
④连接AE.
所以线段AE就是所求作的高.
根据小明设计的尺规作图过程
⑴使用直尺和圆规,补全图形;(保留作图痕迹)
⑵完成下面的证明
证明:AP=BP,
AQ=
,
PQ为线段AB的垂直平分线.
O为AB中点.
AB为直径,⊙O与线段BC交于点E,
.(
)(填推理的依据)
.
【参考答案】
1.D
2.D
3.A
4.D
5.A
6.A
7.C
8.D
9.D
10.C
11.
12.48
13.
14.①②③
15.
16.解:(1)∵四边形ABCD是平行四边形,
∴,,
∴,
∵,
∴,即,
在和中,
,
∴≌,
∴FG=EH;
(2)∵FH平分∠CFG,∠GFH=35°,
∴,
∵FG//AB,
∴,
∵四边形ABCD是平行四边形,
∴,
∴,
∴.
17.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠ADC+∠BCD=,
∵PM//DC,且PM=DC,
∴四边形PMCD是平行四边形,
∴PD=CM,∠PDC+∠DCM=,
∴∠ADP=∠BCM,
∴△ADP≌△BCM;
(2)解:作BH⊥AC于H,DG⊥AC于G,
∵四边形ABCD是平行四边形,
∴△ABC≌△CDA,
∴BH=DG,
∴,即,
,即,
∵△ADP≌△BCM,
∴,
∴=.
18.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=DC,
∴∠F=∠EBA,
∵E是AD边的中点,
∴DE=AE,
在△DEF和△AEB中,
,
∴△DEF≌△AEB(AAS),
∴DF=AB,
∴DC=DF.
19.解:(1)∵在□ABCD中,AD=5,
∴BC=5,
∵AB∥CD,
∴∠BAP=∠DPA,
∵AP平分∠BAD,
∴∠BAP=∠DAP,
∴∠DAP=∠DPA,
∴DP=AD=5,
同理可得,CP=BC=5,
∴CD=10,
∴AB=10;
(2)①如图所示:
②∵AD∥BQ,
∴∠Q=∠DAP,
又∵∠DAP=∠BAP,
∴∠Q=∠BAP,
∴AB=QB=10,
又∵BP平分∠ABQ,
∴BP⊥AQ,AP=QP,
∴Rt△ABP中,AP==8,
∴AQ=16,
∴△ABQ的周长为:16+10+10=36.
20.解:∵AE、AF分别为BC、CD上的高,
∴∠AEC=∠AFC=90°,
∵∠EAF=40°,
∴∠C=360°-∠EAF-∠AEC-∠AFC=140°,
∵四边形ABCD是平行四边形,
∴∠BAD=∠C=140°,∠B=∠D=180°-∠C=40°.
∴平行四边形ABCD各内角的度数分别为:140°,40°,140°,40°.
21.(1)解:∵四边形是平行四边形,
∴,
∴
.
∵,
∴.
∵平分,
∴.
∵,
∴.
(2)证明:∵四边形是平行四边形,
∴,,,
∴
.
∵平分,
∴.
∵平分,
∴.
∵,
∴.
又∵,,
∴,
∴.
22.解:(1)∵四边形ABCD是平行四边形,
∴对角线AC与BD相互平分,
∴OA=OC=AC,OB=OD=BD,
∵AC=26,BD=10,
∴OA=13,OD=5,
∵AD=12,
∴△AOD的周长=5+12+13=30;
(2)由(1)知
OA=13,OD=5,AD=12,
∵52+
122=132
,
∴在△AOD中,AD2+DO2=AO2
,
∴△AOD是直角三角形.
23.(1)如下图,
(2)BQ,
90°(直径所对的圆周角是直角)
第十八章
平行四边形
18.1.1
平行四边形的性质
课后练习
一、选择题
1.平行四边形一边的长是,则这个平行四边形的两条对角线长可以是(
)
A.或
B.或
C.或
D.或
2.平行四边形的一边长是10cm,那么它的两条对角线的长可以是(
)
A.4cm和6cm
B.6cm和8cm
C.8cm和10cm
D.10cm和12cm
3.如图,在□ABCD中AE⊥BC,垂足为E,AF⊥CD,垂足为F,若AE:AF=2:3,□ABCD的周长为40,则AB的长为(
)
A.8
B.9
C.12
D.15
4.如图,平行四边形ABCD的对角线AC,BD相交于点O,则下列结论不一定成立的是(
)
A.AB//CD
B.AD=BC
C.OA=OC
D.∠ABD=∠CBD
5.如图所示,在平行四边形ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于(
)
A.2
cm
B.3
cm
C.4
cm
D.5
cm
6.如图1,平行四边形纸片的面积为120,.今沿两对角线将四边形剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(、重合)形成一轴对称图形(戊),如图2所示,则图形戊的两对角线长度和为(
)
A.26
B.29
C.
D.
7.如图,是直线上的一点,且.已知的面积为,则的面积为(
)
A.52
B.26
C.13
D.39
8.如图,在平行四边形中,是的中点,,,,则的长为(
)
A.
B.
C.
D.
9.如图,在平行四边形ABCD中,AB=a,BC=b,AB边上的高为c,BC边上的高为d,则下列式子成立的是(
)
A.a:c=b:d
B.a:b=c:d
C.ab=cd
D.ac=bd
10.如图,平行四边形中,已知,,,则的长为(
)
A.
B.
C.
D.
二、填空题
11.如图,在中,,,将沿射线平移,得到,再将沿射线翻折,得到,连接、,则的最小值为_____.
12.如图,在ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=4,AF=6,ABCD的周长为40,则S为______.
13.如图,在平行四边形中,的平分线与的延长线交于点E?与交于点F,且点F为边的中点,的平分线交于点M,交于点N,连接.若,则的长为_______.
14.如图,将沿对角线进行折叠,折叠后点D落在点F处,交于点E,有下列结论:①;②;③;④,其中正确结论的是__________.
15.如图所示,平行四边形ABCD的面积为10,它的两条对角线交于点,以AB、为邻边作平行四边形,平行四边形的对角线交于点,同样以AB、为邻边作平行四边形,……,依次类推,则平行四边形的面积为_________________.
三、解答题
16.已知:在平行四边形ABCD中,点E、F分别在AD和BC上,点G、H在对角线AC上,且BF=DE,AH=CG,连接FH、HE、BG、FG.
(1)求证:FG=EH.
(2)若EG平分∠AEH,FH平分∠CFG,FG//AB,∠ACD=68°,∠GFH=35°,求∠GHF的度数.
17.如图,在□
ABCD中,点P在对角线AC上一动点,过点P作PM//DC,且PM=DC,连接BM,CM,AP,BD.
(1)求证:
△ADP≌△BCM;
(2)若PA=PC,设△ABP的面积为S,四边形BPCM的面积为T,求的值.
18.如图,在中,是边的中点,的延长线与的延长线相交于点.
求证:.
19.如图,在中,?分别是和的角平分线,已知.
(1)求线段的长;
(2)延长,交的延长线于点Q.
①请在答卷上补全图形;
②若,求的周长.
20.如图所示,在平行四边形中,,分别为,上的高,且.求平行四边形各内角的度数.
21.如图,在中,平分交于点,交于点,平分交于点.
(1)若,求的度数;
(2)求证:.
22.如图,已知?ABCD的对角线AC、BD相交于点O,AD=12,BD=10,AC=26.
(1)求△ADO的周长;
(2)求证:△ADO是直角三角形.
23.下面是小明设计的“作平行四边形的高”的尺规作图过程
已知:平行四边形ABCD.
求作:,垂足为点E.
作法:如图,
①分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于P,Q两点;
②作直线PQ,交AB于点O;
③以点O为圆心,OA长为半径做圆,交线段BC于点E;
④连接AE.
所以线段AE就是所求作的高.
根据小明设计的尺规作图过程
⑴使用直尺和圆规,补全图形;(保留作图痕迹)
⑵完成下面的证明
证明:AP=BP,
AQ=
,
PQ为线段AB的垂直平分线.
O为AB中点.
AB为直径,⊙O与线段BC交于点E,
.(
)(填推理的依据)
.
【参考答案】
1.D
2.D
3.A
4.D
5.A
6.A
7.C
8.D
9.D
10.C
11.
12.48
13.
14.①②③
15.
16.解:(1)∵四边形ABCD是平行四边形,
∴,,
∴,
∵,
∴,即,
在和中,
,
∴≌,
∴FG=EH;
(2)∵FH平分∠CFG,∠GFH=35°,
∴,
∵FG//AB,
∴,
∵四边形ABCD是平行四边形,
∴,
∴,
∴.
17.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠ADC+∠BCD=,
∵PM//DC,且PM=DC,
∴四边形PMCD是平行四边形,
∴PD=CM,∠PDC+∠DCM=,
∴∠ADP=∠BCM,
∴△ADP≌△BCM;
(2)解:作BH⊥AC于H,DG⊥AC于G,
∵四边形ABCD是平行四边形,
∴△ABC≌△CDA,
∴BH=DG,
∴,即,
,即,
∵△ADP≌△BCM,
∴,
∴=.
18.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=DC,
∴∠F=∠EBA,
∵E是AD边的中点,
∴DE=AE,
在△DEF和△AEB中,
,
∴△DEF≌△AEB(AAS),
∴DF=AB,
∴DC=DF.
19.解:(1)∵在□ABCD中,AD=5,
∴BC=5,
∵AB∥CD,
∴∠BAP=∠DPA,
∵AP平分∠BAD,
∴∠BAP=∠DAP,
∴∠DAP=∠DPA,
∴DP=AD=5,
同理可得,CP=BC=5,
∴CD=10,
∴AB=10;
(2)①如图所示:
②∵AD∥BQ,
∴∠Q=∠DAP,
又∵∠DAP=∠BAP,
∴∠Q=∠BAP,
∴AB=QB=10,
又∵BP平分∠ABQ,
∴BP⊥AQ,AP=QP,
∴Rt△ABP中,AP==8,
∴AQ=16,
∴△ABQ的周长为:16+10+10=36.
20.解:∵AE、AF分别为BC、CD上的高,
∴∠AEC=∠AFC=90°,
∵∠EAF=40°,
∴∠C=360°-∠EAF-∠AEC-∠AFC=140°,
∵四边形ABCD是平行四边形,
∴∠BAD=∠C=140°,∠B=∠D=180°-∠C=40°.
∴平行四边形ABCD各内角的度数分别为:140°,40°,140°,40°.
21.(1)解:∵四边形是平行四边形,
∴,
∴
.
∵,
∴.
∵平分,
∴.
∵,
∴.
(2)证明:∵四边形是平行四边形,
∴,,,
∴
.
∵平分,
∴.
∵平分,
∴.
∵,
∴.
又∵,,
∴,
∴.
22.解:(1)∵四边形ABCD是平行四边形,
∴对角线AC与BD相互平分,
∴OA=OC=AC,OB=OD=BD,
∵AC=26,BD=10,
∴OA=13,OD=5,
∵AD=12,
∴△AOD的周长=5+12+13=30;
(2)由(1)知
OA=13,OD=5,AD=12,
∵52+
122=132
,
∴在△AOD中,AD2+DO2=AO2
,
∴△AOD是直角三角形.
23.(1)如下图,
(2)BQ,
90°(直径所对的圆周角是直角)
