2020-2021学年华东师大版八年级数学下册18.2.1平行四边形的判定定理1、2 复习练习题(Word版,附答案)
文档属性
| 名称 | 2020-2021学年华东师大版八年级数学下册18.2.1平行四边形的判定定理1、2 复习练习题(Word版,附答案) |  | |
| 格式 | doc | ||
| 文件大小 | 106.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 11:28:56 | ||
图片预览

文档简介
第18章 平行四边形 18.2.1 平行四边形的判定定理1、2
1.四边形中,有两条边相等,另两条边也相等,则这个四边形( )
A.一定是平行四边形 B.一定不是平行四边形
C.可能是平行四边形 D.上述答案都不对
2.在四边形ABCD中,AD∥BC,要判别四边形ABCD是平行四边形,还需满足( )
A.∠A+∠C=180° B.∠B+∠D=180°
C.∠A+∠B=180° D.∠A+∠D=180°
3.如图,在平面直角坐标系中,以O(0,0)、A(1,1)、B(3,0)为顶点构造平行四边形,下列各点中,不能作为平行四边形顶点坐标的是( )
A.(-3,1) B.(4,1) C.(-2,1) D.(2,-1)
4. 下列两个图形,一定可以组成平行四边形的是( )
A.两个等腰三角形 B.两个直角三角形
C.两个锐角三角形 D.两个全等三角形
5.如图,下列四组条件中,不能判定四边形ABCD是平行四边形的是( )
A.AB=DC,AD=BC B.AB∥CD,AD∥BC
C.AB∥DC,AD=BC D.AB∥DC,AB=DC
6.点A、B、C、D在同一平面内,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD中任选两个条件,不能使四边形ABCD是平行四边形的组合是( )
A.①② B.②③ C. ①③ D.③④
7.已知四边形ABCD,从①AB∥CD;②AD∥BC;③AB=CD;④AD=BC;⑤AD=DC;⑥CB=CD六个条件中任取两个,能推出四边形ABCD是平行四边形的取法共有( )
A.6种 B.5种 C. 4种 D.3种
8.下面给出的条件中,能判定四边形ABCD为平行四边形的是( )
A.AB∥CD,AD=BC B.AB=CD,AD=BC
C.AB=AD,CB=CD D.∠B=∠C,∠A=∠D
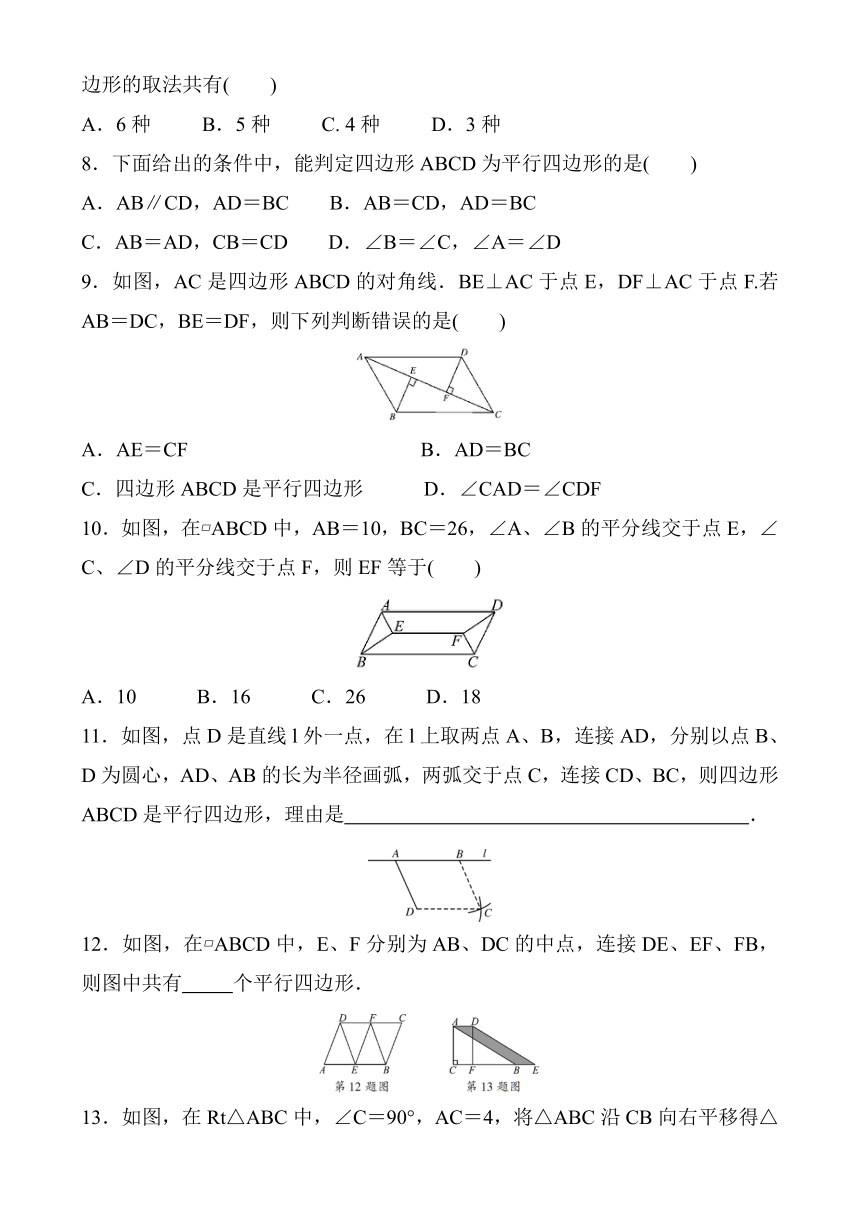
9.如图,AC是四边形ABCD的对角线.BE⊥AC于点E,DF⊥AC于点F.若AB=DC,BE=DF,则下列判断错误的是( )
A.AE=CF B.AD=BC
C.四边形ABCD是平行四边形 D.∠CAD=∠CDF
10.如图,在?ABCD中,AB=10,BC=26,∠A、∠B的平分线交于点E,∠C、∠D的平分线交于点F,则EF等于( )
A.10 B.16 C.26 D.18
11.如图,点D是直线l外一点,在l上取两点A、B,连接AD,分别以点B、D为圆心,AD、AB的长为半径画弧,两弧交于点C,连接CD、BC,则四边形ABCD是平行四边形,理由是 .
12.如图,在?ABCD中,E、F分别为AB、DC的中点,连接DE、EF、FB,则图中共有 个平行四边形.
13.如图,在Rt△ABC中,∠C=90°,AC=4,将△ABC沿CB向右平移得△DEF,若平移距离为2,则四边形ABED的面积等于 .
14. 如图,在四边形ABCD中,AB=CD,E、F在对角线AC上,且DE∥BF,AD∥BC,AE=CF,求证:四边形ABCD为平行四边形.
如图所示,已知在?ABCD中,AM=CN,求证:四边形MBND是平行四边形.
如图所示,已知AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,且AE=DF.求证四边形BECF是平行四边形.
17.如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.求证:
(1)AC=EF;
(2)四边形ADFE是平行四边形.
18.如图,△ABD、△ACE、△BCF分别是以△ABC的AB、AC、BC为边的等边三角形.求证:四边形ADFE是平行四边形.
答案:
1-10 CDADC BCBDB
11. 两组对边分别相等的四边形是平行四边形
12. 4
13. 8
14. 证明:∵DE∥BF,∴∠DEF=∠BFE,∴∠3=∠4.又AD∥BC,∴∠1=∠2.又AE=CF,∴△ADE≌△CBF,∴AD=BC,又AB=CD.∴四边形ABCD为平行四边形.
15. 证明:∵四边形ABCD是平行四边形,∴AB∥CD,且AB=CD,又AM=CN,∴BM綊DN,∴四边形MBND是平行四边形(一组对边平行且相等的四边形是平行四边形).
16. 证明:∵BE⊥AD,CF⊥AD,∴∠AEB=∠DFC=90°,∵AB∥CD,∴∠A=∠D,在△AEB和△DFC中,∠AEB=∠DFC,AE=DF,∠A=∠D,∴△AEB≌△DFC,∴BE=CF,∵BE⊥AD,CF⊥AD,∴BE∥CF,∴四边形BECF是平行四边形.
17. 证明:(1)在Rt△ABC中,∵∠BAC=30°,∴AB=2BC.∵△ABE是等边三角形,EF⊥AB,∴AB=2AF.∴AF=BC.在Rt△AFE和Rt△BCA中,∵,∴△AFE≌△BCA(HL),∴AC=EF;
(2)∵△ACD是等边三角形,∴∠DAC=60°,AC=AD,∴∠DAB=∠DAC+∠BAC=90°,∴AD⊥AB.又∵EF⊥AB,∴EF∥AD.∵AC=EF,AC=AD,∴EF=AD.∴四边形ADFE是平行四边形.
18. 证明:∵△ACE、△BCF都是等边三角形,∴CF=CB=BF,CA=CE=AE,∠ACE=∠FCB=60°,∴∠FCE=∠ACB,∴△FCE≌△BCA,∴EF=AB,∵AB=AD,∴AD=EF,同理可证AE=DF,∴四边形ADFE是平行四边形.
1.四边形中,有两条边相等,另两条边也相等,则这个四边形( )
A.一定是平行四边形 B.一定不是平行四边形
C.可能是平行四边形 D.上述答案都不对
2.在四边形ABCD中,AD∥BC,要判别四边形ABCD是平行四边形,还需满足( )
A.∠A+∠C=180° B.∠B+∠D=180°
C.∠A+∠B=180° D.∠A+∠D=180°
3.如图,在平面直角坐标系中,以O(0,0)、A(1,1)、B(3,0)为顶点构造平行四边形,下列各点中,不能作为平行四边形顶点坐标的是( )
A.(-3,1) B.(4,1) C.(-2,1) D.(2,-1)
4. 下列两个图形,一定可以组成平行四边形的是( )
A.两个等腰三角形 B.两个直角三角形
C.两个锐角三角形 D.两个全等三角形
5.如图,下列四组条件中,不能判定四边形ABCD是平行四边形的是( )
A.AB=DC,AD=BC B.AB∥CD,AD∥BC
C.AB∥DC,AD=BC D.AB∥DC,AB=DC
6.点A、B、C、D在同一平面内,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD中任选两个条件,不能使四边形ABCD是平行四边形的组合是( )
A.①② B.②③ C. ①③ D.③④
7.已知四边形ABCD,从①AB∥CD;②AD∥BC;③AB=CD;④AD=BC;⑤AD=DC;⑥CB=CD六个条件中任取两个,能推出四边形ABCD是平行四边形的取法共有( )
A.6种 B.5种 C. 4种 D.3种
8.下面给出的条件中,能判定四边形ABCD为平行四边形的是( )
A.AB∥CD,AD=BC B.AB=CD,AD=BC
C.AB=AD,CB=CD D.∠B=∠C,∠A=∠D
9.如图,AC是四边形ABCD的对角线.BE⊥AC于点E,DF⊥AC于点F.若AB=DC,BE=DF,则下列判断错误的是( )
A.AE=CF B.AD=BC
C.四边形ABCD是平行四边形 D.∠CAD=∠CDF
10.如图,在?ABCD中,AB=10,BC=26,∠A、∠B的平分线交于点E,∠C、∠D的平分线交于点F,则EF等于( )
A.10 B.16 C.26 D.18
11.如图,点D是直线l外一点,在l上取两点A、B,连接AD,分别以点B、D为圆心,AD、AB的长为半径画弧,两弧交于点C,连接CD、BC,则四边形ABCD是平行四边形,理由是 .
12.如图,在?ABCD中,E、F分别为AB、DC的中点,连接DE、EF、FB,则图中共有 个平行四边形.
13.如图,在Rt△ABC中,∠C=90°,AC=4,将△ABC沿CB向右平移得△DEF,若平移距离为2,则四边形ABED的面积等于 .
14. 如图,在四边形ABCD中,AB=CD,E、F在对角线AC上,且DE∥BF,AD∥BC,AE=CF,求证:四边形ABCD为平行四边形.
如图所示,已知在?ABCD中,AM=CN,求证:四边形MBND是平行四边形.
如图所示,已知AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,且AE=DF.求证四边形BECF是平行四边形.
17.如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.求证:
(1)AC=EF;
(2)四边形ADFE是平行四边形.
18.如图,△ABD、△ACE、△BCF分别是以△ABC的AB、AC、BC为边的等边三角形.求证:四边形ADFE是平行四边形.
答案:
1-10 CDADC BCBDB
11. 两组对边分别相等的四边形是平行四边形
12. 4
13. 8
14. 证明:∵DE∥BF,∴∠DEF=∠BFE,∴∠3=∠4.又AD∥BC,∴∠1=∠2.又AE=CF,∴△ADE≌△CBF,∴AD=BC,又AB=CD.∴四边形ABCD为平行四边形.
15. 证明:∵四边形ABCD是平行四边形,∴AB∥CD,且AB=CD,又AM=CN,∴BM綊DN,∴四边形MBND是平行四边形(一组对边平行且相等的四边形是平行四边形).
16. 证明:∵BE⊥AD,CF⊥AD,∴∠AEB=∠DFC=90°,∵AB∥CD,∴∠A=∠D,在△AEB和△DFC中,∠AEB=∠DFC,AE=DF,∠A=∠D,∴△AEB≌△DFC,∴BE=CF,∵BE⊥AD,CF⊥AD,∴BE∥CF,∴四边形BECF是平行四边形.
17. 证明:(1)在Rt△ABC中,∵∠BAC=30°,∴AB=2BC.∵△ABE是等边三角形,EF⊥AB,∴AB=2AF.∴AF=BC.在Rt△AFE和Rt△BCA中,∵,∴△AFE≌△BCA(HL),∴AC=EF;
(2)∵△ACD是等边三角形,∴∠DAC=60°,AC=AD,∴∠DAB=∠DAC+∠BAC=90°,∴AD⊥AB.又∵EF⊥AB,∴EF∥AD.∵AC=EF,AC=AD,∴EF=AD.∴四边形ADFE是平行四边形.
18. 证明:∵△ACE、△BCF都是等边三角形,∴CF=CB=BF,CA=CE=AE,∠ACE=∠FCB=60°,∴∠FCE=∠ACB,∴△FCE≌△BCA,∴EF=AB,∵AB=AD,∴AD=EF,同理可证AE=DF,∴四边形ADFE是平行四边形.
