2020-2021学年人教版八年级数学下册18.2特殊的平行四边形练习(Word版 有答案)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册18.2特殊的平行四边形练习(Word版 有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 21:48:47 | ||
图片预览




文档简介
特殊的平行四边形练习
一、选择题
1.
已知四边形ABCD中,对角线AC与BD相交于点O,AD//BC?,下列判断中错误的是(????)
A.
如果AB=CD,AC=BD,那么四边形ABCD是矩形?????????????
?B.
如果AB//CD,AC=BD,那么四边形ABCD是矩形?????????????
?C.
如果AD=BC,AC⊥BD,那么四边形ABCD是菱形?????????????
?D.
如果OA=OC,AC⊥BD,那么四边形ABCD是菱形?????????????
2.
下列命题中是真命题的是(??????)
A.
同位角相等?????????????
???????????????????????????
B.
对角线相等的四边形是平行四边形?????????????
?C.
四条边相等的四边形是菱形?????????????D.
矩形的对角线一定互相垂直?????????????
3.
如图,广场中心的菱形花坛ABCD的周长是40米,∠A=60°,则A,C两点之间的距离为(????)
?
A.
5米?????????????B.
米?????????????C.
10米?????????????D.
米?????????????
4.
如图,菱形ABCD的两条对角线相交于O,若AC=8,BD=6,则菱形ABCD的周长是( )
?
A.
32?????????????B.
24?????????????C.
40?????????????D.
20?????????????
5.
如果点E,F,G,H分别是菱形ABCD四边AB,BC,CD,DA上的中点,那么四边形EFGH是(
???).
A.
菱形?????????????B.
矩形?????????????C.
正方形?????????????D.
以上都不是?????????????
6.
矩形具有而一般平行四边形不具有的特殊性质是(
????)
A.
对边相等?????????????B.
对角线互相平分?????????????C.
对角线相等?????????????D.
对角相等?????????????
7.
如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为(????)
?
A.
?????????????B.
?????????????C.
?????????????D.
?????????????
8.如图,?的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=,AC=2,BD=4,则AE的长为 ( )
?
A.
?????????????B.
?????????????C.
?????????????D.
?????????????
9.
已知四边形ABCD和对角线AC,BD,顺次连接各边中点得四边形MNPQ,给出以下4个命题:①若所得四边形MNPQ为矩形,则ACBD;②若所得四边形MNPQ为菱形,则AC=?BD;③若所得四边形MNPQ为矩形,则;④若所得四边形MNPQ为菱形,则AB?=AD.
?以上命题中,正确的是(????)
A.
①②?????????????B.
③④?????????????C.
①③?????????????D.
①②③④?????????????
10.如图,在平面直角坐标系中,?的顶点A的坐标为(-4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,BD∶DC=3∶1,若函数y=(k>0,x>0)的图象经过点C,则k的值为 ( )
?
A.
?????????????B.
?????????????C.
?????????????D.
?????????????
二、填空题
11.
把20?cm长的铁丝剪成两段后,分别围成正方形,则两个正方形面积之和的最小值是________.
12.
如图,在△ABC中,AB?=AC,将△ABC绕点C旋转,得到△FEC,连接AE,BF,当__________时,四边形ABFE是矩形.
?
13.
如图,在正方形ABCD中,点E,F分别在边BC,CD上,△AEF是等边三角形,如果AB=1,那么CE的长是________.
?
三、解答题
14.如图,四边形ABCD中,AC,BD相交于点O?,O是AC的中点,AD∥BC,AC=8,BD=6.
?
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求的面积.
15.
如图,矩形ABCD中,AB=8,AD=6,点E,F分别在边CD,AB上.
?
(1)若DE=BF,求证:四边形AFCE是平行四边形;
(2)若四边形AFCE是菱形,求菱形AFCE的周长.
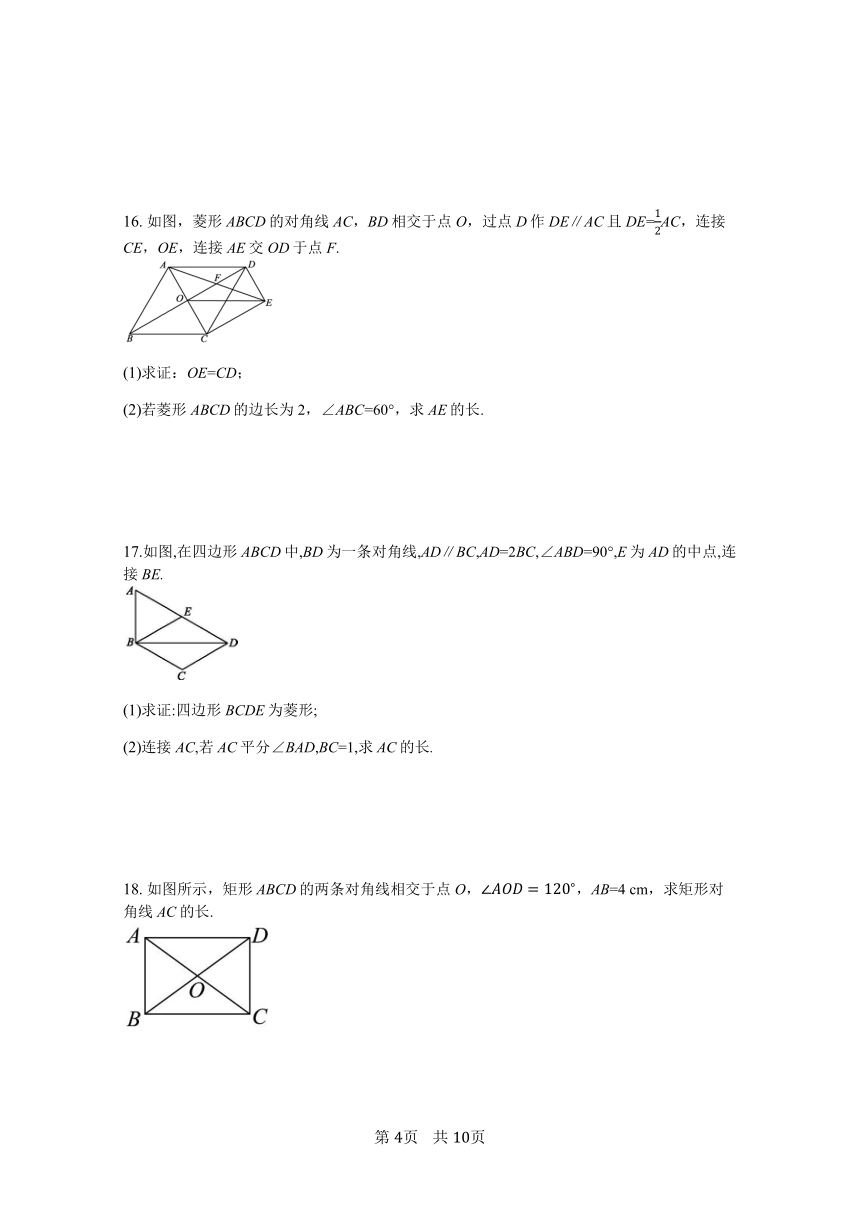
16.
如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DE∥AC且DE=AC,连接CE,OE,连接AE交OD于点F.
?
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
17.如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
?
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,BC=1,求AC的长.
18.
如图所示,矩形ABCD的两条对角线相交于点O,,AB=4?cm,求矩形对角线AC的长.
?
19.
如图,在矩形ABCD中,点E是BC上一点,且DE=DA,AF⊥DE于F,求证:AF=CD.
?
20.
如图,在△ABC中,AD是∠BAC的平分线,EF垂直平分AD交AB于E,交AC于F.求证:四边形AEDF是菱形.
?
21.
如图,在四边形ABCD中,BE=?DF,AC和EF互相平分于点O,.
?求证:四边形ABCD是矩形.
?
参考答案
1.
【答案】A【解析】A:由AD//BC,AB=CD不能判定四边形是平行四边形,组成的四边形可能是等腰梯形,故A错;B:由AD//BC,AB//CD得四边形ABCD是平行四边形,由AC=BD得对角线相等的平行四边形是矩形,B正确;C:由AD//BC,AB//CD得四边形ABCD是平行四边形,由AC⊥BD得对角线互相垂直的平行四边形是菱形,C正确;D:由AD//BC得∠ADO=∠CBO,又AC⊥BD,得∠AOD=∠COB,OA=OC,∴△AOD≌△COB,∴AD=BC,四边形ABCD是平行四边形,又AC⊥BD,得对角线互相垂直的平行四边形是菱形.故选A.
2.
【答案】C【解析】如图1,∠1与∠2是同位角,但不相等,故A错误;如图2,AC=BD,但四边形ABCD不是平行四边形,故B错误;四条边相等的四边形是菱形,正确,故C正确;如图4,矩形的对角线不一定垂直,故D错误.故选C.
?
3.
【答案】D【解析】设AC与BD交于点O.
?
?∵四边形ABCD为菱形,∴AC⊥BD,OA=OC,OB=OD,AB=BC=CD=AD=40÷4=10米,
?∵∠BAD=60°,∴△ABD为等边三角形,∴BD=AB=10米,OD=OB=5米,在Rt△AOB中,根据勾股定理得:OA=5米,∴AC=2OA=10米.故选D.
4.
【答案】D【解析】已知菱形ABCD的两条对角线相交于O,AC=8,BD=6,由菱形对角线互相垂直平分,可得BO=OD=3,AO=OC=4,在△AOB中,根据勾股定理可得AB=5,菱形的四条边都相等,周长为20,故选D.
5.
【答案】B【解析】如图,连接AC,BD,
?
?∵四边形ABCD为菱形,∴AC⊥BD.而点E,F,G,H分别是菱形ABCD四边的中点,
?∴EFAC,EF=AC,GH∥AC,GH=AC,∴EF∥GH,EF=GH,∴四边形EFGH为平行四边形,∵EF∥AC,FG∥BD,AC⊥BD,∴∠EFG=90°,∴四边形EFGH为矩形,
?故选B.
6.
【答案】C【解析】直接利用矩形的性质判断即可.
7.
【答案】A【解析】∵四边形ABCD是正方形,∴∠D=90°,∠ACD=45°,AD=CD=2,
?则S△ACD==,AC==,则EC=,
?∵△MEC是等腰直角三角形,∴S△MEC===,
?∴阴影部分的面积=S△ACD﹣S△MEC==.故选A.
8.
【答案】D【解析】∵四边形ABCD为平行四边形,∴OA=AC=1,OB=BD=2.在△AOB中,OA2+AB2=1+3=4=OB2,∴∠OAB=90°,∴BC=.?∵AE⊥BC,
?∠OAB=90°,∴AB·AC=BC·AE,∴AE=,故选D.
9.
【答案】A【解析】如图1,在矩形MNPQ中,M,N,P,Q分别是各边的中点,∴,PQ//AC//MN,PN//BD//QM,∴AC?BD,但,①正确,③不正确;如图2,∵四边形MNPQ为菱形,M,N,P,Q分别是各边的中点,∴MQ=PQ=PN?=MN,∴AC=BD,但,②正确,④不正确,故选A.
?
10.
【答案】D【解析】因为BD︰DC=3︰1,OA=4,所以点C的横坐标为1,因为∠DCO=∠BAO=60°,∠ODC=90°,DC=1,所以点C的纵坐标为,所以C(1,),因为函数y=的图象经过点C,所以k=xy=,故选D.
11.
【答案】cm2
?【解析】铁丝剪成两段后,分别围成正方形,∴两个正方形边长之和为5.设其中一个正方形的边长为xcm,则另一个正方形的边长为(5-x)cm,则两个正方形的面积和为,当x=面积有最小值.
12.
【答案】
?【解析】∵AC=CF,BC=CE,∴四边形ABFE是平行四边形,要使ABFE是矩形,只需AF=BE,即AC=BC,∴AC=BC=AB,因此△ABC是正三角形,∴,故应填60°.
13.
【答案】
?【解析】在正方形ABCD中,AB=AD,∠B=∠D=,△AEF是等边三角形,∴AE=AF,
?∴Rt△ABE≌Rt△ADF,∴BE=DF,∴CE=CF,设CE=CF=x,则BE=1-x,EF=AE=,在Rt△ABE中,由AB?+BE?=AE?得1?+(1-x)??=()?,解得x?=,x?=(舍去),∴CE长是.
14.
(1)
【答案】∵O是AC的中点,∴OA=OC,
?∵AD∥BC,∴∠ADO=∠CBO,
?在△AOD和△COB中,
?,
?∴△AOD≌△COB(AAS),
?∴OD=OB,
?∴四边形ABCD是平行四边形.
?(2)
【答案】∵四边形ABCD是平行四边形,AC⊥BD,
?∴四边形ABCD是菱形.
?∴S菱形ABCD=AC·BD=×8×6=24.
?
15.
(1)
【答案】∵四边形ABCD为矩形,∴AB=CD,AB∥CD,
?∵DE=BF,∴AF=CE,
?又∵AF∥CE,∴四边形AFCE是平行四边形.
?(2)
【答案】∵四边形AFCE是菱形,∴AE=CE,
?设DE=x,则AE=,CE=8-x,则,解得:x=,
?则菱形AFCE的边长为=,
?∴菱形AFCE周长为4×=25.
?
16.
(1)
【答案】在菱形ABCD中,OC=AC,AC⊥BD,∴DE=OC.
?∵DE∥AC,∴四边形OCED是矩形,∴OE=CD.
?(2)
【答案】在菱形ABCD中,∠ABC=60°,
?∴△ABC为等边三角形,AC=AB=2.
?∴在矩形OCED中,CE=?OD=.
?在Rt△ACE中,?AE=.
?
17.
(1)
【答案】∵AD=2BC,E为AD的中点,
?∴DE=BC.
?∵AD∥BC,
?∴四边形BCDE为平行四边形.
?∵∠ABD=90°,AE=DE,
?∴BE=DE,
?∴四边形BCDE为菱形.
?(2)
【答案】∵AD∥BC,AC平分∠BAD,
?∴∠BAC=∠DAC=∠BCA,
?∴AB=BC=1.
?∵AD=2BC=2,
?∴∠ADB=30°.
?∴∠DAC=30°,∠ADC=60°,
?∴∠ACD=90°.
?在Rt△ACD中,AD=2,CD=1,
?∴AC=.
?
?
18.
【答案】在四边形ABCD中,OA=OB,
?∵,∴,∴△AOB为等边三角形.∵AB?=4?cm,∴AC=2OA?=2AB=8?cm.
?
19.
【答案】证明:∵四边形ABCD是矩形,
?∴AD∥BC.
?∴∠ADE=∠DEC.
?∵AF⊥DE于F,
?∴∠AFD=∠C=90°.
?∵DE=DA,
?∴△ADF≌△DEC.
?∴AF=CD.
?
20.
【答案】证明:∵AD平分∠BAC,
?∴∠BAD=∠CAD,
?又∵EF⊥AD,
?∴∠AOE=∠AOF=90°
?在△AEO和△AFO中
?,
?∴△AEO≌△AFO(ASA),
?∴EO=FO.
?即EF,AD相互平分,
?∴四边形AEDF是平行四边形.
?又EF⊥AD,
?∴平行四边形AEDF为菱形.
21.
【答案】连接AF,CE.
?∵AC和EF互相平分,∴四边形AECF是平行四边形,∴AE?=CF,AE?//?CF.
?又∵BE=DF,∴AE+BE=CF+DF,即AB?=CD,∴四边形ABCD是平行四边形.
?又∵,∴四边形ABCD是矩形.
?
?
第10页
共10页
第9页
共10页
一、选择题
1.
已知四边形ABCD中,对角线AC与BD相交于点O,AD//BC?,下列判断中错误的是(????)
A.
如果AB=CD,AC=BD,那么四边形ABCD是矩形?????????????
?B.
如果AB//CD,AC=BD,那么四边形ABCD是矩形?????????????
?C.
如果AD=BC,AC⊥BD,那么四边形ABCD是菱形?????????????
?D.
如果OA=OC,AC⊥BD,那么四边形ABCD是菱形?????????????
2.
下列命题中是真命题的是(??????)
A.
同位角相等?????????????
???????????????????????????
B.
对角线相等的四边形是平行四边形?????????????
?C.
四条边相等的四边形是菱形?????????????D.
矩形的对角线一定互相垂直?????????????
3.
如图,广场中心的菱形花坛ABCD的周长是40米,∠A=60°,则A,C两点之间的距离为(????)
?
A.
5米?????????????B.
米?????????????C.
10米?????????????D.
米?????????????
4.
如图,菱形ABCD的两条对角线相交于O,若AC=8,BD=6,则菱形ABCD的周长是( )
?
A.
32?????????????B.
24?????????????C.
40?????????????D.
20?????????????
5.
如果点E,F,G,H分别是菱形ABCD四边AB,BC,CD,DA上的中点,那么四边形EFGH是(
???).
A.
菱形?????????????B.
矩形?????????????C.
正方形?????????????D.
以上都不是?????????????
6.
矩形具有而一般平行四边形不具有的特殊性质是(
????)
A.
对边相等?????????????B.
对角线互相平分?????????????C.
对角线相等?????????????D.
对角相等?????????????
7.
如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为(????)
?
A.
?????????????B.
?????????????C.
?????????????D.
?????????????
8.如图,?的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=,AC=2,BD=4,则AE的长为 ( )
?
A.
?????????????B.
?????????????C.
?????????????D.
?????????????
9.
已知四边形ABCD和对角线AC,BD,顺次连接各边中点得四边形MNPQ,给出以下4个命题:①若所得四边形MNPQ为矩形,则ACBD;②若所得四边形MNPQ为菱形,则AC=?BD;③若所得四边形MNPQ为矩形,则;④若所得四边形MNPQ为菱形,则AB?=AD.
?以上命题中,正确的是(????)
A.
①②?????????????B.
③④?????????????C.
①③?????????????D.
①②③④?????????????
10.如图,在平面直角坐标系中,?的顶点A的坐标为(-4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,BD∶DC=3∶1,若函数y=(k>0,x>0)的图象经过点C,则k的值为 ( )
?
A.
?????????????B.
?????????????C.
?????????????D.
?????????????
二、填空题
11.
把20?cm长的铁丝剪成两段后,分别围成正方形,则两个正方形面积之和的最小值是________.
12.
如图,在△ABC中,AB?=AC,将△ABC绕点C旋转,得到△FEC,连接AE,BF,当__________时,四边形ABFE是矩形.
?
13.
如图,在正方形ABCD中,点E,F分别在边BC,CD上,△AEF是等边三角形,如果AB=1,那么CE的长是________.
?
三、解答题
14.如图,四边形ABCD中,AC,BD相交于点O?,O是AC的中点,AD∥BC,AC=8,BD=6.
?
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求的面积.
15.
如图,矩形ABCD中,AB=8,AD=6,点E,F分别在边CD,AB上.
?
(1)若DE=BF,求证:四边形AFCE是平行四边形;
(2)若四边形AFCE是菱形,求菱形AFCE的周长.
16.
如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DE∥AC且DE=AC,连接CE,OE,连接AE交OD于点F.
?
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
17.如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
?
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,BC=1,求AC的长.
18.
如图所示,矩形ABCD的两条对角线相交于点O,,AB=4?cm,求矩形对角线AC的长.
?
19.
如图,在矩形ABCD中,点E是BC上一点,且DE=DA,AF⊥DE于F,求证:AF=CD.
?
20.
如图,在△ABC中,AD是∠BAC的平分线,EF垂直平分AD交AB于E,交AC于F.求证:四边形AEDF是菱形.
?
21.
如图,在四边形ABCD中,BE=?DF,AC和EF互相平分于点O,.
?求证:四边形ABCD是矩形.
?
参考答案
1.
【答案】A【解析】A:由AD//BC,AB=CD不能判定四边形是平行四边形,组成的四边形可能是等腰梯形,故A错;B:由AD//BC,AB//CD得四边形ABCD是平行四边形,由AC=BD得对角线相等的平行四边形是矩形,B正确;C:由AD//BC,AB//CD得四边形ABCD是平行四边形,由AC⊥BD得对角线互相垂直的平行四边形是菱形,C正确;D:由AD//BC得∠ADO=∠CBO,又AC⊥BD,得∠AOD=∠COB,OA=OC,∴△AOD≌△COB,∴AD=BC,四边形ABCD是平行四边形,又AC⊥BD,得对角线互相垂直的平行四边形是菱形.故选A.
2.
【答案】C【解析】如图1,∠1与∠2是同位角,但不相等,故A错误;如图2,AC=BD,但四边形ABCD不是平行四边形,故B错误;四条边相等的四边形是菱形,正确,故C正确;如图4,矩形的对角线不一定垂直,故D错误.故选C.
?
3.
【答案】D【解析】设AC与BD交于点O.
?
?∵四边形ABCD为菱形,∴AC⊥BD,OA=OC,OB=OD,AB=BC=CD=AD=40÷4=10米,
?∵∠BAD=60°,∴△ABD为等边三角形,∴BD=AB=10米,OD=OB=5米,在Rt△AOB中,根据勾股定理得:OA=5米,∴AC=2OA=10米.故选D.
4.
【答案】D【解析】已知菱形ABCD的两条对角线相交于O,AC=8,BD=6,由菱形对角线互相垂直平分,可得BO=OD=3,AO=OC=4,在△AOB中,根据勾股定理可得AB=5,菱形的四条边都相等,周长为20,故选D.
5.
【答案】B【解析】如图,连接AC,BD,
?
?∵四边形ABCD为菱形,∴AC⊥BD.而点E,F,G,H分别是菱形ABCD四边的中点,
?∴EFAC,EF=AC,GH∥AC,GH=AC,∴EF∥GH,EF=GH,∴四边形EFGH为平行四边形,∵EF∥AC,FG∥BD,AC⊥BD,∴∠EFG=90°,∴四边形EFGH为矩形,
?故选B.
6.
【答案】C【解析】直接利用矩形的性质判断即可.
7.
【答案】A【解析】∵四边形ABCD是正方形,∴∠D=90°,∠ACD=45°,AD=CD=2,
?则S△ACD==,AC==,则EC=,
?∵△MEC是等腰直角三角形,∴S△MEC===,
?∴阴影部分的面积=S△ACD﹣S△MEC==.故选A.
8.
【答案】D【解析】∵四边形ABCD为平行四边形,∴OA=AC=1,OB=BD=2.在△AOB中,OA2+AB2=1+3=4=OB2,∴∠OAB=90°,∴BC=.?∵AE⊥BC,
?∠OAB=90°,∴AB·AC=BC·AE,∴AE=,故选D.
9.
【答案】A【解析】如图1,在矩形MNPQ中,M,N,P,Q分别是各边的中点,∴,PQ//AC//MN,PN//BD//QM,∴AC?BD,但,①正确,③不正确;如图2,∵四边形MNPQ为菱形,M,N,P,Q分别是各边的中点,∴MQ=PQ=PN?=MN,∴AC=BD,但,②正确,④不正确,故选A.
?
10.
【答案】D【解析】因为BD︰DC=3︰1,OA=4,所以点C的横坐标为1,因为∠DCO=∠BAO=60°,∠ODC=90°,DC=1,所以点C的纵坐标为,所以C(1,),因为函数y=的图象经过点C,所以k=xy=,故选D.
11.
【答案】cm2
?【解析】铁丝剪成两段后,分别围成正方形,∴两个正方形边长之和为5.设其中一个正方形的边长为xcm,则另一个正方形的边长为(5-x)cm,则两个正方形的面积和为,当x=面积有最小值.
12.
【答案】
?【解析】∵AC=CF,BC=CE,∴四边形ABFE是平行四边形,要使ABFE是矩形,只需AF=BE,即AC=BC,∴AC=BC=AB,因此△ABC是正三角形,∴,故应填60°.
13.
【答案】
?【解析】在正方形ABCD中,AB=AD,∠B=∠D=,△AEF是等边三角形,∴AE=AF,
?∴Rt△ABE≌Rt△ADF,∴BE=DF,∴CE=CF,设CE=CF=x,则BE=1-x,EF=AE=,在Rt△ABE中,由AB?+BE?=AE?得1?+(1-x)??=()?,解得x?=,x?=(舍去),∴CE长是.
14.
(1)
【答案】∵O是AC的中点,∴OA=OC,
?∵AD∥BC,∴∠ADO=∠CBO,
?在△AOD和△COB中,
?,
?∴△AOD≌△COB(AAS),
?∴OD=OB,
?∴四边形ABCD是平行四边形.
?(2)
【答案】∵四边形ABCD是平行四边形,AC⊥BD,
?∴四边形ABCD是菱形.
?∴S菱形ABCD=AC·BD=×8×6=24.
?
15.
(1)
【答案】∵四边形ABCD为矩形,∴AB=CD,AB∥CD,
?∵DE=BF,∴AF=CE,
?又∵AF∥CE,∴四边形AFCE是平行四边形.
?(2)
【答案】∵四边形AFCE是菱形,∴AE=CE,
?设DE=x,则AE=,CE=8-x,则,解得:x=,
?则菱形AFCE的边长为=,
?∴菱形AFCE周长为4×=25.
?
16.
(1)
【答案】在菱形ABCD中,OC=AC,AC⊥BD,∴DE=OC.
?∵DE∥AC,∴四边形OCED是矩形,∴OE=CD.
?(2)
【答案】在菱形ABCD中,∠ABC=60°,
?∴△ABC为等边三角形,AC=AB=2.
?∴在矩形OCED中,CE=?OD=.
?在Rt△ACE中,?AE=.
?
17.
(1)
【答案】∵AD=2BC,E为AD的中点,
?∴DE=BC.
?∵AD∥BC,
?∴四边形BCDE为平行四边形.
?∵∠ABD=90°,AE=DE,
?∴BE=DE,
?∴四边形BCDE为菱形.
?(2)
【答案】∵AD∥BC,AC平分∠BAD,
?∴∠BAC=∠DAC=∠BCA,
?∴AB=BC=1.
?∵AD=2BC=2,
?∴∠ADB=30°.
?∴∠DAC=30°,∠ADC=60°,
?∴∠ACD=90°.
?在Rt△ACD中,AD=2,CD=1,
?∴AC=.
?
?
18.
【答案】在四边形ABCD中,OA=OB,
?∵,∴,∴△AOB为等边三角形.∵AB?=4?cm,∴AC=2OA?=2AB=8?cm.
?
19.
【答案】证明:∵四边形ABCD是矩形,
?∴AD∥BC.
?∴∠ADE=∠DEC.
?∵AF⊥DE于F,
?∴∠AFD=∠C=90°.
?∵DE=DA,
?∴△ADF≌△DEC.
?∴AF=CD.
?
20.
【答案】证明:∵AD平分∠BAC,
?∴∠BAD=∠CAD,
?又∵EF⊥AD,
?∴∠AOE=∠AOF=90°
?在△AEO和△AFO中
?,
?∴△AEO≌△AFO(ASA),
?∴EO=FO.
?即EF,AD相互平分,
?∴四边形AEDF是平行四边形.
?又EF⊥AD,
?∴平行四边形AEDF为菱形.
21.
【答案】连接AF,CE.
?∵AC和EF互相平分,∴四边形AECF是平行四边形,∴AE?=CF,AE?//?CF.
?又∵BE=DF,∴AE+BE=CF+DF,即AB?=CD,∴四边形ABCD是平行四边形.
?又∵,∴四边形ABCD是矩形.
?
?
第10页
共10页
第9页
共10页
