2020-2021学年辽宁省营口一中沿海分校九年级(下)期初数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年辽宁省营口一中沿海分校九年级(下)期初数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 947.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 07:38:00 | ||
图片预览




文档简介
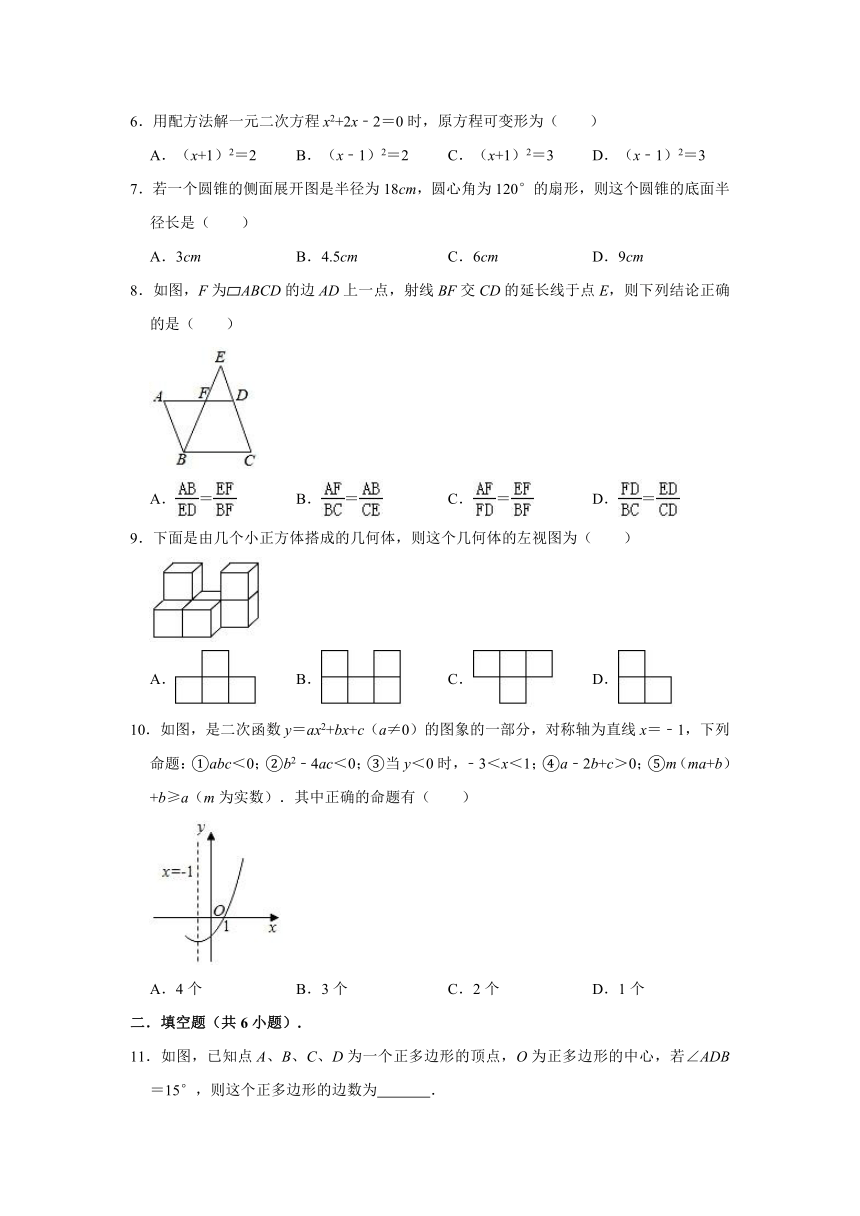
2020-2021学年辽宁省营口一中沿海分校九年级(下)期初数学试卷
一.选择题(共10小题).
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.若关于x的一元二次方程kx2﹣3x+2=0有实数根,则字母k的取值范围是( )
A.k<且k≠0 B.k≤ C.k< D.k≤且k≠0
3.下列事件中,是随机事件的是( )
A.画一个三角形,其内角和是180°
B.投掷一枚正六面体骰子,朝上一面的点数为5
C.在只装了红色卡片的袋子里,摸出一张白色卡片
D.明天太阳从东方升起
4.如图,AB是⊙O的直径,点D在⊙O上,若∠AOC=120°,则∠D的度数是( )
A.20° B.30° C.40° D.45°
5.函数与y=﹣mx2+m(m≠0)在同一直角坐标系中的大致图象可能是( )
A. B.
C. D.
6.用配方法解一元二次方程x2+2x﹣2=0时,原方程可变形为( )
A.(x+1)2=2 B.(x﹣1)2=2 C.(x+1)2=3 D.(x﹣1)2=3
7.若一个圆锥的侧面展开图是半径为18cm,圆心角为120°的扇形,则这个圆锥的底面半径长是( )
A.3cm B.4.5cm C.6cm D.9cm
8.如图,F为?ABCD的边AD上一点,射线BF交CD的延长线于点E,则下列结论正确的是( )
A.= B.= C.= D.=
9.下面是由几个小正方体搭成的几何体,则这个几何体的左视图为( )
A. B. C. D.
10.如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,对称轴为直线x=﹣1,下列命题:①abc<0;②b2﹣4ac<0;③当y<0时,﹣3<x<1;④a﹣2b+c>0;⑤m(ma+b)+b≥a(m为实数).其中正确的命题有( )
A.4个 B.3个 C.2个 D.1个
二.填空题(共6小题).
11.如图,已知点A、B、C、D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=15°,则这个正多边形的边数为 .
12.将抛物线y=x2向右平移2个单位长度,再向上平移1个单位长度,所得抛物线的函数表达式是 .
13.某批篮球的质量检验结果如下:
抽取的篮球数n 100 200 400 600 800 1000 1200
优等品的频数m 93 192 380 561 752 941 1128
优等品的频率 0.930 0.960 0.950 0.935 0.940 0.941 0.940
从这批篮球中,任意抽取一只篮球是优等品的概率的估计值是 .(精确到0.01)
14.如图,有一个池塘,要测量池塘两端A、B的距离,可先在平地上取一点O,从点O不经过池塘可以直接到达点A和点B,连接AO并延长到点C,连接BO并延长到点D,使==3,测得CD=36m,则池塘两端AB的距离为 m.
15.某种植物的一个主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干、小分支的总数为133,则每个支干长出多少个小分支?设每个支干长出x个小分支,依题意列方程,化成一般式为 .
16.如图,将含有30°角的直角三角板OAB放置在平面直角坐标系中,OB在x轴上,且A点坐标为(,1),若将三角板绕原点O顺时针旋转75°,则点A的对应点A1的坐标为 .
三.解答题(共9小题,满分102分)
17.解方程:
(1)9t2﹣(t﹣1)2=0.
(2)x2﹣5x﹣6=0.
18.如图,某居民小区改造,计划在居民小区的一块长50米,宽20米的矩形空地内修建两块相同的矩形绿地,使得两块矩形绿地之间及周边留有宽度相等的人行通道,且两块矩形绿地的面积之和为原矩形空地面积的,求人行通道的宽度是多少米?
19.为深化疫情防控国际合作、共同应对全球公共卫生危机,我国有序开展医疗物资出口工作.2020年10月,国内某企业口罩出口订单额为1000万元,2020年12月该企业口罩出口订单额为1210万元.
(1)求该企业2020年10月到12月口罩出口订单额的月平均增长率;
(2)按照(1)的月平均增长率,预计该企业2021年1月口罩出口订单额为多少万元?
20.某中学为了解九年级学生对新冠肺炎防控知识的掌握情况,从全校九年级学生中随机抽取部分学生进行调查.调查结果分为四类:A类﹣﹣非常了解;B类﹣﹣比较了解;C﹣﹣般了解;D类﹣﹣不了解.现将调查结果绘制成如图不完整的统计图,请根据统计图中的信息解答下列问题:
(1)本次共调查了 名学生.
(2)补全条形统计图.
(3)D类所对应扇形的圆心角的大小为 .
(4)已知D类中有2名女生,现从D类中随机抽取2名同学,试求恰好抽到一男一女的概率.
21.如图,一次函数y=﹣x+1的图象与两坐标轴分别交于A,B两点,与反比例函数的图象交于点C(﹣2,m).
(1)求反比例函数的解析式;
(2)若点P在y轴正半轴上,且与点B,C构成以BC为腰的等腰三角形,请直接写出所有符合条件的P点坐标.
22.“武汉加油!中国加油!”疫情牵动万人心,每个人都在为抗击疫情而努力.某厂改造了10条口罩生产线,每条生产线每天可生产口罩500个.如果每增加一条生产线,每条生产线就会比原来少生产20个口罩.设增加x条生产线后,每条生产线每天可生产口罩y个.
(1)直接写出y与x之间的函数关系式;
(2)设该厂每天可以生产的口罩w个,请求出w与x的函数关系式,并求出增加多少条生产线时,每天生产的口罩数量最多,最多为多少个?
23.如图,在Rt△ABC中,∠B=90°,AD平分∠BAC交BC于点D,点E在AC上,以AE为直径的⊙O经过点 D.
(1)求证:BC是⊙O的切线;
(2)若∠C=30°,且CD=3,试求阴影部分的面积.
24.△ABC与△CDE都是等边三角形,连接AD、BE.
(1)如图①,当点B、C、D在同一条直线上时,则∠BCE= 度;
(2)将图①中的△CDE绕着点C逆时针旋转到如图②的位置.求证:AD=BE.
25.如图直角坐标系中,O为坐标原点,抛物线y=﹣x2+6x+3交y轴于点A,过A作AB∥x轴,交抛物线于点B,连接OB.点P为抛物线上AB上方的一个点,连接PA,作PQ⊥AB垂足为H,交OB于点Q.
(1)求AB的长;
(2)当∠APQ=∠B时,求点P的坐标;
(3)当△APH面积是四边形AOQH面积的2倍时,求点P的坐标.
参考答案
一.选择题(共10小题).
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
解:A、是轴对称图形,也是中心对称图形,故此选项正确;
B、不是轴对称图形,也不是中心对称图形,故此选项错误;
C、是轴对称图形,不是中心对称图形,故此选项错误;
D、不是轴对称图形,是中心对称图形,故此选项错误;
故选:A.
2.若关于x的一元二次方程kx2﹣3x+2=0有实数根,则字母k的取值范围是( )
A.k<且k≠0 B.k≤ C.k< D.k≤且k≠0
解:根据题意得k≠0且△=(﹣3)2﹣4k×2≥0,
解得k≤且k≠0.
故选:D.
3.下列事件中,是随机事件的是( )
A.画一个三角形,其内角和是180°
B.投掷一枚正六面体骰子,朝上一面的点数为5
C.在只装了红色卡片的袋子里,摸出一张白色卡片
D.明天太阳从东方升起
解:A、画一个三角形,其内角和是180°,是必然事件;
B、投掷一枚正六面体骰子,朝上一面的点数为5,是随机事件;
C、在只装了红色卡片的袋子里,摸出一张白色卡片,是不可能事件;
D、明天太阳从东方升起,是必然事件;
故选:B.
4.如图,AB是⊙O的直径,点D在⊙O上,若∠AOC=120°,则∠D的度数是( )
A.20° B.30° C.40° D.45°
解:∵∠AOC=120°,
∴∠BOC=180°﹣∠AOC=60°,
∴∠BDC=∠BOC=30°.
故选:B.
5.函数与y=﹣mx2+m(m≠0)在同一直角坐标系中的大致图象可能是( )
A. B.
C. D.
解:由解析式y=﹣mx2+m可得:抛物线对称轴x=0;
A、由双曲线的两支分别位于二、四象限,可得m<0,则﹣m>0,抛物线开口方向向上、抛物线与y轴的交点为y轴的负半轴上;本图象与m的取值相矛盾,故A不符合题意;
B、由双曲线的两支分别位于一、三象限,可得m>0,则﹣m<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,本图象符合题意,故B符合题意;
C、由双曲线的两支分别位于一、三象限,可得m>0,则﹣m<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,本图象与m的取值相矛盾,故C不符合题意;
D、由双曲线的两支分别位于一、三象限,可得m>0,则﹣m<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,本图象与m的取值相矛盾,故D不符合题意.
故选:B.
6.用配方法解一元二次方程x2+2x﹣2=0时,原方程可变形为( )
A.(x+1)2=2 B.(x﹣1)2=2 C.(x+1)2=3 D.(x﹣1)2=3
解:∵x2+2x=2,
∴x2+2x+1=2+1,即(x+1)2=3,
故选:C.
7.若一个圆锥的侧面展开图是半径为18cm,圆心角为120°的扇形,则这个圆锥的底面半径长是( )
A.3cm B.4.5cm C.6cm D.9cm
解:设这个圆锥的底面半径为rcm,根据题意得2πr=,解得r=6,
所以这个圆锥的底面半径长为6cm.
故选:C.
8.如图,F为?ABCD的边AD上一点,射线BF交CD的延长线于点E,则下列结论正确的是( )
A.= B.= C.= D.=
解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴△ABF∽△DEF,△EFD∽△EBC,
∴,,,故选项A、C、D错误;
∵△ABF∽△DEF,△EFD∽△EBC,
∴△ABF∽△CEB,
∴,故选项B正确;
故选:B.
9.下面是由几个小正方体搭成的几何体,则这个几何体的左视图为( )
A. B. C. D.
解:左视图有2列,从左到右每列小正方形数目分别为2,1.
故选:D.
10.如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,对称轴为直线x=﹣1,下列命题:①abc<0;②b2﹣4ac<0;③当y<0时,﹣3<x<1;④a﹣2b+c>0;⑤m(ma+b)+b≥a(m为实数).其中正确的命题有( )
A.4个 B.3个 C.2个 D.1个
解:①∵抛物线开口向上,
∴a>0,
∵对称轴为直线x=﹣1,
∴b>0,
抛物线与y轴交于负半轴,
∴c<0,
∴abc<0,本小题说法正确;
②∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,本小题说法错误;
③∵抛物线与x轴的交点为(1,0),对称轴为直线x=﹣1,
∴抛物线与x轴的另一个交点为(﹣3,0),
∴当y<0时,﹣3<x<1,本小题说法正确;
④∵对称轴为直线x=﹣1,
∴﹣=﹣1,
∴b=2a,
∵抛物线与x轴的交点为(1,0),
∴a+b+c=0,
∴c=﹣3a,
∴a﹣2b+c=a﹣4a﹣3a=﹣6a<0,本小题说法错误;
⑤∵对称轴为直线x=﹣1,
∴当x=﹣1时,y有最小值,
∴am2+bm+c≥a﹣b+c,
∴m(ma+b)+b≥a(m为实数),本小题说法正确;
故选:B.
二.填空题(共6小题,满分18分,每小题3分)
11.如图,已知点A、B、C、D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=15°,则这个正多边形的边数为 12 .
解:连接OA,OB,
∵A、B、C、D为一个正多边形的顶点,O为正多边形的中心,
∴点A、B、C、D在以点O为圆心,OA为半径的同一个圆上,
∵∠ADB=15°,
∴∠AOB=2∠ADB=30°,
∴这个正多边形的边数==12,
故答案为:12.
12.将抛物线y=x2向右平移2个单位长度,再向上平移1个单位长度,所得抛物线的函数表达式是 y=(x﹣2)2+1 .
解:将抛物线y=x2向右平移2个单位长度,再向上平移1个单位长度,所得抛物线的函数表达式是y=(x﹣2)2+1,
故答案为:y=(x﹣2)2+1.
13.某批篮球的质量检验结果如下:
抽取的篮球数n 100 200 400 600 800 1000 1200
优等品的频数m 93 192 380 561 752 941 1128
优等品的频率 0.930 0.960 0.950 0.935 0.940 0.941 0.940
从这批篮球中,任意抽取一只篮球是优等品的概率的估计值是 0.94 .(精确到0.01)
解:从这批篮球中,任意抽取一只篮球是优等品的概率的估计值是0.94.
故答案为0.94.
14.如图,有一个池塘,要测量池塘两端A、B的距离,可先在平地上取一点O,从点O不经过池塘可以直接到达点A和点B,连接AO并延长到点C,连接BO并延长到点D,使==3,测得CD=36m,则池塘两端AB的距离为 108 m.
解:∵==3,∠AOB=∠COD,
∴△AOB∽△COD,
∴===3,
∵CD=36m,
∴AB=3CD=108米.
故答案为:108.
15.某种植物的一个主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干、小分支的总数为133,则每个支干长出多少个小分支?设每个支干长出x个小分支,依题意列方程,化成一般式为 x2+x﹣132=0 .
解:依题意得:1+x+x2=133,
整理得:x2+x﹣132=0.
故答案为:x2+x﹣132=0.
16.如图,将含有30°角的直角三角板OAB放置在平面直角坐标系中,OB在x轴上,且A点坐标为(,1),若将三角板绕原点O顺时针旋转75°,则点A的对应点A1的坐标为 (,﹣) .
解:如图所示:过点A1作A1C⊥OB.
∵将三角板绕原点O顺时针旋转75°,
∴∠AOA1=75°,OA1=OA.
∴∠COA1=45°.
∵A(,1),
∴OA==2,
∴OC=2×=,CA1=2×=.
∴A1的坐标为(,﹣).
故答案为(,﹣).
三.解答题(共9小题,满分102分)
17.解方程:
(1)9t2﹣(t﹣1)2=0.
(2)x2﹣5x﹣6=0.
解:(1)∵9t2﹣(t﹣1)2=0,
∴(3t﹣t+1)(3t+t﹣1)=0,即(2t+1)(4t﹣1)=0,
∴2t+1=0或4t﹣1=0,
解得t1=﹣,t2=.
(2)∵x2﹣5x﹣6=0,
∴(x﹣6)(x+1)=0,
∴x﹣6=0或x+1=0,
解得x1=6,x2=﹣1.
18.如图,某居民小区改造,计划在居民小区的一块长50米,宽20米的矩形空地内修建两块相同的矩形绿地,使得两块矩形绿地之间及周边留有宽度相等的人行通道,且两块矩形绿地的面积之和为原矩形空地面积的,求人行通道的宽度是多少米?
解:设人行通道的宽度是x米,则两块绿地可合成长为(50﹣3x)米、宽为(20﹣2x)米的矩形,
根据题意得:(50﹣3x)(20﹣2x)=×50×20,
整理得:x1=25(舍去),x2=,
∴x=.
答:人行通道的宽度是米.
19.为深化疫情防控国际合作、共同应对全球公共卫生危机,我国有序开展医疗物资出口工作.2020年10月,国内某企业口罩出口订单额为1000万元,2020年12月该企业口罩出口订单额为1210万元.
(1)求该企业2020年10月到12月口罩出口订单额的月平均增长率;
(2)按照(1)的月平均增长率,预计该企业2021年1月口罩出口订单额为多少万元?
解:(1)设该企业2020年10月到12月口罩出口订单额的月平均增长率为x,
依题意得:1000(1+x)2=1210,
解得:x1=0.1=10%,x2=﹣2.1(不合题意,舍去).
答:该企业2020年10月到12月口罩出口订单额的月平均增长率为10%.
(2)1210×(1+10%)=1331(万元).
答:预计该企业2021年1月口罩出口订单额为1331万元.
20.某中学为了解九年级学生对新冠肺炎防控知识的掌握情况,从全校九年级学生中随机抽取部分学生进行调查.调查结果分为四类:A类﹣﹣非常了解;B类﹣﹣比较了解;C﹣﹣般了解;D类﹣﹣不了解.现将调查结果绘制成如图不完整的统计图,请根据统计图中的信息解答下列问题:
(1)本次共调查了 50 名学生.
(2)补全条形统计图.
(3)D类所对应扇形的圆心角的大小为 36° .
(4)已知D类中有2名女生,现从D类中随机抽取2名同学,试求恰好抽到一男一女的概率.
解:(1)本次共调查的学生数为:20÷40%=50(名),
故答案为:50;
(2)C类学生人数为:50﹣15﹣20﹣5=10(名),
补全条形统计图如下:
(3)D类所对应扇形的圆心角为:360°×=36°,
故答案为:36°;
(4)画树状图如图:
共有20个等可能的结果,恰好抽到一男一女的结果有12个,
∴恰好抽到一男一女的概率为=.
21.如图,一次函数y=﹣x+1的图象与两坐标轴分别交于A,B两点,与反比例函数的图象交于点C(﹣2,m).
(1)求反比例函数的解析式;
(2)若点P在y轴正半轴上,且与点B,C构成以BC为腰的等腰三角形,请直接写出所有符合条件的P点坐标.
解:(1)∵点C(﹣2,m)在一次函数y=﹣x+1的图象上,
把C点坐标代入y=﹣x+1,得m=﹣(﹣2)+1=3,
∴点C的坐标是(﹣2,3),
设反比例函数的解析式为,
把点C的坐标(﹣2,3)代入得,,
解得k=﹣6,
∴反比例函数的解析式为;
(2)在直线y=﹣x+1中,令x=0,则y=1,
∴B(0,1),
由(1)知,C(﹣2,3),
∴BC==2,
当BC=BP时,BP=2,
∴OP=2+1,
∴P(0,2+1),
当BC=PC时,点C在BP的垂直平分线,
∴P(0,5),
即满足条件的点P的坐标为(0,5)或(0,).
22.“武汉加油!中国加油!”疫情牵动万人心,每个人都在为抗击疫情而努力.某厂改造了10条口罩生产线,每条生产线每天可生产口罩500个.如果每增加一条生产线,每条生产线就会比原来少生产20个口罩.设增加x条生产线后,每条生产线每天可生产口罩y个.
(1)直接写出y与x之间的函数关系式;
(2)设该厂每天可以生产的口罩w个,请求出w与x的函数关系式,并求出增加多少条生产线时,每天生产的口罩数量最多,最多为多少个?
解:(1)由题意可知该函数关系为一次函数,其解析式为:y=500﹣20x;
∴y与x之间的函数关系式为y=500﹣20x(0≤x≤25,且x为整数);
(2)w=(10+x)(500﹣20x)
=﹣20x2+300x+5000
=﹣20(x﹣7.5)2+6125,
∵a=﹣20<0,开口向下,
∴当x=7.5时,w最大,
又∵x为整数,
∴当x=7或8时,w最大,最大值为6120.
答:当增加7或8条生产线时,每天生产的口罩数量最多,为6120个.
23.如图,在Rt△ABC中,∠B=90°,AD平分∠BAC交BC于点D,点E在AC上,以AE为直径的⊙O经过点 D.
(1)求证:BC是⊙O的切线;
(2)若∠C=30°,且CD=3,试求阴影部分的面积.
解:(1)连接OD,
∵AD是∠BAC的平分线,
∴∠DAB=∠DAO,
∵OD=OA,
∴∠DAO=∠ODA,
则∠DAB=∠ODA,
∴DO∥AB,而∠B=90°,
∴∠ODB=90°,
∴BC是⊙O的切线;
(2)连接DE、OD、DF、OF,设圆的半径为R,
∵∠C=30°,CD=3,
∴OD=CD?tan30°=3×=3,
∵∠DAB=∠DAE=30°,
∴=,
∵∠DOE=60°,
∴∠DOF=60°,
∴∠FOA=60°,
∴△OFD、△OFA是等边三角形,
∴DF∥AC,
∴S阴影=S扇形DFO==.
24.△ABC与△CDE都是等边三角形,连接AD、BE.
(1)如图①,当点B、C、D在同一条直线上时,则∠BCE= 120 度;
(2)将图①中的△CDE绕着点C逆时针旋转到如图②的位置.求证:AD=BE.
解:(1)∵△CDE是等边三角形,
∴∠DCE=60°,
∵点B、C、D在同一条直线,
∴∠BCE+∠DCE=180°,
∴∠BCE=180°﹣∠DCE=120°,
故答案为:120;
(2)∵△ABC与△CDE都是等边三角形,
∴BC=AC,CE=CD,∠ACB=∠DCE=60°,
∴∠ACB+∠ACE=∠DCE+∠ACE,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS),
∴BE=AD.
25.如图直角坐标系中,O为坐标原点,抛物线y=﹣x2+6x+3交y轴于点A,过A作AB∥x轴,交抛物线于点B,连接OB.点P为抛物线上AB上方的一个点,连接PA,作PQ⊥AB垂足为H,交OB于点Q.
(1)求AB的长;
(2)当∠APQ=∠B时,求点P的坐标;
(3)当△APH面积是四边形AOQH面积的2倍时,求点P的坐标.
解:(1)对于y=﹣x2+6x+3,令x=0,则y=3,故点A(0,3),
令y=﹣x2+6x+3=3,解得x=0或6,故点B(6,3),
故AB=6;
(2)设P(m,﹣m2+6m+3),
∵∠P=∠B,∠AHP=∠OAB=90°,
∴△ABO~△HPA,故,
∴=,
解得m=4.
∴P(4,11);
(3)当△APH的面积是四边形AOQH的面积的2倍时,
则2(AO+HQ)=PH,
∴2(3+)=﹣m2+6m,
解得:m1=4,m2=3,
∴P(4,11)或P(3,12).
一.选择题(共10小题).
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.若关于x的一元二次方程kx2﹣3x+2=0有实数根,则字母k的取值范围是( )
A.k<且k≠0 B.k≤ C.k< D.k≤且k≠0
3.下列事件中,是随机事件的是( )
A.画一个三角形,其内角和是180°
B.投掷一枚正六面体骰子,朝上一面的点数为5
C.在只装了红色卡片的袋子里,摸出一张白色卡片
D.明天太阳从东方升起
4.如图,AB是⊙O的直径,点D在⊙O上,若∠AOC=120°,则∠D的度数是( )
A.20° B.30° C.40° D.45°
5.函数与y=﹣mx2+m(m≠0)在同一直角坐标系中的大致图象可能是( )
A. B.
C. D.
6.用配方法解一元二次方程x2+2x﹣2=0时,原方程可变形为( )
A.(x+1)2=2 B.(x﹣1)2=2 C.(x+1)2=3 D.(x﹣1)2=3
7.若一个圆锥的侧面展开图是半径为18cm,圆心角为120°的扇形,则这个圆锥的底面半径长是( )
A.3cm B.4.5cm C.6cm D.9cm
8.如图,F为?ABCD的边AD上一点,射线BF交CD的延长线于点E,则下列结论正确的是( )
A.= B.= C.= D.=
9.下面是由几个小正方体搭成的几何体,则这个几何体的左视图为( )
A. B. C. D.
10.如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,对称轴为直线x=﹣1,下列命题:①abc<0;②b2﹣4ac<0;③当y<0时,﹣3<x<1;④a﹣2b+c>0;⑤m(ma+b)+b≥a(m为实数).其中正确的命题有( )
A.4个 B.3个 C.2个 D.1个
二.填空题(共6小题).
11.如图,已知点A、B、C、D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=15°,则这个正多边形的边数为 .
12.将抛物线y=x2向右平移2个单位长度,再向上平移1个单位长度,所得抛物线的函数表达式是 .
13.某批篮球的质量检验结果如下:
抽取的篮球数n 100 200 400 600 800 1000 1200
优等品的频数m 93 192 380 561 752 941 1128
优等品的频率 0.930 0.960 0.950 0.935 0.940 0.941 0.940
从这批篮球中,任意抽取一只篮球是优等品的概率的估计值是 .(精确到0.01)
14.如图,有一个池塘,要测量池塘两端A、B的距离,可先在平地上取一点O,从点O不经过池塘可以直接到达点A和点B,连接AO并延长到点C,连接BO并延长到点D,使==3,测得CD=36m,则池塘两端AB的距离为 m.
15.某种植物的一个主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干、小分支的总数为133,则每个支干长出多少个小分支?设每个支干长出x个小分支,依题意列方程,化成一般式为 .
16.如图,将含有30°角的直角三角板OAB放置在平面直角坐标系中,OB在x轴上,且A点坐标为(,1),若将三角板绕原点O顺时针旋转75°,则点A的对应点A1的坐标为 .
三.解答题(共9小题,满分102分)
17.解方程:
(1)9t2﹣(t﹣1)2=0.
(2)x2﹣5x﹣6=0.
18.如图,某居民小区改造,计划在居民小区的一块长50米,宽20米的矩形空地内修建两块相同的矩形绿地,使得两块矩形绿地之间及周边留有宽度相等的人行通道,且两块矩形绿地的面积之和为原矩形空地面积的,求人行通道的宽度是多少米?
19.为深化疫情防控国际合作、共同应对全球公共卫生危机,我国有序开展医疗物资出口工作.2020年10月,国内某企业口罩出口订单额为1000万元,2020年12月该企业口罩出口订单额为1210万元.
(1)求该企业2020年10月到12月口罩出口订单额的月平均增长率;
(2)按照(1)的月平均增长率,预计该企业2021年1月口罩出口订单额为多少万元?
20.某中学为了解九年级学生对新冠肺炎防控知识的掌握情况,从全校九年级学生中随机抽取部分学生进行调查.调查结果分为四类:A类﹣﹣非常了解;B类﹣﹣比较了解;C﹣﹣般了解;D类﹣﹣不了解.现将调查结果绘制成如图不完整的统计图,请根据统计图中的信息解答下列问题:
(1)本次共调查了 名学生.
(2)补全条形统计图.
(3)D类所对应扇形的圆心角的大小为 .
(4)已知D类中有2名女生,现从D类中随机抽取2名同学,试求恰好抽到一男一女的概率.
21.如图,一次函数y=﹣x+1的图象与两坐标轴分别交于A,B两点,与反比例函数的图象交于点C(﹣2,m).
(1)求反比例函数的解析式;
(2)若点P在y轴正半轴上,且与点B,C构成以BC为腰的等腰三角形,请直接写出所有符合条件的P点坐标.
22.“武汉加油!中国加油!”疫情牵动万人心,每个人都在为抗击疫情而努力.某厂改造了10条口罩生产线,每条生产线每天可生产口罩500个.如果每增加一条生产线,每条生产线就会比原来少生产20个口罩.设增加x条生产线后,每条生产线每天可生产口罩y个.
(1)直接写出y与x之间的函数关系式;
(2)设该厂每天可以生产的口罩w个,请求出w与x的函数关系式,并求出增加多少条生产线时,每天生产的口罩数量最多,最多为多少个?
23.如图,在Rt△ABC中,∠B=90°,AD平分∠BAC交BC于点D,点E在AC上,以AE为直径的⊙O经过点 D.
(1)求证:BC是⊙O的切线;
(2)若∠C=30°,且CD=3,试求阴影部分的面积.
24.△ABC与△CDE都是等边三角形,连接AD、BE.
(1)如图①,当点B、C、D在同一条直线上时,则∠BCE= 度;
(2)将图①中的△CDE绕着点C逆时针旋转到如图②的位置.求证:AD=BE.
25.如图直角坐标系中,O为坐标原点,抛物线y=﹣x2+6x+3交y轴于点A,过A作AB∥x轴,交抛物线于点B,连接OB.点P为抛物线上AB上方的一个点,连接PA,作PQ⊥AB垂足为H,交OB于点Q.
(1)求AB的长;
(2)当∠APQ=∠B时,求点P的坐标;
(3)当△APH面积是四边形AOQH面积的2倍时,求点P的坐标.
参考答案
一.选择题(共10小题).
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
解:A、是轴对称图形,也是中心对称图形,故此选项正确;
B、不是轴对称图形,也不是中心对称图形,故此选项错误;
C、是轴对称图形,不是中心对称图形,故此选项错误;
D、不是轴对称图形,是中心对称图形,故此选项错误;
故选:A.
2.若关于x的一元二次方程kx2﹣3x+2=0有实数根,则字母k的取值范围是( )
A.k<且k≠0 B.k≤ C.k< D.k≤且k≠0
解:根据题意得k≠0且△=(﹣3)2﹣4k×2≥0,
解得k≤且k≠0.
故选:D.
3.下列事件中,是随机事件的是( )
A.画一个三角形,其内角和是180°
B.投掷一枚正六面体骰子,朝上一面的点数为5
C.在只装了红色卡片的袋子里,摸出一张白色卡片
D.明天太阳从东方升起
解:A、画一个三角形,其内角和是180°,是必然事件;
B、投掷一枚正六面体骰子,朝上一面的点数为5,是随机事件;
C、在只装了红色卡片的袋子里,摸出一张白色卡片,是不可能事件;
D、明天太阳从东方升起,是必然事件;
故选:B.
4.如图,AB是⊙O的直径,点D在⊙O上,若∠AOC=120°,则∠D的度数是( )
A.20° B.30° C.40° D.45°
解:∵∠AOC=120°,
∴∠BOC=180°﹣∠AOC=60°,
∴∠BDC=∠BOC=30°.
故选:B.
5.函数与y=﹣mx2+m(m≠0)在同一直角坐标系中的大致图象可能是( )
A. B.
C. D.
解:由解析式y=﹣mx2+m可得:抛物线对称轴x=0;
A、由双曲线的两支分别位于二、四象限,可得m<0,则﹣m>0,抛物线开口方向向上、抛物线与y轴的交点为y轴的负半轴上;本图象与m的取值相矛盾,故A不符合题意;
B、由双曲线的两支分别位于一、三象限,可得m>0,则﹣m<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,本图象符合题意,故B符合题意;
C、由双曲线的两支分别位于一、三象限,可得m>0,则﹣m<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,本图象与m的取值相矛盾,故C不符合题意;
D、由双曲线的两支分别位于一、三象限,可得m>0,则﹣m<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,本图象与m的取值相矛盾,故D不符合题意.
故选:B.
6.用配方法解一元二次方程x2+2x﹣2=0时,原方程可变形为( )
A.(x+1)2=2 B.(x﹣1)2=2 C.(x+1)2=3 D.(x﹣1)2=3
解:∵x2+2x=2,
∴x2+2x+1=2+1,即(x+1)2=3,
故选:C.
7.若一个圆锥的侧面展开图是半径为18cm,圆心角为120°的扇形,则这个圆锥的底面半径长是( )
A.3cm B.4.5cm C.6cm D.9cm
解:设这个圆锥的底面半径为rcm,根据题意得2πr=,解得r=6,
所以这个圆锥的底面半径长为6cm.
故选:C.
8.如图,F为?ABCD的边AD上一点,射线BF交CD的延长线于点E,则下列结论正确的是( )
A.= B.= C.= D.=
解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴△ABF∽△DEF,△EFD∽△EBC,
∴,,,故选项A、C、D错误;
∵△ABF∽△DEF,△EFD∽△EBC,
∴△ABF∽△CEB,
∴,故选项B正确;
故选:B.
9.下面是由几个小正方体搭成的几何体,则这个几何体的左视图为( )
A. B. C. D.
解:左视图有2列,从左到右每列小正方形数目分别为2,1.
故选:D.
10.如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,对称轴为直线x=﹣1,下列命题:①abc<0;②b2﹣4ac<0;③当y<0时,﹣3<x<1;④a﹣2b+c>0;⑤m(ma+b)+b≥a(m为实数).其中正确的命题有( )
A.4个 B.3个 C.2个 D.1个
解:①∵抛物线开口向上,
∴a>0,
∵对称轴为直线x=﹣1,
∴b>0,
抛物线与y轴交于负半轴,
∴c<0,
∴abc<0,本小题说法正确;
②∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,本小题说法错误;
③∵抛物线与x轴的交点为(1,0),对称轴为直线x=﹣1,
∴抛物线与x轴的另一个交点为(﹣3,0),
∴当y<0时,﹣3<x<1,本小题说法正确;
④∵对称轴为直线x=﹣1,
∴﹣=﹣1,
∴b=2a,
∵抛物线与x轴的交点为(1,0),
∴a+b+c=0,
∴c=﹣3a,
∴a﹣2b+c=a﹣4a﹣3a=﹣6a<0,本小题说法错误;
⑤∵对称轴为直线x=﹣1,
∴当x=﹣1时,y有最小值,
∴am2+bm+c≥a﹣b+c,
∴m(ma+b)+b≥a(m为实数),本小题说法正确;
故选:B.
二.填空题(共6小题,满分18分,每小题3分)
11.如图,已知点A、B、C、D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=15°,则这个正多边形的边数为 12 .
解:连接OA,OB,
∵A、B、C、D为一个正多边形的顶点,O为正多边形的中心,
∴点A、B、C、D在以点O为圆心,OA为半径的同一个圆上,
∵∠ADB=15°,
∴∠AOB=2∠ADB=30°,
∴这个正多边形的边数==12,
故答案为:12.
12.将抛物线y=x2向右平移2个单位长度,再向上平移1个单位长度,所得抛物线的函数表达式是 y=(x﹣2)2+1 .
解:将抛物线y=x2向右平移2个单位长度,再向上平移1个单位长度,所得抛物线的函数表达式是y=(x﹣2)2+1,
故答案为:y=(x﹣2)2+1.
13.某批篮球的质量检验结果如下:
抽取的篮球数n 100 200 400 600 800 1000 1200
优等品的频数m 93 192 380 561 752 941 1128
优等品的频率 0.930 0.960 0.950 0.935 0.940 0.941 0.940
从这批篮球中,任意抽取一只篮球是优等品的概率的估计值是 0.94 .(精确到0.01)
解:从这批篮球中,任意抽取一只篮球是优等品的概率的估计值是0.94.
故答案为0.94.
14.如图,有一个池塘,要测量池塘两端A、B的距离,可先在平地上取一点O,从点O不经过池塘可以直接到达点A和点B,连接AO并延长到点C,连接BO并延长到点D,使==3,测得CD=36m,则池塘两端AB的距离为 108 m.
解:∵==3,∠AOB=∠COD,
∴△AOB∽△COD,
∴===3,
∵CD=36m,
∴AB=3CD=108米.
故答案为:108.
15.某种植物的一个主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干、小分支的总数为133,则每个支干长出多少个小分支?设每个支干长出x个小分支,依题意列方程,化成一般式为 x2+x﹣132=0 .
解:依题意得:1+x+x2=133,
整理得:x2+x﹣132=0.
故答案为:x2+x﹣132=0.
16.如图,将含有30°角的直角三角板OAB放置在平面直角坐标系中,OB在x轴上,且A点坐标为(,1),若将三角板绕原点O顺时针旋转75°,则点A的对应点A1的坐标为 (,﹣) .
解:如图所示:过点A1作A1C⊥OB.
∵将三角板绕原点O顺时针旋转75°,
∴∠AOA1=75°,OA1=OA.
∴∠COA1=45°.
∵A(,1),
∴OA==2,
∴OC=2×=,CA1=2×=.
∴A1的坐标为(,﹣).
故答案为(,﹣).
三.解答题(共9小题,满分102分)
17.解方程:
(1)9t2﹣(t﹣1)2=0.
(2)x2﹣5x﹣6=0.
解:(1)∵9t2﹣(t﹣1)2=0,
∴(3t﹣t+1)(3t+t﹣1)=0,即(2t+1)(4t﹣1)=0,
∴2t+1=0或4t﹣1=0,
解得t1=﹣,t2=.
(2)∵x2﹣5x﹣6=0,
∴(x﹣6)(x+1)=0,
∴x﹣6=0或x+1=0,
解得x1=6,x2=﹣1.
18.如图,某居民小区改造,计划在居民小区的一块长50米,宽20米的矩形空地内修建两块相同的矩形绿地,使得两块矩形绿地之间及周边留有宽度相等的人行通道,且两块矩形绿地的面积之和为原矩形空地面积的,求人行通道的宽度是多少米?
解:设人行通道的宽度是x米,则两块绿地可合成长为(50﹣3x)米、宽为(20﹣2x)米的矩形,
根据题意得:(50﹣3x)(20﹣2x)=×50×20,
整理得:x1=25(舍去),x2=,
∴x=.
答:人行通道的宽度是米.
19.为深化疫情防控国际合作、共同应对全球公共卫生危机,我国有序开展医疗物资出口工作.2020年10月,国内某企业口罩出口订单额为1000万元,2020年12月该企业口罩出口订单额为1210万元.
(1)求该企业2020年10月到12月口罩出口订单额的月平均增长率;
(2)按照(1)的月平均增长率,预计该企业2021年1月口罩出口订单额为多少万元?
解:(1)设该企业2020年10月到12月口罩出口订单额的月平均增长率为x,
依题意得:1000(1+x)2=1210,
解得:x1=0.1=10%,x2=﹣2.1(不合题意,舍去).
答:该企业2020年10月到12月口罩出口订单额的月平均增长率为10%.
(2)1210×(1+10%)=1331(万元).
答:预计该企业2021年1月口罩出口订单额为1331万元.
20.某中学为了解九年级学生对新冠肺炎防控知识的掌握情况,从全校九年级学生中随机抽取部分学生进行调查.调查结果分为四类:A类﹣﹣非常了解;B类﹣﹣比较了解;C﹣﹣般了解;D类﹣﹣不了解.现将调查结果绘制成如图不完整的统计图,请根据统计图中的信息解答下列问题:
(1)本次共调查了 50 名学生.
(2)补全条形统计图.
(3)D类所对应扇形的圆心角的大小为 36° .
(4)已知D类中有2名女生,现从D类中随机抽取2名同学,试求恰好抽到一男一女的概率.
解:(1)本次共调查的学生数为:20÷40%=50(名),
故答案为:50;
(2)C类学生人数为:50﹣15﹣20﹣5=10(名),
补全条形统计图如下:
(3)D类所对应扇形的圆心角为:360°×=36°,
故答案为:36°;
(4)画树状图如图:
共有20个等可能的结果,恰好抽到一男一女的结果有12个,
∴恰好抽到一男一女的概率为=.
21.如图,一次函数y=﹣x+1的图象与两坐标轴分别交于A,B两点,与反比例函数的图象交于点C(﹣2,m).
(1)求反比例函数的解析式;
(2)若点P在y轴正半轴上,且与点B,C构成以BC为腰的等腰三角形,请直接写出所有符合条件的P点坐标.
解:(1)∵点C(﹣2,m)在一次函数y=﹣x+1的图象上,
把C点坐标代入y=﹣x+1,得m=﹣(﹣2)+1=3,
∴点C的坐标是(﹣2,3),
设反比例函数的解析式为,
把点C的坐标(﹣2,3)代入得,,
解得k=﹣6,
∴反比例函数的解析式为;
(2)在直线y=﹣x+1中,令x=0,则y=1,
∴B(0,1),
由(1)知,C(﹣2,3),
∴BC==2,
当BC=BP时,BP=2,
∴OP=2+1,
∴P(0,2+1),
当BC=PC时,点C在BP的垂直平分线,
∴P(0,5),
即满足条件的点P的坐标为(0,5)或(0,).
22.“武汉加油!中国加油!”疫情牵动万人心,每个人都在为抗击疫情而努力.某厂改造了10条口罩生产线,每条生产线每天可生产口罩500个.如果每增加一条生产线,每条生产线就会比原来少生产20个口罩.设增加x条生产线后,每条生产线每天可生产口罩y个.
(1)直接写出y与x之间的函数关系式;
(2)设该厂每天可以生产的口罩w个,请求出w与x的函数关系式,并求出增加多少条生产线时,每天生产的口罩数量最多,最多为多少个?
解:(1)由题意可知该函数关系为一次函数,其解析式为:y=500﹣20x;
∴y与x之间的函数关系式为y=500﹣20x(0≤x≤25,且x为整数);
(2)w=(10+x)(500﹣20x)
=﹣20x2+300x+5000
=﹣20(x﹣7.5)2+6125,
∵a=﹣20<0,开口向下,
∴当x=7.5时,w最大,
又∵x为整数,
∴当x=7或8时,w最大,最大值为6120.
答:当增加7或8条生产线时,每天生产的口罩数量最多,为6120个.
23.如图,在Rt△ABC中,∠B=90°,AD平分∠BAC交BC于点D,点E在AC上,以AE为直径的⊙O经过点 D.
(1)求证:BC是⊙O的切线;
(2)若∠C=30°,且CD=3,试求阴影部分的面积.
解:(1)连接OD,
∵AD是∠BAC的平分线,
∴∠DAB=∠DAO,
∵OD=OA,
∴∠DAO=∠ODA,
则∠DAB=∠ODA,
∴DO∥AB,而∠B=90°,
∴∠ODB=90°,
∴BC是⊙O的切线;
(2)连接DE、OD、DF、OF,设圆的半径为R,
∵∠C=30°,CD=3,
∴OD=CD?tan30°=3×=3,
∵∠DAB=∠DAE=30°,
∴=,
∵∠DOE=60°,
∴∠DOF=60°,
∴∠FOA=60°,
∴△OFD、△OFA是等边三角形,
∴DF∥AC,
∴S阴影=S扇形DFO==.
24.△ABC与△CDE都是等边三角形,连接AD、BE.
(1)如图①,当点B、C、D在同一条直线上时,则∠BCE= 120 度;
(2)将图①中的△CDE绕着点C逆时针旋转到如图②的位置.求证:AD=BE.
解:(1)∵△CDE是等边三角形,
∴∠DCE=60°,
∵点B、C、D在同一条直线,
∴∠BCE+∠DCE=180°,
∴∠BCE=180°﹣∠DCE=120°,
故答案为:120;
(2)∵△ABC与△CDE都是等边三角形,
∴BC=AC,CE=CD,∠ACB=∠DCE=60°,
∴∠ACB+∠ACE=∠DCE+∠ACE,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS),
∴BE=AD.
25.如图直角坐标系中,O为坐标原点,抛物线y=﹣x2+6x+3交y轴于点A,过A作AB∥x轴,交抛物线于点B,连接OB.点P为抛物线上AB上方的一个点,连接PA,作PQ⊥AB垂足为H,交OB于点Q.
(1)求AB的长;
(2)当∠APQ=∠B时,求点P的坐标;
(3)当△APH面积是四边形AOQH面积的2倍时,求点P的坐标.
解:(1)对于y=﹣x2+6x+3,令x=0,则y=3,故点A(0,3),
令y=﹣x2+6x+3=3,解得x=0或6,故点B(6,3),
故AB=6;
(2)设P(m,﹣m2+6m+3),
∵∠P=∠B,∠AHP=∠OAB=90°,
∴△ABO~△HPA,故,
∴=,
解得m=4.
∴P(4,11);
(3)当△APH的面积是四边形AOQH的面积的2倍时,
则2(AO+HQ)=PH,
∴2(3+)=﹣m2+6m,
解得:m1=4,m2=3,
∴P(4,11)或P(3,12).
同课章节目录
