2020-2021学年黑龙江省哈尔滨市五常市九年级上学期期末数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年黑龙江省哈尔滨市五常市九年级上学期期末数学试卷(五四学制)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 961.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 07:42:50 | ||
图片预览




文档简介
2020-2021学年黑龙江省哈尔滨市五常市九年级第一学期期末数学试卷(五四学制)
一、选择题(共10小题).
1.若y=(m﹣1)是关于x的二次函数,则m的值为( )
A.﹣2 B.﹣2或1 C.1 D.不存在
2.对于一元二次方程x2+6x﹣11=0,下列说法正确的是( )
A.这个方程有两个相等的实数根
B.这个方程有两个不相等的实数根x1,x2;且x1+x2=﹣6
C.这个方程有两个不相等的实数根x1,x2;且x1+x2=11
D.这个方程没有实数根
3.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
4.有两个事件,事件A:367人中至少有2人生日相同;事件B:抛掷一枚均匀的骰子,朝上的面点数为偶数.下列说法正确的是( )
A.事件A、B都是随机事件
B.事件A、B都是必然事件
C.事件A是随机事件,事件B是必然事件
D.事件A是必然事件,事件B是随机事件
5.如图,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON等于( )
A.11 B.9 C.7 D.5
6.抛物线y=x2﹣5x+3的对称轴是( )
A.x= B.x=﹣ C.x= D.x=﹣
7.某公司2003年缴税60万元,2005年缴税80万元,设该公司这两年缴税的年平均增长率为x,则得到方程( )
A.60+2x=80 B.60(x+1)=80
C.60x2=80 D.60(x+1)2=80
8.如图,△ABC中,点D在AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,连接CD,交EF于点G,则下列说法不正确的是( )
A. B. C. D.
9.下列命题
①垂直于弦的直径平分弦,并且平分弦所对的两条弧;
②在同圆或等圆中相等的圆心角所对的弧相等;
③在同圆或等圆中如果两条弦相等,那么它们所对的圆心角相等;
④圆内接四边形的对角互补.
其中正确的命题共有( )
A.4个 B.3个 C.2个 D.1个
10.如图,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则∠DCF等于( )
A.80° B.50° C.40° D.20°
二、填空题(共10小题).
11.反比例函数y=的图象上,当x<0时,y随x的增大而增大,则m的取值范围是 .
12.高为3米的木箱在地面上的影长为12米,此时测得一建筑物在水面上的影长为36米,则该建筑物的高度为 米.
13.如图,圆O过正方形ABCD的顶点A、D,且与边BC相切,若正方形的边长为2,则圆O的半径为 .
14.一个三角形的两边长分别是3cm和2cm,第三边的长为xcm,若x满足x2﹣3x+2=0,则这个三角形的周长为 cm.
15.春节前夕,小丽的奶奶给孩子们准备了一些红包,这些红包的外观相同,其中有1个红包装的是100元,有3个红包装的是50元,剩下的红包装的是20元.若小丽从中随机拿出一个红包,里面装的是20元的红包的概率是,则装有20元红包的个数是 .
16.把抛物线y=﹣2x2先向右平移1个单位长度,再向上平移2个单位长度后,所得函数的表达式为 .
17.抛物线y=ax2+bx+c与x轴的两个交点坐标分别为(﹣1,0),(3,0),其形状及开口方向与抛物线y=﹣2x2相同,则y=ax2+bx+c的函数解析式为 .
18.一个扇形的圆心角为120°,它的面积是12πcm2,则这个扇形的弧长为 cm.
19.将点A(4,0)绕着原点O顺时针方向旋转30°角到对应点A′,则点A′的坐标是 .
20.如图,等边△ABC的三个顶点在圆O上,BD是直径,则∠BDC= 度,∠BCD= 度,∠ACD= 度.
三、解答题(共60分)
21.解方程:2x2+8x﹣1=0.
22.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).
(1)画出△ABC关于原点O中心对称的△A1B1C1;
(2)分别写出点A1,B1,C1的坐标.
23.已知AB是圆O的直径,点C是圆O上一点,点P为圆O外一点,且OP∥BC,∠P=∠BAC.
(1)求证:PA为圆O的切线;
(2)如果OP=AB=10,求AC的长.
24.甲、乙两同学投掷一枚骰子,用字母p、q分别表示两人各投掷一次的点数.
(1)求满足关于x的方程x2+px+q=0有实数解的概率;
(2)求(1)中方程有两个相同实数解的概率.
25.中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.请判断沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;(精确到0.01)
(参考数据:≈1.414,≈1.732)
26.某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且每件的利润率不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=﹣x+120.
(1)若该服装获得利润为w(元),试写出利润w与销售单价x之间的关系式;销售单价定为多少时,商场可获得利润最大,最大利润是多少元?
(2)若该商场获得利润不低于500元,试确定销售单价x的取值范围.
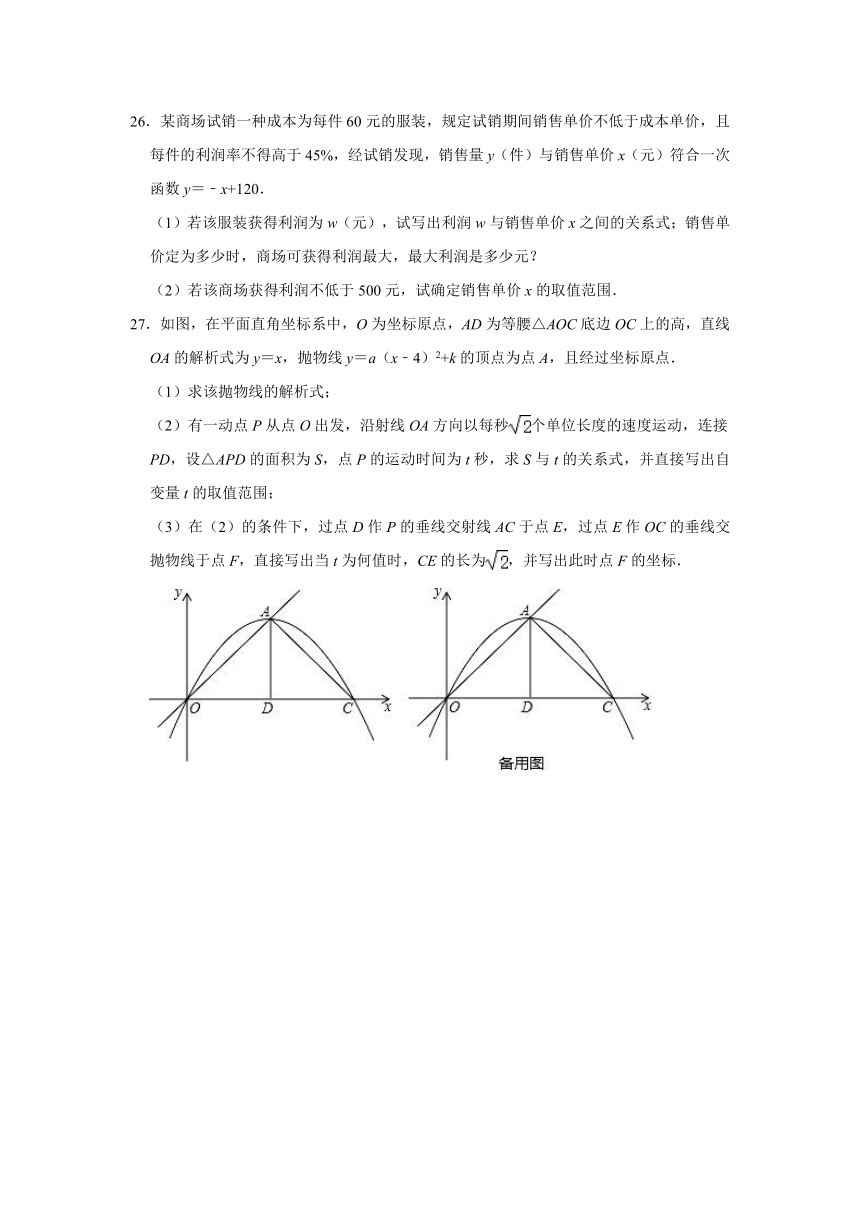
27.如图,在平面直角坐标系中,O为坐标原点,AD为等腰△AOC底边OC上的高,直线OA的解析式为y=x,抛物线y=a(x﹣4)2+k的顶点为点A,且经过坐标原点.
(1)求该抛物线的解析式;
(2)有一动点P从点O出发,沿射线OA方向以每秒个单位长度的速度运动,连接PD,设△APD的面积为S,点P的运动时间为t秒,求S与t的关系式,并直接写出自变量t的取值范围;
(3)在(2)的条件下,过点D作P的垂线交射线AC于点E,过点E作OC的垂线交抛物线于点F,直接写出当t为何值时,CE的长为,并写出此时点F的坐标.
参考答案
一、选择题(共10小题).
1.若y=(m﹣1)是关于x的二次函数,则m的值为( )
A.﹣2 B.﹣2或1 C.1 D.不存在
解:若y=(m﹣1)是关于x的二次函数,则,
解得:m=﹣2.
故选:A.
2.对于一元二次方程x2+6x﹣11=0,下列说法正确的是( )
A.这个方程有两个相等的实数根
B.这个方程有两个不相等的实数根x1,x2;且x1+x2=﹣6
C.这个方程有两个不相等的实数根x1,x2;且x1+x2=11
D.这个方程没有实数根
解:∵x2+6x﹣11=0,
∴△=62﹣4×1×(﹣11)=80>0,
∴这个方程有两个不相等的实数根x1,x2,
且x1+x2=﹣=﹣6,
故选:B.
3.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
解:A、是轴对称图形,也是中心对称图形,故此选项正确;
B、不是轴对称图形,也不是中心对称图形,故此选项错误;
C、是轴对称图形,不是中心对称图形,故此选项错误;
D、不是轴对称图形,是中心对称图形,故此选项错误;
故选:A.
4.有两个事件,事件A:367人中至少有2人生日相同;事件B:抛掷一枚均匀的骰子,朝上的面点数为偶数.下列说法正确的是( )
A.事件A、B都是随机事件
B.事件A、B都是必然事件
C.事件A是随机事件,事件B是必然事件
D.事件A是必然事件,事件B是随机事件
解:事件A、一年最多有366天,所以367人中必有2人的生日相同,是必然事件;
事件B、抛掷一枚均匀的骰子,朝上的面点数为1、2、3、4、5、6共6种情况,点数为偶数是随机事件.
故选:D.
5.如图,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON等于( )
A.11 B.9 C.7 D.5
解:∵ON⊥AB,
∴AN=BN=AB,
∵AB=24,
∴AN=BN=12,
在Rt△OAN中,ON2+AN2=OA2,
∴ON===5,
故选:D.
6.抛物线y=x2﹣5x+3的对称轴是( )
A.x= B.x=﹣ C.x= D.x=﹣
解:∵抛物线y=x2﹣5x+3=(x﹣)2﹣,
∴该抛物线的对称轴是直线x=,
故选:C.
7.某公司2003年缴税60万元,2005年缴税80万元,设该公司这两年缴税的年平均增长率为x,则得到方程( )
A.60+2x=80 B.60(x+1)=80
C.60x2=80 D.60(x+1)2=80
解:设该公司这两年缴税的年平均增长率为x,
依题意得60(x+1)2=80.
故选:D.
8.如图,△ABC中,点D在AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,连接CD,交EF于点G,则下列说法不正确的是( )
A. B. C. D.
解:A、∵EF∥AB,
∴△CGF∽△CDB,
∴=≠,错误,故本选项符合题意;
B、∵DE∥BC,
∴△ADE∽△ABC,
∴=,正确,故本选项不符合题意;
C、∵DE∥BC,
∴△ADE∽△ABC,
∴=,正确,故本选项不符合题意;
D、∵EF∥AB,
∴=,
∵DE∥BC,
∴=,
∴=,正确,故本选项不符合题意;
故选:A.
9.下列命题
①垂直于弦的直径平分弦,并且平分弦所对的两条弧;
②在同圆或等圆中相等的圆心角所对的弧相等;
③在同圆或等圆中如果两条弦相等,那么它们所对的圆心角相等;
④圆内接四边形的对角互补.
其中正确的命题共有( )
A.4个 B.3个 C.2个 D.1个
解:①垂直于弦的直径平分弦,并且平分弦所对的两条弧,本小题说法是真命题;
②在同圆或等圆中相等的圆心角所对的弧相等,本小题说法是真命题;
③在同圆或等圆中如果两条弦相等,那么它们所对的圆心角相等,本小题说法是真命题;
④圆内接四边形的对角互补,本小题说法是真命题;
故选:A.
10.如图,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则∠DCF等于( )
A.80° B.50° C.40° D.20°
解:∵⊙O的直径CD过弦EF的中点G,
∴(垂径定理),
∴∠DCF=∠EOD(等弧所对的圆周角是圆心角的一半),
∴∠DCF=20°.
故选:D.
二、填空题(每题3分,共30分)
11.反比例函数y=的图象上,当x<0时,y随x的增大而增大,则m的取值范围是 m<﹣2 .
解:∵当x<0时,y随x的增大而增大,
∴m+2<0,
解得m<﹣2,
故答案为m<﹣2.
12.高为3米的木箱在地面上的影长为12米,此时测得一建筑物在水面上的影长为36米,则该建筑物的高度为 9 米.
解:∵光线是平行的,影长都在地面上,
∴光线和影长组成的角相等;木箱和建筑物与影长构成的角均为直角,
∴木箱高与影长构成的三角形和建筑物和影长构成的三角形相似,
设树的高度为x米,3:12=x:36,
解得:x=9,
∴该建筑物的高度为9m.
故答案为:9.
13.如图,圆O过正方形ABCD的顶点A、D,且与边BC相切,若正方形的边长为2,则圆O的半径为 .
解:连接OE、OD,延长EO交AD于F,
∴E是切点,
∴OE⊥BC,
∴OF⊥AD,OE=OD;
设OD=x,则OF=2﹣x,
在Rt△ODF中,DF=AD=×2=1,OD=x,OF=2﹣x,
∴x2=(2﹣x)2+12,
解得x=.
故答案为:.
14.一个三角形的两边长分别是3cm和2cm,第三边的长为xcm,若x满足x2﹣3x+2=0,则这个三角形的周长为 7 cm.
解:x2﹣3x+2=0,
(x﹣2)(x﹣1)=0,
∴x﹣2=0或x﹣1=0,
∴x1=2,x2=1,
当x=2时,三角形三边为3,2,2,则三角形的周长=3+2+2=7(cm);
当x=1时,由于1+2=3,不符合三角形三边的关系,舍去.
所以这个三角形的周长为7cm,
故答案为7.
15.春节前夕,小丽的奶奶给孩子们准备了一些红包,这些红包的外观相同,其中有1个红包装的是100元,有3个红包装的是50元,剩下的红包装的是20元.若小丽从中随机拿出一个红包,里面装的是20元的红包的概率是,则装有20元红包的个数是 16 .
解:设有20元的红包x个,根据题意得:=,
解得:x=16,
故答案为:16.
16.把抛物线y=﹣2x2先向右平移1个单位长度,再向上平移2个单位长度后,所得函数的表达式为 y=﹣2(x﹣1)2+2 .
解:抛物线y=﹣2x2向右平移1个单位长度所得解析式为:y=﹣2(x﹣1)2,
再向上平移2个单位长度后,所得函数的表达式为:y=﹣2(x﹣1)2+2.
故答案为:y=﹣2(x﹣1)2+2.
17.抛物线y=ax2+bx+c与x轴的两个交点坐标分别为(﹣1,0),(3,0),其形状及开口方向与抛物线y=﹣2x2相同,则y=ax2+bx+c的函数解析式为 y=﹣2x2+4x+6 .
解:根据题意a=﹣2,
∵抛物线y=ax2+bx+c与x轴的两个交点坐标分别为(﹣1,0),(3,0),
∴该抛物线解析式是y=﹣2(x+1)(x﹣3),即y=﹣2x2+4x+6.
故答案是:y=﹣2x2+4x+6.
18.一个扇形的圆心角为120°,它的面积是12πcm2,则这个扇形的弧长为 4π cm.
解:设扇形的半径为r,
∵扇形的圆心角是120°,面积是12πcm2,
∴=12π,解得r=6,
∴扇形的弧长==4π(cm).
故答案为:4π.
19.将点A(4,0)绕着原点O顺时针方向旋转30°角到对应点A′,则点A′的坐标是 (2,﹣2) .
解:
作A′B⊥x轴于点B,
∵OA′=OA=4,∠AOA′=30°,
∴A′B=OA′=2,OB=OA×cos30°=2.
故答案为:A′(2,﹣2).
20.如图,等边△ABC的三个顶点在圆O上,BD是直径,则∠BDC= 60 度,∠BCD= 90 度,∠ACD= 30 度.
解:∵△ABC为等边三角形,
∴∠A=∠ACB=60°,
∴∠BDC=∠A=60°,
∵BD为直径,
∴∠BCD=90°,
∴∠ACD=∠BCD﹣∠ACB=90°﹣60°=30°.
故答案为60,90,30.
三、解答题(共60分)
21.解方程:2x2+8x﹣1=0.
解:2x2+8x﹣1=0,
x2+4x=,
x2+4x+4=+4,即(x+2)2=,
∴x+2=±,
则x1=﹣2+,x2=﹣2﹣.
22.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).
(1)画出△ABC关于原点O中心对称的△A1B1C1;
(2)分别写出点A1,B1,C1的坐标.
解:(1)如图,△A1B1C1为所作;
(2)A1(2,﹣1),B1(4,﹣5),C1(5,﹣2).
23.已知AB是圆O的直径,点C是圆O上一点,点P为圆O外一点,且OP∥BC,∠P=∠BAC.
(1)求证:PA为圆O的切线;
(2)如果OP=AB=10,求AC的长.
【解答】(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC+∠B=90°,
又∵OP∥BC,
∴∠AOP=∠B,
∴∠BAC+∠AOP=90°,
∵∠P=∠BAC,
∴∠P+∠AOP=90°,
∴∠PAO=90°,
∴PA⊥OA,
又∵OA是的⊙O的半径,
∴PA为⊙O的切线;
(2)解:由(1)得:∠PAO=∠ACB=90°,
又∵∠P=∠BAC,OP=BA,
∴△OAP≌△BCA(AAS),
∴BC=OA=AB=5,
∴AC===5
24.甲、乙两同学投掷一枚骰子,用字母p、q分别表示两人各投掷一次的点数.
(1)求满足关于x的方程x2+px+q=0有实数解的概率;
(2)求(1)中方程有两个相同实数解的概率.
解:两人投掷骰子共有36种等可能情况,
(1)其中使方程有实数解共有19种情况:
p=6时,q=6、5、4、3、2、1;
p=5时,q=6、5、4、3、2、1;
p=4时,q=4、3、2、1;
p=3时,q=2、1;
p=2时,q=1;故其概率为.
(2)使方程有相等实数解共有2种情况:
p=4,q=4;p=2,q=1;故其概率为.
25.中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.请判断沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;(精确到0.01)
(参考数据:≈1.414,≈1.732)
解:(1)过点C作CD垂直AB延长线于点D,
设CD=x米,
在Rt△ACD中,
∵∠DAC=45°,
∴AD=x,
在Rt△BCD中,
∵∠CBD=60°,
∴BD=x,
∴AB=AD﹣BD=x﹣x=2000,
解得:x≈4732,
∴船C距离海平面为4732+1800=6532米<7062.68米,
∴沉船C在“蛟龙”号深潜极限范围内.
26.某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且每件的利润率不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=﹣x+120.
(1)若该服装获得利润为w(元),试写出利润w与销售单价x之间的关系式;销售单价定为多少时,商场可获得利润最大,最大利润是多少元?
(2)若该商场获得利润不低于500元,试确定销售单价x的取值范围.
解:(1)由题意得:
w=(﹣x+120)(x﹣60)
=﹣x2+180x﹣7200
=﹣(x﹣90)2+900,
∵二次项系数为负,抛物线开口向下,
∴当x≤90时,w随x的增大而增大,
∵销售单价不低于成本单价,且每件的利润率不得高于45%,
∴60≤x≤45%×60+60,
即60≤x≤87,
∴当x=87时,商场可获得最大利润,
此时,w=﹣(87﹣90)2+900=891(元).
∴利润w与销售单价x之间的关系式为w=﹣x2+180x﹣7200;销售单价定为87元时,商场可获得利润最大,最大利润是891元.
(2)当w=500时,则有:500=﹣x2+180x﹣7200,
整理得:x2﹣180x+7700=0,
解得:x1=70,x2=110,
∵抛物线开口向下,对称轴为直线x=90,
∴若该商场获得利润不低于500元,则有70≤x≤110,
又∵60≤x≤87,
∴销售单价x的取值范围为:70≤x≤87.
27.如图,在平面直角坐标系中,O为坐标原点,AD为等腰△AOC底边OC上的高,直线OA的解析式为y=x,抛物线y=a(x﹣4)2+k的顶点为点A,且经过坐标原点.
(1)求该抛物线的解析式;
(2)有一动点P从点O出发,沿射线OA方向以每秒个单位长度的速度运动,连接PD,设△APD的面积为S,点P的运动时间为t秒,求S与t的关系式,并直接写出自变量t的取值范围;
(3)在(2)的条件下,过点D作P的垂线交射线AC于点E,过点E作OC的垂线交抛物线于点F,直接写出当t为何值时,CE的长为,并写出此时点F的坐标.
解:(1)∵抛物线y=a(x﹣4)2+k的顶点为A,
∴A的横坐标为4.
又∵直线OA的解析式为y=x,
∴当x=4时,y=4.
∴点A的坐标为(4,4).
将(4,4),(0,0)代入y=a(x﹣4)2+k得;a=﹣,
∴k=4.
∴抛物线的解析式为y=﹣x2+2x.
(2)当点P在线段OA上时,如图1所示,过点P作PM⊥AD于点M.
∵AD为等腰三角形AOC底边OC上的高,
∴∠PAD=45°.
∴PM=AP?sin∠PAD=(4﹣2t).
∴S△APD=AD?PM=×4××(4﹣t)=8﹣2t(0≤t<4).
当点P在线段OA的延长线上时,如图2所示,过点P作PM⊥AD于点M.
∵∠PAM=45°,
∴PM=AP?sin∠PAM=(t﹣4).
∴S△APD=AD?PM=×4×(t﹣4)=2t﹣8(t>4).
∴S与t的函数关系式为S=.
(3)如图3所示:
∵PD⊥DE,
∴∠ADP=∠EDC.
在△PAD和△ECD中,
,
∴△PAD≌△ECD(ASA).
∴AP=EC=.
∴4﹣t=.
解得:t=3.
设EF交x轴于点N,在Rt△CEN中,∠ECN=45°,CE=,
∴CN=CEcos∠ECN=×=1.
∴ON=7.
将x=7代入抛物线的解析式得:y=﹣×72+2×7=.
∴点F的坐标为(7,).
如图4所示:
∵PD⊥DE,
∴∠ADP=∠EDC.
在△PAD和△ECD中,
,
∴△PAD≌△ECD(ASA).
∴AP=EC=.
∴t﹣4=.
解得:t=5.
设EF交x轴于点N,在Rt△CEN中,∠ECN=45°,CE=,
∴CN=CEcos∠ECN=×=1.
∴ON=9.
将x=9代入抛物线的解析式得:y=﹣×92+2×9=﹣.
∴点F的坐标为(9,﹣).
综上所述,点F的坐标为(7,)或(9,﹣).
一、选择题(共10小题).
1.若y=(m﹣1)是关于x的二次函数,则m的值为( )
A.﹣2 B.﹣2或1 C.1 D.不存在
2.对于一元二次方程x2+6x﹣11=0,下列说法正确的是( )
A.这个方程有两个相等的实数根
B.这个方程有两个不相等的实数根x1,x2;且x1+x2=﹣6
C.这个方程有两个不相等的实数根x1,x2;且x1+x2=11
D.这个方程没有实数根
3.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
4.有两个事件,事件A:367人中至少有2人生日相同;事件B:抛掷一枚均匀的骰子,朝上的面点数为偶数.下列说法正确的是( )
A.事件A、B都是随机事件
B.事件A、B都是必然事件
C.事件A是随机事件,事件B是必然事件
D.事件A是必然事件,事件B是随机事件
5.如图,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON等于( )
A.11 B.9 C.7 D.5
6.抛物线y=x2﹣5x+3的对称轴是( )
A.x= B.x=﹣ C.x= D.x=﹣
7.某公司2003年缴税60万元,2005年缴税80万元,设该公司这两年缴税的年平均增长率为x,则得到方程( )
A.60+2x=80 B.60(x+1)=80
C.60x2=80 D.60(x+1)2=80
8.如图,△ABC中,点D在AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,连接CD,交EF于点G,则下列说法不正确的是( )
A. B. C. D.
9.下列命题
①垂直于弦的直径平分弦,并且平分弦所对的两条弧;
②在同圆或等圆中相等的圆心角所对的弧相等;
③在同圆或等圆中如果两条弦相等,那么它们所对的圆心角相等;
④圆内接四边形的对角互补.
其中正确的命题共有( )
A.4个 B.3个 C.2个 D.1个
10.如图,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则∠DCF等于( )
A.80° B.50° C.40° D.20°
二、填空题(共10小题).
11.反比例函数y=的图象上,当x<0时,y随x的增大而增大,则m的取值范围是 .
12.高为3米的木箱在地面上的影长为12米,此时测得一建筑物在水面上的影长为36米,则该建筑物的高度为 米.
13.如图,圆O过正方形ABCD的顶点A、D,且与边BC相切,若正方形的边长为2,则圆O的半径为 .
14.一个三角形的两边长分别是3cm和2cm,第三边的长为xcm,若x满足x2﹣3x+2=0,则这个三角形的周长为 cm.
15.春节前夕,小丽的奶奶给孩子们准备了一些红包,这些红包的外观相同,其中有1个红包装的是100元,有3个红包装的是50元,剩下的红包装的是20元.若小丽从中随机拿出一个红包,里面装的是20元的红包的概率是,则装有20元红包的个数是 .
16.把抛物线y=﹣2x2先向右平移1个单位长度,再向上平移2个单位长度后,所得函数的表达式为 .
17.抛物线y=ax2+bx+c与x轴的两个交点坐标分别为(﹣1,0),(3,0),其形状及开口方向与抛物线y=﹣2x2相同,则y=ax2+bx+c的函数解析式为 .
18.一个扇形的圆心角为120°,它的面积是12πcm2,则这个扇形的弧长为 cm.
19.将点A(4,0)绕着原点O顺时针方向旋转30°角到对应点A′,则点A′的坐标是 .
20.如图,等边△ABC的三个顶点在圆O上,BD是直径,则∠BDC= 度,∠BCD= 度,∠ACD= 度.
三、解答题(共60分)
21.解方程:2x2+8x﹣1=0.
22.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).
(1)画出△ABC关于原点O中心对称的△A1B1C1;
(2)分别写出点A1,B1,C1的坐标.
23.已知AB是圆O的直径,点C是圆O上一点,点P为圆O外一点,且OP∥BC,∠P=∠BAC.
(1)求证:PA为圆O的切线;
(2)如果OP=AB=10,求AC的长.
24.甲、乙两同学投掷一枚骰子,用字母p、q分别表示两人各投掷一次的点数.
(1)求满足关于x的方程x2+px+q=0有实数解的概率;
(2)求(1)中方程有两个相同实数解的概率.
25.中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.请判断沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;(精确到0.01)
(参考数据:≈1.414,≈1.732)
26.某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且每件的利润率不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=﹣x+120.
(1)若该服装获得利润为w(元),试写出利润w与销售单价x之间的关系式;销售单价定为多少时,商场可获得利润最大,最大利润是多少元?
(2)若该商场获得利润不低于500元,试确定销售单价x的取值范围.
27.如图,在平面直角坐标系中,O为坐标原点,AD为等腰△AOC底边OC上的高,直线OA的解析式为y=x,抛物线y=a(x﹣4)2+k的顶点为点A,且经过坐标原点.
(1)求该抛物线的解析式;
(2)有一动点P从点O出发,沿射线OA方向以每秒个单位长度的速度运动,连接PD,设△APD的面积为S,点P的运动时间为t秒,求S与t的关系式,并直接写出自变量t的取值范围;
(3)在(2)的条件下,过点D作P的垂线交射线AC于点E,过点E作OC的垂线交抛物线于点F,直接写出当t为何值时,CE的长为,并写出此时点F的坐标.
参考答案
一、选择题(共10小题).
1.若y=(m﹣1)是关于x的二次函数,则m的值为( )
A.﹣2 B.﹣2或1 C.1 D.不存在
解:若y=(m﹣1)是关于x的二次函数,则,
解得:m=﹣2.
故选:A.
2.对于一元二次方程x2+6x﹣11=0,下列说法正确的是( )
A.这个方程有两个相等的实数根
B.这个方程有两个不相等的实数根x1,x2;且x1+x2=﹣6
C.这个方程有两个不相等的实数根x1,x2;且x1+x2=11
D.这个方程没有实数根
解:∵x2+6x﹣11=0,
∴△=62﹣4×1×(﹣11)=80>0,
∴这个方程有两个不相等的实数根x1,x2,
且x1+x2=﹣=﹣6,
故选:B.
3.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
解:A、是轴对称图形,也是中心对称图形,故此选项正确;
B、不是轴对称图形,也不是中心对称图形,故此选项错误;
C、是轴对称图形,不是中心对称图形,故此选项错误;
D、不是轴对称图形,是中心对称图形,故此选项错误;
故选:A.
4.有两个事件,事件A:367人中至少有2人生日相同;事件B:抛掷一枚均匀的骰子,朝上的面点数为偶数.下列说法正确的是( )
A.事件A、B都是随机事件
B.事件A、B都是必然事件
C.事件A是随机事件,事件B是必然事件
D.事件A是必然事件,事件B是随机事件
解:事件A、一年最多有366天,所以367人中必有2人的生日相同,是必然事件;
事件B、抛掷一枚均匀的骰子,朝上的面点数为1、2、3、4、5、6共6种情况,点数为偶数是随机事件.
故选:D.
5.如图,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON等于( )
A.11 B.9 C.7 D.5
解:∵ON⊥AB,
∴AN=BN=AB,
∵AB=24,
∴AN=BN=12,
在Rt△OAN中,ON2+AN2=OA2,
∴ON===5,
故选:D.
6.抛物线y=x2﹣5x+3的对称轴是( )
A.x= B.x=﹣ C.x= D.x=﹣
解:∵抛物线y=x2﹣5x+3=(x﹣)2﹣,
∴该抛物线的对称轴是直线x=,
故选:C.
7.某公司2003年缴税60万元,2005年缴税80万元,设该公司这两年缴税的年平均增长率为x,则得到方程( )
A.60+2x=80 B.60(x+1)=80
C.60x2=80 D.60(x+1)2=80
解:设该公司这两年缴税的年平均增长率为x,
依题意得60(x+1)2=80.
故选:D.
8.如图,△ABC中,点D在AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,连接CD,交EF于点G,则下列说法不正确的是( )
A. B. C. D.
解:A、∵EF∥AB,
∴△CGF∽△CDB,
∴=≠,错误,故本选项符合题意;
B、∵DE∥BC,
∴△ADE∽△ABC,
∴=,正确,故本选项不符合题意;
C、∵DE∥BC,
∴△ADE∽△ABC,
∴=,正确,故本选项不符合题意;
D、∵EF∥AB,
∴=,
∵DE∥BC,
∴=,
∴=,正确,故本选项不符合题意;
故选:A.
9.下列命题
①垂直于弦的直径平分弦,并且平分弦所对的两条弧;
②在同圆或等圆中相等的圆心角所对的弧相等;
③在同圆或等圆中如果两条弦相等,那么它们所对的圆心角相等;
④圆内接四边形的对角互补.
其中正确的命题共有( )
A.4个 B.3个 C.2个 D.1个
解:①垂直于弦的直径平分弦,并且平分弦所对的两条弧,本小题说法是真命题;
②在同圆或等圆中相等的圆心角所对的弧相等,本小题说法是真命题;
③在同圆或等圆中如果两条弦相等,那么它们所对的圆心角相等,本小题说法是真命题;
④圆内接四边形的对角互补,本小题说法是真命题;
故选:A.
10.如图,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则∠DCF等于( )
A.80° B.50° C.40° D.20°
解:∵⊙O的直径CD过弦EF的中点G,
∴(垂径定理),
∴∠DCF=∠EOD(等弧所对的圆周角是圆心角的一半),
∴∠DCF=20°.
故选:D.
二、填空题(每题3分,共30分)
11.反比例函数y=的图象上,当x<0时,y随x的增大而增大,则m的取值范围是 m<﹣2 .
解:∵当x<0时,y随x的增大而增大,
∴m+2<0,
解得m<﹣2,
故答案为m<﹣2.
12.高为3米的木箱在地面上的影长为12米,此时测得一建筑物在水面上的影长为36米,则该建筑物的高度为 9 米.
解:∵光线是平行的,影长都在地面上,
∴光线和影长组成的角相等;木箱和建筑物与影长构成的角均为直角,
∴木箱高与影长构成的三角形和建筑物和影长构成的三角形相似,
设树的高度为x米,3:12=x:36,
解得:x=9,
∴该建筑物的高度为9m.
故答案为:9.
13.如图,圆O过正方形ABCD的顶点A、D,且与边BC相切,若正方形的边长为2,则圆O的半径为 .
解:连接OE、OD,延长EO交AD于F,
∴E是切点,
∴OE⊥BC,
∴OF⊥AD,OE=OD;
设OD=x,则OF=2﹣x,
在Rt△ODF中,DF=AD=×2=1,OD=x,OF=2﹣x,
∴x2=(2﹣x)2+12,
解得x=.
故答案为:.
14.一个三角形的两边长分别是3cm和2cm,第三边的长为xcm,若x满足x2﹣3x+2=0,则这个三角形的周长为 7 cm.
解:x2﹣3x+2=0,
(x﹣2)(x﹣1)=0,
∴x﹣2=0或x﹣1=0,
∴x1=2,x2=1,
当x=2时,三角形三边为3,2,2,则三角形的周长=3+2+2=7(cm);
当x=1时,由于1+2=3,不符合三角形三边的关系,舍去.
所以这个三角形的周长为7cm,
故答案为7.
15.春节前夕,小丽的奶奶给孩子们准备了一些红包,这些红包的外观相同,其中有1个红包装的是100元,有3个红包装的是50元,剩下的红包装的是20元.若小丽从中随机拿出一个红包,里面装的是20元的红包的概率是,则装有20元红包的个数是 16 .
解:设有20元的红包x个,根据题意得:=,
解得:x=16,
故答案为:16.
16.把抛物线y=﹣2x2先向右平移1个单位长度,再向上平移2个单位长度后,所得函数的表达式为 y=﹣2(x﹣1)2+2 .
解:抛物线y=﹣2x2向右平移1个单位长度所得解析式为:y=﹣2(x﹣1)2,
再向上平移2个单位长度后,所得函数的表达式为:y=﹣2(x﹣1)2+2.
故答案为:y=﹣2(x﹣1)2+2.
17.抛物线y=ax2+bx+c与x轴的两个交点坐标分别为(﹣1,0),(3,0),其形状及开口方向与抛物线y=﹣2x2相同,则y=ax2+bx+c的函数解析式为 y=﹣2x2+4x+6 .
解:根据题意a=﹣2,
∵抛物线y=ax2+bx+c与x轴的两个交点坐标分别为(﹣1,0),(3,0),
∴该抛物线解析式是y=﹣2(x+1)(x﹣3),即y=﹣2x2+4x+6.
故答案是:y=﹣2x2+4x+6.
18.一个扇形的圆心角为120°,它的面积是12πcm2,则这个扇形的弧长为 4π cm.
解:设扇形的半径为r,
∵扇形的圆心角是120°,面积是12πcm2,
∴=12π,解得r=6,
∴扇形的弧长==4π(cm).
故答案为:4π.
19.将点A(4,0)绕着原点O顺时针方向旋转30°角到对应点A′,则点A′的坐标是 (2,﹣2) .
解:
作A′B⊥x轴于点B,
∵OA′=OA=4,∠AOA′=30°,
∴A′B=OA′=2,OB=OA×cos30°=2.
故答案为:A′(2,﹣2).
20.如图,等边△ABC的三个顶点在圆O上,BD是直径,则∠BDC= 60 度,∠BCD= 90 度,∠ACD= 30 度.
解:∵△ABC为等边三角形,
∴∠A=∠ACB=60°,
∴∠BDC=∠A=60°,
∵BD为直径,
∴∠BCD=90°,
∴∠ACD=∠BCD﹣∠ACB=90°﹣60°=30°.
故答案为60,90,30.
三、解答题(共60分)
21.解方程:2x2+8x﹣1=0.
解:2x2+8x﹣1=0,
x2+4x=,
x2+4x+4=+4,即(x+2)2=,
∴x+2=±,
则x1=﹣2+,x2=﹣2﹣.
22.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).
(1)画出△ABC关于原点O中心对称的△A1B1C1;
(2)分别写出点A1,B1,C1的坐标.
解:(1)如图,△A1B1C1为所作;
(2)A1(2,﹣1),B1(4,﹣5),C1(5,﹣2).
23.已知AB是圆O的直径,点C是圆O上一点,点P为圆O外一点,且OP∥BC,∠P=∠BAC.
(1)求证:PA为圆O的切线;
(2)如果OP=AB=10,求AC的长.
【解答】(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC+∠B=90°,
又∵OP∥BC,
∴∠AOP=∠B,
∴∠BAC+∠AOP=90°,
∵∠P=∠BAC,
∴∠P+∠AOP=90°,
∴∠PAO=90°,
∴PA⊥OA,
又∵OA是的⊙O的半径,
∴PA为⊙O的切线;
(2)解:由(1)得:∠PAO=∠ACB=90°,
又∵∠P=∠BAC,OP=BA,
∴△OAP≌△BCA(AAS),
∴BC=OA=AB=5,
∴AC===5
24.甲、乙两同学投掷一枚骰子,用字母p、q分别表示两人各投掷一次的点数.
(1)求满足关于x的方程x2+px+q=0有实数解的概率;
(2)求(1)中方程有两个相同实数解的概率.
解:两人投掷骰子共有36种等可能情况,
(1)其中使方程有实数解共有19种情况:
p=6时,q=6、5、4、3、2、1;
p=5时,q=6、5、4、3、2、1;
p=4时,q=4、3、2、1;
p=3时,q=2、1;
p=2时,q=1;故其概率为.
(2)使方程有相等实数解共有2种情况:
p=4,q=4;p=2,q=1;故其概率为.
25.中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.请判断沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;(精确到0.01)
(参考数据:≈1.414,≈1.732)
解:(1)过点C作CD垂直AB延长线于点D,
设CD=x米,
在Rt△ACD中,
∵∠DAC=45°,
∴AD=x,
在Rt△BCD中,
∵∠CBD=60°,
∴BD=x,
∴AB=AD﹣BD=x﹣x=2000,
解得:x≈4732,
∴船C距离海平面为4732+1800=6532米<7062.68米,
∴沉船C在“蛟龙”号深潜极限范围内.
26.某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且每件的利润率不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=﹣x+120.
(1)若该服装获得利润为w(元),试写出利润w与销售单价x之间的关系式;销售单价定为多少时,商场可获得利润最大,最大利润是多少元?
(2)若该商场获得利润不低于500元,试确定销售单价x的取值范围.
解:(1)由题意得:
w=(﹣x+120)(x﹣60)
=﹣x2+180x﹣7200
=﹣(x﹣90)2+900,
∵二次项系数为负,抛物线开口向下,
∴当x≤90时,w随x的增大而增大,
∵销售单价不低于成本单价,且每件的利润率不得高于45%,
∴60≤x≤45%×60+60,
即60≤x≤87,
∴当x=87时,商场可获得最大利润,
此时,w=﹣(87﹣90)2+900=891(元).
∴利润w与销售单价x之间的关系式为w=﹣x2+180x﹣7200;销售单价定为87元时,商场可获得利润最大,最大利润是891元.
(2)当w=500时,则有:500=﹣x2+180x﹣7200,
整理得:x2﹣180x+7700=0,
解得:x1=70,x2=110,
∵抛物线开口向下,对称轴为直线x=90,
∴若该商场获得利润不低于500元,则有70≤x≤110,
又∵60≤x≤87,
∴销售单价x的取值范围为:70≤x≤87.
27.如图,在平面直角坐标系中,O为坐标原点,AD为等腰△AOC底边OC上的高,直线OA的解析式为y=x,抛物线y=a(x﹣4)2+k的顶点为点A,且经过坐标原点.
(1)求该抛物线的解析式;
(2)有一动点P从点O出发,沿射线OA方向以每秒个单位长度的速度运动,连接PD,设△APD的面积为S,点P的运动时间为t秒,求S与t的关系式,并直接写出自变量t的取值范围;
(3)在(2)的条件下,过点D作P的垂线交射线AC于点E,过点E作OC的垂线交抛物线于点F,直接写出当t为何值时,CE的长为,并写出此时点F的坐标.
解:(1)∵抛物线y=a(x﹣4)2+k的顶点为A,
∴A的横坐标为4.
又∵直线OA的解析式为y=x,
∴当x=4时,y=4.
∴点A的坐标为(4,4).
将(4,4),(0,0)代入y=a(x﹣4)2+k得;a=﹣,
∴k=4.
∴抛物线的解析式为y=﹣x2+2x.
(2)当点P在线段OA上时,如图1所示,过点P作PM⊥AD于点M.
∵AD为等腰三角形AOC底边OC上的高,
∴∠PAD=45°.
∴PM=AP?sin∠PAD=(4﹣2t).
∴S△APD=AD?PM=×4××(4﹣t)=8﹣2t(0≤t<4).
当点P在线段OA的延长线上时,如图2所示,过点P作PM⊥AD于点M.
∵∠PAM=45°,
∴PM=AP?sin∠PAM=(t﹣4).
∴S△APD=AD?PM=×4×(t﹣4)=2t﹣8(t>4).
∴S与t的函数关系式为S=.
(3)如图3所示:
∵PD⊥DE,
∴∠ADP=∠EDC.
在△PAD和△ECD中,
,
∴△PAD≌△ECD(ASA).
∴AP=EC=.
∴4﹣t=.
解得:t=3.
设EF交x轴于点N,在Rt△CEN中,∠ECN=45°,CE=,
∴CN=CEcos∠ECN=×=1.
∴ON=7.
将x=7代入抛物线的解析式得:y=﹣×72+2×7=.
∴点F的坐标为(7,).
如图4所示:
∵PD⊥DE,
∴∠ADP=∠EDC.
在△PAD和△ECD中,
,
∴△PAD≌△ECD(ASA).
∴AP=EC=.
∴t﹣4=.
解得:t=5.
设EF交x轴于点N,在Rt△CEN中,∠ECN=45°,CE=,
∴CN=CEcos∠ECN=×=1.
∴ON=9.
将x=9代入抛物线的解析式得:y=﹣×92+2×9=﹣.
∴点F的坐标为(9,﹣).
综上所述,点F的坐标为(7,)或(9,﹣).
同课章节目录
