2011中考冲刺数学专题2-探索型问题
文档属性
| 名称 | 2011中考冲刺数学专题2-探索型问题 |

|
|
| 格式 | zip | ||
| 文件大小 | 410.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 新人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-20 00:00:00 | ||
图片预览




文档简介
2011中考冲刺数学专题2—— 探索型问题
【备考点睛】
探索型问题是指那些条件不完备、结论不明确、或答案不唯一、给学生留有较大探索余地的试题。从最近几年来中考中探索性问题逐年攀升的趋势,可预测探索性问题仍将是中考命题“孜孜以求的目标”。
探索型问题一般有两类:
(1)探索条件的开放题;(2)探索结论的开放题。
探索型问题的特点:
(1)题设开放型探索性问题的特点是给出结论,不给出条件或条件残缺,需在给定结论的前提下,探索结论成立的条件,但满足结论成立的条件往往不唯一,答案与已知条件对整个问题而言只要是充分的、相容的、独立的,就视为正确的;
(2)结论开放型探索性问题的特点是给出一定的条件而未给出结论,要求在给定的前提条件下,探索结论的多样性,然后通过推理证明确定结论;
【经典例题】
类型一 条件开放型问题
例题1.(2010福建宁德)如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.
⑴ 求证:△AMB≌△ENB;
⑵ ①当M点在何处时,AM+CM的值最小;
②当M点在何处时,AM+BM+CM的值最小,并说明理由;
⑶ 当AM+BM+CM的最小值为时,求正方形的边长.
解答:⑴∵△ABE是等边三角形,
∴BA=BE,∠ABE=60°.
∵∠MBN=60°,
∴∠MBN-∠ABN=∠ABE-∠ABN.
即∠BMA=∠NBE.
又∵MB=NB,
∴△AMB≌△ENB(SAS).
⑵①当M点落在BD的中点时,AM+CM的值最小.
②如图,连接CE,当M点位于BD与CE的交点处时,
AM+BM+CM的值最小.
理由如下:连接MN.由⑴知,△AMB≌△ENB,
∴AM=EN.
∵∠MBN=60°,MB=NB,
∴△BMN是等边三角形.
∴BM=MN.
∴AM+BM+CM=EN+MN+CM.
根据“两点之间线段最短”,得EN+MN+CM=EC最短
∴当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长.
⑶过E点作EF⊥BC交CB的延长线于F,
∴∠EBF=90°-60°=30°.
设正方形的边长为x,则BF=x,EF=.
在Rt△EFC中,
∵EF2+FC2=EC2,
∴()2+(x+x)2=.
解得,x=(舍去负值).
∴正方形的边长为.
例题2.如图,四边形ABCD是平行四边形.O是对角线AC的中点,过点O的直线EF分别交AB、DC于点E、F,与CB、AD的延长线分别交于点G、H.
(1)写出图中不全等的两个相似三角形(不要求证明);
(2)除AB=CD,AD=BC,OA=OC这三对相等的线段外,图中还有多对相等的线段,请选出其中一对加以证明.
解答:分析:考察了相似的两种基本图形,平行四边形中利用全等三角形的简单证明.
(1) AEH与DFH.(或AEH与BEG, 或BEG与CFG ,或DFH与CFG)
(2)OE=OF.
证明:四边形ABCD是平行四边形,
∥CD, ,
, △△,
.
例题3.(2010 甘肃)如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标;
(2)以B、C、D为顶点的三角形是直角三角形吗?为什么?
(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,请指出符合条件的点P的位置,并直接写出点P的坐标;若不存在,请说明理由.
解答:(1)设该抛物线的解析式为,
由抛物线与y轴交于点C(0,-3),可知.
即抛物线的解析式为.
把A(-1,0)、B(3,0)代入, 得
解得.
∴ 抛物线的解析式为y = x2-2x-3.
∴ 顶点D的坐标为.
(2)以B、C、D为顶点的三角形是直角三角形.
理由如下:
过点D分别作轴、轴的垂线,垂足分别为E、F.
在Rt△BOC中,OB=3,OC=3,∴ .
在Rt△CDF中,DF=1,CF=OF-OC=4-3=1,∴ .
在Rt△BDE中,DE=4,BE=OB-OE=3-1=2,∴ .
∴ , 故△BCD为直角三角形.
(3)连接AC,可知Rt△COA∽ Rt△BCD,
得符合条件的点为O(0,0).
过A作AP1⊥AC交y轴正半轴于P1,
可知Rt△CAP1 ∽ Rt△COA∽ Rt△BCD,
求得符合条件的点为.
过C作CP2⊥AC交x轴正半轴于P2,
可知Rt△P2CA∽ Rt△COA∽ Rt△BCD,
求得符合条件的点为P2(9,0).
∴符合条件的点有三个:
O(0,0),,P2(9,0).
类型二 结论开放型问题
例题4.(2010四川眉山)如图,Rt△AB C 是由Rt△ABC绕点A顺时针旋转得到的,连结CC 交斜边于点E,CC 的延长线交BB 于点F.
(1)证明:△ACE∽△FBE;
(2)设∠ABC=,∠CAC =,试探索
、满足什么关系时,△ACE与△FBE
是全等三角形,并说明理由.
解答:(1)证明:∵Rt△AB C 是由Rt△ABC绕
点A顺时针旋转得到的,
∴AC=AC ,AB=AB ,∠CAB=∠C AB
∴∠CAC =∠BAB
∴∠ACC =∠ABB
又∠AEC=∠FEB
∴△ACE∽△FBE
(2)解:当时,△ACE≌△FBE.
在△ACC中,∵AC=AC ,
∴
在Rt△ABC中,
∠ACC+∠BCE=90°,即,
∴∠BCE=.
∵∠ABC=,
∴∠ABC=∠BCE
∴CE=BE
由(1)知:△ACE∽△FBE,
∴△ACE≌△FBE.
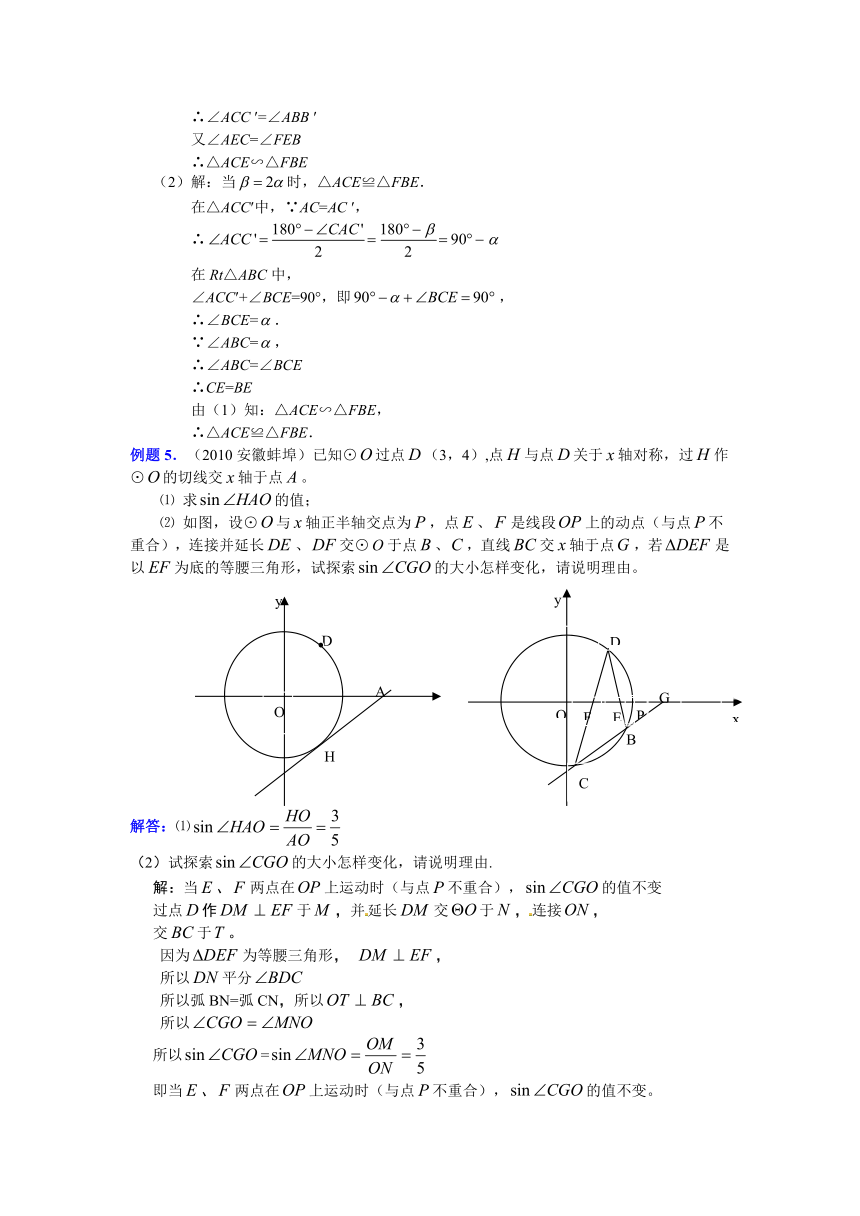
例题5.(2010安徽蚌埠)已知⊙过点(3,4),点与点关于轴对称,过作⊙的切线交轴于点。
⑴ 求的值;
⑵ 如图,设⊙与轴正半轴交点为,点、是线段上的动点(与点不重合),连接并延长、交⊙于点、,直线交轴于点,若是以为底的等腰三角形,试探索的大小怎样变化,请说明理由。
解答:⑴
(2)试探索的大小怎样变化,请说明理由.
解:当、两点在上运动时(与点不重合),的值不变
过点作于,并延长交于,连接,
交于。
因为为等腰三角形, ,
所以平分
所以弧BN=弧CN,所以,
所以
所以=
即当、两点在上运动时(与点不重合),的值不变。
例题6.某天,小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.下图中线段AB、OB分别表示父、子俩送票、取票过程中,离体育馆的路程S(米)与所用时间(分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
(1)求点B的坐标和AB所在直线的函数关系式;
(2)小明能否在比赛开始前到达体育馆?
解答: 从函数图象中“读图找点”,由点的坐标找数量,利用列算式或方程求解,也可以“见形想式”,通过建立函数关系式,利用函数求解。
【解答】(1)解法一:从图象可以看出:父子俩从出发到相遇时花费了15分钟 设小明步行的速度为x米/分,则小明父亲骑车的速度为3x米/分
依题意得:15x+45x=3600. 解得:x=60.
所以两人相遇处离体育馆的距离为60×15=900米.
所以点B的坐标为(15,900).
设直线AB的函数关系式为S=kt+b(k≠0).
由题意,直线AB经过点A(0,3600)、B(15,900)得:解之,得
∴直线AB的函数关系式为:.
解法二:从图象可以看出:父子俩从出发到相遇花费了15分钟. 设父子俩相遇时,小明走过的路程为x米.
依题意得:,解得x=900,
所以点B的坐标为(15,900),以下同解法一.
(2)解法一:小明取票后,赶往体育馆的时间为:
小明取票花费的时间为:15+5=20分钟.
∵20<25 ∴小明能在比赛开始前到达体育馆.
解法二:在中,令S=0,得. 解得:t=20.
即小明的父亲从出发到体育馆花费的时间为20分钟,因而小明取票的时间也为20分钟.
∵20<25,∴小明能在比赛开始前到达体育馆.
【点评】在数与代数的的问题中常通过建立方程、函数等不同数学模型解决问题,解题策略不同,要注意优化解题方案和过程。
类型三、综合探索型问题
例题7.(2010山东青岛)已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC = 8 cm,BC = 6 cm,EF = 9 cm.
如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由.
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.(图(3)供同学们做题使用)
解答:(1)∵点A在线段PQ的垂直平分线上,
∴AP = AQ.
∵∠DEF = 45°,∠ACB = 90°,∠DEF+∠ACB+∠EQC = 180°,
∴∠EQC = 45°.
∴∠DEF =∠EQC.
∴CE = CQ.
由题意知:CE = t,BP =2 t,
∴CQ = t.
∴AQ = 8-t.
在Rt△ABC中,由勾股定理得:AB = 10 cm .
则AP = 10-2 t.
∴10-2 t = 8-t.
解得:t = 2.
答:当t = 2 s时,点A在线段PQ的垂直平分线上.
(2)过P作,交BE于M,
∴.
在Rt△ABC和Rt△BPM中,,
∴ . ∴PM = .
∵BC = 6 cm,CE = t, ∴ BE = 6-t.
∴y = S△ABC-S△BPE =-= -
= = .
∵,∴抛物线开口向上.
∴当t = 3时,y最小=.
答:当t = 3s时,四边形APEC的面积最小,最小面积为cm2.
(3)假设存在某一时刻t,使点P、Q、F三点在同一条直线上.
过P作,交AC于N,
∴.
∵,∴△PAN ∽△BAC.
∴.
∴.
∴,.
∵NQ = AQ-AN,
∴NQ = 8-t-() = .
∵∠ACB = 90°,B、C(E)、F在同一条直线上,
∴∠QCF = 90°,∠QCF = ∠PNQ.
∵∠FQC = ∠PQN,
∴△QCF∽△QNP .
∴ . ∴ .
∵ ∴
解得:t = 1.
答:当t = 1s,点P、Q、F三点在同一条直线上.
例题8.(2010 浙江衢州)△ABC中,∠A=∠B=30°,AB=.把△ABC放在平面直角坐标系中,使AB的中点位于坐标原点O(如图),△ABC可以绕点O作任意角度的旋转.
(1) 当点B在第一象限,纵坐标是时,求点B的横坐标;
(2) 如果抛物线(a≠0)的对称轴经过点C,请你探究:
① 当,,时,A,B两点是否都在这条抛物线上?并说明理由;
② 设b=-2am,是否存在这样的m的值,使A,B两点不可能同时在这条抛物线上?若存在,直接写出m的值;若不存在,请说明理由.
解答:(1) ∵ 点O是AB的中点, ∴ .
设点B的横坐标是x(x>0),则,
解得 ,(舍去).
∴ 点B的横坐标是.
① 当,,时,得
.
以下分两种情况讨论.
情况1:设点C在第一象限(如图甲),则点C的横坐标为,
.
由此,可求得点C的坐标为(,),
点A的坐标为(,),
∵ A,B两点关于原点对称,
∴ 点B的坐标为(,).
将点A的横坐标代入(*)式右边,计算得,即等于点A的纵坐标;
将点B的横坐标代入(*)式右边,计算得,即等于点B的纵坐标.
∴ 在这种情况下,A,B两点都在抛物线上.
情况2:设点C在第四象限(如图乙),则点C的坐标为(,-),
点A的坐标为(,),点B的坐标为( ( http: / / www. / ),).
经计算,A,B两点都不在这条抛物线上.
(情况2另解:经判断,如果A,B两点都在这条抛物线上,那么抛物线将开口向下,而已知的抛物线开口向上.所以A,B两点不可能都在这条抛物线上)
② 存在.m的值是1或-1.(,因为这条抛物线的对称轴经过点C,所以-1≤m≤1.当m=±1时,点C在x轴上,此时A,B两点都在y轴上.因此当m=±1时,A,B两点不可能同时在这条抛物线上)
【技巧提炼】
因探索型问题一般没有明确的结论,没有固定的形式和方法,需要自己通过观察、分析、比较、概括、推理、判断等探索活动来确定所需求的结论或条件或方法,因而解题的策略是将其转化为封闭性问题.
探索条件的开放题的解题策略是:分析时,把问题的结论作为条件(假设问题的结论成立),借此探索相关的关系;解答时,把探索的关系作为条件,证明此时结论成立。务必要注意这类问题的书写形式。不能把结论当着条件来使用,只能以探索的条件作为条件说明此时结论的正确性。
探索结论的开放题的解题策略是:直接从已知条件入手,通过推理或猜想得出结论。在探索过程中可从特殊情景入手,通过观察、分析、归纳、判断来作一番猜测,再就一般情形去认证结论。这里的关键是抓住命题的条件及特点归纳总结出一般结论。特别要注意题目的具体要求,有些问题只要求探索到满足条件的某种情况,只要给出答案就可以,有些问题要探索出满足条件的所有可能情况,这时就必须考虑全面。也有些问题要求给出全部的答案,但不要求每种情况都给出严谨的证明或完整的探讨过程,解答时务必要看清题目具体的要求,正确的解答。
【体验中考】
1.(2010江苏盐城)写出图象经过点(1,-1)的一个函数关系式 .
2.(2010湖北随州)已知抛物线顶点为C(1,1)且过原点O.过抛物线上一点P(x,y)向直线作垂线,垂足为M,连FM(如图).
(1)求字母a,b,c的值;
(2)在直线x=1上有一点,求以PM为底边的等腰三角形PFM的P点的坐标,并证明此时△PFM为正三角形;
(3)对抛物线上任意一点P,是否总存在一点N(1,t),使PM=PN恒成立,若存在请求出t值,若不存在请说明理由.
3.(2010辽宁丹东)如图,平面直角坐标系中有一直角梯形OMNH,点H的坐标为(-8,0),点N的坐标为(-6,-4).
(1)画出直角梯形OMNH绕点O旋转180°的图形OABC,并写出顶点A,B,C的坐标(点M的对应点为A, 点N的对应点为B, 点H的对应点为C);
(2)求出过A,B,C三点的抛物线的表达式;
(3)截取CE=OF=AG=m,且E,F,G分别在线段CO,OA,AB上,求四边形BEFG的面积S与m之间的函数关系式,并写出自变量m的取值范围;面积S是否存在最小值 若存在,请求出这个最小值;若不存在,请说明理由;
(4)在(3)的情况下,四边形BEFG是否存在邻边相等的情况,若存在,请直接写出此时m的值,并指出相等的邻边;若不存在,说明理由.
4.(2010山东临沂)如图1,已知矩形,点是边的中点,且.
(1)判断的形状,并说明理由;
(2)保持图1中的固定不变,绕点旋转所在的直线到图2中的位置(当垂线段、在直线的同侧).试探究线段、、长度之间有什么关系?并给予证明;
(3)保持图2 中的固定不变,继续绕点旋转所在的直线到图3中的位置(当垂线段、在直线的异侧).试探究线段、、长度之间有什么关系?并给予证明.
5.(2010江苏宿迁)已知抛物线交x轴于A(1,0)、B(3,0)两点,交y轴于点C,其顶点为D.
(1)求b、c的值并写出抛物线的对称轴;
(2)连接BC,过点O作直线OE⊥BC交抛物线
的对称轴于点E.求证:四边形ODBE是等腰梯形;
(3)抛物线上是否存在点Q,使得△OBQ的面积
等于四边形ODBE的面积的?若存在,求点Q的坐标;
若不存在,请说明理由.
6.(2010安徽蚌埠)如图1、2是两个相似比为:的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合。
⑴ 在图3中,绕点旋转小直角三角形,使两直角边分别与交于点,如图4。求证:;
⑵ 若在图3中,绕点旋转小直角三角形,使它的斜边和延长线分别与交于点,如图5,此时结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由。
⑶ 如图,在正方形中,分别是边上的点,满足的周长等于正方形的周长的一半,分别与对角线交于,试问线段、、能否构成三角形的三边长?若能,指出三角形的形状,并给出证明;若不能,请说明理由。
7.(2010福建泉州))我们容易发现:反比例函数的图象是一个中心对称图形.你可以利用这一结论解决问题.如图,在同一直角坐标系中,正比例函数的图象可以看作是:将轴所在的直线绕着原点逆时针旋转α度角后的图形.若它与反比例函数的图象分别交于第一、三象限的点、,已知点、.
(1)直接判断并填写:不论α取何值,四边形的形状一定是 ;
(2)①当点为时,四边形是矩形,试求、α、和有值;
②观察猜想:对①中的值,能使四边形为矩形的点共有几个?
(3)试探究:四边形能不能是菱形?若能, 直接写出B点的坐标, 若不能, 说明理由.
8.(2010福建南平)如图1,在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作□APCD,AC与PD相交于点E,已知∠ABC=∠AEP=α(0°<α<90°).
(1)求证:∠EAP=∠EPA;
(2)□APCD是否为矩形?请说明理由;
(3)如图2,F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系,并证明你的结论.
9.(2010江苏无锡)
(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°—∠AMN —∠AMB=180°—∠B—∠AMB=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正边形ABCD……X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
10.是等边三角形,点D是射线BC上的一个动点(点D不与点B、C重合),是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.如图(a)所示,当点D在线段BC上时.
(1)求证:;
(2)探究四边形是怎样特殊的四边形?并说明理由;
答案:
1.【答案】y=-x或y=-或y=x2-2x,答案不唯一
2.【答案】(1)a=-1,b=2,c=0
(2)过P作直线x=1的垂线,可求P的纵坐标为,横坐标为.此时,MP=MF=PF=1,故△MPF为正三角形.
(3)不存在.因为当t<,x<1时,PM与PN不可能相等,同理,当t>,x>1时,PM与PN不可能相等.
3.【答案】(1) 利用中心对称性质,画出梯形OABC.
∵A,B,C三点与M,N,H分别关于点O中心对称,
∴A(0,4),B(6,4),C(8,0)
(2)设过A,B,C三点的抛物线关系式为,
∵抛物线过点A(0,4),
∴.则抛物线关系式为.
将B(6,4), C(8,0)两点坐标代入关系式,得
解得
所求抛物线关系式为:.
(3)∵OA=4,OC=8,∴AF=4-m,OE=8-m.
∴
OA(AB+OC)AF·AGOE·OFCE·OA
( 0<<4)
∵. ∴当时,S的取最小值.
又∵0<m<4,∴不存在m值,使S的取得最小值.
(4)当时,GB=GF,当时,BE=BG.
4.【答案】(1)△ABC是等腰直角三角形。
如图(1)在矩形ABED中,
因为点C是边DE的中点,且AB=2AD,
所以AD=DC=CE=EB,
∠D=∠E=90°.
∴Rt△ADC≌Rt△BEC.
∴AC=BC, ∠1=∠2=45°.
∴∠ACB=90°.
∴△ABC是等腰直角三角形。
(2)DE=AD+BE.
如图(2),在Rt△ADC和Rt△BEC中,
∵∠1=∠CAD=90°, ∠1+∠2=90°.
∴∠CAD=∠2.
又∵AC=BC, ∠ADC=∠CEB=90°,
∴Rt△ADC≌Rt△CEB.
∴DC=BE,CE=AD.
∴DC+CE= BE+AD,
即DE=AD+BE.
(3)DE=BE-AD.
如图(3),在Rt△ADC和Rt△CEB中,∵∠1+∠CAD=90°, ∠1+∠2=90°,
∴∠CAD=∠2.
又∵∠ADC=∠CBE=90°,AC=CB, ∴Rt△ADC≌Rt△CBE.
∴DC=BE,CE=AD.∴DC-CE=BE-AD, 即DE=BE-AD.
5.【答案】(1)求出:,,抛物线的对称轴为:x=2
(2) 抛物线的解析式为,易得C点坐标为(0,3),D点坐标为(2,-1)
设抛物线的对称轴DE交x轴于点F,易得F点坐标为(2,0),连接OD,DB,BE
∵OBC是等腰直角三角形,DFB也是等腰直角三角形,E点坐标为(2,2),
∴∠BOE= ∠OBD= ∴OE∥BD
∴四边形ODBE是梯形
在和中,
OD= ,BE=
∴OD= BE
∴四边形ODBE是等腰梯形
(3) 存在,
由题意得:
设点Q坐标为(x,y),
由题意得:
=
∴
当y=1时,即,
∴ , ,
∴Q点坐标为(2+,1)或(2-,1)
当y=-1时,即, ∴x=2,
∴Q点坐标为(2,-1)
综上所述,抛物线上存在三点
Q(2+,1),Q (2-,1) ,Q(2,-1)
使得=.
6.【答案】⑴ 在图4中,由于,将绕点旋转,得,
、。连接
在中有
又垂直平分
代换得
在图5中,由,将绕点旋转,得
连接
在中有
又可证≌,得V
代换得
(3)将绕点瞬时针旋转,得,且
因为的周长等于正方形周长的一半,所以
化简得从而可得≌,
推出
此时该问题就转化为图5中的问题了。由前面的结论知:
,再由勾股定理的逆定理知:
线段、、可构成直角三角形。
7.【答案】(1)平行四边形
(2)①∵点在的图象上,
∴
∴
过作,则
在中,
α=30°
∴
又∵点B、D是正比例函数与反比例函数图象的交点,
∴点B、D关于原点O成中心对称
∴OB=OD=
∵四边形为矩形,且
∴
∴;
②能使四边形为矩形的点B共有2个;
(3)四边形不能是菱形.
法一:∵点、的坐标分别为、
∴四边形的对角线在轴上.
又∵点、分别是正比例函数与反比例函数在第一、三象限的交点.
∴对角线与不可能垂直.
∴四边形不能是菱形
法二:若四边形ABCD为菱形,则对角线AC⊥BD,且AC与BD互相平分,
因为点A、C的坐标分别为(-m,0)、(m,0)
所以点A、C关于原点O对称,且AC在x轴上.
所以BD应在y轴上,这与“点B、D分别在第一、三象限”矛盾,
所以四边形ABCD不可能为菱形.
8.【答案】(1)证明:在ΔABC和ΔAEP中
∵∠ABC=∠AEP,∠BAC=∠EAP
∴ ∠ACB=∠APE
在ΔABC中,AB=BC
∴∠ACB=∠BAC
∴ ∠EPA=∠EAP
答:□ APCD是矩形
∵四边形APCD是平行四边形
∴ AC=2EA, PD=2EP
∵ 由(1)知 ∠EPA=∠EAP
∴ EA=EP
则 AC=PD
∴□APCD是矩形
答: EM=EN
∵EA=EP ∴ ∠EPA=90°- α
∴∠EAM=180°-∠EPA=180°-(90°- α)=90°+ α
由(2)知∠CPB=90°,F是BC的中点,∴ FP=FB
∴∠FPB=∠ABC=α
∴ ∠EPN=∠EPA+∠APN=∠EPA+∠FPB=90°- α+α=90°+α
∴ ∠EAM=∠EPN
∵ ∠AEP绕点E顺时针旋转适当的角度,得到∠MEN
∴ ∠AEP=∠MEN
∴∠AEP- ∠AEN=∠MEN-∠AEN 即 ∠MEA=∠NEP
∴ ΔEAM≌ΔEPN ∴ EM=EN
9.【答案】(1)∵AE=MC,∴BE=BM, ∴∠BEM=∠EMB=45°, ∴∠AEM=135°,
∵CN平分∠DCP,∴∠PCN=45°,∴∠AEM=∠MCN=135°
在△AEM和△MCN中:∵∴△AEM≌△MCN,∴AM=MN
(2)仍然成立.
在边AB上截取AE=MC,连接ME
∵△ABC是等边三角形,
∴AB=BC,∠B=∠ACB=60°,
∴∠ACP=120°.
∵AE=MC,∴BE=BM
∴∠BEM=∠EMB=60°
∴∠AEM=120°.
∵CN平分∠ACP,∴∠PCN=60°,
∴∠AEM=∠MCN=120°
∵∠CMN=180°—∠AMN—∠AMB=180°—∠B—∠AMB=∠BAM
∴△AEM≌△MCN,∴AM=MN
(3)
10.【答案】分析:观察图形,先猜想四边形是平行四边形,已知BC∥EG,从边的路径考虑,既可以再证BC=EG,也可以再证BE∥CG。
(1)证明:
∵和都是等边三角形,
∴.
又∵,
,
∴,
∴.
(2)方法一:由(1)得,
∴.
又∵,∴,
∴.
又∵,∴四边形是平行四边形.
方法二:证出,
得.
由(1)得.得.
∴四边形是平行四边形.
点评:在平行四边形的性质与判定中,在策略上要注意从边、角、对角线中寻找恰当的突破口。矩形、菱形、正方形从平行四边形特殊而来,在判定方法的选择上要注意路径,既可以直接从四边形证得为矩形(菱形),也可以先证明它是平行四边形,再证其为矩形(菱形)。
E
A D
B C
N
M
F
E
A D
B C
N
M
y
H
A
D
O
O
C
P
F
y
G
D
E
x
B
S(米)
t(分)
B
O
O
3 600
15
A
A
D
B
C
F
(
E
)
图(1)
A
D
B
C
F
E
图(2)
P
Q
A
B
C
图(3)
图(2)
Q
A
D
B
C
F
E
P
M
C
E
A
D
B
F
图(3)
P
Q
N
O
y
x
C
B
A
1
1
-1
-1
O
y
x
C
B
A
(甲)
1
1
-1
-1
O
y
x
C
B
A
(乙)
1
1
-1
-1
图1
A
B
D
C
E
P
图2
A
B
D
C
E
P
M
N
F
图1
图2
A
G
C
D
B
F
E
图(a)
O
M
N
H
A
C
E
F
D
B
↑
→
-8
(-6,-4)
x
y
E
F
Q1
Q3
Q2
N
F
M
E
B
D
A
C
N
F
M
E
B
D
A
C
G
【备考点睛】
探索型问题是指那些条件不完备、结论不明确、或答案不唯一、给学生留有较大探索余地的试题。从最近几年来中考中探索性问题逐年攀升的趋势,可预测探索性问题仍将是中考命题“孜孜以求的目标”。
探索型问题一般有两类:
(1)探索条件的开放题;(2)探索结论的开放题。
探索型问题的特点:
(1)题设开放型探索性问题的特点是给出结论,不给出条件或条件残缺,需在给定结论的前提下,探索结论成立的条件,但满足结论成立的条件往往不唯一,答案与已知条件对整个问题而言只要是充分的、相容的、独立的,就视为正确的;
(2)结论开放型探索性问题的特点是给出一定的条件而未给出结论,要求在给定的前提条件下,探索结论的多样性,然后通过推理证明确定结论;
【经典例题】
类型一 条件开放型问题
例题1.(2010福建宁德)如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.
⑴ 求证:△AMB≌△ENB;
⑵ ①当M点在何处时,AM+CM的值最小;
②当M点在何处时,AM+BM+CM的值最小,并说明理由;
⑶ 当AM+BM+CM的最小值为时,求正方形的边长.
解答:⑴∵△ABE是等边三角形,
∴BA=BE,∠ABE=60°.
∵∠MBN=60°,
∴∠MBN-∠ABN=∠ABE-∠ABN.
即∠BMA=∠NBE.
又∵MB=NB,
∴△AMB≌△ENB(SAS).
⑵①当M点落在BD的中点时,AM+CM的值最小.
②如图,连接CE,当M点位于BD与CE的交点处时,
AM+BM+CM的值最小.
理由如下:连接MN.由⑴知,△AMB≌△ENB,
∴AM=EN.
∵∠MBN=60°,MB=NB,
∴△BMN是等边三角形.
∴BM=MN.
∴AM+BM+CM=EN+MN+CM.
根据“两点之间线段最短”,得EN+MN+CM=EC最短
∴当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长.
⑶过E点作EF⊥BC交CB的延长线于F,
∴∠EBF=90°-60°=30°.
设正方形的边长为x,则BF=x,EF=.
在Rt△EFC中,
∵EF2+FC2=EC2,
∴()2+(x+x)2=.
解得,x=(舍去负值).
∴正方形的边长为.
例题2.如图,四边形ABCD是平行四边形.O是对角线AC的中点,过点O的直线EF分别交AB、DC于点E、F,与CB、AD的延长线分别交于点G、H.
(1)写出图中不全等的两个相似三角形(不要求证明);
(2)除AB=CD,AD=BC,OA=OC这三对相等的线段外,图中还有多对相等的线段,请选出其中一对加以证明.
解答:分析:考察了相似的两种基本图形,平行四边形中利用全等三角形的简单证明.
(1) AEH与DFH.(或AEH与BEG, 或BEG与CFG ,或DFH与CFG)
(2)OE=OF.
证明:四边形ABCD是平行四边形,
∥CD, ,
, △△,
.
例题3.(2010 甘肃)如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标;
(2)以B、C、D为顶点的三角形是直角三角形吗?为什么?
(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,请指出符合条件的点P的位置,并直接写出点P的坐标;若不存在,请说明理由.
解答:(1)设该抛物线的解析式为,
由抛物线与y轴交于点C(0,-3),可知.
即抛物线的解析式为.
把A(-1,0)、B(3,0)代入, 得
解得.
∴ 抛物线的解析式为y = x2-2x-3.
∴ 顶点D的坐标为.
(2)以B、C、D为顶点的三角形是直角三角形.
理由如下:
过点D分别作轴、轴的垂线,垂足分别为E、F.
在Rt△BOC中,OB=3,OC=3,∴ .
在Rt△CDF中,DF=1,CF=OF-OC=4-3=1,∴ .
在Rt△BDE中,DE=4,BE=OB-OE=3-1=2,∴ .
∴ , 故△BCD为直角三角形.
(3)连接AC,可知Rt△COA∽ Rt△BCD,
得符合条件的点为O(0,0).
过A作AP1⊥AC交y轴正半轴于P1,
可知Rt△CAP1 ∽ Rt△COA∽ Rt△BCD,
求得符合条件的点为.
过C作CP2⊥AC交x轴正半轴于P2,
可知Rt△P2CA∽ Rt△COA∽ Rt△BCD,
求得符合条件的点为P2(9,0).
∴符合条件的点有三个:
O(0,0),,P2(9,0).
类型二 结论开放型问题
例题4.(2010四川眉山)如图,Rt△AB C 是由Rt△ABC绕点A顺时针旋转得到的,连结CC 交斜边于点E,CC 的延长线交BB 于点F.
(1)证明:△ACE∽△FBE;
(2)设∠ABC=,∠CAC =,试探索
、满足什么关系时,△ACE与△FBE
是全等三角形,并说明理由.
解答:(1)证明:∵Rt△AB C 是由Rt△ABC绕
点A顺时针旋转得到的,
∴AC=AC ,AB=AB ,∠CAB=∠C AB
∴∠CAC =∠BAB
∴∠ACC =∠ABB
又∠AEC=∠FEB
∴△ACE∽△FBE
(2)解:当时,△ACE≌△FBE.
在△ACC中,∵AC=AC ,
∴
在Rt△ABC中,
∠ACC+∠BCE=90°,即,
∴∠BCE=.
∵∠ABC=,
∴∠ABC=∠BCE
∴CE=BE
由(1)知:△ACE∽△FBE,
∴△ACE≌△FBE.
例题5.(2010安徽蚌埠)已知⊙过点(3,4),点与点关于轴对称,过作⊙的切线交轴于点。
⑴ 求的值;
⑵ 如图,设⊙与轴正半轴交点为,点、是线段上的动点(与点不重合),连接并延长、交⊙于点、,直线交轴于点,若是以为底的等腰三角形,试探索的大小怎样变化,请说明理由。
解答:⑴
(2)试探索的大小怎样变化,请说明理由.
解:当、两点在上运动时(与点不重合),的值不变
过点作于,并延长交于,连接,
交于。
因为为等腰三角形, ,
所以平分
所以弧BN=弧CN,所以,
所以
所以=
即当、两点在上运动时(与点不重合),的值不变。
例题6.某天,小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.下图中线段AB、OB分别表示父、子俩送票、取票过程中,离体育馆的路程S(米)与所用时间(分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
(1)求点B的坐标和AB所在直线的函数关系式;
(2)小明能否在比赛开始前到达体育馆?
解答: 从函数图象中“读图找点”,由点的坐标找数量,利用列算式或方程求解,也可以“见形想式”,通过建立函数关系式,利用函数求解。
【解答】(1)解法一:从图象可以看出:父子俩从出发到相遇时花费了15分钟 设小明步行的速度为x米/分,则小明父亲骑车的速度为3x米/分
依题意得:15x+45x=3600. 解得:x=60.
所以两人相遇处离体育馆的距离为60×15=900米.
所以点B的坐标为(15,900).
设直线AB的函数关系式为S=kt+b(k≠0).
由题意,直线AB经过点A(0,3600)、B(15,900)得:解之,得
∴直线AB的函数关系式为:.
解法二:从图象可以看出:父子俩从出发到相遇花费了15分钟. 设父子俩相遇时,小明走过的路程为x米.
依题意得:,解得x=900,
所以点B的坐标为(15,900),以下同解法一.
(2)解法一:小明取票后,赶往体育馆的时间为:
小明取票花费的时间为:15+5=20分钟.
∵20<25 ∴小明能在比赛开始前到达体育馆.
解法二:在中,令S=0,得. 解得:t=20.
即小明的父亲从出发到体育馆花费的时间为20分钟,因而小明取票的时间也为20分钟.
∵20<25,∴小明能在比赛开始前到达体育馆.
【点评】在数与代数的的问题中常通过建立方程、函数等不同数学模型解决问题,解题策略不同,要注意优化解题方案和过程。
类型三、综合探索型问题
例题7.(2010山东青岛)已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC = 8 cm,BC = 6 cm,EF = 9 cm.
如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由.
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.(图(3)供同学们做题使用)
解答:(1)∵点A在线段PQ的垂直平分线上,
∴AP = AQ.
∵∠DEF = 45°,∠ACB = 90°,∠DEF+∠ACB+∠EQC = 180°,
∴∠EQC = 45°.
∴∠DEF =∠EQC.
∴CE = CQ.
由题意知:CE = t,BP =2 t,
∴CQ = t.
∴AQ = 8-t.
在Rt△ABC中,由勾股定理得:AB = 10 cm .
则AP = 10-2 t.
∴10-2 t = 8-t.
解得:t = 2.
答:当t = 2 s时,点A在线段PQ的垂直平分线上.
(2)过P作,交BE于M,
∴.
在Rt△ABC和Rt△BPM中,,
∴ . ∴PM = .
∵BC = 6 cm,CE = t, ∴ BE = 6-t.
∴y = S△ABC-S△BPE =-= -
= = .
∵,∴抛物线开口向上.
∴当t = 3时,y最小=.
答:当t = 3s时,四边形APEC的面积最小,最小面积为cm2.
(3)假设存在某一时刻t,使点P、Q、F三点在同一条直线上.
过P作,交AC于N,
∴.
∵,∴△PAN ∽△BAC.
∴.
∴.
∴,.
∵NQ = AQ-AN,
∴NQ = 8-t-() = .
∵∠ACB = 90°,B、C(E)、F在同一条直线上,
∴∠QCF = 90°,∠QCF = ∠PNQ.
∵∠FQC = ∠PQN,
∴△QCF∽△QNP .
∴ . ∴ .
∵ ∴
解得:t = 1.
答:当t = 1s,点P、Q、F三点在同一条直线上.
例题8.(2010 浙江衢州)△ABC中,∠A=∠B=30°,AB=.把△ABC放在平面直角坐标系中,使AB的中点位于坐标原点O(如图),△ABC可以绕点O作任意角度的旋转.
(1) 当点B在第一象限,纵坐标是时,求点B的横坐标;
(2) 如果抛物线(a≠0)的对称轴经过点C,请你探究:
① 当,,时,A,B两点是否都在这条抛物线上?并说明理由;
② 设b=-2am,是否存在这样的m的值,使A,B两点不可能同时在这条抛物线上?若存在,直接写出m的值;若不存在,请说明理由.
解答:(1) ∵ 点O是AB的中点, ∴ .
设点B的横坐标是x(x>0),则,
解得 ,(舍去).
∴ 点B的横坐标是.
① 当,,时,得
.
以下分两种情况讨论.
情况1:设点C在第一象限(如图甲),则点C的横坐标为,
.
由此,可求得点C的坐标为(,),
点A的坐标为(,),
∵ A,B两点关于原点对称,
∴ 点B的坐标为(,).
将点A的横坐标代入(*)式右边,计算得,即等于点A的纵坐标;
将点B的横坐标代入(*)式右边,计算得,即等于点B的纵坐标.
∴ 在这种情况下,A,B两点都在抛物线上.
情况2:设点C在第四象限(如图乙),则点C的坐标为(,-),
点A的坐标为(,),点B的坐标为( ( http: / / www. / ),).
经计算,A,B两点都不在这条抛物线上.
(情况2另解:经判断,如果A,B两点都在这条抛物线上,那么抛物线将开口向下,而已知的抛物线开口向上.所以A,B两点不可能都在这条抛物线上)
② 存在.m的值是1或-1.(,因为这条抛物线的对称轴经过点C,所以-1≤m≤1.当m=±1时,点C在x轴上,此时A,B两点都在y轴上.因此当m=±1时,A,B两点不可能同时在这条抛物线上)
【技巧提炼】
因探索型问题一般没有明确的结论,没有固定的形式和方法,需要自己通过观察、分析、比较、概括、推理、判断等探索活动来确定所需求的结论或条件或方法,因而解题的策略是将其转化为封闭性问题.
探索条件的开放题的解题策略是:分析时,把问题的结论作为条件(假设问题的结论成立),借此探索相关的关系;解答时,把探索的关系作为条件,证明此时结论成立。务必要注意这类问题的书写形式。不能把结论当着条件来使用,只能以探索的条件作为条件说明此时结论的正确性。
探索结论的开放题的解题策略是:直接从已知条件入手,通过推理或猜想得出结论。在探索过程中可从特殊情景入手,通过观察、分析、归纳、判断来作一番猜测,再就一般情形去认证结论。这里的关键是抓住命题的条件及特点归纳总结出一般结论。特别要注意题目的具体要求,有些问题只要求探索到满足条件的某种情况,只要给出答案就可以,有些问题要探索出满足条件的所有可能情况,这时就必须考虑全面。也有些问题要求给出全部的答案,但不要求每种情况都给出严谨的证明或完整的探讨过程,解答时务必要看清题目具体的要求,正确的解答。
【体验中考】
1.(2010江苏盐城)写出图象经过点(1,-1)的一个函数关系式 .
2.(2010湖北随州)已知抛物线顶点为C(1,1)且过原点O.过抛物线上一点P(x,y)向直线作垂线,垂足为M,连FM(如图).
(1)求字母a,b,c的值;
(2)在直线x=1上有一点,求以PM为底边的等腰三角形PFM的P点的坐标,并证明此时△PFM为正三角形;
(3)对抛物线上任意一点P,是否总存在一点N(1,t),使PM=PN恒成立,若存在请求出t值,若不存在请说明理由.
3.(2010辽宁丹东)如图,平面直角坐标系中有一直角梯形OMNH,点H的坐标为(-8,0),点N的坐标为(-6,-4).
(1)画出直角梯形OMNH绕点O旋转180°的图形OABC,并写出顶点A,B,C的坐标(点M的对应点为A, 点N的对应点为B, 点H的对应点为C);
(2)求出过A,B,C三点的抛物线的表达式;
(3)截取CE=OF=AG=m,且E,F,G分别在线段CO,OA,AB上,求四边形BEFG的面积S与m之间的函数关系式,并写出自变量m的取值范围;面积S是否存在最小值 若存在,请求出这个最小值;若不存在,请说明理由;
(4)在(3)的情况下,四边形BEFG是否存在邻边相等的情况,若存在,请直接写出此时m的值,并指出相等的邻边;若不存在,说明理由.
4.(2010山东临沂)如图1,已知矩形,点是边的中点,且.
(1)判断的形状,并说明理由;
(2)保持图1中的固定不变,绕点旋转所在的直线到图2中的位置(当垂线段、在直线的同侧).试探究线段、、长度之间有什么关系?并给予证明;
(3)保持图2 中的固定不变,继续绕点旋转所在的直线到图3中的位置(当垂线段、在直线的异侧).试探究线段、、长度之间有什么关系?并给予证明.
5.(2010江苏宿迁)已知抛物线交x轴于A(1,0)、B(3,0)两点,交y轴于点C,其顶点为D.
(1)求b、c的值并写出抛物线的对称轴;
(2)连接BC,过点O作直线OE⊥BC交抛物线
的对称轴于点E.求证:四边形ODBE是等腰梯形;
(3)抛物线上是否存在点Q,使得△OBQ的面积
等于四边形ODBE的面积的?若存在,求点Q的坐标;
若不存在,请说明理由.
6.(2010安徽蚌埠)如图1、2是两个相似比为:的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合。
⑴ 在图3中,绕点旋转小直角三角形,使两直角边分别与交于点,如图4。求证:;
⑵ 若在图3中,绕点旋转小直角三角形,使它的斜边和延长线分别与交于点,如图5,此时结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由。
⑶ 如图,在正方形中,分别是边上的点,满足的周长等于正方形的周长的一半,分别与对角线交于,试问线段、、能否构成三角形的三边长?若能,指出三角形的形状,并给出证明;若不能,请说明理由。
7.(2010福建泉州))我们容易发现:反比例函数的图象是一个中心对称图形.你可以利用这一结论解决问题.如图,在同一直角坐标系中,正比例函数的图象可以看作是:将轴所在的直线绕着原点逆时针旋转α度角后的图形.若它与反比例函数的图象分别交于第一、三象限的点、,已知点、.
(1)直接判断并填写:不论α取何值,四边形的形状一定是 ;
(2)①当点为时,四边形是矩形,试求、α、和有值;
②观察猜想:对①中的值,能使四边形为矩形的点共有几个?
(3)试探究:四边形能不能是菱形?若能, 直接写出B点的坐标, 若不能, 说明理由.
8.(2010福建南平)如图1,在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作□APCD,AC与PD相交于点E,已知∠ABC=∠AEP=α(0°<α<90°).
(1)求证:∠EAP=∠EPA;
(2)□APCD是否为矩形?请说明理由;
(3)如图2,F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系,并证明你的结论.
9.(2010江苏无锡)
(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°—∠AMN —∠AMB=180°—∠B—∠AMB=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正边形ABCD……X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
10.是等边三角形,点D是射线BC上的一个动点(点D不与点B、C重合),是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.如图(a)所示,当点D在线段BC上时.
(1)求证:;
(2)探究四边形是怎样特殊的四边形?并说明理由;
答案:
1.【答案】y=-x或y=-或y=x2-2x,答案不唯一
2.【答案】(1)a=-1,b=2,c=0
(2)过P作直线x=1的垂线,可求P的纵坐标为,横坐标为.此时,MP=MF=PF=1,故△MPF为正三角形.
(3)不存在.因为当t<,x<1时,PM与PN不可能相等,同理,当t>,x>1时,PM与PN不可能相等.
3.【答案】(1) 利用中心对称性质,画出梯形OABC.
∵A,B,C三点与M,N,H分别关于点O中心对称,
∴A(0,4),B(6,4),C(8,0)
(2)设过A,B,C三点的抛物线关系式为,
∵抛物线过点A(0,4),
∴.则抛物线关系式为.
将B(6,4), C(8,0)两点坐标代入关系式,得
解得
所求抛物线关系式为:.
(3)∵OA=4,OC=8,∴AF=4-m,OE=8-m.
∴
OA(AB+OC)AF·AGOE·OFCE·OA
( 0<<4)
∵. ∴当时,S的取最小值.
又∵0<m<4,∴不存在m值,使S的取得最小值.
(4)当时,GB=GF,当时,BE=BG.
4.【答案】(1)△ABC是等腰直角三角形。
如图(1)在矩形ABED中,
因为点C是边DE的中点,且AB=2AD,
所以AD=DC=CE=EB,
∠D=∠E=90°.
∴Rt△ADC≌Rt△BEC.
∴AC=BC, ∠1=∠2=45°.
∴∠ACB=90°.
∴△ABC是等腰直角三角形。
(2)DE=AD+BE.
如图(2),在Rt△ADC和Rt△BEC中,
∵∠1=∠CAD=90°, ∠1+∠2=90°.
∴∠CAD=∠2.
又∵AC=BC, ∠ADC=∠CEB=90°,
∴Rt△ADC≌Rt△CEB.
∴DC=BE,CE=AD.
∴DC+CE= BE+AD,
即DE=AD+BE.
(3)DE=BE-AD.
如图(3),在Rt△ADC和Rt△CEB中,∵∠1+∠CAD=90°, ∠1+∠2=90°,
∴∠CAD=∠2.
又∵∠ADC=∠CBE=90°,AC=CB, ∴Rt△ADC≌Rt△CBE.
∴DC=BE,CE=AD.∴DC-CE=BE-AD, 即DE=BE-AD.
5.【答案】(1)求出:,,抛物线的对称轴为:x=2
(2) 抛物线的解析式为,易得C点坐标为(0,3),D点坐标为(2,-1)
设抛物线的对称轴DE交x轴于点F,易得F点坐标为(2,0),连接OD,DB,BE
∵OBC是等腰直角三角形,DFB也是等腰直角三角形,E点坐标为(2,2),
∴∠BOE= ∠OBD= ∴OE∥BD
∴四边形ODBE是梯形
在和中,
OD= ,BE=
∴OD= BE
∴四边形ODBE是等腰梯形
(3) 存在,
由题意得:
设点Q坐标为(x,y),
由题意得:
=
∴
当y=1时,即,
∴ , ,
∴Q点坐标为(2+,1)或(2-,1)
当y=-1时,即, ∴x=2,
∴Q点坐标为(2,-1)
综上所述,抛物线上存在三点
Q(2+,1),Q (2-,1) ,Q(2,-1)
使得=.
6.【答案】⑴ 在图4中,由于,将绕点旋转,得,
、。连接
在中有
又垂直平分
代换得
在图5中,由,将绕点旋转,得
连接
在中有
又可证≌,得V
代换得
(3)将绕点瞬时针旋转,得,且
因为的周长等于正方形周长的一半,所以
化简得从而可得≌,
推出
此时该问题就转化为图5中的问题了。由前面的结论知:
,再由勾股定理的逆定理知:
线段、、可构成直角三角形。
7.【答案】(1)平行四边形
(2)①∵点在的图象上,
∴
∴
过作,则
在中,
α=30°
∴
又∵点B、D是正比例函数与反比例函数图象的交点,
∴点B、D关于原点O成中心对称
∴OB=OD=
∵四边形为矩形,且
∴
∴;
②能使四边形为矩形的点B共有2个;
(3)四边形不能是菱形.
法一:∵点、的坐标分别为、
∴四边形的对角线在轴上.
又∵点、分别是正比例函数与反比例函数在第一、三象限的交点.
∴对角线与不可能垂直.
∴四边形不能是菱形
法二:若四边形ABCD为菱形,则对角线AC⊥BD,且AC与BD互相平分,
因为点A、C的坐标分别为(-m,0)、(m,0)
所以点A、C关于原点O对称,且AC在x轴上.
所以BD应在y轴上,这与“点B、D分别在第一、三象限”矛盾,
所以四边形ABCD不可能为菱形.
8.【答案】(1)证明:在ΔABC和ΔAEP中
∵∠ABC=∠AEP,∠BAC=∠EAP
∴ ∠ACB=∠APE
在ΔABC中,AB=BC
∴∠ACB=∠BAC
∴ ∠EPA=∠EAP
答:□ APCD是矩形
∵四边形APCD是平行四边形
∴ AC=2EA, PD=2EP
∵ 由(1)知 ∠EPA=∠EAP
∴ EA=EP
则 AC=PD
∴□APCD是矩形
答: EM=EN
∵EA=EP ∴ ∠EPA=90°- α
∴∠EAM=180°-∠EPA=180°-(90°- α)=90°+ α
由(2)知∠CPB=90°,F是BC的中点,∴ FP=FB
∴∠FPB=∠ABC=α
∴ ∠EPN=∠EPA+∠APN=∠EPA+∠FPB=90°- α+α=90°+α
∴ ∠EAM=∠EPN
∵ ∠AEP绕点E顺时针旋转适当的角度,得到∠MEN
∴ ∠AEP=∠MEN
∴∠AEP- ∠AEN=∠MEN-∠AEN 即 ∠MEA=∠NEP
∴ ΔEAM≌ΔEPN ∴ EM=EN
9.【答案】(1)∵AE=MC,∴BE=BM, ∴∠BEM=∠EMB=45°, ∴∠AEM=135°,
∵CN平分∠DCP,∴∠PCN=45°,∴∠AEM=∠MCN=135°
在△AEM和△MCN中:∵∴△AEM≌△MCN,∴AM=MN
(2)仍然成立.
在边AB上截取AE=MC,连接ME
∵△ABC是等边三角形,
∴AB=BC,∠B=∠ACB=60°,
∴∠ACP=120°.
∵AE=MC,∴BE=BM
∴∠BEM=∠EMB=60°
∴∠AEM=120°.
∵CN平分∠ACP,∴∠PCN=60°,
∴∠AEM=∠MCN=120°
∵∠CMN=180°—∠AMN—∠AMB=180°—∠B—∠AMB=∠BAM
∴△AEM≌△MCN,∴AM=MN
(3)
10.【答案】分析:观察图形,先猜想四边形是平行四边形,已知BC∥EG,从边的路径考虑,既可以再证BC=EG,也可以再证BE∥CG。
(1)证明:
∵和都是等边三角形,
∴.
又∵,
,
∴,
∴.
(2)方法一:由(1)得,
∴.
又∵,∴,
∴.
又∵,∴四边形是平行四边形.
方法二:证出,
得.
由(1)得.得.
∴四边形是平行四边形.
点评:在平行四边形的性质与判定中,在策略上要注意从边、角、对角线中寻找恰当的突破口。矩形、菱形、正方形从平行四边形特殊而来,在判定方法的选择上要注意路径,既可以直接从四边形证得为矩形(菱形),也可以先证明它是平行四边形,再证其为矩形(菱形)。
E
A D
B C
N
M
F
E
A D
B C
N
M
y
H
A
D
O
O
C
P
F
y
G
D
E
x
B
S(米)
t(分)
B
O
O
3 600
15
A
A
D
B
C
F
(
E
)
图(1)
A
D
B
C
F
E
图(2)
P
Q
A
B
C
图(3)
图(2)
Q
A
D
B
C
F
E
P
M
C
E
A
D
B
F
图(3)
P
Q
N
O
y
x
C
B
A
1
1
-1
-1
O
y
x
C
B
A
(甲)
1
1
-1
-1
O
y
x
C
B
A
(乙)
1
1
-1
-1
图1
A
B
D
C
E
P
图2
A
B
D
C
E
P
M
N
F
图1
图2
A
G
C
D
B
F
E
图(a)
O
M
N
H
A
C
E
F
D
B
↑
→
-8
(-6,-4)
x
y
E
F
Q1
Q3
Q2
N
F
M
E
B
D
A
C
N
F
M
E
B
D
A
C
G
同课章节目录
