2011中考冲刺数学专题8-新概念型问题
文档属性
| 名称 | 2011中考冲刺数学专题8-新概念型问题 |

|
|
| 格式 | zip | ||
| 文件大小 | 490.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 新人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-20 00:00:00 | ||
图片预览




文档简介
2011中考冲刺数学专题8——新概念型问题
【备考点睛】
新概念型是近几年中考的热点问题,试题的特点在学生已学数学知识的基础上,对旧知识进行重新包装,给出一个“新概念”,然后要求学生学习和运用这个“新概念”来解决相应的数学问题,这类试题对培养学生的阅读理解能力和独立获取新知识、解决新问题的能力有非常重要的作用.面对一个新概念,阅读时至关重要的是用自己的语言来理解它,并把它与熟悉的相关数学知识相挂靠,把一个全新的问题化为熟悉的问题去处理.这类试题能很好地考查学生的数学阅读理解能力、数学抽象概括能力和对“新概念”的实际应用能力。
【经典例题】
例题1。 定义:到凸四边形一组对边距离相等,到另一组对边距离也相等的点叫凸四边形的准内点.如图1,PH=PJ,PI=PG,则点P就是四边形ABCD的准内点.
(1)如图2, 与的角平分线相交于点.求证:点是四边形的准内点.
(2)分别画出图3平行四边形和图4梯形的准内点.(作图工具不限,不写作法,但要有必要的说明)
(3)判断下列命题的真假,在括号内填“真”或“假”.
①任意凸四边形一定存在准内点.( )
②任意凸四边形一定只有一个准内点.( )
③若是任意凸四边形的准内点,则PA+PB=PC+PD或PA+PC=PB+PD.( )
解答:解析:在理解新新概念——准内点的同时,结合已学角的平分线的性质与判定——角平分线上的点到角的两边的距离相等,到角的两边的距离相等的点在这个角的平分线上。当两组对边不平行时,如图1中的点P是直线AD与BC的夹角平分线、直线AB与DC的夹角平分线的交点,当两组对边平行时利用全等三角形等方法构造。
详解:(1)如图2,过点作
,
∵平分, ∴.
同理 .
∴是四边形的准内点.
(2)
平行四边形对角线AC、BD的交点就是准内点,如图3(1).或者取平行四边形两对边中点连线的交点就是准内点,如图3(2);梯形两腰夹角的平分线与梯形中位线的交点就是准内点.如图4.
(3)真;真;假.
例题2。 (2010湖南益阳)我们把对称中心重合,四边分别平行的两个正方形之间的部分叫“方形环”,易知方形环四周的宽度相等.
一条直线l与方形环的边线有四个交点、、、.小明在探究线段与 的数量关系时,从点、向对边作垂线段、,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题:
⑴当直线l与方形环的对边相交时(如图1),直线l分别交、、、于、、、,小明发现与相等,请你帮他说明理由;
⑵当直线l与方形环的邻边相交时(如图2),l分别交、、、于、、、,l与的夹角为,你认为与还相等吗?若相等,说明理由;若不相等,求出的值(用含的三角函数表示).
解答:⑴解: 在方形环中,
∵∥
∴
∴△≌△
∴
⑵解法一:∵
∴∽
∴
∵
∴ (或)
①当时,tan=1,则
②当时,
则 (或)
解法二:在方形环中,
又∵
∴∥
∴
在与中,
HYPERLINK "http://www./"
即 (或)
①当时,
②当时,
则 (或)
例题3。 阅读材料:
如图1-1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法:,即三角形面积等于水平宽与铅垂高乘积的一半.
解答下列问题:
如图1-2,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.
(1)求抛物线和直线AB的解析式;
(2)点P是抛物线(在第一象限内)上的一个动点,连结PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及;
(3)是否存在一点P,使S△PAB=S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
解答:解析:(1)材料中给出了一个基本图形和计算三角形面积的新方法,在解决问题中一定要运用新方法,切不可只用教材中的计算方法,否则问题就很难求解。(2)理解材料是解决问题的关键,在运用公式时注意结合图形理解水平宽与铅垂高的含义,能指出△CAB的铅垂高为CD与水平宽为OA,△PAB的水平宽仍为OA,铅垂高为点P的纵坐标与点B的纵坐标的差。
详解:(1)设抛物线的解析式为:,把A(3,0)代入解析式求得
所以
设直线AB的解析式为:
由求得B点的坐标为
把,代入中
解得:
所以
(2)因为C点坐标为(1,4)
所以当x=1时,y1=4,y2=2
所以CD=4-2=2
(平方单位)
(3)假设存在符合条件的点P,设P点的横坐标为x,△PAB的铅垂高为h,则 HYPERLINK "http:///" 由S△PAB=S△CAB得:
化简得:解得,
将代入中,
解得P点坐标为。
点评:在坐标系中求几何量,注意点的横、纵坐标与线段长度的关联。
例题4。 (2010 浙江台州)类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为 3+()=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为.
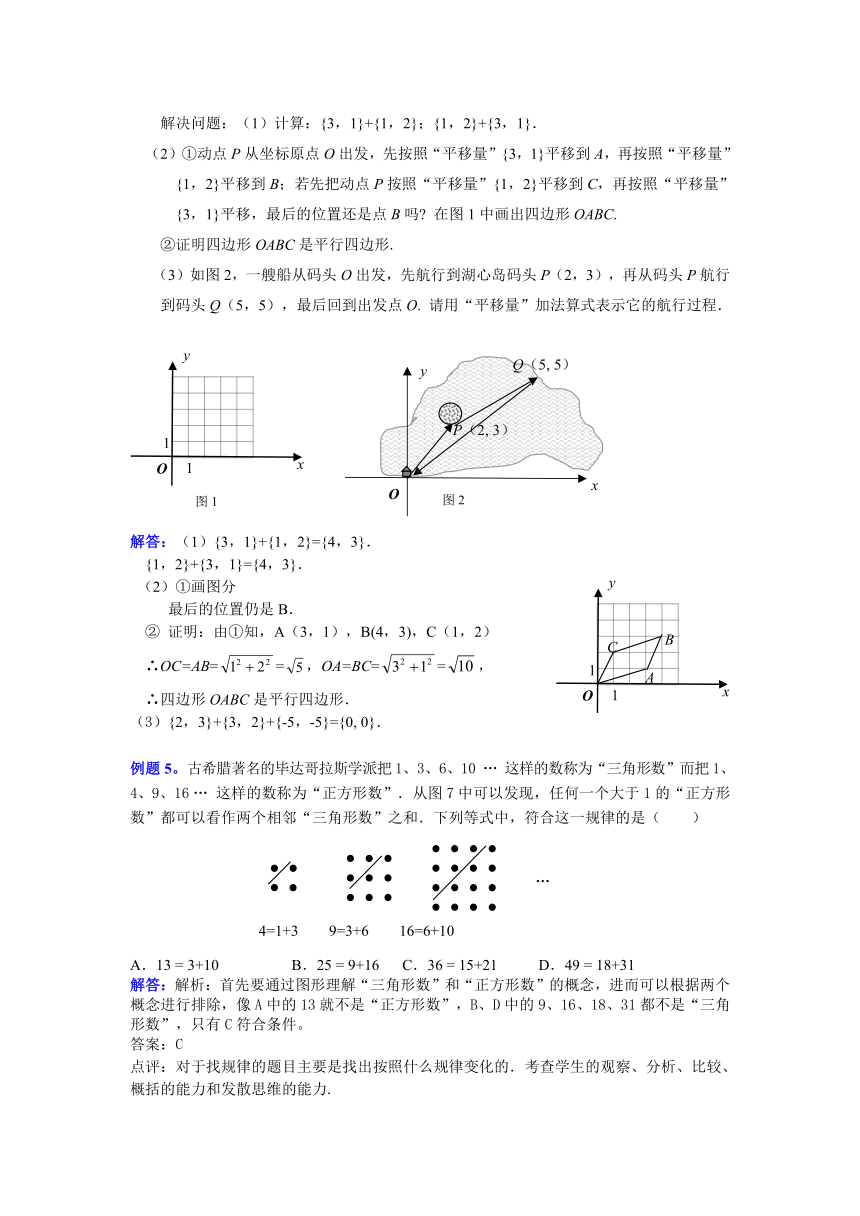
解决问题:(1)计算:{3,1}+{1,2};{1,2}+{3,1}.
(2)①动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”
{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”
{3,1}平移,最后的位置还是点B吗 在图1中画出四边形OABC.
②证明四边形OABC是平行四边形.
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程.
解答:(1){3,1}+{1,2}={4,3}.
{1,2}+{3,1}={4,3}.
(2)①画图分
最后的位置仍是B.
② 证明:由①知,A(3,1),B(4,3),C(1,2)
∴OC=AB==,OA=BC==,
∴四边形OABC是平行四边形.
(3){2,3}+{3,2}+{-5,-5}={0, 0}.
例题5。古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”而把1、4、9、16 … 这样的数称为“正方形数”.从图7中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )
A.13 = 3+10 B.25 = 9+16 C.36 = 15+21 D.49 = 18+31
解答:解析:首先要通过图形理解“三角形数”和“正方形数”的概念,进而可以根据两个概念进行排除,像A中的13就不是“正方形数”,B、D中的9、16、18、31都不是“三角形数”,只有C符合条件。
答案:C
点评:对于找规律的题目主要是找出按照什么规律变化的.考查学生的观察、分析、比较、概括的能力和发散思维的能力.
例题6。(2010浙江绍兴)在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,
叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.
(1)求函数y=x+3的坐标三角形的三条边长;
(2)若函数y=x+b(b为常数)的坐标三角形
周长为16, 求此三角形面积.
解答:(1) ∵ 直线y=x+3与x轴的交点坐标为(4,0),与y轴交点坐标为(0,3),
∴函数y=x+3的坐标三角形的三条边长分别为3,4,5.
(2) 直线y=x+b与x轴的交点坐标为(,0),与y轴交点坐标为(0,b),
当b>0时,,得b =4,此时,坐标三角形面积为;
当b<0时,,得b =-4,此时,坐标三角形面积为.
综上,当函数y=x+b的坐标三角形周长为16时,面积为.
例题7。对于任意的两个实数对和,规定:当时,有;运算“”为:;运算“”为:.设、都是实数,若,则
解答:因为,所以p=2,2q=-4,
所以p=2,q=-2.所以(1+p,2+q)=
【技巧提炼】
解决新概念型问题的关键是把握“新概念”的实质,正确理解“新概念”的内涵。首先仔细阅读对于“新概念”的定义;然后运用“新概念”的知识解决新问题.因此,要掌握好初中数学的基础知识,更要注重提高阅读理解、知识迁移、分析转化、探索归纳等多方面的素质,其实,解决问题的思想方法还是通常学到的方法,所以,只要认真思考,还是可以解决的。
【体验中考】
1.(2010安徽蚌埠)若表示不超过的最大整数(如等),则
_________________。
2.(2010广西南宁)古希腊数学家把数叫做三角数,它有一定的规律性.若把一个三角形数记为,第二个三角形数记为,第个三角形数记为,计算, ,由此推算, , .
3.(2010湖南常德)如图,一个数表有7行7列,设表示第i行第j列上的数(其中i=1,2,3,…,7,j=1,2,3,…,7). 例如:第5行第3列上的数.
则(1)= ;
(2)此数表中的四个数满足= .
4.(2010 重庆江津)我们定义,例如=2×5-3×4=10-12=-2.若、均为整数,且满足1<<3,则的值是_________.
5.(2010四川达州)在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换:
①,如;② ,如.
按照以上变换有:,那么等于
A.(3,2) B.(3,-2)
C.(-3,2) D.(-3,-2)
6.(2010浙江宁波)《几何原本》的诞生,标志着几何学已成为一个有着严密理论系统和科学方法的学科,它 奠定了现代数学的基础. 它是下列哪位数学家的著作
(A)欧几里得 (B)杨辉 (C)笛卡尔 (D)刘徽
7.(2010安徽蚌埠)记=,令,称为,,……,这列数的“理想数”。已知,,……,的“理想数”为2004,那么8,,,……,的“理想数”为
A.2004 B.2006 C.2008 D.2010
8.(2010鄂尔多斯)定义新运算: a b=,则函数y=3 x的图象大致是
9.(2010浙江杭州)定义[]为函数的特征数, 下面给出特征数为 [2m,1 – m , –1– m] 的函数的一些结论:
① 当m = – 3时,函数图象的顶点坐标是(,);
② 当m > 0时,函数图象截x轴所得的线段长度大于;
③ 当m < 0时,函数在x >时,y随x的增大而减小;
④ 当m 0时,函数图象经过同一个点.
其中正确的结论有
A. ①②③④ B. ①②④ C. ①③④ D. ②④
10.(2010 山东东营)把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换.在自然界和日常生活中,大量地存在这种图形变换(如图甲).结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,两个对应三角形(如图乙)的对应点所具有的性质是( )
(A)对应点连线与对称轴垂直 (B)对应点连线被对称轴平分
(C)对应点连线被对称轴垂直平分 (D)对应点连线互相平行
11.阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数的图象为直线,一次函数的图象为直线,若,且,我们就称直线与直线互相平行. 解答下面的问题:
(1)求过点且与已知直线平行的直线的函数表达式,并画出直线 的图象;
(2)设直线分别与轴、轴交于点、,如果直线:与直线平行且交轴于点,求出△的面积关于的函数表达式.
12.(2010 江苏连云港) 如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.如,平行四边形的一条对线所在的直线就是平行四边形的一条面积等分线.
(1)三角形的中线、高线、角平分线分别所在的直线一定是三角形的面积等分线的有________;
(2)如图1,梯形ABCD中,AB∥DC,如果延长DC到E,使CE=AB,连接AE,那么有S梯形ABCD=S△ABE.请你给出这个结论成立的理由,并过点A作出梯形ABCD的面积等分线(不写作法,保留作图痕迹);
(3)如图,四边形ABCD中,AB与CD不平行,S△ADC>S△ABC,过点A能否作出四边形ABCD的面积等分线?若能,请画出面积等分线,并给出证明;若不能,说明理由.
13.如图,四边形ABCD中,AB=AD,CB=CD,但AD CD,我们称这样的四边形为“半菱形”。小明说“‘半菱形’的面积等于两条对角线乘积的一半”。他的说法正确吗?请你判断并证明你的结论。
14.(2010安徽蚌埠)定义:在平面内,我们把既有大小又有方向的量叫做平面向量。平面向量可以用有向线段表示,有向线段的长度表示向量的大小,有向线段的方向表示向量的方向。其中大小相等,方向相同的向量叫做相等向量。
如以正方形的四个顶点中某一点为起点,另一个顶点为终点作向量,可以作出8个不同的向量:、、、、 、、、(由于和是相等向量,因此只算一个)。
⑴ 作两个相邻的正方形(如图一)。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为,试求的值;
⑵ 作个相邻的正方形(如图二)“一字型”排开。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为,试求的值;
…
共n个正方形
⑶ 作个相邻的正方形(如图三)排开。以其中的一个顶点为起点,另一个顶点为终点作向量, 可以作出不同向量的个数记为,试求的值;
图三
⑷ 作个相邻的正方形(如图四)排开。以其中的一个顶点为起点,另一个顶点为终点作向量, 可以作出不同向量的个数记为,试求的值。
答案:
1.【答案】2000
2.【答案】100,5050
3.【答案】(1)0 (2)0
4.【答案】
5.【答案】A
6.【答案】A
7.【答案】C
8.【答案】B
9.【答案】B
10.【答案】B
11.【答案】(1)设直线l的函数表达式为y=k x+b.
∵ 直线l与直线y=—2x—1平行,∴ k=—2.
∵ 直线l过点(1,4),∴ —2+b =4,∴ b =6.
∴ 直线l的函数表达式为y=—2x+6.
直线的图象如图.
(2) ∵直线分别与轴、轴交于点、,∴点、的坐标分别为(0,6)、(3,0).
∵∥,∴直线为y=—2x+t.
∴C点的坐标为.
∵ t>0,∴ .
∴C点在x轴的正半轴上.
当C点在B点的左侧时,;
当C点在B点的右侧时, .
∴△的面积关于的函数表达式为
12.【答案】
13.【答案】正确。证明如下:
方法一:设AC,BD交于O,∵AB=AD,BC=DC,AC=AC,
∴△ABC≌△ADE,
∴∠BAC=∠DAC,AB=AD,∴AO⊥BD,
S△ABD=BD·AO,S△BCD=BD·CO,
所以S四边形ABCD= S△ABD+ S△BCD=BD·AO+BD·CO
=BD(AO+CO)=BD·AC;
方法二:∵AB=AD,
∴点A在线段BD的中垂线上。
又∵CB=CD,∴点C与在线段BD的中垂线上,
∴AC所在的直线是线段BD的中垂线,即BD⊥AC;下同方法一。
14.【答案】⑴
⑵
⑶ =34
⑷ =2()+4()
图2
F
E
D
C
B
A
P
G
H
J
I
图1
B
J
I
H
G
D
C
A
P
图4
图3
图3(1)
图4
图3(2)
y
O
图2
Q(5, 5)
P(2, 3)
y
O
图1
1
1
x
x
y
O
1
1
x
A
B
C
4=1+3 9=3+6 16=6+10
…
A
y
O
B
x
1 2 3 4 3 2 1
2 3 4 5 4 3 2
3 4 5 6 5 4 3
4 5 6 7 6 5 4
5 6 7 8 7 6 5
6 7 8 9 8 7 6
7 8 9 10 9 8 7
2
4
6
2
4
6
-2
-2
AD
BAD
EBAD
CFEBAD
DQFEBAD
图1
AD
BAD
CFEBAD
DQFEBAD
图2
A
B
C
D
O
图一
图二
共
m
个正方形相连
2
4
6
2
4
6
-2
-2
【备考点睛】
新概念型是近几年中考的热点问题,试题的特点在学生已学数学知识的基础上,对旧知识进行重新包装,给出一个“新概念”,然后要求学生学习和运用这个“新概念”来解决相应的数学问题,这类试题对培养学生的阅读理解能力和独立获取新知识、解决新问题的能力有非常重要的作用.面对一个新概念,阅读时至关重要的是用自己的语言来理解它,并把它与熟悉的相关数学知识相挂靠,把一个全新的问题化为熟悉的问题去处理.这类试题能很好地考查学生的数学阅读理解能力、数学抽象概括能力和对“新概念”的实际应用能力。
【经典例题】
例题1。 定义:到凸四边形一组对边距离相等,到另一组对边距离也相等的点叫凸四边形的准内点.如图1,PH=PJ,PI=PG,则点P就是四边形ABCD的准内点.
(1)如图2, 与的角平分线相交于点.求证:点是四边形的准内点.
(2)分别画出图3平行四边形和图4梯形的准内点.(作图工具不限,不写作法,但要有必要的说明)
(3)判断下列命题的真假,在括号内填“真”或“假”.
①任意凸四边形一定存在准内点.( )
②任意凸四边形一定只有一个准内点.( )
③若是任意凸四边形的准内点,则PA+PB=PC+PD或PA+PC=PB+PD.( )
解答:解析:在理解新新概念——准内点的同时,结合已学角的平分线的性质与判定——角平分线上的点到角的两边的距离相等,到角的两边的距离相等的点在这个角的平分线上。当两组对边不平行时,如图1中的点P是直线AD与BC的夹角平分线、直线AB与DC的夹角平分线的交点,当两组对边平行时利用全等三角形等方法构造。
详解:(1)如图2,过点作
,
∵平分, ∴.
同理 .
∴是四边形的准内点.
(2)
平行四边形对角线AC、BD的交点就是准内点,如图3(1).或者取平行四边形两对边中点连线的交点就是准内点,如图3(2);梯形两腰夹角的平分线与梯形中位线的交点就是准内点.如图4.
(3)真;真;假.
例题2。 (2010湖南益阳)我们把对称中心重合,四边分别平行的两个正方形之间的部分叫“方形环”,易知方形环四周的宽度相等.
一条直线l与方形环的边线有四个交点、、、.小明在探究线段与 的数量关系时,从点、向对边作垂线段、,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题:
⑴当直线l与方形环的对边相交时(如图1),直线l分别交、、、于、、、,小明发现与相等,请你帮他说明理由;
⑵当直线l与方形环的邻边相交时(如图2),l分别交、、、于、、、,l与的夹角为,你认为与还相等吗?若相等,说明理由;若不相等,求出的值(用含的三角函数表示).
解答:⑴解: 在方形环中,
∵∥
∴
∴△≌△
∴
⑵解法一:∵
∴∽
∴
∵
∴ (或)
①当时,tan=1,则
②当时,
则 (或)
解法二:在方形环中,
又∵
∴∥
∴
在与中,
HYPERLINK "http://www./"
即 (或)
①当时,
②当时,
则 (或)
例题3。 阅读材料:
如图1-1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法:,即三角形面积等于水平宽与铅垂高乘积的一半.
解答下列问题:
如图1-2,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.
(1)求抛物线和直线AB的解析式;
(2)点P是抛物线(在第一象限内)上的一个动点,连结PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及;
(3)是否存在一点P,使S△PAB=S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
解答:解析:(1)材料中给出了一个基本图形和计算三角形面积的新方法,在解决问题中一定要运用新方法,切不可只用教材中的计算方法,否则问题就很难求解。(2)理解材料是解决问题的关键,在运用公式时注意结合图形理解水平宽与铅垂高的含义,能指出△CAB的铅垂高为CD与水平宽为OA,△PAB的水平宽仍为OA,铅垂高为点P的纵坐标与点B的纵坐标的差。
详解:(1)设抛物线的解析式为:,把A(3,0)代入解析式求得
所以
设直线AB的解析式为:
由求得B点的坐标为
把,代入中
解得:
所以
(2)因为C点坐标为(1,4)
所以当x=1时,y1=4,y2=2
所以CD=4-2=2
(平方单位)
(3)假设存在符合条件的点P,设P点的横坐标为x,△PAB的铅垂高为h,则 HYPERLINK "http:///" 由S△PAB=S△CAB得:
化简得:解得,
将代入中,
解得P点坐标为。
点评:在坐标系中求几何量,注意点的横、纵坐标与线段长度的关联。
例题4。 (2010 浙江台州)类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为 3+()=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为.
解决问题:(1)计算:{3,1}+{1,2};{1,2}+{3,1}.
(2)①动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”
{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”
{3,1}平移,最后的位置还是点B吗 在图1中画出四边形OABC.
②证明四边形OABC是平行四边形.
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程.
解答:(1){3,1}+{1,2}={4,3}.
{1,2}+{3,1}={4,3}.
(2)①画图分
最后的位置仍是B.
② 证明:由①知,A(3,1),B(4,3),C(1,2)
∴OC=AB==,OA=BC==,
∴四边形OABC是平行四边形.
(3){2,3}+{3,2}+{-5,-5}={0, 0}.
例题5。古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”而把1、4、9、16 … 这样的数称为“正方形数”.从图7中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )
A.13 = 3+10 B.25 = 9+16 C.36 = 15+21 D.49 = 18+31
解答:解析:首先要通过图形理解“三角形数”和“正方形数”的概念,进而可以根据两个概念进行排除,像A中的13就不是“正方形数”,B、D中的9、16、18、31都不是“三角形数”,只有C符合条件。
答案:C
点评:对于找规律的题目主要是找出按照什么规律变化的.考查学生的观察、分析、比较、概括的能力和发散思维的能力.
例题6。(2010浙江绍兴)在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,
叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.
(1)求函数y=x+3的坐标三角形的三条边长;
(2)若函数y=x+b(b为常数)的坐标三角形
周长为16, 求此三角形面积.
解答:(1) ∵ 直线y=x+3与x轴的交点坐标为(4,0),与y轴交点坐标为(0,3),
∴函数y=x+3的坐标三角形的三条边长分别为3,4,5.
(2) 直线y=x+b与x轴的交点坐标为(,0),与y轴交点坐标为(0,b),
当b>0时,,得b =4,此时,坐标三角形面积为;
当b<0时,,得b =-4,此时,坐标三角形面积为.
综上,当函数y=x+b的坐标三角形周长为16时,面积为.
例题7。对于任意的两个实数对和,规定:当时,有;运算“”为:;运算“”为:.设、都是实数,若,则
解答:因为,所以p=2,2q=-4,
所以p=2,q=-2.所以(1+p,2+q)=
【技巧提炼】
解决新概念型问题的关键是把握“新概念”的实质,正确理解“新概念”的内涵。首先仔细阅读对于“新概念”的定义;然后运用“新概念”的知识解决新问题.因此,要掌握好初中数学的基础知识,更要注重提高阅读理解、知识迁移、分析转化、探索归纳等多方面的素质,其实,解决问题的思想方法还是通常学到的方法,所以,只要认真思考,还是可以解决的。
【体验中考】
1.(2010安徽蚌埠)若表示不超过的最大整数(如等),则
_________________。
2.(2010广西南宁)古希腊数学家把数叫做三角数,它有一定的规律性.若把一个三角形数记为,第二个三角形数记为,第个三角形数记为,计算, ,由此推算, , .
3.(2010湖南常德)如图,一个数表有7行7列,设表示第i行第j列上的数(其中i=1,2,3,…,7,j=1,2,3,…,7). 例如:第5行第3列上的数.
则(1)= ;
(2)此数表中的四个数满足= .
4.(2010 重庆江津)我们定义,例如=2×5-3×4=10-12=-2.若、均为整数,且满足1<<3,则的值是_________.
5.(2010四川达州)在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换:
①,如;② ,如.
按照以上变换有:,那么等于
A.(3,2) B.(3,-2)
C.(-3,2) D.(-3,-2)
6.(2010浙江宁波)《几何原本》的诞生,标志着几何学已成为一个有着严密理论系统和科学方法的学科,它 奠定了现代数学的基础. 它是下列哪位数学家的著作
(A)欧几里得 (B)杨辉 (C)笛卡尔 (D)刘徽
7.(2010安徽蚌埠)记=,令,称为,,……,这列数的“理想数”。已知,,……,的“理想数”为2004,那么8,,,……,的“理想数”为
A.2004 B.2006 C.2008 D.2010
8.(2010鄂尔多斯)定义新运算: a b=,则函数y=3 x的图象大致是
9.(2010浙江杭州)定义[]为函数的特征数, 下面给出特征数为 [2m,1 – m , –1– m] 的函数的一些结论:
① 当m = – 3时,函数图象的顶点坐标是(,);
② 当m > 0时,函数图象截x轴所得的线段长度大于;
③ 当m < 0时,函数在x >时,y随x的增大而减小;
④ 当m 0时,函数图象经过同一个点.
其中正确的结论有
A. ①②③④ B. ①②④ C. ①③④ D. ②④
10.(2010 山东东营)把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换.在自然界和日常生活中,大量地存在这种图形变换(如图甲).结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,两个对应三角形(如图乙)的对应点所具有的性质是( )
(A)对应点连线与对称轴垂直 (B)对应点连线被对称轴平分
(C)对应点连线被对称轴垂直平分 (D)对应点连线互相平行
11.阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数的图象为直线,一次函数的图象为直线,若,且,我们就称直线与直线互相平行. 解答下面的问题:
(1)求过点且与已知直线平行的直线的函数表达式,并画出直线 的图象;
(2)设直线分别与轴、轴交于点、,如果直线:与直线平行且交轴于点,求出△的面积关于的函数表达式.
12.(2010 江苏连云港) 如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.如,平行四边形的一条对线所在的直线就是平行四边形的一条面积等分线.
(1)三角形的中线、高线、角平分线分别所在的直线一定是三角形的面积等分线的有________;
(2)如图1,梯形ABCD中,AB∥DC,如果延长DC到E,使CE=AB,连接AE,那么有S梯形ABCD=S△ABE.请你给出这个结论成立的理由,并过点A作出梯形ABCD的面积等分线(不写作法,保留作图痕迹);
(3)如图,四边形ABCD中,AB与CD不平行,S△ADC>S△ABC,过点A能否作出四边形ABCD的面积等分线?若能,请画出面积等分线,并给出证明;若不能,说明理由.
13.如图,四边形ABCD中,AB=AD,CB=CD,但AD CD,我们称这样的四边形为“半菱形”。小明说“‘半菱形’的面积等于两条对角线乘积的一半”。他的说法正确吗?请你判断并证明你的结论。
14.(2010安徽蚌埠)定义:在平面内,我们把既有大小又有方向的量叫做平面向量。平面向量可以用有向线段表示,有向线段的长度表示向量的大小,有向线段的方向表示向量的方向。其中大小相等,方向相同的向量叫做相等向量。
如以正方形的四个顶点中某一点为起点,另一个顶点为终点作向量,可以作出8个不同的向量:、、、、 、、、(由于和是相等向量,因此只算一个)。
⑴ 作两个相邻的正方形(如图一)。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为,试求的值;
⑵ 作个相邻的正方形(如图二)“一字型”排开。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为,试求的值;
…
共n个正方形
⑶ 作个相邻的正方形(如图三)排开。以其中的一个顶点为起点,另一个顶点为终点作向量, 可以作出不同向量的个数记为,试求的值;
图三
⑷ 作个相邻的正方形(如图四)排开。以其中的一个顶点为起点,另一个顶点为终点作向量, 可以作出不同向量的个数记为,试求的值。
答案:
1.【答案】2000
2.【答案】100,5050
3.【答案】(1)0 (2)0
4.【答案】
5.【答案】A
6.【答案】A
7.【答案】C
8.【答案】B
9.【答案】B
10.【答案】B
11.【答案】(1)设直线l的函数表达式为y=k x+b.
∵ 直线l与直线y=—2x—1平行,∴ k=—2.
∵ 直线l过点(1,4),∴ —2+b =4,∴ b =6.
∴ 直线l的函数表达式为y=—2x+6.
直线的图象如图.
(2) ∵直线分别与轴、轴交于点、,∴点、的坐标分别为(0,6)、(3,0).
∵∥,∴直线为y=—2x+t.
∴C点的坐标为.
∵ t>0,∴ .
∴C点在x轴的正半轴上.
当C点在B点的左侧时,;
当C点在B点的右侧时, .
∴△的面积关于的函数表达式为
12.【答案】
13.【答案】正确。证明如下:
方法一:设AC,BD交于O,∵AB=AD,BC=DC,AC=AC,
∴△ABC≌△ADE,
∴∠BAC=∠DAC,AB=AD,∴AO⊥BD,
S△ABD=BD·AO,S△BCD=BD·CO,
所以S四边形ABCD= S△ABD+ S△BCD=BD·AO+BD·CO
=BD(AO+CO)=BD·AC;
方法二:∵AB=AD,
∴点A在线段BD的中垂线上。
又∵CB=CD,∴点C与在线段BD的中垂线上,
∴AC所在的直线是线段BD的中垂线,即BD⊥AC;下同方法一。
14.【答案】⑴
⑵
⑶ =34
⑷ =2()+4()
图2
F
E
D
C
B
A
P
G
H
J
I
图1
B
J
I
H
G
D
C
A
P
图4
图3
图3(1)
图4
图3(2)
y
O
图2
Q(5, 5)
P(2, 3)
y
O
图1
1
1
x
x
y
O
1
1
x
A
B
C
4=1+3 9=3+6 16=6+10
…
A
y
O
B
x
1 2 3 4 3 2 1
2 3 4 5 4 3 2
3 4 5 6 5 4 3
4 5 6 7 6 5 4
5 6 7 8 7 6 5
6 7 8 9 8 7 6
7 8 9 10 9 8 7
2
4
6
2
4
6
-2
-2
AD
BAD
EBAD
CFEBAD
DQFEBAD
图1
AD
BAD
CFEBAD
DQFEBAD
图2
A
B
C
D
O
图一
图二
共
m
个正方形相连
2
4
6
2
4
6
-2
-2
同课章节目录
