高二数学(理)人教版期末复习学案 空间中的垂直与空间角 Word版含解析
文档属性
| 名称 | 高二数学(理)人教版期末复习学案 空间中的垂直与空间角 Word版含解析 |

|
|
| 格式 | docx | ||
| 文件大小 | 350.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 22:13:18 | ||
图片预览




文档简介
空间中的垂直与空间角
题型一 证明垂直关系求线面角
【例1】(2019浙江,19)如图,已知三棱柱ABC-A1B1C1,平面A1ACC1⊥平面ABC,∠ABC=90°,∠BAC=30°,A1A=A1C=AC,E,F分别是AC,A1B1的中点.
(1)证明:EF⊥BC;
(2)求直线EF与平面A1BC所成角的余弦值.
解题心得求线面角可以用几何法,即“先找,后证,再求”,也可以通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角,取其余角就是斜线和平面所成的角.
对点训练1(2020新高考全国1,20)
如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.
(1)证明:l⊥平面PDC;
(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.
题型二 证垂直关系及求二面角
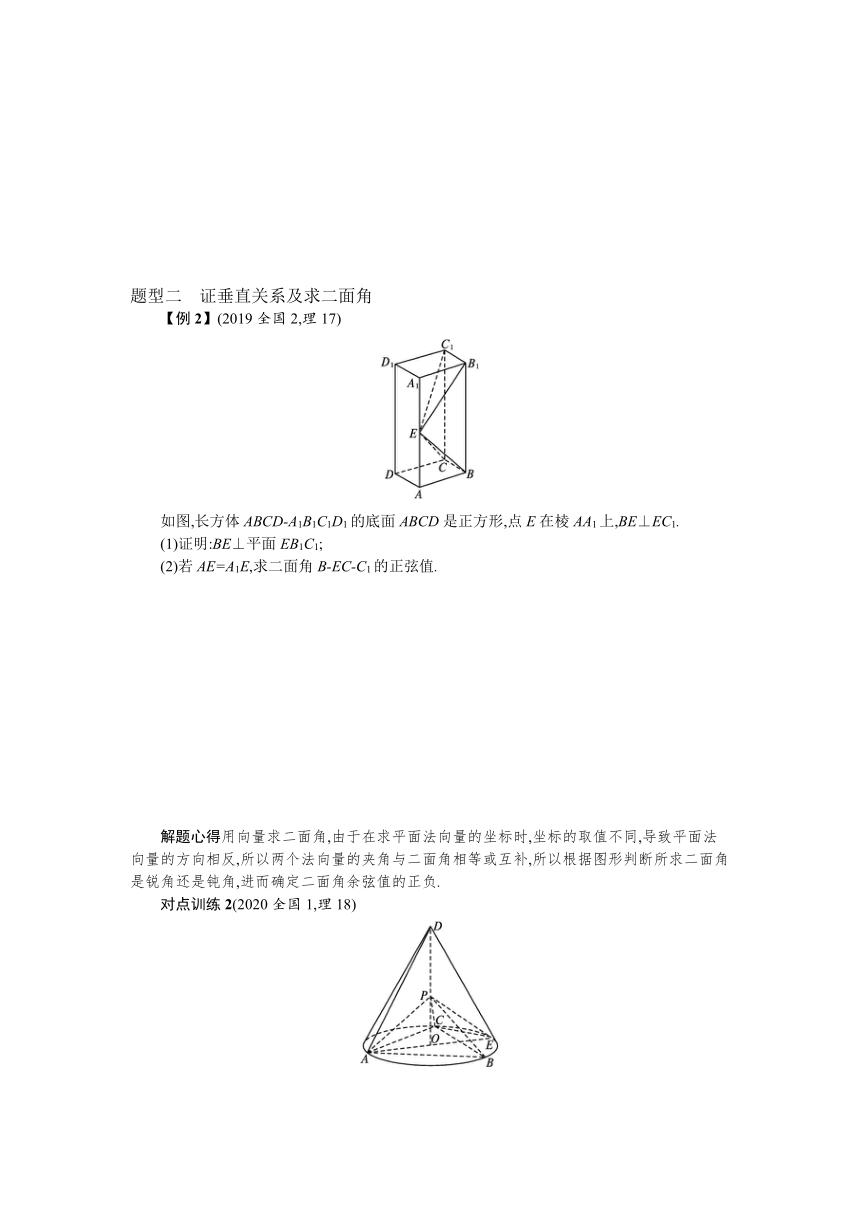
【例2】(2019全国2,理17)
如图,长方体ABCD-A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,求二面角B-EC-C1的正弦值.
解题心得用向量求二面角,由于在求平面法向量的坐标时,坐标的取值不同,导致平面法向量的方向相反,所以两个法向量的夹角与二面角相等或互补,所以根据图形判断所求二面角是锐角还是钝角,进而确定二面角余弦值的正负.
对点训练2(2020全国1,理18)
如图,D为圆锥的顶点,O是圆锥底面的圆心,AE为底面直径,AE=AD.△ABC是底面的内接正三角形,P为DO上一点,PO=66DO.
(1)证明:PA⊥平面PBC;
(2)求二面角B-PC-E的余弦值.
题型三 求空间角与存在垂直关系问题
【例3】如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PCD⊥平面ABCD,AB=2,BC=1,PC=PD=2,E为PB中点.
(1)求证:PD∥平面ACE;
(2)求二面角E-AC-D的余弦值;
(3)在棱PD上是否存在点M,使得AM⊥BD?若存在,求PMPD的值;若不存在,说明理由.
解题心得线面垂直中的探索性问题同“平行关系中的探索性问题”的规律方法一样,有两种解法,一是几何法,先探求点的位置,多为线段的中点或某个三等分点,然后给出符合要求的证明.二是利用空间向量探索,把要成立的结论当作条件,据此列方程或方程组,通过坐标运算进行判断.
对点训练3如图1,在边长为2的菱形ABCD中,∠BAD=60°,将△BCD沿对角线BD折起到△BC'D的位置,使平面BC'D⊥平面ABD,E是BD的中点,FA⊥平面ABD,且FA=23,如图2.
(1)求证:FA∥平面BC'D;
(2)求平面ABD与平面FBC'所成角的余弦值;
(3)在线段AD上是否存在一点M,使得C'M⊥平面FBC'?若存在,求AMAD的值;若不存在,说明理由.
题型四 求空间点到面的距离
【例4】如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF的中点.
(1)求M到平面DEC的距离及三棱锥M-CDE的体积;
(2)求证:DM⊥平面ACE.
解题心得求空间的距离用找公垂线的方法比较难下手,用向量代数的方法则简捷,高效.
(1)点P到平面α的距离可以通过在平面α内任取一点A,求向量PA在平面α的法向量n上的投影来解决.即若PA为平面α的一条斜线段,n为平面α的法向量,则B到平面α的距离d=|PA·n||n|.
(2)异面直线间的距离可以通过在两条直线上任意各取一点A,B,求向量AB在公垂线的方向向量n上的投影来解决;直线到与其平行的平面的距离,平行平面间的距离都可转化为点到平面的距离.
对点训练4底面为菱形的直棱柱ABCD-A1B1C1D1中,E、F分别为棱A1B1、A1D1的中点,
(1)在图中作一个平面α,使得BD?α,且平面AEF∥α(不必给出证明过程,只要求作出α与直棱柱ABCD-A1B1C1D1的截面);
(2)若AB=AA1=2,∠BAD=60°,求点C到所作截面α的距离.
2 空间中的垂直与空间角
例1方法一:
(1)证明连接A1E,因为A1A=A1C,E是AC的中点,
所以A1E⊥AC.又平面A1ACC1⊥平面ABC,A1E?平面A1ACC1,
平面A1ACC1∩平面ABC=AC,
所以,A1E⊥平面ABC,则A1E⊥BC.
又因为A1F∥AB,∠ABC=90°,
故BC⊥A1F.所以BC⊥平面A1EF.
因此EF⊥BC.
(2)解取BC中点G,连接EG,GF,则EGFA1是平行四边形.由于A1E⊥平面ABC,故A1E⊥EG,所以平行四边形EGFA1为矩形.
由(1)得BC⊥平面EGFA1,则平面A1BC⊥平面EGFA1,所以EF在平面A1BC上的射影在直线A1G上.
连接A1G交EF于O,则∠EOG是直线EF与平面A1BC所成的角(或其补角).
不妨设AC=4,则在Rt△A1EG中,A1E=23,EG=3.由于O为A1G的中点,故EO=OG=A1G2=152,
所以cos∠EOG=EO2+OG2-EG22EO·OG=35.
因此,直线EF与平面A1BC所成角的余弦值是35.
方法二:
(1)证明连接A1E,因为A1A=A1C,E是AC的中点,所以A1E⊥AC.
又平面A1ACC1⊥平面ABC,A1E?平面A1ACC1,平面A1ACC1∩平面ABC=AC,所以,A1E⊥平面ABC.
如图,以点E为原点,分别以射线EC,EA1为y,z轴的正半轴,建立空间直角坐标系E-xyz.
不妨设AC=4,则A1(0,0,23),B(3,1,0),B1(3,3,23),F32,32,23,C(0,2,0).
因此,EF=32,32,23,BC=(-3,1,0).由EF·BC=0得EF⊥BC.
(2)解设直线EF与平面A1BC所成角为θ.
由(1)可得BC=(-3,1,0),A1C=(0.2,-23).
设平面A1BC的一个法向量为n=(x,y,z).由BC·n=0,A1C·n=0,得-3x+y=0,y-3z=0.
取n=(1,3,1),故sinθ=|cos|=|EF·n||EF|·|n|=45.因此,直线EF与平面A1BC所成的角的余弦值为35.
对点训练1解(1)因为PD⊥底面ABCD,所以PD⊥AD.
又底面ABCD为正方形,所以AD⊥DC.所以AD⊥平面PDC.
因为AD∥BC,AD不在平面PBC中,所以AD∥平面PBC,又因为AD?平面PAD,平面PAD∩平面PBC=l,所以l∥AD.所以l⊥平面PDC.
(2)以D为坐标原点,分别以DA,DC,DP的方向为x轴,y轴,z轴的正方向,建立如图所示的空间直角坐标系D-xyz.
由PD=AD=1,得D(0,0,0),C(0,1,0),B(1,1,0),P(0,0,1),则DC=(0,1,0),PB=(1,1,-1).
由(1)可设Q(a,0,1),则DQ=(a,0,1).设n=(x,y,z)是平面QCD的法向量,
则n·DQ=0,n·DC=0,即ax+z=0,y=0.可取n=(-1,0,a).所以cos=n·PB|n||PB| =-1-a31+a2.
设PB与平面QCD所成角为θ,则sinθ=33×|a+1|1+a2=331+2aa2+1.
因为331+2aa2+1≤63,当且仅当a=1时,等号成立,所以PB与平面QCD所成角的正弦值的最大值为63.
例2
(1)证明由已知得,B1C1⊥平面ABB1A1,BE?平面ABB1A1,故B1C1⊥BE.又BE⊥EC1,所以BE⊥平面EB1C1.
(2)解由(1)知∠BEB1=90°.由题设知Rt△ABE≌Rt△A1B1E,所以∠AEB=45°,故AE=AB,AA1=2AB.
以D为坐标原点,DA的方向为x轴正方向,|DA|为单位长,建立如图所示的空间直角坐标系D-xyz,则C(0,1,0),B(1,1,0),C1(0,1,2),E(1,0,1),CB=(1,0,0),CE=(1,-1,1),CC1=(0,0,2).
设平面EBC的一个法向量为n=(x,y,z),则CB·n=0,CE·n=0,即x=0,x-y+z=0,
所以可取n=(0,-1,-1).
设平面ECC1的一个法向量为m=(x,y,z),则
CC1·m=0,CE·m=0,即2z=0,x-y+z=0,
所以可取m=(1,1,0).
于是cos=n·m|n||m|=-12.
所以,二面角B-EC-C1的正弦值为32.
对点训练2(1)证明设DO=a,由题设可得PO=66a,AO=33a,AB=a,PA=PB=PC=22a.因此PA2+PB2=AB2,从而PA⊥PB.
又PA2+PC2=AC2,故PA⊥PC.
所以PA⊥平面PBC.
(2)解以O为坐标原点,OE的方向为y轴正方向,|OE|为单位长,建立如图所示的空间直角坐标系O-xyz.由题设可得E(0,1,0),A(0,-1,0),C-32,12,0,P0,0,22.所以EC=-32,-12,0,EP=0,-1,22.设m=(x,y,z)是平面PCE的法向量,
则m·EP=0,m·EC=0,即-y+22z=0,-32x-12y=0.
可取m=-33,1,2.
由(1)知AP=0,1,22是平面PCB的一个法向量,记n=AP,
则cos=n·m|n|·|m|=255.所以二面角B-PC-E的余弦值为255.
例3(1)证明设BD交AC于点F,连接EF.因为底面ABCD是矩形,所以F为BD中点.又因为E为PB中点,所以EF∥PD.
因为PD?平面ACE,EF?平面ACE,所以PD∥平面ACE.
(2)解取CD的中点O,连接PO,FO.因为底面ABCD为矩形,所以BC⊥CD.
因为PC=PD,O为CD中点,所以PO⊥CD,OF∥BC,所以OF⊥CD.
又因为平面PCD⊥平面ABCD,PO?平面PCD,平面PCD∩平面ABCD=CD,所以PO⊥平面ABCD.
如图,建立空间直角坐标系O-xyz,则A(1,-1,0),C(0,1,0),B(1,1,0),P(0,0,1),E12,12,12,
设平面ACE的一个法向量为m=(x,y,z),AC=(-1,2,0),AE=-12,32,12,所以AC·m=0,AE·m=0?-x+2y=0,-12x+32y+12z=0?x=2y,z=-y.
令y=1,则x=2,z=-1,所以m=(2,1,-1).
平面ACD的法向量为OP=(0,0,1),则cos=m·OP|m|·|OP|=-66.
如图可知二面角E-AC-D为钝角,所以二面角E-AC-D的余弦值为-66.
(3)在棱PD上存在点M,使AM⊥BD.设PMPD=λ(λ∈[0,1]),M(x,y,z),PM=λPD,D(0,-1,0).
因为(x,y,z-1)=λ(0,-1,-1),所以M(0,-λ,1-λ).AM=(-1,1-λ,1-λ),BD=(-1,-2,0).
因为AM⊥BD,所以AM·BD=0.所以1-2(1-λ)=0,解得λ=12∈[0,1].
所以在棱PD上存在点M,使AM⊥BD,且PMPD=12.
对点训练3(1)证明∵BC=CD,E为BD的中点,∴C'E⊥BD.
又平面BC'D⊥平面ABD,且平面BC'D∩平面ABD=BD,
∴C'E⊥平面ABD.
∵FA⊥平面ABD,∴FA∥C'E.而C'E?平面BC'D,FA?平面BC'D,
∴FA∥平面BC'D.
(2)解以DB所在直线为x轴,AE所在直线为y轴,EC'所在直线为z轴建立空间直角坐标系,
则B(1,0,0),A(0,-3,0),D(-1,0,0),F(0,-3,23),C'(0,0,3),
∴BF=(-1,-3,23),BC'=(-1,0,3).设平面FBC'的一个法向量为m=(x,y,z),
则m·BF=-x-3y+23z=0,m·BC'=-x+3z=0,
取z=1,则m=(3,1,1).
又平面ABD的一个法向量为n=(0,0,1),∴cos=m·n|m||n|=15·1=55.
则平面ABD与平面FBC'所成角的余弦值为55.
(3)解假设在线段AD上存在M(x,y,z),使得C'M⊥平面FBC',
设AM=λAD,则(x,y+3,z)=λ(-1,3,0)=(-λ,3λ,0),
∴x=-λ,y=3(λ-1),z=0.
而C'M=(-λ,3(λ-1),-3).
由m·C'M=0,得-3λ+3(λ-1)-3=0,即-23=0错误.
∴线段AD上不存点M,使得C'M⊥平面FBC.
例4(1)解设AC∩BD=O,以O为原点,OB为x轴,OC为y轴,
过O作平面ABCD的垂线为z轴,建立空间直角坐标系,
则C(0,3,0),D(-1,0,0),E(-1,0,2),M(1,0,1),
DE=(0,0,2),DC=(1,3,0),DM=(2,0,1),∵DE·DC=0,∴DE⊥DC,
∴S△DEC=12×DE×DC=12×2×2=2.设平面DEC的法向量n=(x,y,z),
则n·DE=2z=0,n·DC=x+3y=0,取x=3,得n=(3,-1,0),∴M到平面DEC的距离h=|DM·n||n|=233+1=3.
∴三棱锥M-CDE的体积:V=13×S△CDE×h=13×2×3=233.
(2)证明A(0,-3,0),AC=(0,23,0),AE=(-1,3,2),
AC·DM=0,AE·DM=-2+2=0,
∴AC⊥DM,AE⊥DM,
∵AC∩AE=A,∴DM⊥平面ACE.
对点训练4解(1)取B1C1的中点G,D1C1的中点H,连接BG,GH,DH.
则平面BDHG就是所求的平面α,α与直棱柱ABCD-A1B1C1D1的截面即为平面BDHG.
(2)取BC中点M,∵AB=AA1=2,∠BAD=60°,∴以D为原点,DA为x轴,DM为y轴,DD1为z轴建立空间直角坐标系,则C(-1,3,0),D(0,0,0),B(1,3,0),G(0,3,2),
DB=(1,3,0),DG=(0,3,2),DC=(-1,3,0),
设平面BDG的法向量n=(x,y,z),
则n·DB=x+3y=0,n·DG=3y+2z=0,取y=1,得n=(23,-2,3),
∴点C到所作截面α的距离d=|n·DC||n|=43219=25719.
题型一 证明垂直关系求线面角
【例1】(2019浙江,19)如图,已知三棱柱ABC-A1B1C1,平面A1ACC1⊥平面ABC,∠ABC=90°,∠BAC=30°,A1A=A1C=AC,E,F分别是AC,A1B1的中点.
(1)证明:EF⊥BC;
(2)求直线EF与平面A1BC所成角的余弦值.
解题心得求线面角可以用几何法,即“先找,后证,再求”,也可以通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角,取其余角就是斜线和平面所成的角.
对点训练1(2020新高考全国1,20)
如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.
(1)证明:l⊥平面PDC;
(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.
题型二 证垂直关系及求二面角
【例2】(2019全国2,理17)
如图,长方体ABCD-A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,求二面角B-EC-C1的正弦值.
解题心得用向量求二面角,由于在求平面法向量的坐标时,坐标的取值不同,导致平面法向量的方向相反,所以两个法向量的夹角与二面角相等或互补,所以根据图形判断所求二面角是锐角还是钝角,进而确定二面角余弦值的正负.
对点训练2(2020全国1,理18)
如图,D为圆锥的顶点,O是圆锥底面的圆心,AE为底面直径,AE=AD.△ABC是底面的内接正三角形,P为DO上一点,PO=66DO.
(1)证明:PA⊥平面PBC;
(2)求二面角B-PC-E的余弦值.
题型三 求空间角与存在垂直关系问题
【例3】如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PCD⊥平面ABCD,AB=2,BC=1,PC=PD=2,E为PB中点.
(1)求证:PD∥平面ACE;
(2)求二面角E-AC-D的余弦值;
(3)在棱PD上是否存在点M,使得AM⊥BD?若存在,求PMPD的值;若不存在,说明理由.
解题心得线面垂直中的探索性问题同“平行关系中的探索性问题”的规律方法一样,有两种解法,一是几何法,先探求点的位置,多为线段的中点或某个三等分点,然后给出符合要求的证明.二是利用空间向量探索,把要成立的结论当作条件,据此列方程或方程组,通过坐标运算进行判断.
对点训练3如图1,在边长为2的菱形ABCD中,∠BAD=60°,将△BCD沿对角线BD折起到△BC'D的位置,使平面BC'D⊥平面ABD,E是BD的中点,FA⊥平面ABD,且FA=23,如图2.
(1)求证:FA∥平面BC'D;
(2)求平面ABD与平面FBC'所成角的余弦值;
(3)在线段AD上是否存在一点M,使得C'M⊥平面FBC'?若存在,求AMAD的值;若不存在,说明理由.
题型四 求空间点到面的距离
【例4】如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF的中点.
(1)求M到平面DEC的距离及三棱锥M-CDE的体积;
(2)求证:DM⊥平面ACE.
解题心得求空间的距离用找公垂线的方法比较难下手,用向量代数的方法则简捷,高效.
(1)点P到平面α的距离可以通过在平面α内任取一点A,求向量PA在平面α的法向量n上的投影来解决.即若PA为平面α的一条斜线段,n为平面α的法向量,则B到平面α的距离d=|PA·n||n|.
(2)异面直线间的距离可以通过在两条直线上任意各取一点A,B,求向量AB在公垂线的方向向量n上的投影来解决;直线到与其平行的平面的距离,平行平面间的距离都可转化为点到平面的距离.
对点训练4底面为菱形的直棱柱ABCD-A1B1C1D1中,E、F分别为棱A1B1、A1D1的中点,
(1)在图中作一个平面α,使得BD?α,且平面AEF∥α(不必给出证明过程,只要求作出α与直棱柱ABCD-A1B1C1D1的截面);
(2)若AB=AA1=2,∠BAD=60°,求点C到所作截面α的距离.
2 空间中的垂直与空间角
例1方法一:
(1)证明连接A1E,因为A1A=A1C,E是AC的中点,
所以A1E⊥AC.又平面A1ACC1⊥平面ABC,A1E?平面A1ACC1,
平面A1ACC1∩平面ABC=AC,
所以,A1E⊥平面ABC,则A1E⊥BC.
又因为A1F∥AB,∠ABC=90°,
故BC⊥A1F.所以BC⊥平面A1EF.
因此EF⊥BC.
(2)解取BC中点G,连接EG,GF,则EGFA1是平行四边形.由于A1E⊥平面ABC,故A1E⊥EG,所以平行四边形EGFA1为矩形.
由(1)得BC⊥平面EGFA1,则平面A1BC⊥平面EGFA1,所以EF在平面A1BC上的射影在直线A1G上.
连接A1G交EF于O,则∠EOG是直线EF与平面A1BC所成的角(或其补角).
不妨设AC=4,则在Rt△A1EG中,A1E=23,EG=3.由于O为A1G的中点,故EO=OG=A1G2=152,
所以cos∠EOG=EO2+OG2-EG22EO·OG=35.
因此,直线EF与平面A1BC所成角的余弦值是35.
方法二:
(1)证明连接A1E,因为A1A=A1C,E是AC的中点,所以A1E⊥AC.
又平面A1ACC1⊥平面ABC,A1E?平面A1ACC1,平面A1ACC1∩平面ABC=AC,所以,A1E⊥平面ABC.
如图,以点E为原点,分别以射线EC,EA1为y,z轴的正半轴,建立空间直角坐标系E-xyz.
不妨设AC=4,则A1(0,0,23),B(3,1,0),B1(3,3,23),F32,32,23,C(0,2,0).
因此,EF=32,32,23,BC=(-3,1,0).由EF·BC=0得EF⊥BC.
(2)解设直线EF与平面A1BC所成角为θ.
由(1)可得BC=(-3,1,0),A1C=(0.2,-23).
设平面A1BC的一个法向量为n=(x,y,z).由BC·n=0,A1C·n=0,得-3x+y=0,y-3z=0.
取n=(1,3,1),故sinθ=|cos
对点训练1解(1)因为PD⊥底面ABCD,所以PD⊥AD.
又底面ABCD为正方形,所以AD⊥DC.所以AD⊥平面PDC.
因为AD∥BC,AD不在平面PBC中,所以AD∥平面PBC,又因为AD?平面PAD,平面PAD∩平面PBC=l,所以l∥AD.所以l⊥平面PDC.
(2)以D为坐标原点,分别以DA,DC,DP的方向为x轴,y轴,z轴的正方向,建立如图所示的空间直角坐标系D-xyz.
由PD=AD=1,得D(0,0,0),C(0,1,0),B(1,1,0),P(0,0,1),则DC=(0,1,0),PB=(1,1,-1).
由(1)可设Q(a,0,1),则DQ=(a,0,1).设n=(x,y,z)是平面QCD的法向量,
则n·DQ=0,n·DC=0,即ax+z=0,y=0.可取n=(-1,0,a).所以cos
设PB与平面QCD所成角为θ,则sinθ=33×|a+1|1+a2=331+2aa2+1.
因为331+2aa2+1≤63,当且仅当a=1时,等号成立,所以PB与平面QCD所成角的正弦值的最大值为63.
例2
(1)证明由已知得,B1C1⊥平面ABB1A1,BE?平面ABB1A1,故B1C1⊥BE.又BE⊥EC1,所以BE⊥平面EB1C1.
(2)解由(1)知∠BEB1=90°.由题设知Rt△ABE≌Rt△A1B1E,所以∠AEB=45°,故AE=AB,AA1=2AB.
以D为坐标原点,DA的方向为x轴正方向,|DA|为单位长,建立如图所示的空间直角坐标系D-xyz,则C(0,1,0),B(1,1,0),C1(0,1,2),E(1,0,1),CB=(1,0,0),CE=(1,-1,1),CC1=(0,0,2).
设平面EBC的一个法向量为n=(x,y,z),则CB·n=0,CE·n=0,即x=0,x-y+z=0,
所以可取n=(0,-1,-1).
设平面ECC1的一个法向量为m=(x,y,z),则
CC1·m=0,CE·m=0,即2z=0,x-y+z=0,
所以可取m=(1,1,0).
于是cos
所以,二面角B-EC-C1的正弦值为32.
对点训练2(1)证明设DO=a,由题设可得PO=66a,AO=33a,AB=a,PA=PB=PC=22a.因此PA2+PB2=AB2,从而PA⊥PB.
又PA2+PC2=AC2,故PA⊥PC.
所以PA⊥平面PBC.
(2)解以O为坐标原点,OE的方向为y轴正方向,|OE|为单位长,建立如图所示的空间直角坐标系O-xyz.由题设可得E(0,1,0),A(0,-1,0),C-32,12,0,P0,0,22.所以EC=-32,-12,0,EP=0,-1,22.设m=(x,y,z)是平面PCE的法向量,
则m·EP=0,m·EC=0,即-y+22z=0,-32x-12y=0.
可取m=-33,1,2.
由(1)知AP=0,1,22是平面PCB的一个法向量,记n=AP,
则cos
例3(1)证明设BD交AC于点F,连接EF.因为底面ABCD是矩形,所以F为BD中点.又因为E为PB中点,所以EF∥PD.
因为PD?平面ACE,EF?平面ACE,所以PD∥平面ACE.
(2)解取CD的中点O,连接PO,FO.因为底面ABCD为矩形,所以BC⊥CD.
因为PC=PD,O为CD中点,所以PO⊥CD,OF∥BC,所以OF⊥CD.
又因为平面PCD⊥平面ABCD,PO?平面PCD,平面PCD∩平面ABCD=CD,所以PO⊥平面ABCD.
如图,建立空间直角坐标系O-xyz,则A(1,-1,0),C(0,1,0),B(1,1,0),P(0,0,1),E12,12,12,
设平面ACE的一个法向量为m=(x,y,z),AC=(-1,2,0),AE=-12,32,12,所以AC·m=0,AE·m=0?-x+2y=0,-12x+32y+12z=0?x=2y,z=-y.
令y=1,则x=2,z=-1,所以m=(2,1,-1).
平面ACD的法向量为OP=(0,0,1),则cos
如图可知二面角E-AC-D为钝角,所以二面角E-AC-D的余弦值为-66.
(3)在棱PD上存在点M,使AM⊥BD.设PMPD=λ(λ∈[0,1]),M(x,y,z),PM=λPD,D(0,-1,0).
因为(x,y,z-1)=λ(0,-1,-1),所以M(0,-λ,1-λ).AM=(-1,1-λ,1-λ),BD=(-1,-2,0).
因为AM⊥BD,所以AM·BD=0.所以1-2(1-λ)=0,解得λ=12∈[0,1].
所以在棱PD上存在点M,使AM⊥BD,且PMPD=12.
对点训练3(1)证明∵BC=CD,E为BD的中点,∴C'E⊥BD.
又平面BC'D⊥平面ABD,且平面BC'D∩平面ABD=BD,
∴C'E⊥平面ABD.
∵FA⊥平面ABD,∴FA∥C'E.而C'E?平面BC'D,FA?平面BC'D,
∴FA∥平面BC'D.
(2)解以DB所在直线为x轴,AE所在直线为y轴,EC'所在直线为z轴建立空间直角坐标系,
则B(1,0,0),A(0,-3,0),D(-1,0,0),F(0,-3,23),C'(0,0,3),
∴BF=(-1,-3,23),BC'=(-1,0,3).设平面FBC'的一个法向量为m=(x,y,z),
则m·BF=-x-3y+23z=0,m·BC'=-x+3z=0,
取z=1,则m=(3,1,1).
又平面ABD的一个法向量为n=(0,0,1),∴cos
则平面ABD与平面FBC'所成角的余弦值为55.
(3)解假设在线段AD上存在M(x,y,z),使得C'M⊥平面FBC',
设AM=λAD,则(x,y+3,z)=λ(-1,3,0)=(-λ,3λ,0),
∴x=-λ,y=3(λ-1),z=0.
而C'M=(-λ,3(λ-1),-3).
由m·C'M=0,得-3λ+3(λ-1)-3=0,即-23=0错误.
∴线段AD上不存点M,使得C'M⊥平面FBC.
例4(1)解设AC∩BD=O,以O为原点,OB为x轴,OC为y轴,
过O作平面ABCD的垂线为z轴,建立空间直角坐标系,
则C(0,3,0),D(-1,0,0),E(-1,0,2),M(1,0,1),
DE=(0,0,2),DC=(1,3,0),DM=(2,0,1),∵DE·DC=0,∴DE⊥DC,
∴S△DEC=12×DE×DC=12×2×2=2.设平面DEC的法向量n=(x,y,z),
则n·DE=2z=0,n·DC=x+3y=0,取x=3,得n=(3,-1,0),∴M到平面DEC的距离h=|DM·n||n|=233+1=3.
∴三棱锥M-CDE的体积:V=13×S△CDE×h=13×2×3=233.
(2)证明A(0,-3,0),AC=(0,23,0),AE=(-1,3,2),
AC·DM=0,AE·DM=-2+2=0,
∴AC⊥DM,AE⊥DM,
∵AC∩AE=A,∴DM⊥平面ACE.
对点训练4解(1)取B1C1的中点G,D1C1的中点H,连接BG,GH,DH.
则平面BDHG就是所求的平面α,α与直棱柱ABCD-A1B1C1D1的截面即为平面BDHG.
(2)取BC中点M,∵AB=AA1=2,∠BAD=60°,∴以D为原点,DA为x轴,DM为y轴,DD1为z轴建立空间直角坐标系,则C(-1,3,0),D(0,0,0),B(1,3,0),G(0,3,2),
DB=(1,3,0),DG=(0,3,2),DC=(-1,3,0),
设平面BDG的法向量n=(x,y,z),
则n·DB=x+3y=0,n·DG=3y+2z=0,取y=1,得n=(23,-2,3),
∴点C到所作截面α的距离d=|n·DC||n|=43219=25719.
同课章节目录
